基于改进灰色关联模型的航道优化研究*

王艳锋 王梦紫(武汉交通职业学院,湖北 武汉 430065)

基于改进灰色关联模型的航道优化研究*

王艳锋 王梦紫
(武汉交通职业学院,湖北 武汉 430065)

航道是影响船舶安全航行的重要因素。航道设计是否满足船舶通航要求,航道布置是否合理直接关系到船舶的航行安全。文章在对航道通航环境特征了解、分析的基础上,采用改进灰色关联分析法,对航道方案进行综合评价研究,实现对航道优化方案的比选,给出科学、合理的航道优化方案,为航道设计部门的管理与决策提供参考。

灰色关联;航道优化;航道方案评价

为了减少水上交通事故的发生,除了从人和船的角度考虑以外,还应考虑复杂多变的航道水域通航环境对船舶航行安全的影响。航道作为影响船舶安全航行的重要因素,航道设计是否满足船舶通航要求,航道布置是否合理,这一系列问题都直接关系到船舶的航行安全。为了满足航运业未来发展对航道的需求,改善航道通航安全现状,航道设计部门根据航道设计规范及标准[1],结合水域船舶操纵环境的实际情况,设计出多个航道优化方案,对多个航道优化方案的评价和比选成为验证航道合理性和安全性的关键。因此,通过对航道优化方案进行定量的综合评价,选出航道优化的科学方案,对保障船舶在复杂航道水域航行安全具有重要意义。

1 灰色关联分析的评价模型

航道方案评价实质上是对各个指标因子的影响程度评价,应用灰色关联分析法对离散的指标序列之间进行关联性分析,得到方案序列与比较序列的灰色关联度,最终获取方案评价的排序,遴选出最优方案。根据灰色关联理论,可构建出航道综合评价模型[2][3]。

1.1 原始矩阵与理想向量

航道方案的比选问题实质上是对同一水域的多个不同设计方案的决策问题。根据原始矩阵和理想向量的构建方法,航道方案综合评价系统是由n个优化方案和m个评价指标构成的。

以第i个航道方案的m项指标组成集合:

1.2 对矩阵规范化处理

由于对航道评价使用的各指标数列标度类型和纲量具有差异性,为了使各指标能够进行相互比较,计算获取关联系数,需将矩阵内的原始数据利用下列公式进行规范化处理,将评价指标规范到同一纲量。

得出规范化矩阵:

1.3 灰色平均关联系数

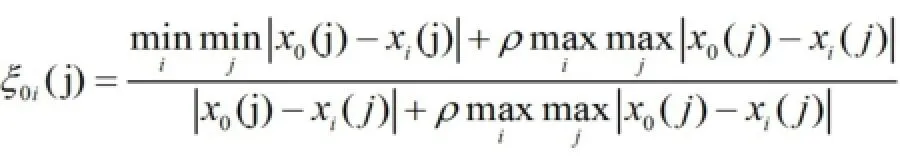
式中:ρ为分辨系数,通常取0.5。

1.4 灰色关联度矩阵

通过以下公式分别计算每个方案中各指标行对于理想序列的灰色关联系数,得灰色关联矩阵:

2 灰色关联分析指标权重

2.1 AHP确定权重

根据构建的评价指标体系,利用层次分析法来判断矩阵的确定方法。本文制定了航道方案评价指标权重调查表,通过专家对评价指标的主观评判,构造评价指标的相对重要度的判断矩阵,并应用层次分析法对判断矩阵进行计算和一致性检验,得到指标的权重向量α＝(α1,α2,α3,···,αj, ···,αn)。

2.2 熵值法确定权重

根据熵值法确定权重的计算步骤,首先应用航道方案的原始数据构造判断矩阵并对其标准化处理,得到归一化矩阵;其次,利用熵值法获取各评价指标的熵值和差异系数,得到评价指标权重向量β＝(β1,β2,···,βj,···,βn)。

2.3 组合赋权

为了保障指标权重确定的真实性和准确性,采用组合赋权法对评价指标进行赋权。这样既能根据原始数据进行客观计算,又能兼顾专家的经验进行主观评判。

具体的赋权公式为:

其中,αj为AHP法确定的第j个指标的权重; βj为熵值法确定的第j个评价指标的权重。

3 改进型灰色关联评价模型

根据对传统灰色关联度计算模型的研究结果表明,传统灰色关联度的获取缺乏对指标因子权重的考虑。由于各指标因子在系统评价中的影响程度存在差异性,若不能正确地反映指标的影响,将会导致评价结果不能真实反映实际情况。为了克服以上缺陷,本文所建的评价模型着重对不同指标的贡献度进行了分析,利用组合赋权法对评价指标进行权重赋值,对传统灰色关联分析模型进行改进,使备选方案与理想方案的关联度更能反映评价的真实性,科学地优选出最佳的航道方案。

其中:ξ0i(j)为灰色关联系数;ω(j)为各指标的综合权重值。本文将以坭洲航道方案评价为例,针对航道评价的特性,应用上述评价模型对实际方案序列和理想序列进行灰关联评价,选出航道优化的最佳方案。

4 基于改进灰色关联模型的坭洲航道方案综合评价分析

4.1 灰色关联矩阵获取

利用上文构建的灰色关联评价模型对广州港出海航道的5条坭洲航道方案进行综合评价。评价模型如图1所示。

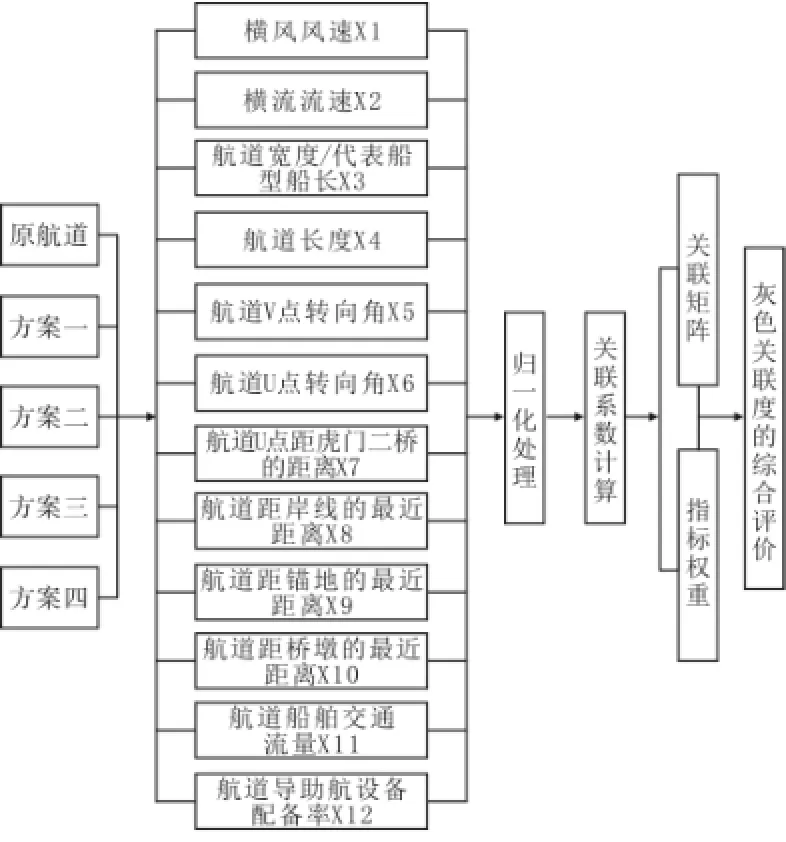
图1 坭洲航道方案比选的灰色关联评价模型

为了更准确地实现灰色关联度的算法,通过程序运行对原始数据进行处理和计算,最终得到准确的备选航道方案与比较航道方案的灰色关联度矩阵,再将得到的组合权重输入程序,获取各方案的灰色关联度排序,进而遴选出最佳的坭洲优化航道方案。

(1)通过对虎门港坭洲航道通航现状分析,根据所选取的12个评价指标的原始数据,列出相关联因子的判断矩阵:

根据以上航道评价指标的原始数据矩阵分析,选取各个指标因子的最佳数值构建得出理想方案的参考数列向量:

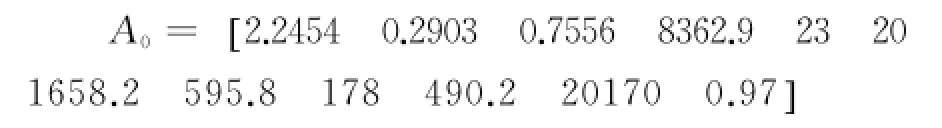
(2)通过分析本文所选的评价指标可知,其指标数列的类型和纲量存在不一致现象,为了能够进行比较和计算,需对矩阵内的原始数据规范化处理,将其转化到一个标度上,达到数据的无量纲化处理目的。数据转化公式如下:

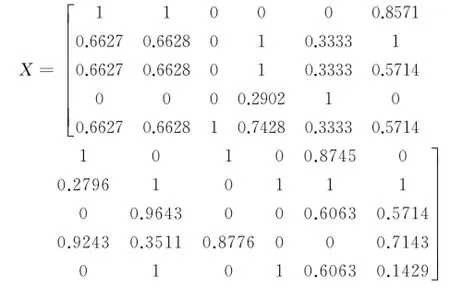
根据正、负向指标公式得到规范化矩阵:

③将理想评价数列x0＝{x0(j)|j＝1,2,3 ···,n}作为评价基准,将各个方案序列xi＝{xi(j)|i＝1,2,3···,n;j＝1,2,3···,m}作为比较数列,计算xi(j)与x0(j)的灰色关联系数:

式中:ρ为分辨系数,通常取0.5。

根据上式分别计算备选方案与比较方案的灰色关联系数:

①原航道方案与理想方案的关联系数如表1所示。

原航道方案序列:

x1＝[1 1 0 0 0 0.8571 1 0 1 0 0.87545 0]

表1 x1(j)与x0(j)的灰色关联系数序列

②航道方案一与理想方案的灰色关联系数如表2所示。

方案一序列:

x2＝[0.6627 0.6628 0 1 0.3333 1 0.2796 1 0 1 1 1]

表2 x2(j)与x0(j)的灰色关联系数序列

③航道方案二与理想方案的灰色关联系数如表3所示。

方案二序列:

x3＝[0.6627 0.6628 0 1 0.3333 0.5714 0 0.9643 0 0 0.6063 0.5714]

表3 x3(j)与x0(j)的灰色关联系数序列

④航道方案三与理想方案的灰色关联系数如表4所示。

方案三序列:

x4＝[0 0 0 0.2902 1 0 0.9243 0.3511 0.8776 0 0 0.7143];

表4 x4(j)与x0(j)的灰色关联系数序列

⑤航道方案四与理想方案的灰色关联系数如表5所示。

方案四序列:

x5＝[0.6627 06628 1 0.7428 0.3333 0.5714 0 1 0 1 0.6063 0.1429]

表5 x5(j)与x0(j)的灰色关联系数序列

对以上计算数据整理得到灰色关联度矩阵:

4.2 灰色关联度计算

本文在研究坭洲优化方案综合评价模型时,将传统的灰色评价模型进行了改进。由于评价指标存在一定的相关性,传统的灰色关联度计算方法往往在指标赋权缺乏科学依据,容易导致各个指标因子的权重不能够客观地反映出真实比重,导致评价结果的误差。

为了克服传统灰色关联度的缺陷,本文对原公式进行了改进,得到兼顾指标权重的新灰色关联度计算公式:

其中,ωj为指标权重;ξ0i(j)为灰色关联系数。

综上所述,结合上节对灰色关联矩阵的计算和指标权重的赋值,分别得出灰色关联度矩阵和评价指标权重值向量如下。

灰色关联度矩阵:

评价指标权重向量:

根据以上所获数据,应用灰色关联度的改进公式对本文航道方案综合评价值D进行计算,结果如下:

其中,D1为坭洲原航道与理想序列的灰色关联

度;

D2为坭洲航道优化方案一与理想序列的灰色关联度;

D3为坭洲航道优化方案二与理想序列的灰色关联度;

D4为坭洲航道优化方案三与理想序列的灰色关联度;

D5为坭洲航道优化方案四与理想序列的灰色关联度。

整理得坭洲航道优化方案的综合评价值为:

D＝(D1,D2,D3,D4,D5)＝(0.5604,0.7990,0.7259,0.5642,0.7736)

4.3 综合评价分析结果

根据坭洲航道优化方案的综合评价结果分析,各备选方案与理想比较方案的灰色关联度进行比较,具体比选情况如图2所示。

由上图可知,待选航道方案与理想比较航道方案的灰色关联度大小排序为D2＞D5＞D3＞D4＞D1,即航道方案一与理想航道方案的关联性最大,原坭洲航道方案与理想航道方案的关联性最小。由于在灰色关联分析理论中,待选序列与比较序列的关联性越大则说明待选序列越符合优选的要求。因此,从各个待选航道方案与理想航道方案的关联性大小,可评价出本文研究的坭洲航道优化方案的优劣排序,依次为:航道方案一为最优,其次分别为方案四、方案二、方案三、原航道。故本文通过灰色关联分析法建模给出了坭洲航道优化方案的综合评价,比选得出航道方案一为最佳方案。

图2 各航道方案与理想方案的灰色关联度

5 结束语

根据灰色关联评价模型对坭洲航道优化方案的综合评价,遴选出的最优方案,与通过大型船舶操纵模拟器仿真试验推荐的航道方案基本一致。这验证了改进灰色关联评价模型在坭洲航道优化方案比选评价中应用的可行性,为航道方案的优选提供一种定量的研究方法,给同类型水域航道的优化方案决策提供理论参考。本研究为航道优化方案的选择提供一种科学的量化比选方法。与此同时,航道比选的研究也对改善目标水域的通航环境,预防和减少水上交通事故具有重要意义。

[1]中华人民共和国交通部.海港总平面设计规范(JTJ211—99)[S],2006.

[2]郑中义.港口船舶航行环境危险度的灰色评估数学模型[M].大连:大连海事大学出版社,2001:20－25.

[3]邓聚龙.灰理论基础[M].武汉:华中科技大学出版社, 2002:41－43.

10.3969/j.issn.1672－9846.2015.03.022

N941.5;U697

A

1672－9846(2015)03－0077－05

2015－06－22

王艳锋(1982－),男,河南驻马店人,武汉交通职业学院教师,主要从事交通信息工程及控制研究。王梦紫(1982－),女,河南洛阳人,武汉交通职业学院教师,主要从事航海职业教育研究。