车辆维护与修理的最优混合决策

徐 安，乔向明，赵长利，刘圣田，张恒海

(1. 山东交通学院 汽车研究所，山东 济南 250023；2. 山东交通学院 汽车工程学院，山东 济南 250023)



车辆维护与修理的最优混合决策

徐 安1，乔向明1，赵长利2，刘圣田1，张恒海2

(1. 山东交通学院 汽车研究所，山东 济南 250023；2. 山东交通学院 汽车工程学院，山东 济南 250023)

基于可靠性理论和优化理论，以解决车辆维护与修理混合决策为目的，将今后一定时间段内预期总费用最低设为优化目标，采用定量方法进行分析，建立数学模型。结合具体的车辆技术状况概率和费用数据，给出了计算实例。研究成果具有重要的理论意义和工程应用价值，对改进公路运输企业的维修管理水平，提高成本效益具有积极的意义。

车辆工程；维护与修理；混合决策；建模；计算实例

道路运输车辆是发展国民经济的重要交通工具之一，也是需要花费巨大代价才能维持其安全运行和正常使用的设备。据交通运输部统计，至2012年年末，我国拥有公路营运汽车1 339.89万辆[1]，每年仅用于这些车辆检修的费用，至少需要588.18亿元。公路运输企业面临着安全运行、节能减排、降低成本、提高效益等多方面的巨大压力。如何从技术与经济结合的角度出发，科学决策维修作业，为企业和社会创造更大的经济效益，是一项迫在眉睫又亟需解决的重大课题。

为减少或预防故障的发生，需要定期进行强制性的维护；而一旦故障发生后，实际上可以有两种选择：①小修；②整车或总成大修。虽然维护和小修都能改善车辆的技术状况，但随着使用时间的推移，车辆技术状况老化的趋势仅靠维护和小修是不能逆转的。因此，只有大修才能彻底地恢复汽车及总成的完好技术状况和寿命。由于大修的技术相对复杂和经济代价高昂，所以在做出大修决定时，应非常慎重。

长期以来，国内外研究人员对车辆的维护与修理决策问题进行了不懈的研究，虽然车辆维护周期优化研究已取得令人满意的进展，但维护与修理决策的最优混合决策问题迄今仍未得到圆满地解决[2-14]。因此，笔者基于可靠性理论和优化理论，将今后一定时间段内预期总费用最低设为优化目标，采用定量分析和数学模型等技术手段，对此进行专门研究。

1 混合决策优化模型的建立

若假定只能在每隔一定时间的离散的时间点上，进行有关维护、小修与大修的决策。那么，希望能够确认，在每个离散的时间点上，应该做出何种决策才能使今后的n段时间内的维护、修理和运行损失总费用最低。

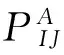
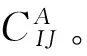
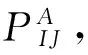
(1)

由于决策的优化目标是使预期总费用fn(I)最低，所以，最优的技术措施就是能使式(1)的值最小的那些。也就是，所谓最优，即体现如式(2)：

(2)

图1为车辆混合决策流程示意。

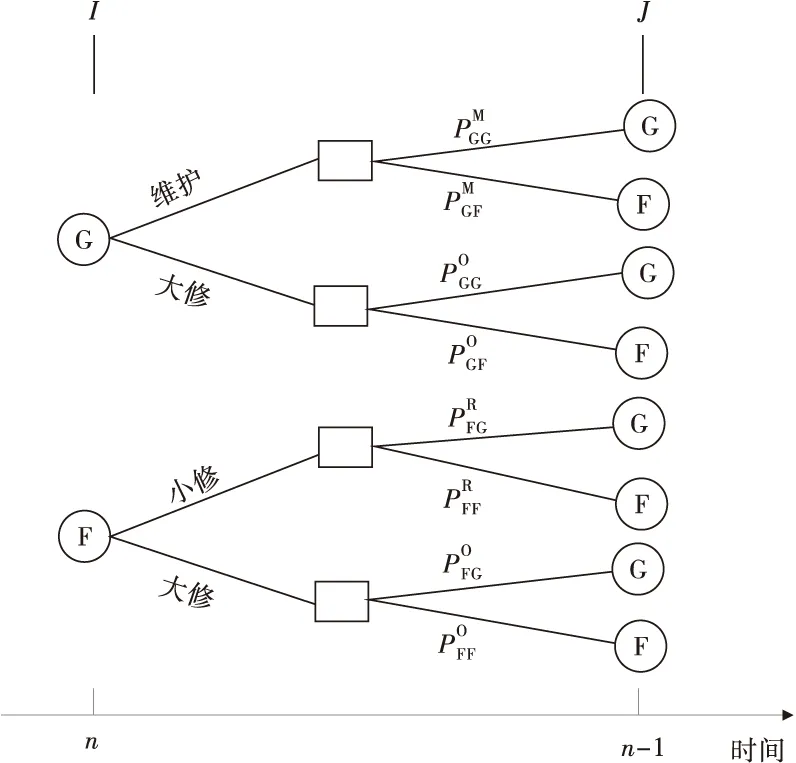
图1 混合决策Fig.1 Mixed decision

图1中，圆圈表示车辆在做出决策时可能的技术状况，其结果不外乎两种，一是完好(G)，—是故障(F)。而方块表示经一段时间的使用后，车辆可能发生故障，也可能仍保持完好。显然，在该时间段开始之初，汽车的状况I可能是完好的，也可能是处于故障状态的；同时，在该时间段结束时，也不外乎这两种情况。另外，对车辆可能采取的技术措施只有3种可供选取，它们是维护(M)、小修(R)和大修(O)。

2 数例分析计算

表1 与决策有关的概率情况

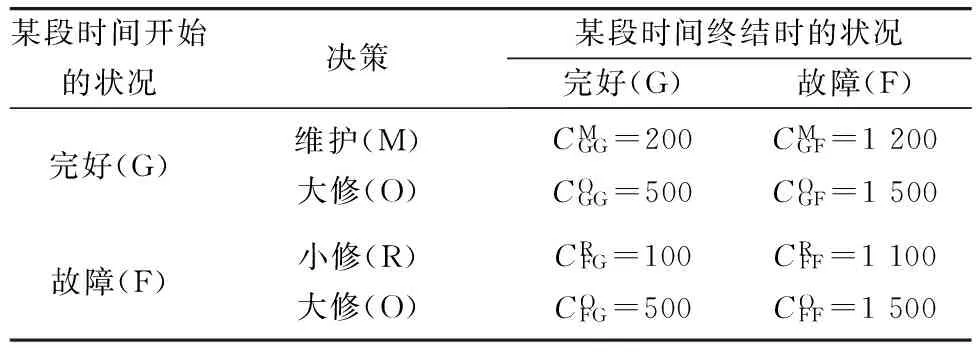
表2 与决策有关的费用情况

由表2可知，若在一段时间开始时，车辆的技术状况处于完好并进行强制维护，那么，在此期间结束时所发生的总费用仅为维护的费用，即200元。但是，若车辆在此期间出现了故障，则势必造成运行生产损失，相应的费用则变为维护和运行生产损失两项费用之和1 200元。

为了更一目了然地给出与各种可供选择的决策相应的概率和费用情况，可换用图2。

若希望为今后的4段车辆运行时间确定最优的维修决策，以便使预期的总费用为最低时，可利用递推法逐步求解。

当车辆目前的技术状况为完好，且欲使其再运行一个时间段时，如图2可知，做出维修决策时，有两种可能的选择，一是强制维护，一是大修。

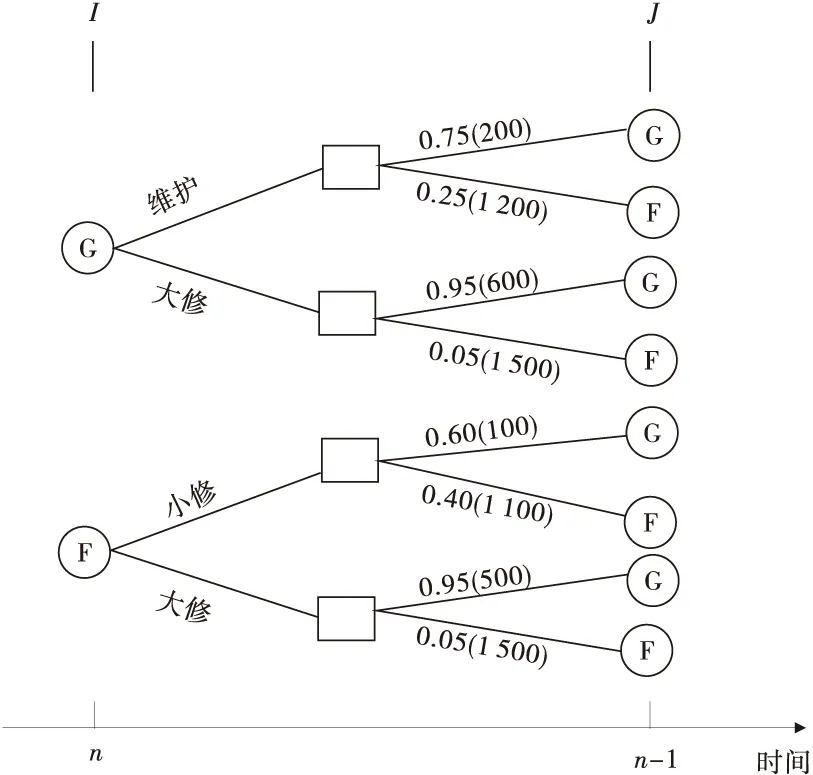
图2 混合决策的概率与费用Fig.2 Probability and costs of mixed decision

从式(2)出发，有：

若采取定期强制维护，则有：

0.25×1 200=450(元)

若采取大修措施，则有：

0.05×1 500=550(元)

如此一来，就有：

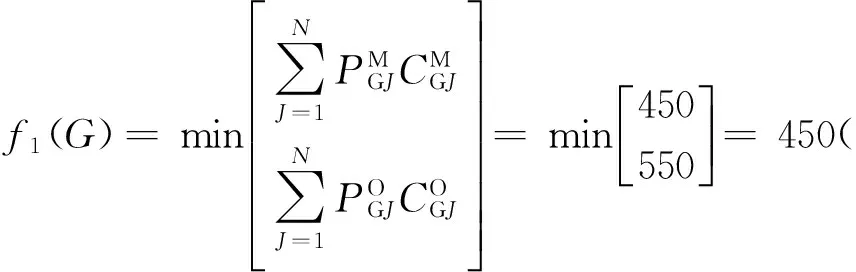
因此可确认，为使今后一段时间的车辆预期总费用最低，应选取的维修决策是定期强制维护，因为从总费用最低的目标意义上来看，它毫无疑问是最优的。

若车辆目前的技术状况为故障，且欲使其再运行一个时间段时，由图2可知，做维修决策时，也有两种可能的选择，一是小修，—是大修。从式(2)出发，有：

若采取小修，则有：

0.40×1 100=500(元)

若采取大修，则有：

0.05×1 500=550(元)

如此一来，就有：

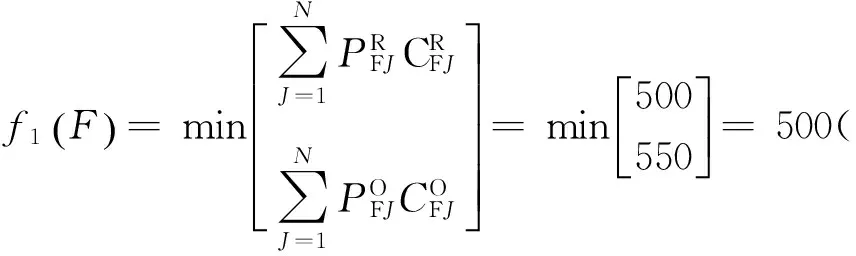
由此得出结论，为使今后一段时间的车辆预期总费用最低，应选取的维修决策是小修。

当从现在起要连续运行两段时间时，式(2)变为以下形式，即：

若车辆目前的技术状况为完好，且欲使其再连续运行两个时间段时，有：

f2(G)=

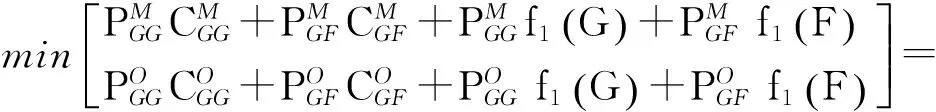
912.5(元)

所以，此前提条件下的最优维修决策为定期强制维护。

若车辆目前的技术状况为故障，且欲使其再连续运行两个时间段时，有：

f2(F)=

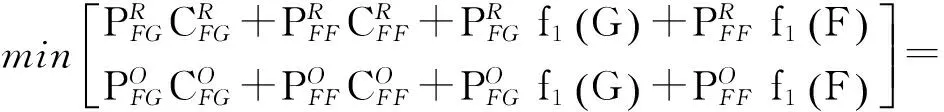
970.0(元)

因而，这时最优的维修决策为小修。

依此类推，可求出距目前时刻为n个时间段时，欲使预期的总费用fn(I)为最低的最优维修决策。表3是基于表1和表2的各项概率与费用假设，且当n=1，2，3，4时所做出的维修决策，以及相应的预期总费用。

最后应指出的是，表3中所列举的最优维修决策，仅是在给定的概率及费用前提下得出的。若前提条件不同，结论亦会有所不同。

表3 不同时间段时的最优维修决策及预期总费用

3 结 语

通过车辆维护与修理最优决策分析，并运用已建立的优化模型，完全可以在总费用最低的优化目标要求下，圆满解决车辆维护与修理的决策问题。利用具体的车辆技术状况概率和费用数据，给出一计算实例。决策模型和计算实例表明，该混合决策方法的应用性强，对汽车的维护与修理决策具有指导意义。

[1] 交通运输部综合规划司．2012年公路水路交通运输行业发展统计公报[R]．北京:中华人民共和国交通运输部，2013． Comprehensive Planning Division of Ministry of Transport of the People’s Republic of China.2012 Highway and Waterway Transport Industry Statistical Bulletin[R].Beijing:Ministry of Transport of the People’s Republic of China,2013.

[2] 徐安，梁恩忠，杨万凯．载货汽车最优二级维护周期的研究[J]．中国公路学报，1993，6(4):65-71． Xu An,Liang Enzhong,Yang Wankai.On the optimum class II maintenance period of truck[J].China Journal of Highway and Transport,1993,6(4):65-71.

[3] 徐安，乔向明．车辆维护周期多目标优化研究[J]．汽车工程，2001，23(6):427-429． Xu An,Qiao Xiangming.Multi-objective optimization of vehicle maintenance interval[J].Automotive Engineering,2001,23(6):427-429.

[4] Wang Hongzhou.A survey of maintenance policies of deteriorating systems[J].European Journal of Operational Research,2002,139 (3):469-489.

[5] 韩帮军,范秀敏,马登哲.有限时间区间预防性维修策略的优化[J].上海交通大学学报,2003,37(5):679-682. Han Bangjun,Fan Xiumin,Ma Dengzhe.Optimal policy research of preventive maintenance in finite time horizon[J].Journal of Shanghai Jiaotong University,2003,37 (5):679-682.

[6] 徐安.汽车检测诊断频率优化研究[J].公路交通科技,2000,17(6):69-72. Xu An.On optimum frequency of vehicle detecting test and diagnosis[J].Journal of Highway Transportation Research and Development,2000,17(6):69-72.

[7] 徐安.基于贴现准则的车辆大修间隔里程优化[J].公路交通科技,2001,18(6):103-107. Xu An.The optimum of vehicle overhaul interval mileage based on discount criterion [J].Journal of Highway Transportation Research and Development,2001,18(6):103-107.

[8] 高崎.炮兵武器系统维修保障及其决策方法研究[D].南京:南京理工大学,2006. Gao Qi.Research on Maintenance Support Methods and Decision-Making Methods of Artillery Weapon System[D].Nanjing:Nanjing University of Science and Technology,2006.

[9] Pascual R,Ortega J H.Optimal replacement and overhaul decisions with imperfect maintenance and warranty contracts[J].Reliability Engineering & System Safety,2006,91 (2):241-248.

[10] 吴昊.民用飞机规划维修技术理论及应用研究[D].南京:南京航空航天大学,2009. Wu Hao.Research on Theory and Application of Civil Aircraft Maintenance Planning[D].Nanjing:Nanjing University of Aeronautics and Astronautics,2009.

[11] 徐安，乔向明.有效性目标下的车辆最优维护周期研究[J].交通运输工程学报,2008,8(2):23-26. Xu An,Qiao Xiangming.Vehicle optimum maintenance period research under availability objective[J].Journal of Traffic and Transportation Engineering,2008,8(2):23-26.

[12] 郑建祥.基于可靠性和经济性的城市公交车辆维修策略研究[D].镇江:江苏大学,2012. Zheng Jianxiang.Study on Maintenance Policy of City Bus Based on Reliability and Economy [D].Zhenjiang:Jiangsu University,2012.

[13] 王礼军.模糊神经网络专家系统在故障诊断中的应用[J].重庆交通大学学报:自然科学版,2012,31(3):469-472. Wang Lijun.Application on Fuzzy Neural Network Expert System in Fault Diagnosis[J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(3):469-472.

[14] 印洪浩,彭中波.基于小波网络的船舶柴油机燃油系统故障诊断[J].重庆交通大学学报:自然科学版,2012,31(2):349-352. Yin Honghao,Peng Zhongbo.Fault Diagnosis of Marine Diesel Engine Fuel System Based on Wavelet Neural Network [J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(2):349-352.

Optimal Mixed Decision of Vehicle Maintenance and Repair

Xu An1, Qiao Xiangming1, Zhao Changli2, Liu Shengtian2, Zhang Henghai2

(1. Automotive Research Institute, Shandong Jiaotong University, Jinan 250023, Shandong, China; 2. Automotive Engineering College, Shandong Jiaotong University, Jinan 250023, Shandong, China)

Based on reliability theory and optimization theory, with the purpose to solve the mixed decision problem of vehicle maintenance and repair, the optimization goal was to make the expected total cost lowest in a certain future period of time, and the quantitative methods was used to analyze, at last the optimal mathematical models were established. Combined with the specific technical condition probability of vehicles and cost data, calculation examples are given. The research has important theoretical significance and engineering practical value, and it is of positive meaning to improve the maintenance management level, and to increase cost-effectiveness of road transport enterprises.

vehicle engineering; maintenance and repair; mixed decision; modeling; calculation example

10.3969/j.issn.1674-0696.2015.02.35

2013-09-02；

2013-12-17

交通运输部西部交通建设科技项目(20081800074)；山东省交通科技创新计划项目(201233-6)

徐 安(1955—)，男，四川仁寿人，教授，主要从事汽车可靠性、维修性、安全性方面的研究。E-mail：xuan7230@163.com。

U472.4

A

1674-0696(2015)02-161-04