基于已知球面波前的Hartmann-Shack传感器结构参量标定
2015-06-09周晓斌栾亚东史雷蕾雷增强
周晓斌,栾亚东,史雷蕾,雷增强
(西安应用光学研究所,陕西 西安 710065)
基于已知球面波前的Hartmann-Shack传感器结构参量标定
周晓斌,栾亚东,史雷蕾,雷增强
(西安应用光学研究所,陕西 西安 710065)
微透镜阵列到CCD的距离是影响Hartmann-Shack波前探测器精度的主要装配误差之一。对该平移装配误差的修正,能够有效减小波前探测误差。理论求解了球面波前通过微透镜引起的子孔径光斑质心移动量与波前探测器结构参数之间的关系,借助该关系能够求出微透镜到CCD之间的实际距离,以其改进波前斜率的计算。实验验证了理论推导的合理性,并对实际装配参数进行标定,得实际距离为24.2mm。利用标定后的参数重建波前,其相对误差减小20.4%。实验表明该标定方法能够有效提高波前传感器测量准确性。
自适应光学;Hartmann-Shack传感器;波前重构;平移误差
引言
Hartmann-Shack波前探测器(H-S)普遍应用于自适应光学系统、激光光束质量判断、光学元件及光学系统检测、大气扰动探测和人眼像差的测量[1-2]。影响H-S探测精度的因素除光斑质心位置和波前重构算法外,还有其自身装配误差[3]。微透镜阵列到CCD的距离l是限制H-S测量准确性装配误差之一。一般波前斜率计算都是利用微透镜焦距fn代替该参数,但是并不能保证CCD靶面与微透镜焦面完全重合,如果简单认为l=fn会引入波前斜率计算误差,文献[4-5]对此有详细的分析。因此,对于装调完成的H-S,需要进行标定以消除系统误差。
传统标定方法是利用修正系数对波前测量值进行校正。该方法使用fn计算斜率,用该斜率对标准像差板进行波前重建,对比测量结果与实际值差异,计算通用修正系数。此方法对实验要求较高,需要多次测量统计后才能计算出系数。梁春等人提出利用点光源提供离焦波前[6],再根据Zernike模式法重建波前中离焦项系数推算出距离l。该方法依赖于波前重建算法精度。文献[7]提出利用已知斜率的平面波校准l的方法,其依靠点光源的位移量保证校准精度。
本文结合球面波前特点,理论推导了已知半径球面波前通过微透镜阵列的光斑位移量,从而反推出H-S装配结构参量l,并以实际距离代替微透镜焦距计算波前子孔径斜率,重构波前。
1 Hartmann-Shack工作原理
平面波垂直入射到微透镜阵列时,光斑分别位于子孔径中心。当畸变波前入射后,子孔径光斑位置会发生变化(Δx,Δy)。根据光斑位移和微透镜阵列到CCD距离l,可以计算波面子区域内的平均波前斜率g:
(1)
再由波前复原算法即可重构畸变波前。为了匹配微透镜阵列尺寸,通常在系统前端设置缩束系统,并与微透镜阵列和CCD探测器构成典型的Hartmann-Shack波前探测器,其工作原理如图1所示。
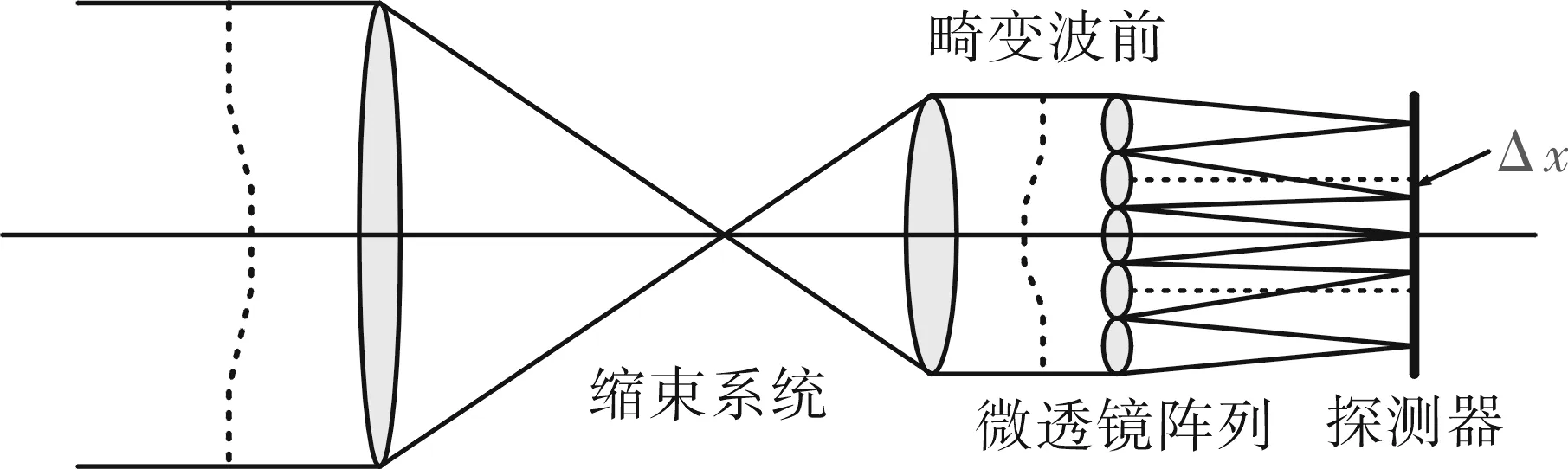
图1 Hartmann-Shack工作原理Fig.1 Principle diagram of Hartmann-Shack
利用模式法重建波前[8-9],一个完整的波前φ(x,y)可以用Zernike多项式展开为
(2)
式中:Zk(x,y)为各项Zernike多项式;ak为各项系数。要重构波前只需求出系数ak。对上式微分有:
(3)
可以得到矩阵式:
G=FA
(4)
式中:G为波前斜率向量;A为Zernike多项式的系数向量;F称为波前重构矩阵,表示Zernike多项式在x,y方向的平均斜率。由于F通常非方阵,所以需求出它的广义逆F+,从而计算出系数矩阵A。
A=F+G
(5)
2 基于球面波前的Hartmann-Shack结构参量标定
文献[10]推导出半径为R的球面波前φ(x,y)=φo-k[(x2+y2)/2R],其中波矢k=2π/λ,通过焦距fn和子孔径间隔d的微透镜阵列后,光斑质心相对于平面波前入射时的位移量。微透镜子孔径(i,j)内X方向相位差为
(6)
则由相位差引起光斑位置,在子孔径(i,j)焦面上X方向光斑中心偏移量为
(7)
所以,当汇聚或发散波前入射H-S时,光斑间距会相应缩小或增大,并且光斑仍均匀分布。
相邻两子孔径的光斑位移量之差与球面波前半径之间关系为
(8)
为了符号统一,δx引入负号即汇聚R为正,光斑间隔变小,利用(8)式便可以计算出实际装调完成后的距离l。
可由平行光管提供已知半径的球面波前。当平行光管移焦x,由牛顿公式得焦像距x′=-f2/x。根据H-S前段望远(缩束)系统光学结构参数,物镜fo、目镜fe、H-S距平行光管出瞳L等,计算得最终入射到微透镜的球面波前半径为
(9)
式中,M为H-S缩束系统倍率。
为了减小系统误差,采用差值法处理。结合(8)式、(9)式可知,当平行光管移焦量由x1变化为x2时,
(10)
从公式(10)可以看出,l与具体光路参数无关,只要已知f、d、M,测量平行光管2次移焦后相邻光斑间距变化量δx1和δx2,就可以计算出l。而l的标定误差主要由光斑间距变化量所确定。根据球面波的对称性可知Y方向关系与X方向相同。
3 实验验证
利用以上算法对一个已经装调完成的H-S进行标定。平行光管焦距f=1 600mm;H-S缩束倍率M=4;微透镜阵列焦距fn=32mm,d=1mm。光斑质心提取软件是基于CCD控制软件包自行开发的,利用Zernike模式法重建波前。
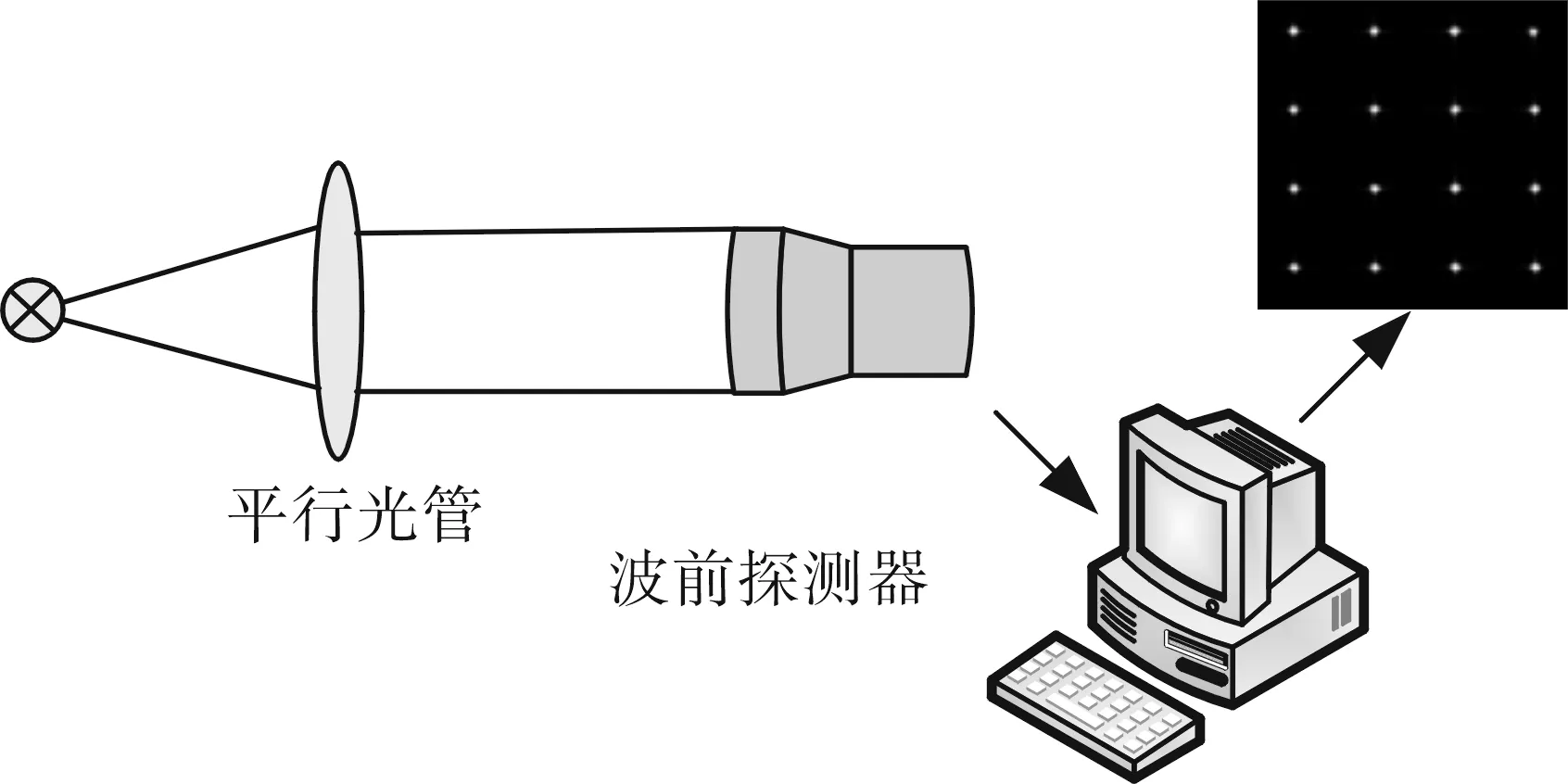
图2 实验装置示意图Fig.2 Schematic diagram of experiment setup
从图3和图4可以看出,光斑移动规律与理论推导一致,其中图4中OPD(optional path difference)表示波面光程差,发现平行光管光轴并未与H-S光轴重合。H-S测量的为球面波非对称部分,但这并不影响l的计算。因为标准球面波引起光斑移动是均匀的,只要H-S垂直于平行光管光轴即可。而平行光管和H-S视场都很小,只要保证平面波入射子区域光斑分布均匀就能满足光路要求。
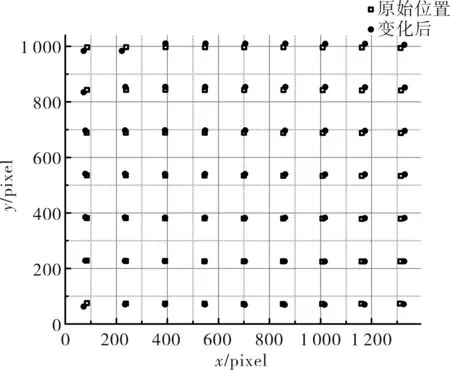
图3 平行光管移焦100 mm后光斑变化Fig.3 Spots changed before and after collimator defocus 100 mm
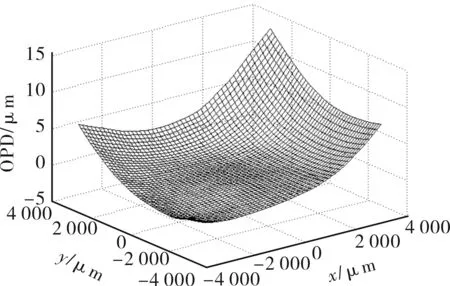
图4 移焦100 mm后波前复原图Fig.4 OPD distribution after defocus 100 mm
选取平行光管移焦40 mm、60 mm、80 mm 3组数据两两差值,由公式(10)计算得平均值l=24.2 mm。为了检验标定后的H-S测量准确性,分别用fn=32.0 mm和l=24.2 mm计算斜率,对同一波前进行重建,对比重构波前PV值和理论计算值。球面波矢高为其理论PV值。
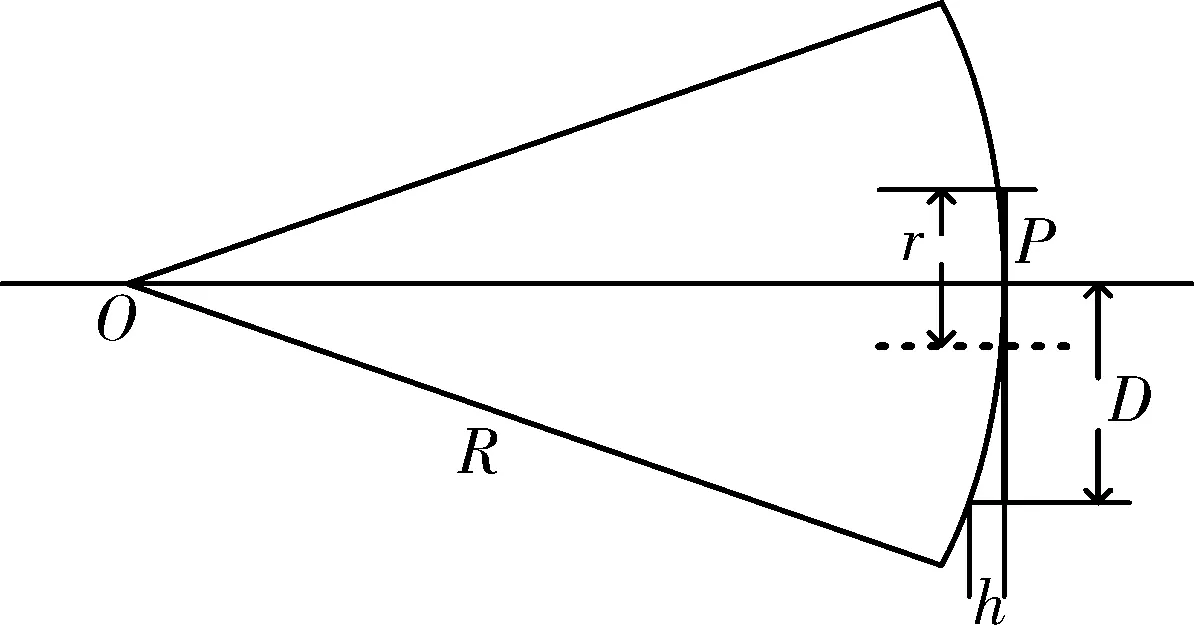
图5 H-S截取球面波矢高计算Fig.5 Rise calculation for spherical wave measured by Hartmann-Shack
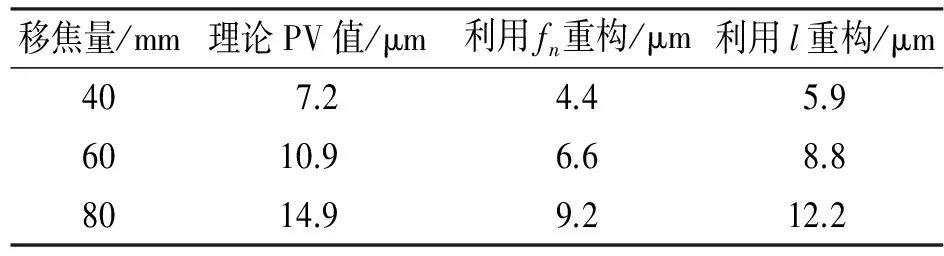
表1 重构误差对比
从上表可以看出,利用l计算斜率重构波前,相比于直接利用微透镜焦距重构,波前拟合PV值更接近理论值,相对误差减小20.4%,证明标定后波前测量准确度提高。然而,无论利用fn还是l重构,测量值相比于理论值都存在较大误差,一方面是由于球面波球心点选择造成理论计算PV值存在误差。另一方面,在重构波前系数中X方向有一定的倾斜量,会影响测量PV值。但是,在相同球心选择误差和波前倾斜量下,对l进行标定能够有效提高H-S测量准确性。
4 总结
本文研究利用已知球面波前对Hartmann-Shack波前探测器平移装配误差的标定方法。对此参数的标定可以有效提高H-S测量的可靠性和准确性。相比于传统的像差板确定修正系数,此方法原理简单,与波前重构算法无关,只需要简单的实验仪器即可实现,能够有效指导实际装调过程,降低装调精度要求。
[1] Kou Songfeng,Liu Genrong,Niu Dongsheng,et al. Design of SONG Shack-Hartmann optical system[J]. Journal of Applied Optics,2014,35(1):1-6. 寇松峰,刘根荣,牛冬生,等.“宋”望远镜夏克哈特曼光学系统设计[J]. 应用光学,2014,35(1):1-6.
[2] Guo Guangyan,Fan Zhongwei,Yu Jin,et al. Wavefront detection technology based on Shark-Hartmann theory[J]. Journal of Applied Optics,2014,35(5):823-829. 郭广妍,樊仲维,余锦,等.基于Shark-Hartmann理论的波前探测技术研究[J]. 应用光学,2014,35(5):823-829.
[3] Xia Mingliang,Li Chao,Liu Zhaonan,et al. Adaptive threshold selection method for Shack-Hartmann wavefront sensors[J]. Optics and Precision Engineering,2010,18(2):334-340. 夏明亮,李抄,刘肇南,等.Shack-Hartmann波前传感器图像自适应阈值的选取[J]. 光学精密工程,2010,18(2):334-340.
[4] Ye Hongwei,Xian Hao,Zhang Yudong. Study on translation error of Hartmann-Shack wavefront sensor[J]. Opto-Eletronnic Engineering,2003,30(2):1-10. 叶红卫,鲜浩,张雨东. 对Hartmann-Shack波前传感器平移误差的研究[J]. 光电工程,2003,30(2):1-10.
[5] Dai Yang,Li Faquan,Cheng Xuewu,et al. Assembly error of Hartmann-Shack sensor[J]. High Power Laser and Particle Beams,2006,18(9):1469-1474. 戴阳,李发泉,程学武,等. Hartmann-Shack传感器组装误差分析[J]. 强激光与粒子束,2006,18(9):1469-1474.
[6] Liang Chun,Sheng Jianxin,Tong Gui,et al. A self-reference method for measuring Hartmann-Shack warefront sensor parameter[J]. Acta photonica sinica,2009,38(4):780-784. 梁春,沈建新,童桂,等. Hartmann-Shack传感器结构参量的自基准标定[J]. 光子学报,2009,38(4):780-784.
[7] Wang Yanping,Wang Qianqian,Ma Chong. Study on hartmann wavefront analyzer calibration method[J]. Chinese Journal of Lasers,2015,42(1):0108003-1-0108003-7. 王艳萍,王茜蒨,马冲. 哈特曼波前分析仪校准方法研究[J]. 中国激光,2015,42(1):0108003-1-0108003-7.
[8] Zhou Renzhong. Adaptive optics[M]. Beijing: National Defence Industry Press,1996. 周仁忠. 自适应光学[M]. 北京:国防工业出版社,1996.
[9] Xia Aili. The study of adaptive optical system based on Shack-Hartmann wavefront sensor[D]. Xi’an:Xi’an Institute of Optics and Precision Mechanics of CAS,2011. 夏爱丽. 基于Shack-Hartmann波前传感器的自适应光学系统研究[D]. 西安:中国科学院西安光学精密机械研究所,2011.
[10]Wan Min,Zhang Jiaru,Zhou Ke’en,et al. Calibrate plane beam using Hartmann-Shack method[J]. High Power Laser and Particle Beams,1997,9(3):443-446. 万敏,张家如,周克恩,等. 用哈特曼-夏克法标定平面光束[J]. 强激光与粒子束,1997,9(8):443-446.
Structural parameters calibration of Hartmann-Shack sensor based on known spherical wavefront
Zhou Xiaobin,Luan Yadong,Shi Leilei,Lei Zengqiang
(Xi’an Institute of Applied Optics,Xi’an 710065,China)
The distance between the charge couple-device (CCD) and the micro lens array is one of the assembling errors which affects the accuracy of Hartmann-Shack wavefront detector. The correction of this motion assembly parameter can effectively reduce the wavefront detector error. The relationship between the subaperture spot centroid shift amount,caused by the spherical wavefront passing through the micro lens, and the structural parameters of wavefront sensor was derived theoretically. By utilizing the relationship, it is able to work out the actual distance from the CCD to the micro lens array and improve the calculation of the slope of wavefront. Experiments verified the rationality of theoretical derivation, and the actual assembly parameter calibrated is 24.2 mm. The wavefront was reconstructed by the calibrated parameter, the relative error can reduce by 20.4%. Experiment results show that the calibration method can effectively improve the measurement accuracy of wavefront sensor.
adaptive optics; Hartmann-Shack sensor; wavefront reconstruction; motion error
1002-2082(2015)06-0909-04
2015-06-11;
2015-08-30
周晓斌(1989-),男,陕西岐山人,硕士研究生,主要从事光学系统设计工作。E-mail:xbin205@163.com
TP
A
10.5768/JAO201536.0603002
