CORDIC算法在数字频率合成中的应用研究与实现

马思强，王首斌，邵国峰

（中国电子科技集团公司第三十六研究所，浙江嘉兴314033）

CORDIC算法在数字频率合成中的应用研究与实现

马思强，王首斌，邵国峰

（中国电子科技集团公司第三十六研究所，浙江嘉兴314033）

相较于传统的基于ROM查找表的数字频率合成方案，采用CORDIC算法来计算正余弦函数时，无需使用乘法器，只需要一个最小的查找表（LUT），利用简单的移位和相加运算，即可产生高精度的正余弦波形，可以有效节省存储资源，非常适合于在FPGA上实现。在CORDIC算法研究的基础上，合理设计了CORDIC电路的实现结构，并通过Verilog HDL语言进行了硬件描述设计，整个设计方案通过算法验证并最终在Altera Stratix II系列EP2S130F1020C5型FPGA上完成了布局布线，最高工作频率为145.2MHz。

CORDIC；FPGA；三角函数

0 引言

近些年来，随着集成电路技术的发展，坐标旋转数字算法（CORDIC）的优势越来越明显，因此它被广泛应用于数字信号处理领域。

CORDIC算法是用于计算广义矢量旋转的一种迭代方法，最早由Volder于1959年提出［1］，在此基础上Walther提出了统一的CORDIC算法［2］，并将CORDIC实现的三种功能：三角函数运算、双曲运算和线性运算统一于一个表达式中，形成了CORDIC算法的基本数学基础。CORDIC算法的基本思想是通过一系列角度的旋转来逼近目标角度，并且这一系列的角度是预先经过挑选设定的，这一旋转过程可以通过移位和加减法运算的方法实现。所以针对实现复杂功能运算，利用CORDIC算法能够取得较好的硬件资源节约效果。

1 CORDIC算法原理

CORDIC算法的基本原理可以通过极坐标的形式进行说明，已知一个目标点（Xn，Yn）通过旋转角度θn后可以达到另一个点，记作（Xn+1，Yn+1），这一旋转过程可以通过矩阵的形式表示，具体为：

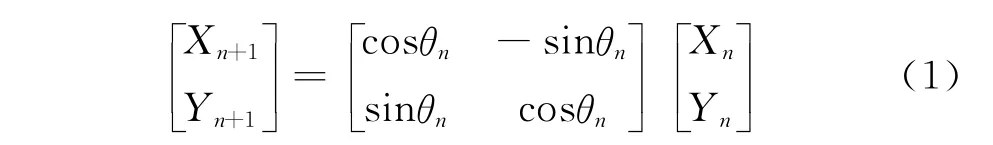
将cosθn提出，从而可以得到：

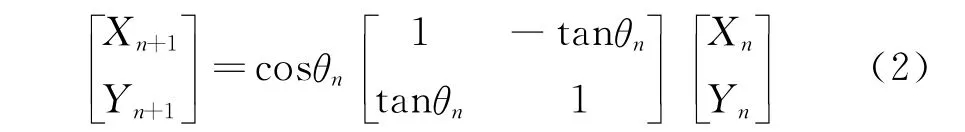
如果取θn=arctan（2-n），并将θn定义为每一次旋转的角度，则所有迭代旋转角度的总和θ可以表示为：

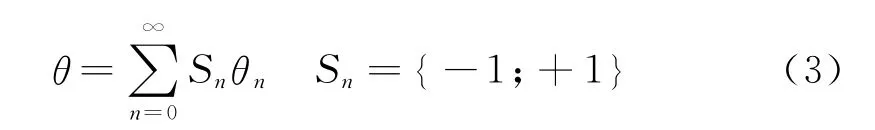
此时式（2）中的tanθn=Sn2-n，则式（2）可以转换为：

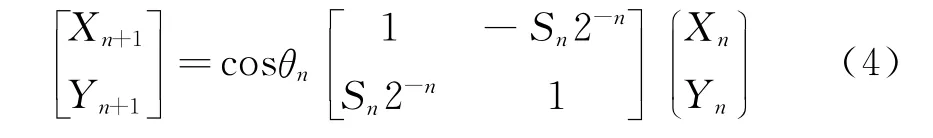
式中，cosθn=cos（arctan（2-n）），随着迭代次数的增加，该式可以收敛为一个常数：

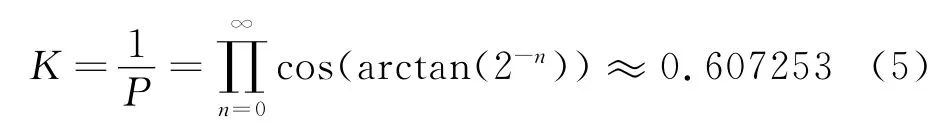
可以暂时不考虑这个增益常数K，这时式（5）可以改写为：

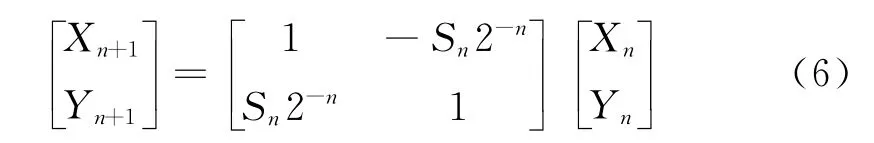
这里用Z来表示相位累加的部分和，则可以得到：

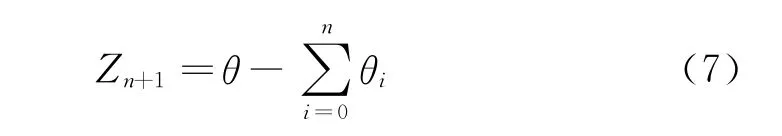
因此可以给出CORDIC算法最核心的三个迭代公式为：

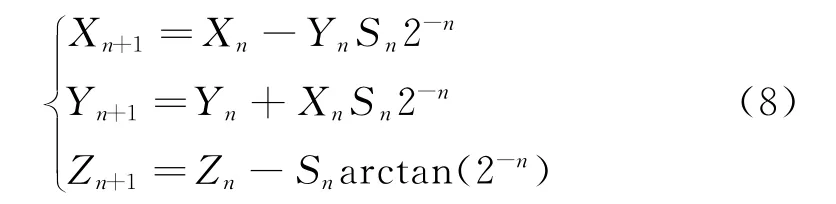
如果想将Z最终旋转到0，则Sn的取值由Zn决定，具体表现如下：

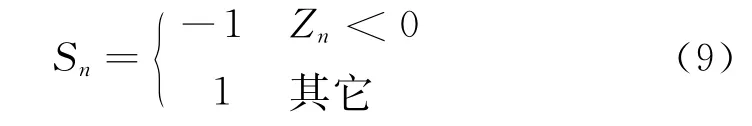
通过上面的分析，经过多次旋转之后，最终的表达式结果可以总结为：

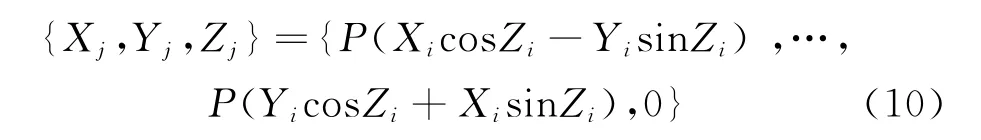
如果取一组特殊的初始值：

通过若干次迭代旋转之后，使得Z最终旋转到0时，则可以得到最终结果为：

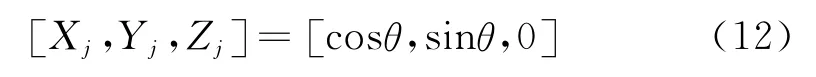
一般将这种工作模式称为旋转工作模式。如果取如下的初始值：

并通过不断旋转使得Y趋近于0，Sn的取值由Yn决定，具体表现如下：

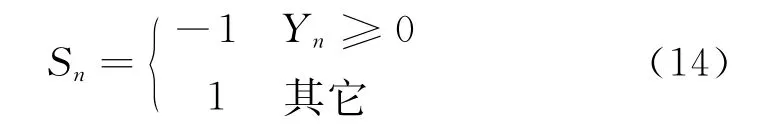
通过若干次迭代旋转之后，使得Y最终旋转到0时，则可以得到最终结果为：

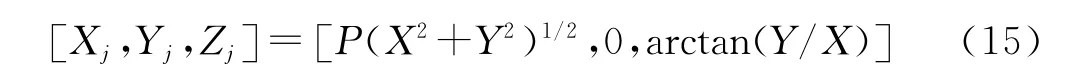
通过这种方式可以得到已知向量的幅值和相角，这种模式被称为向量工作模式。

2 CORDIC算法的角度范围

在具体应用CORDIC算法时，该算法所能旋转的角度是有界限的。这里假设算法迭代次数为N，那么通过N次旋转之后可以得到的角度范围为［3］：

通过进一步的取极限运算，这个角度范围将收敛至［-99.88°，99.88°］。这样如果采用CORDIC算法，并基于旋转模式进行求解已知角度θ的正弦和余弦值时，就要求θ的取值范围满足［-99.88°，99.88°］。而一般意义上来说θ的取值范围应该为［-π，π］，因此有必要利用三角函数特性对角度输入信号进行相关处理，使得其满足CORDIC算法关于输入角度的范围限制。

3 CORDIC算法的硬件实现

基于CORDIC算法的三角函数合成方法相较传统的查找表法具有高精度、低存储资源消耗的特点。由于整个算法主要由基本的加、减法和移位操作组成，因此十分适合VLSI实现。图1所示为本文设计的数字频率合成器（CORDIC）模块的端口信号示意图。为了满足设计电路的高速处理需要，本文确定了基于多级流水的CORDIC结构设计方案。为了计算输入的瞬时相位信息所对应的正余弦函数值，CORDIC模块将工作在旋转模式。本文所设计的CORDIC模块依然工作在系统时钟100MHz环境下，且由系统复位信号rst_n对内部寄存器进行复位操作。

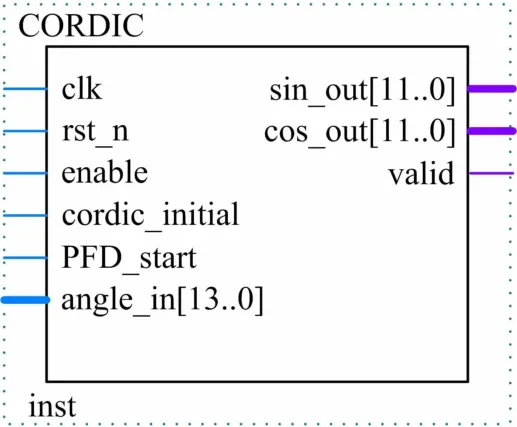
图1 CORDIC模块的端口信号示意图

关于CORDIC算法迭代次数的选取及其精度分析，众多文献［4-5］给出了证明和结论。总体来说，CORDIC算法的迭代次数跟所表达角度值的小数位比特宽度有关。如果想要分解由b个比特小数位表示的角度值，CORDIC算法所选取的迭代次数N应该大于或等于b+1。这是由于如果角度可以被多次分解，则其最小精度单位2-b应该有意义。经过CORDIC算法多次迭代操作之后，最后一次迭代中的θn-1应该小于或等于2-b。当θn-1足够小时，其值可取2-（n-1）来近似，因此可以得到迭代次数N与角度小数位宽度b之间的关系。由于本文把输入的瞬时相位的小数位宽度确定为11个比特，因此在具体设计中采用了12次迭代来实现CORDIC算法。

由于输入相位θ的范围为［-π，π］，而根据前面内容可知，CORDIC算法输入角度的取值范围应为［-99.88°，99.88°］，所以本文在进行CORDIC模块设计时预先采用逻辑单元将输入角度θ进行旋转，使其旋转后得到的角度φ保持在区间［-π/4，π/4］之内。在CORDIC模块输出端可以利用三角函数特性，通过逻辑单元将φ对应的三角函数输出结果转换为原始相位θ所对应的正余弦值。图2给出了本文所设计的CORDIC模块结构原理图。

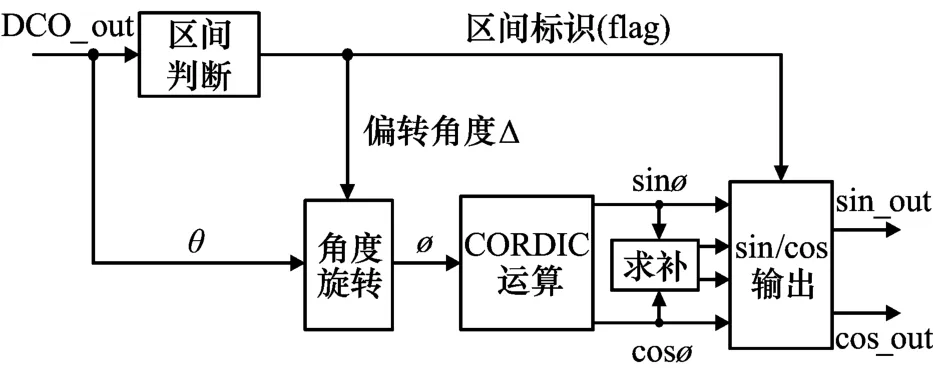
图2 CORDIC模块的结构原理图

为了使得本文所设计的CORDIC模块能够在系统时钟100MHz下正常运转，因此有必要使得整个模块的最大路径延时低于10ns。经计算，如果采用12次迭代过程，不打任何流水的整个路径将会耗时33ns左右，如果每次迭代过程均打一次流水，则需要耗费12个系统时钟周期完成CORDIC运算。为了降低模块运算时间，本文按照图3所示在12级迭代中均匀打入了4级流水，使得最大路径延时保持在8ns左右。这样既满足了系统速度需要，也提高了模块的运算效率。此外，加上模块内相位旋转的1级流水，在具体运行过程中，本文所设计的CORDIC电路只需要消耗5个系统时钟周期就可以完成全部的运算处理工作。

硬件实现部分，本文运用Verilog HDL语言，采用自上而下的设计原则，对整个方案进行了硬件描述。并利用ModelSim软件进行功能仿真。在设计CORDIC模块时，为了缩短最大路径延时进而使得系统最大工作频率高于100MHz，本文在CORDIC算法12次迭代路径上打入了4级流水，加上对原始相位输入进行旋转操作的1级流水，整个CORDIC模块共采用5级流水结构进行设计。图4所示为CORDIC模块输出的正余弦信号图。可以看出，本文所设计的CORDIC模块根据瞬时相位实时地输出对应的正余弦值。从波形可以看出，CORDIC模块输出正余弦曲线十分平滑，达到了预期的设计功能。

功能仿真验证后，本文运用Synplify Pro软件在Altera Stratix II系列EP2S130F1020C5型FPGA上对设计方案进行了综合和布局布线。实现过程所消耗FPGA资源情况如表1所示。系统布线后最高时钟可达145.2MHz。

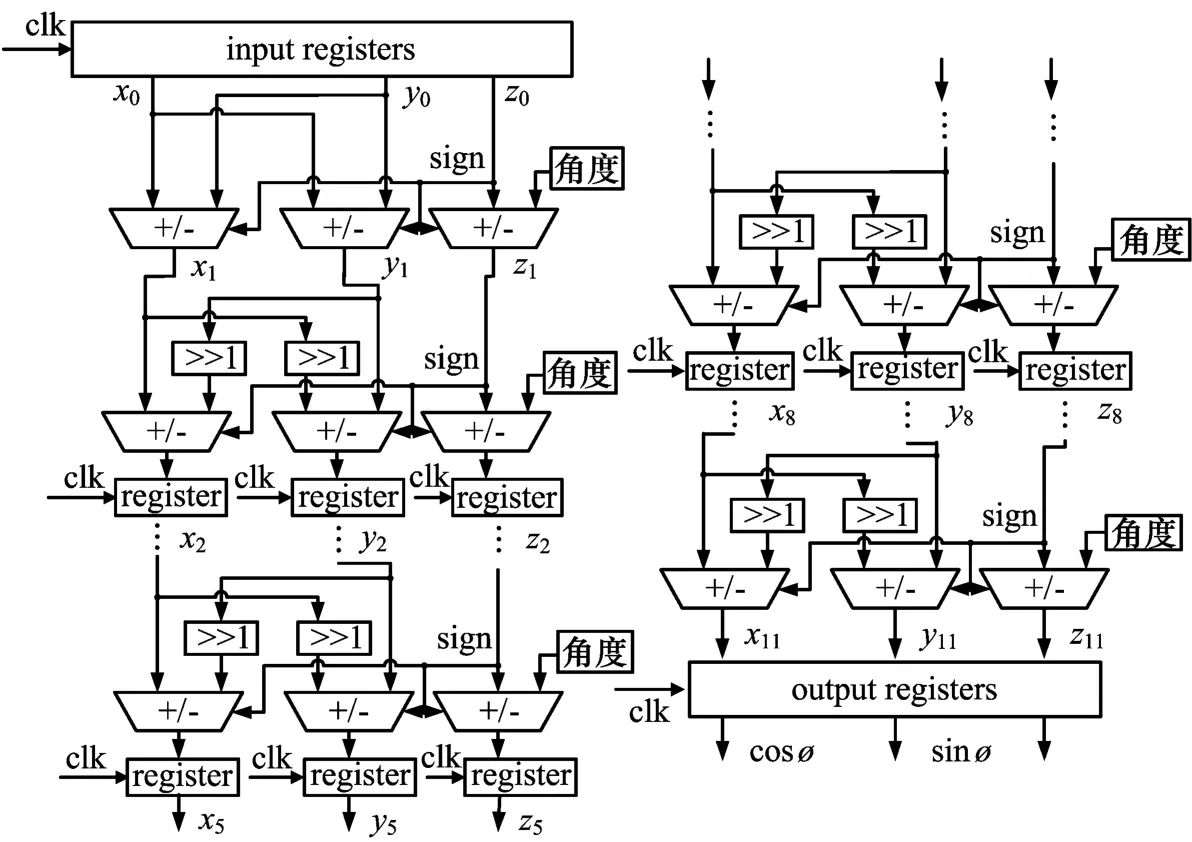
图3 本文所设计CORDIC电路结构图

表l 占用硬件资源统计

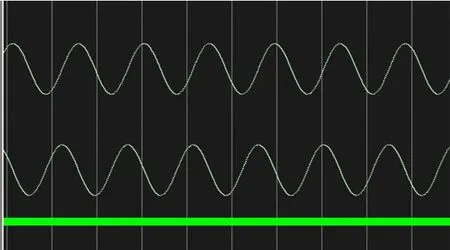
图4 CORDIC模块输出正余弦信号

4 结束语

本文针对CORDIC算法在数字频率合成方面的应用进行了研究。结合算法研究，考虑高速数字电路设计原则，运用Verilog HDL语言对本文方案进行了寄存器传输级描述，并完成功能仿真。设计方案最终在FPGA上实现。仿真与硬件实现结果证明了本文所提出的设计方案具备良好的性能与可行性。■

［1］ Duhamael P，Vetterli M．Fast Fourier transforms：a tutorial review and a state of the art［J］．Signal Processing，1990（19）：259－299．

［2］ Ercegovac MD，Lang T．Implementation of fast angle calculation and rotation using on-line CORDIC［J］．IEEE International Symposium on Circuits and Systems，1988，3：2703－2706．

［3］ Brennan PV，Walkington R，Borkjak A．Performance of PLL synthesiser based on DDS feedback［J］．IEEE Electronics Letters，1998（34）：2197－2199．

［4］ 张炜，杨虎．基于CORDIC算法的直接数字频率合成器实现方法［J］．重庆邮电学院学报，2006，18（5）：597－600．

［5］ Hu YH．The quantization effects of the CORDIC algorithm［J］．IEEE Trans．on Signal Processing，1992，40（4）：834－844．

Research and implementation of CORDIC algorithm on DDFS

Ma Siqiang，Wang Shoubin，Shao Guofeng
（No.36 Research Institute of CETC，Jiaxing 314033，Zhejiang，China）

CORDIC algorithm is more accurate and more feasible on FPGA implementation than conventional look-up tables，which only needs a smallest LUT.Based on the study of CORDIC algorithm，the CORDIC circuit is designed.The whole design is synthesized under Altera Stratix II EP2S130F1020C5 FPGA. Highest clock frequency after routed can reach 145.2MHz.

CORDIC；FPGA；trigonometric

TN97；TN79

A

2015-05-26；2015-07-16修回。

马思强（1987-），男，工程师，博士，主要从事电子系统总体设计、信号处理技术等方面的研究工作。