第三方检验费用线性回归分析
2015-06-09叶芬李凯
叶芬,李凯
中海石油海南天然气有限公司
第三方检验费用线性回归分析
叶芬,李凯
中海石油海南天然气有限公司
近年来,第三方检验服务广泛应用于LNG设备、材料采购环节。通过买卖双方之外的第三方检验服务机构,对产品的品质、数量、包装、标记等进行验证的一种公证服务,已成为采购环节不可缺少的组成部分。因此,对第三方检验机构的管理是采购环节中重要的工作内容,其管理内容涉及到所购买产品的质量控制、产品供货周期、项目建设周期、项目建设投资等众多方面。因此,哪些因素为检验主要影响因素,如何对设备材料第三方检验费用进行控制的前提下,达到较好的检验效果也显得尤为关键。本文列举一些常见的对检验费用产生影响的因素,并对其进行分析,最终得出各因素影响程度,并得出预测方程。进而分析检验管理方法和手段。
第三方检验;费用;线性回归
1 概述
1.1 项目背景
海南LNG项目是由中海石油气电集团有限公司投资的海南省规划建设的重点能源项目。项目占地57.2公顷,工程总投资约65亿元人民币;包括1座可停靠26.7万立方米LNG船舶的接卸码头和1座3000吨级工作船码头及其配套设施;2座16万立方米的LNG储罐及其配套设施;新建输气管线122公里。项目总计120多个采办包,300多家投标单位及供应商,设备材料购置费用总计约10亿元,占项目总投资约15.4%。这些设备材料的质量将直接影响到项目的施工质量,后期运行等各个方面。并且设备材料的供应商分布于近20多个国家和地区,负责这些设备材料采购工作的技术人员仅十余人,人员较为年轻,工作经验不足。因供应商众多、空间跨度较大、企业人员短缺、经验不足等原因,业主直接对供应商进行检验支出费用将产生巨额的费用以及人力支出,可以说根本无法完成对供应商的直接质量监管,必须借助第三方质量检验机构对供应商产品进行检验。
1.2 理论基础
在统计学中,线性回归是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为简单回归,大于一个自变量情况的叫做多元回归。在线性回归中,数据使用线性预测函数来建模,并且未知的模型参数也是通过数据来估计。这些模型被叫做线性模型。
1.3 问题分析
第三方检验机构与海南LNG的合作、对接还面临着很多挑战。例如,高速的发展催生了林立的检验机构和庞大的检验从业人员,也同时产生了技术水平参差不齐;因文化差异、运作模式等原因而导致的沟通渠道不畅通等诸多问题。这些问题不仅涉及到对业主购买的产品质量的控制,还将牵涉产品供货周期、项目建设周期、项目建设投资、检验费用支出等众多关乎项目整体进度、费用等重要方面。基于第三方检验的重要性和其本身存在的问题,业主对加强第三方检验机构监管的需求也在逐渐增加。
限于客观条件的制约,加强第三方检验管理的主要手段和方法之一就是对检验费用进行控制,通过对检验费用的预估和调整,以示激励或惩罚,从而做到对检验人员的正向或负向刺激,以达到控制检验质量的目的。因此,出于对检验费用预估、评价等方面的考量,对检验费用进行多元回归分析。
2 第三方检验费用多元回归分析
2.1 确定变量
a)因变量Y:检验费用
设检验费用为因变量Y,并根据已产生费用的实际经验,将检验费用分为四个等级,检验费用约多,级别越高。
1~5万1级
5~10万2级
10~15万3级
15~20万4级
b)自变量
根据实际情况,设5个自变量X1~X5。
1)自变量X1:设备、材料等级
设备的重要程度通过检验难度,检验时间长短,检验项目多少等方式反馈至因变量检验费用。根据专家评定的设备、材料等级分为四个等级。评分档次按照设备重要性确定,重要性越低,评分就越高,设备等级数就越大。
0~25分为1级
25~50分为2级
50~75分为3级
70~100分为4级
2)自变量X2:地区差异
检验地区不同,检验员的人工单价也不同,对最终的检验费用有重要影响。根据实际国家情况,检验费用单价分为九个地区:北欧、西欧、中欧、南欧、东亚、日本、北美、澳洲和国内。检验费单价从2800起至9300元不等。因部分地区人工单价差异不大,且因为商业保密原因,不严格按照地区进行细分列举,仅将这九个地区的人工单价分为四个级别:
0~3000元(含)1级
3000~6000元2级
6000~9000元3级
9000元以上4级
3)自变量X3:检验见证项目
检验见证的项目多少也将影响到检验费用。在实际工作中,检验见证项目通常在检验见证前就确定,并由业主、供货商、第三方检验机构共同确认,并形成正式文件:检验测试计划(ITP),后期检验过程中,仅因极特殊情况才会产生变动,一般情况下较为稳定,可以当作考评检验费用的参考依据之一。根据经验,将检查项目按照数量多少分为四个等级。
0~10个检查项1级
10~15个检查项2级
15~20个检查项3级
20个检查项以上4级
4)自变量X4:合同总价
合同总价是指采购设备、材料所签订的合同的总价,根据经验直观无法判断合同总价对检验费用的影响程度,暂将合同总价分为四个等级:
100万以下1级
100~200万2级
200~400万3级
400万以上4级
5)自变量X5:检验天数
检验天数与检验费用可直接明了的判断出其他条件不变的情况下为线性相关关系。检验天数的增加必然将导致检验费用的增加。根据天数多少,暂列为四个等级。
0~10天1级
10~15天2级
15~20天3级
20以上天4级
2.2 数据采集
选取已经完成的12个设备材料采办包,收集因变量、自变量数据。因涉及价格等商业原因,设备材料种类不列明,仅以编号代替。变量信息如下表所示:
表2-1变量数据采集表
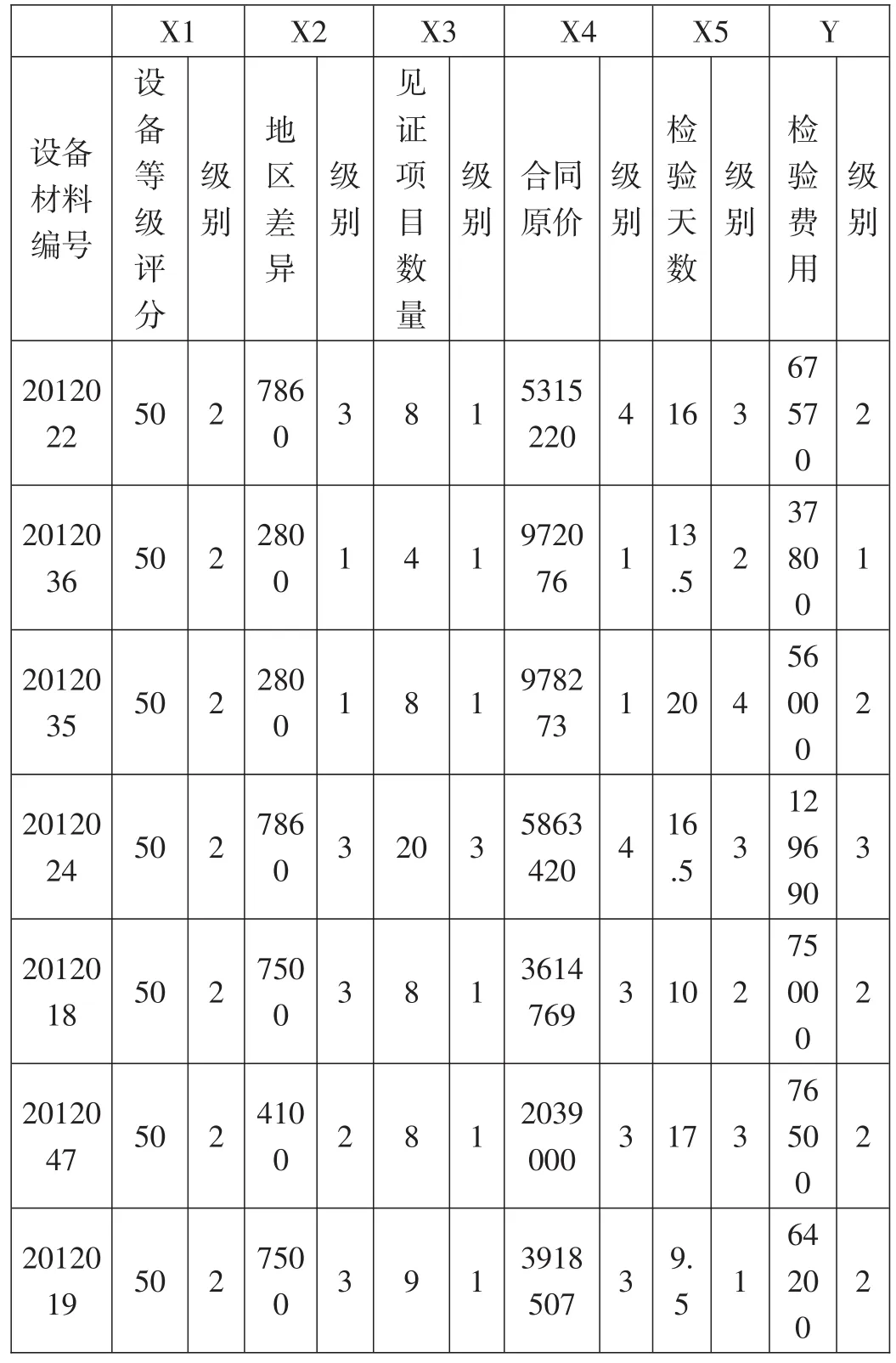
X1合同原价设备材料编号设备等级评分5 0 X4 786 0 5315 220 13 .5 X2 50 280 0 20120 36 9782 73 20120 35 50地区差异20120 18 20120 22 20 5863 420 280 0 16 .5 3614 769 10 786 0 50 X3 20120 47 750 0 20120 24级别2 2 2 2 2 2 2 410 0 50见证项目数量8 4 8 2 0 8 8 9 50 17级别3 1 1 3 3 2 3 X5级别1 1 1 3 1 1 1 9720 76 2039 000 20120 19 750 0 50 3918 507级别4 1 1 4 3 3 3检验天数1 6 9. 5级别3 2 4 3 2 3 1 Y检验费用6 7 57 0 37 80 0 56 00 0 12 96 90 75 00 0 76 50 0 64 20 0级别2 1 2 3 2 2 2
2.3 回归分析
利用SPSS软件进行线性回归分析:
2.3.1 相关性检验
a)第一次分析
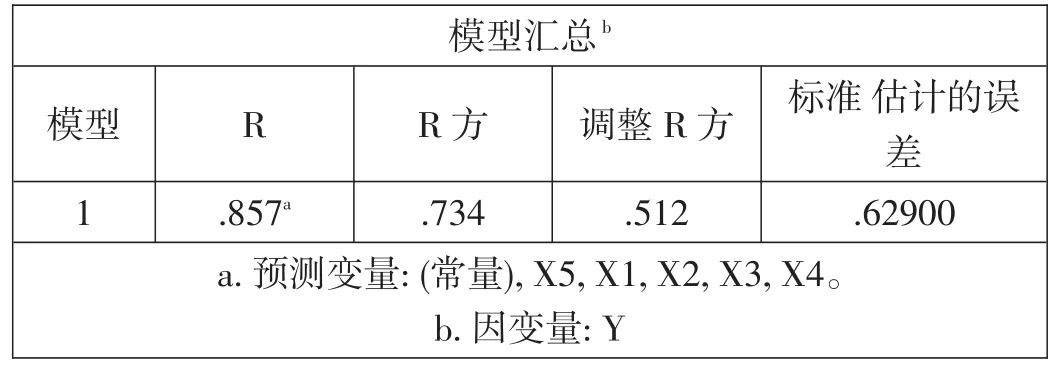
表2 -2 第一次分析模型数据表
通过分析可看出,R值为0.857,R方值为0.734,大于0.5,小于0.8,基本可以接受,说明自变量与因变量之间有相关关系,但是总体相关关系不是十分拟合。
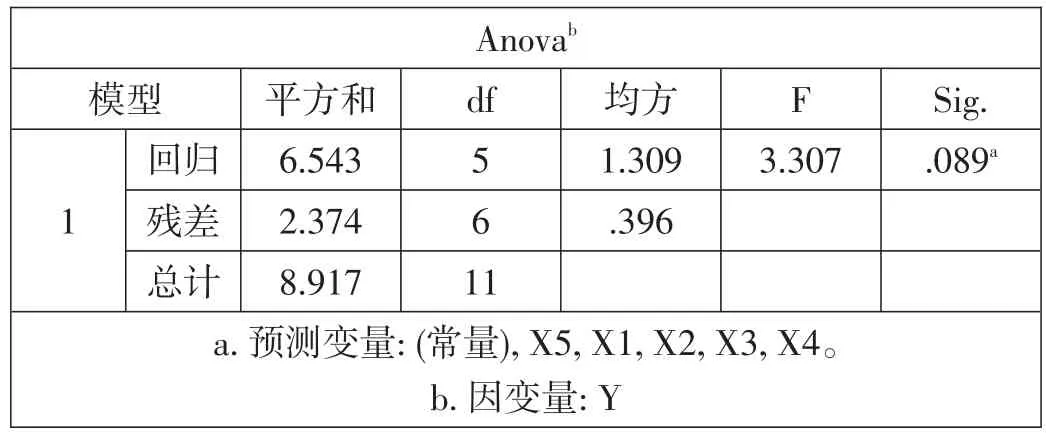
表2 -3 第一次分析方差分析表
根据方差分析表显示,Sig值为0.089,大于0.01,可以看出选取的影响因素,影响较不明显。
b)第二次分析
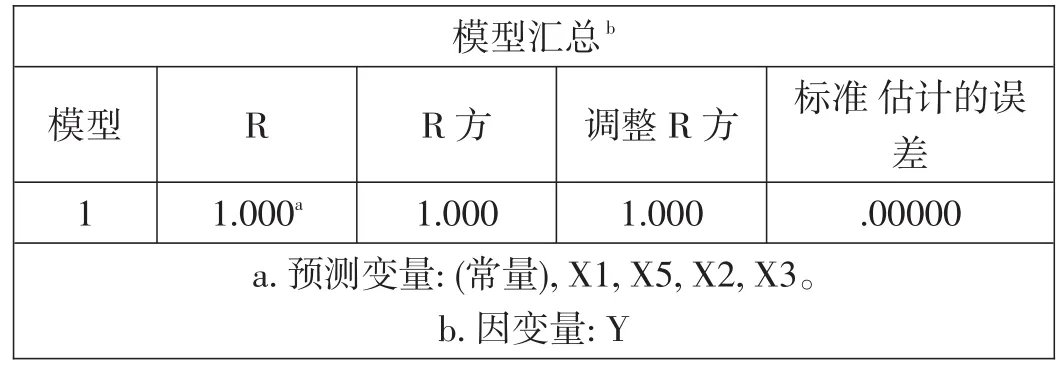
表2 -4 第二次分析模型数据表
第二次分析取消的X4项,可以非常明显的看出,R值和R1值都为1,拟合十分完美。由此可以确定X4于Y值的影响不大,即检验费用和设备、材料采办合同价格用无直接关系。
2.3.2 建立回归模型
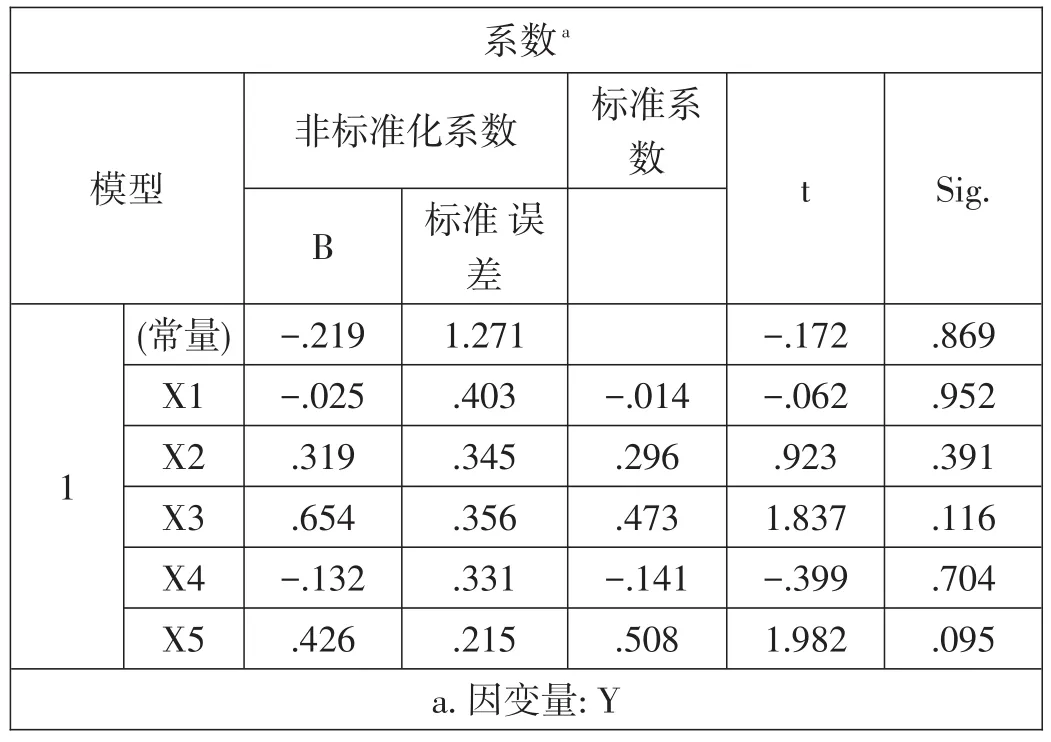
表2 -5 回归系数表
根据回归系数表,建立回归模型:
3 总结
3.1 回归分析结果总结
影响检验费用的因素不止上文中所提到的这5个,因实际情况中,其他的影响因素出现频次较低,所以在此暂不考虑。
通过对检验费用的分析可以看出:
a)合同总价对检验费用影响不是很大。
b)见证项目的系数最大,但考虑到设备材料制造工艺日趋成熟,其检验见证的项目日趋标准化、统一化,除业主特殊指定外,检验见证项目基本上是按照标准执行,其对检验费用的影响有限。
c)地区差异影响因素一项,系数较其他项较少,但其基数较大,且在实际工作中,因采购的设备、材料供应厂商不同、甚至同一设备、材料的原材料产地不同都有可能导致检验过程中在不同地区进行检验,其变化较大,对检验费用的影响也较大。
d)设备等级由专家进行判定,且分级基本固定,可控性不强,即使对检验费用有较大影响,在日常的管理过程中,也较难通过管理手段来调控以达到对检验费用影响的目的,在此不详细展开讨论。
e)检验天数与检验费用关系较为明显,不再赘述。
3.2 增强管理方向
根据上述分析,可以从以下几个方面加强管理,以达到把控检验管理费用的目标:
3.2.1 预先估算,实时监控。
在某项材料设备执行检验前,使用上面得到的公式进行预先估算,并根据ITP对检验见证费用进行分解计划,在设备材料制造进行过程中,对检验见证费用进行实时监控,如产生偏差或在货物尚未交付前就产生了超额的现象,应当及时预警和纠偏,尽量降低检验见证费用增速。但同时应注意保证质量。
3.2.2 提高效率,减少天数
提高检验效率,增加沟通,要求供应商提前准备,减少检验过程中不必要的等待和窝工。减少检验天数将对检验见证费用降低产生明显作用。
3.2.3 减少产品区域变化
在采购合同签订时,指定原材料品牌、生产地,避免因供应商生产过程中原材料供应地分散、生产工厂分散所导致的检验见证地点跨度较大、检验见证过程不能连贯等现象的发生。同等质量条件下优先考虑国产品牌,也可大幅降低检验见证费用。
