计及发车规律的公交车换电站容量优化配置

于德高，邹艳梅中石化天然气川气东送管道分公司

计及发车规律的公交车换电站容量优化配置

于德高，邹艳梅
中石化天然气川气东送管道分公司

由于动力电池换电过程所需时长远小于充电过程、动力电池充电便于统一管理等优点，动力电池换电模式成为电动汽车能量补充的重要方式。本文考虑公交车发车规律，对可就地向动力电池组充电的公交车换电站的容量优化配置展开研究。首先介绍换电站的系统结构，提出平均延迟发车时间的评价指标；然后分析换电站充电以及换电状态的时序仿真模型，计算评价指标；构建以设备年成本为目标函数、换电站规模和平均延迟发车要求为约束的数学模型；采用微分进化算法对数学模型进行求解；最后对算例进行优化配置，计算换电站不同延迟要求下的平均延迟发车时间指标，并对配置结果敏感性进行分析。

公交车；换电站；发车规律；优化配置

1 引言

电动汽车从电网获取电能，相对燃油汽车能有效地减少汽油、柴油的消耗，在效率和环境污染方面都具有相应的优势，因此被视为提高汽车产业竞争力、保证能源安全以及减少碳排放量的重要途径[1]。目前，对电动汽车能源供给设施主要有交流充电桩、充电站和换电站。换电站对于公交车有较好适用性，电池标准化等问题易于解决[2]。目前，国内外对于换电站的研究主要集中在选址规划[3]和优化运行方面[4,5]，另外，在电池数量规划方面也有少量研究[6,7]。鲜有在换电站容量优化配置方面的研究，文献[2]研究了考虑换电服务日可用率和换电服务最大等待时长的容量优化配置。现有文献没有针对公交车特有的发车规律进行换电站容量配置，针对此问题，本文提出了考虑发车规律的公交车发车延迟指标，来评估换电站的服务质量；建立了以年成本为目标函数的优化模型；结合换电站规模以及服务质量指标的约束，得到满足服务质量要求的最优换电站容量配置。

2 换电站典型组成

换电站主要由配电变压器、充电机、动力电池以及一些动力电池更换设备组成：1）配电变压器：将配电网电压等级转换为充电机额定电压等级；2）动力电池充电机：将交流电转换为直流电，为动力电池进行充电；3）动力电池：通过充电机进行充电，为电动公交车提供能量；4）动力电池更换设备：将电动公交车剩余电量不足的动力电池更换为充满电的动力电池。除此之外，换电站还需配备存储室以便存储动力电池和传送设备。

3 计及发车规律的延迟指标

由于公交车特有的发车规律，不同的时间段发车的时间间隔并不相同，因此本文提出平均延迟发车时间指标（Average Delay Departure Time-ADDT）。每个发车时间间隔都会对应一个相应的指标，针对单个发车时间间隔，平均延时发车时间百分比的定义如下：

式中，NEY(t)为t时刻延时出站的公交车数量；Δt为仿真运行时间间隔；NEI(t)为t时刻进站的公交车数量；t0、t1分别为当前发车间隔对应的始终时间。

4 换电站运行状态仿真模型

4.1 动力电池充电仿真模型(如图1所示)

动力电池在充电过程中有三种状态：等待充电、正在充电以及完成充电。首先需要确定第i时段等待充电的动力电池组的数量NBDi：

图1 动力电池充电时序图

式中，NEH(i)为第i时段从电动公交车上更换下来的动力电池组数量。

等待充电的动力电池组数量确定之后，便能计算正在充电和完成充电的动力电池组数量（NBZ(i),NBW(i)）。根据充电机数量的不同，分为两种情况讨论。如果换电站的充电机数量足够，第i时段等待充电的动力电池组NBD(i)将会全部进行充电：

式中，T(i,j)为第j组动力电池在第i时段进行充电所需的充电完成时间。

如果换电站的充电机数量不够充裕，那么第i时段等待充电的动力电池组中只有一部分能够进行充电，剩余的需要等到下一个时段，此时：

式中，Nch为换电站中充电机的数量。

至于没有在第i时段进行充电的部分动力电池，其数量计算如下：

这部分动力电池何时进行充电取决于换电站中充电机的使用情况，假设i’时段为i时段之后第一个充电机富裕，没有全部使用的时段，那么这部分动力电池会在i’时段进行充电：

4.2 动力电池更换仿真模型

图2 动力电池更换时序图

与动力电池状态相似，公交车在整个换电过程中也有三种状态：等待换电、正在换电、完成换电。首先需要确定等待换电的公交车数量：

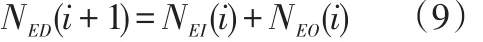
式中，NEI(i)为第i时段到达换电站的公交车数量；NEO(i)为第i时段没有进行换电的公交车数量，其计算过程会在之后介绍。

进行换电的公交车数量与可用的动力电池数量相关，因此需要首先讨论NEH(i+1)与NBA(i)之间的关系，其中NBA(i)的计算如下：

如果换电站中可用的动力电池充足，那么第i+1时段等待换电的公交车将会全部进行换电操作，此时换电（NEH(i+1)）与不换电（NEO(i+1)）的公交车数量计算如下：

如果换电站中可用的动力电池不足，那么只有部分第i+1时段等待换电的公交车会进行换电操作：

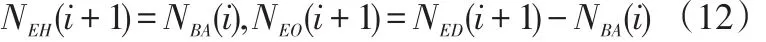
如果上一时段完成换电的公交车全部出战，则完成换电的公交车数量为：

如果上一时段完成换电的公交车尚有部分停留在换电站内，则：

式中，NEJ(i)为换电站第i时段计划出战的公交车数量。

最后确定延时出战的公交车数量：

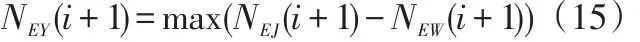
5 换电站容量优化模型

5.1 目标函数

该优化模型以动力电池、充电机以及运行维护费用的年成本为目标函数如下：

CS=CB+CCH（16）

式中，CB为动力电池的年成本；CCH为充电机的年成本；CB和CCH的计算参考文献[2]。

5.2 约束条件

①动力电池和充电机数量约束

假设NBmax为换电站能持有的最大动力电池数量，换电站中，充电机的数量不应大于动力电池的数量：

NB≤NBmax，NCH≤NB-Nbus（17）

式中，Nbus为换电站服务的公交车数量。

②ADDTP指标约束

ADDTP≤ADDTPmax（18）

式中，ADDTPmax为允许的最大平均延迟发车时间百分比。

6 算例分析

6.1 基础数据

根据文献[7]，电动公交车的起始SOC满足正态分布N(0.5， 0.12)。假设换电站内有50辆电动公交车，发车规律数据参照北京市8路电动公交车。动力电池及充电机的参数参考文献[2]。微分进化算法参数：变异因子为0.5；交叉因子为0.4；种群数量为30；迭代次数为60.

6.2 优化结果分析

基于上述基础数据，对换电站的运行情况进行仿真分析，并与文献[2]中方法进行对比分析，表1列出了不同最大延迟出站时长要求下充电机与动力电池的优化配置结果，表2列出了不同延迟出站时长要求下各个发车间隔对应的指标。

表1 充电机与动力电池配置结果

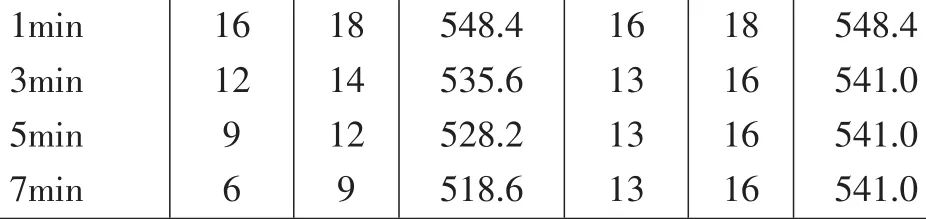
1min1618548.41618548.4 3min1214535.61316541.0 5min912528.21316541.0 7min69518.61316541.0

表2 优化配置结果对应的指标

从表中主要可以看出以下三个结论（1）在最大延迟出站时长为1分钟的要求下，两种方法的配置结果相同。（2）在最大延迟出站时长为3分钟的要求下，本文方法的优化配置结果大于文献[2]中方法的配置结果，这是因为此时在3分钟发车间隔下对应的时间段下，文献[2]中方法对应的发车延迟时长为3.89分钟，大于3分钟，不满足公交车运行实时性的要求；本文方法考虑了发车间隔的约束，优化配置结果对应的发车延迟时长为2.80分钟。（3）由于公交车的运行是时序性的，如果增加7.5分钟发车间隔时间段的延迟时长，必然会增加3分钟发车间隔时间段的延迟时长，为了满足公交车运行实时性的要求，此算例中最大延迟出站时长为5、7分钟的优化配置结果与3分钟的优化配置结果相同。

从上述分析中可以看出，如果不考虑公交车的发车规律进行换电站容量配置，可能会造成某些时间段公交车的发车延迟时间过长，对公交车的实时运行会产生较大影响；本文考虑发车规律的容量配置方法能够弥补上述缺陷，保证公交车的合理运行。

7 结论

本文提出了考虑公交车特性发车规律的换电站容量优化配置方法，通过仿真公交车换电站的充电以及换电操作过程，可以获得充电机以及动力电池各个状态的数量，根据不同换电站对最大延迟出站时长的要求，能够得到相应最优的充电机和动力电池数量配置。在具体的实际应用中，换电站可以根据自身服务的公交车的发车规律以及对延迟时长的要求，计算出最优的配置结果，为换电站的规划建设提供理论依据和技术支持。

[1]肖湘宁，陈征，刘念.可再生能源与电动汽车充放电设施在微电网中的集成模式与关键问题[J].电工技术学报，2013,28(2):1-14.

[2]路欣怡,刘念,汤庆峰,等.计及服务可用性的电动汽车换电站容量优化配置[J].电力系统自动化,2014,14:012.

[3]McPherson C,Richardson J,McLennan O,et al.Planning an electric vehicle battery-switch network for Australia[C]//Australasian Transport Research Forum 2011 Proceedings.2011,12.

[4]张帝，姜久春，张维戈，等.基于遗传算法的电动汽车换电站经济运行[J].电网技术，2013,37(8):2101-2107.

[5]田文奇，和敬涵，姜久春，等.基于自适应变异粒子群算法的电动汽车换电池站充电调度多目标优化[J].电网技术，2012,36 (11):25-29.

[6]刘念，唐霄，段帅，等.考虑动力电池梯次利用的光伏换电站容量优化配置方法[J].中国电机工程学报，2013,33(4):34-44.

[7]Zou F,Liu N,Lu X.Optimal configuration for battery switch stations of electric buses[C]//Transportation Electrification Asia-Pacif⁃ic(ITEC Asia-Pacific),2014 IEEE Conference and Expo.IEEE, 2014:1-5.