光纤法珀压力传感器数据解调及改进算法研究

曹 群，贾平岗，杨 兵，张海瑞，洪应平，熊继军

(中北大学，电子测试技术重点实验室，仪器科学与动态测试教育部重点实验室，山西太原 030051)



光纤法珀压力传感器数据解调及改进算法研究

曹 群，贾平岗，杨 兵，张海瑞，洪应平，熊继军

(中北大学，电子测试技术重点实验室，仪器科学与动态测试教育部重点实验室，山西太原 030051)

基于光纤法珀压力传感器的基本原理，针对相位解调方法中的条纹计数法，提出了优于双峰解调法的多峰平均改进算法，通过滤波实现数据预处理，进而寻找周期内所有数据点的局部极值点，然后根据格拉布斯准则剔除粗大误差，最终得到腔长变化与压力的关系曲线。在此基础上通过MATLAB进行理论仿真，搭建光纤传感压力测试系统并进行了相关实验，利用所设计的解调方法对实验数据进行处理，通过对比分析实验结果可知，改进算法可以明显的抑制应变测量系统误差，提高腔长的稳定性，证实了该改进算法具有较高的可行性。

光纤法珀传感；数据处理；光谱解调；改进算法；多峰计算； MATLAB

0 引言

光纤法布里-珀罗传感器由于其体积小，灵敏度高，不受电磁场和恶劣环境的影响，适合于远程信号处理以及可以复用等众多优点，近几年来成为光纤传感领域的研究热点，在民用基础设施和军事上得到了广泛的应用[1-2]。在光纤法-珀传感测量系统中，腔长解调是整个测量系统的重要组成部分，它直接影响着系统的稳定性和准确性。按照调制解调方法的不同，可以分为强度解调和相位解调两类[3-5]，其中相位解调技术通过对输出光波形的分析来计算应变值，由于其精度高、动态范围大、不易受外界干扰的优点，成为目前较为普遍采用的方法。光纤法珀传感器的相位解调方法主要有条纹计数法、离散腔长变换法、傅里叶变换法以及菲索干涉仪法[6-8]等。条纹计数法中多采用峰-峰法，通过公式计算直接得到腔长，概念明确、结果直观且便于实现，但其准确性由干涉输出条纹的峰值波长准确性决定。任何影响峰值处波长的因素，如光谱的离散采样和峰值计算等环节都将对法布里-珀罗腔腔长求解的准确性造成负面影响，因而这种方法准确率低，并且随着光谱信息周期的增多而带来更多的误差。因此，为了减小在实际测量中的数据误差，提高解调精度，在条纹计数法的基础上提出了一种运算简单且准确度更高的多峰平均改进算法，利用MATLAB进行了理论仿真并搭建了相关实验系统，通过对比分析测试结果，证实了改进算法的可行性与优越性。

1 光纤法珀压力传感器测量原理

光纤法珀压力传感器基于多光束干涉原理，其结构如图1所示。光源发出的入射光通过光纤耦合进入传感器内，在F-P腔体的上下表面来回反射，形成多光束干涉，部分反射光沿着原路返回，相遇后再次发生干涉被光谱仪所接收。干涉信号与腔长L有关，当膜片受到外界压力时会沿着轴向产生形变，导致法珀腔腔长变化，从而引起干涉信号发生变化。通过测量干涉信号的变化则可推导出腔长变化，最终进行解调得到压力信息变化数值，实现压力传感。

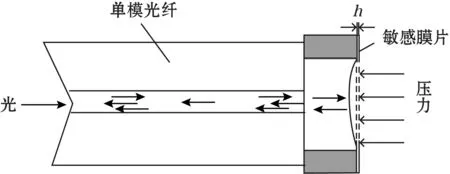
图1 光纤法珀压力传感器结构图

若2个镜面的反射率皆为R，入射光波长与强度分别为λ、I0,在不考虑损耗的情况下根据多光束干涉原理，反射光的光强分布为

(1)

当光纤法-珀腔的2个端面反射率较小时，可以用双光束干涉代替多光束干涉，此时，

(2)

式(1)就可以近似为式(3)

(3)

在小挠度情况下，根据弹性力学原理，硅敏感膜片受到压力后变形情况如公式(4)

(4)

式中：w为硅敏感膜片挠度；p为敏感膜片所受压力；μ为泊松比；E为硅的杨氏模量；h为敏感膜片厚度；R0为膜片半径；r为膜片任意部位的半径。

2 改进解调方法

在采集到光谱数据后，多选用相位解调中的条纹计数法进行解调，使用较多的为双峰法(峰-峰法)，即选取相邻的2个波峰对应的波长值，通过公式计算直接得到腔长

(5)

当φ=2π时，相邻的峰-峰(或谷-谷)间的波长分别为λ1和λ2，则绝对腔长L[9]可以利用下面这个公式来计算

(6)

虽然双峰法能够通过计算直接得到腔长，但其准确性由干涉输出条纹的峰值波长的准确性决定，任何影响峰值处波长的因素，如光谱的离散采样和峰值计算等环节都将对法布里-珀罗腔腔长求解的准确性造成负面影响，因而这种方法准确率低，并且随着光谱信息周期的增多而带来更多的误差。

在实际应用中，不同的波长位置，峰-峰间的间隔相差很大，即信号的周期不一样，如果只选用简单的双峰法，很难得到准确的腔长信息。因此，在双峰法的基础上，我们采用多峰算法进行优化。干涉输出条纹的第m级和第m+q级极大值处对应的光波长分别为λm和λm+q，

(7)

则相应的法珀腔腔长表达式为

(8)

式中q取正整数，按照传感器所得的具体周期数来确定。

该算法主要由滤波处理、极值判断和粗大误差剔除三部分构成，其具体流程如图2所示。

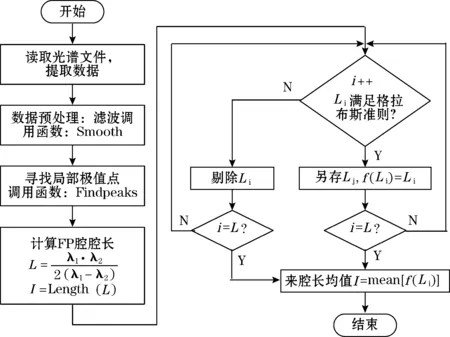
图2 数据处理流程图

在设计的算法中，首先对采集到的光谱数据进行提取，然后进行数据预处理即滤波，接着寻找周期内所有数据点的局部极值点，利用公式计算出法珀腔腔长并根据格拉布斯准则剔除粗大误差，最后对腔长求平均值。

2.1 滤波处理

通过对ENLIGHT软件保存的光谱数据进行二次绘图可发现，在光谱波形中存在许多毛刺，使得整体曲线存在较多的扰动，因此首先需要对光谱数据进行滤波处理，得到相对平滑的曲线以便于后期处理。调用MATLAB自带的Smooth函数，通过移动平均法对数据进行平滑处理，经过滤波后可以得到平滑的曲线，为后续的数据处理提供方便。

2.2 极值判断

在之前的一些处理方法中，常常对采集到的光谱数据进行分组处理。一种方法是根据数据周期设置固定的分组，在单位数组内连续大于零的数值作为波峰数据，按坐标的大小顺序分别放入不同的数组中，然后逐个进行峰值检测；另外一种方法是先设定阈值，然后利用for 语句循环实现动态窗口的分域，循环过程中每遇到连续的非零数据就存入数组中，完成峰值检测后，数组置零并滑向下一组数值，直至完成所有波峰的峰值检测[10]。尽管上述2种方法使用比较普遍，但第一种方法耗时较长，且当外界条件参数不同时采用固定点数进行分组会极大地降低求解精度，第二种方法虽然对于数据的分配更为合理，但在实际处理过程中容易将非波峰数据误判，需要后续的二次处理，使得整体处理的过程复杂化。基于上述经验，本次设计中直接进行局部极值点的寻找，调用MATLAB的Findpeaks函数，逐个查找向量中的波峰，即某一个元素比相邻2个元素的值都大，然后按照每列的搜索顺序标出波峰的值和相对应的横坐标位置。该方法不仅衔接紧密连贯，能够寻找到所有的光谱数据峰值，而且在光谱周期不完全相同时也能很好的运行，不会出现漏点误判的情况，具有良好的通用性。

2.3 粗大误差剔除

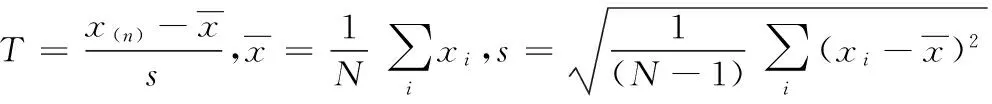
3 算法比较仿真

利用计算机对传感器的输出进行仿真计算，通过两种不同解调方法的对比分析，对改进算法的实际效果得到定性认识。由式(3)可知，光纤F-P腔输出的干涉光强除了与腔长有关外，还是波长λ的函数，当光源光强呈均匀分布时，I0可看成是与波长无关的常数[12]，此时传感器输出的光强在波长坐标轴上呈图3所示的近似余弦分布。

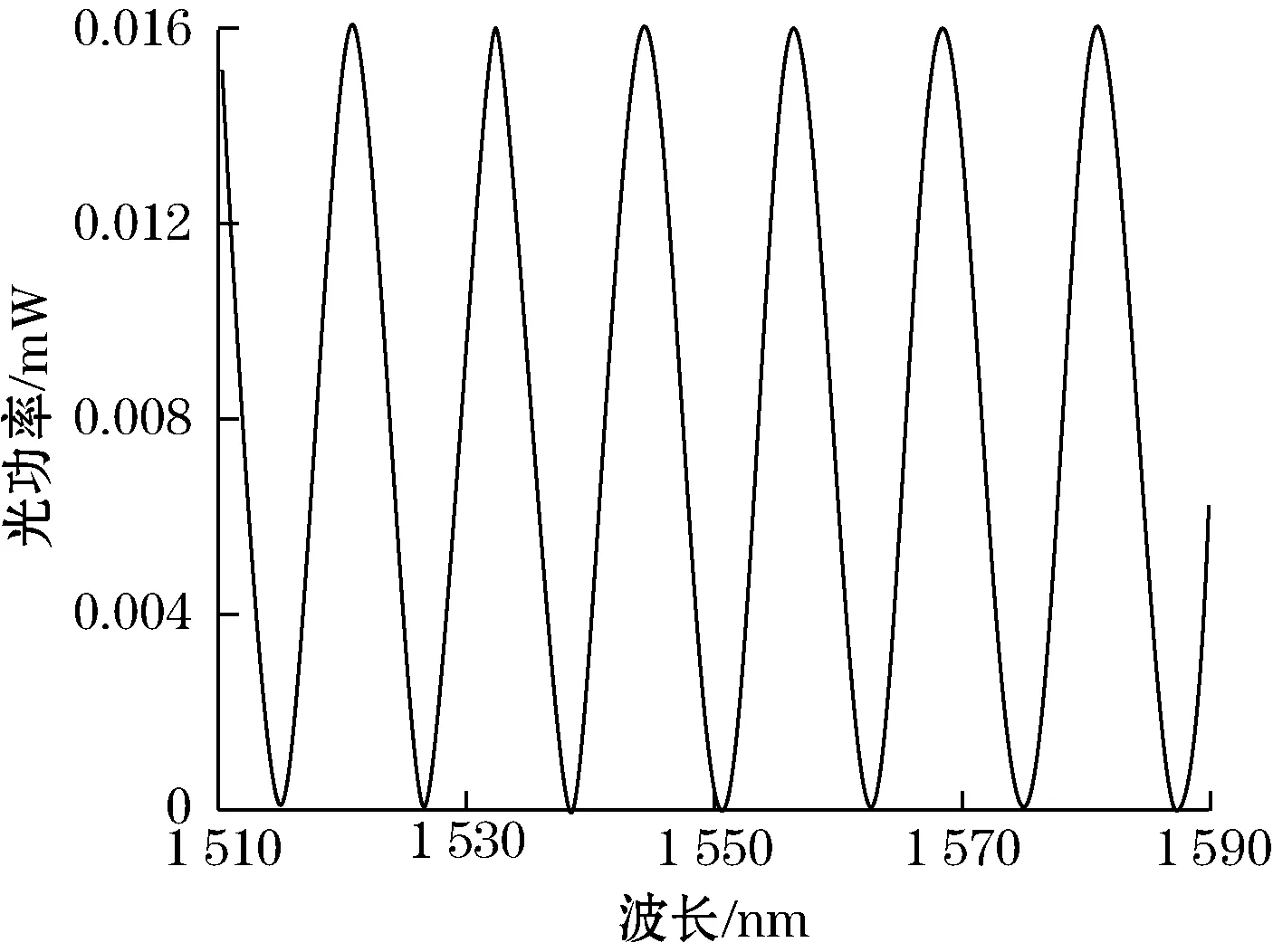
图3 传感器输出的理想光波长分布

假设传感器测得的信号是没有噪声干扰的理想信号，将腔长值代入式(3)就可得出传感器输出光场分布，再根据式(6)或式(8)便可求出其计算腔长值。由于该光纤压力传感器用于测量压力变化，因此根据实际情况进行模拟仿真，令压力从0～300 kPa匀速增加，步进值1 kPa，每次施加压力后根据式(4)得到挠度变化，进而得到此时的腔长L′=L0-ω，L0为传感器初始腔长。再根据所得的腔长值，按照上述方法先求出输出光谱，然后再根据双峰法腔长计算公式或多峰改进算法公式，就可得到传感器计算腔长值与压力理论腔长值之间的关系，如图4所示。其中，双峰法选择光谱图最右边的2个波峰来计算应变(干涉级次比较小)，由于系统误差和干涉级次是平方正比关系，所以这种选择有很好的效果。

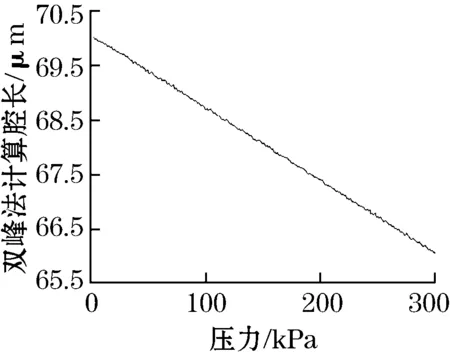
(a)双峰法计算腔长与压力变化曲线

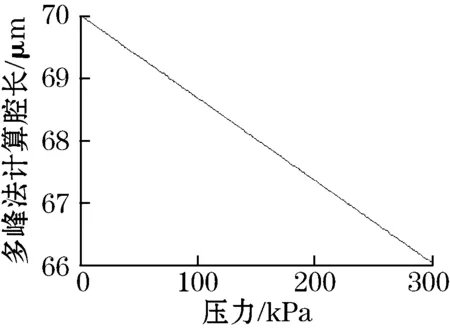
(b)多峰改进法计算腔长与压力变化曲线

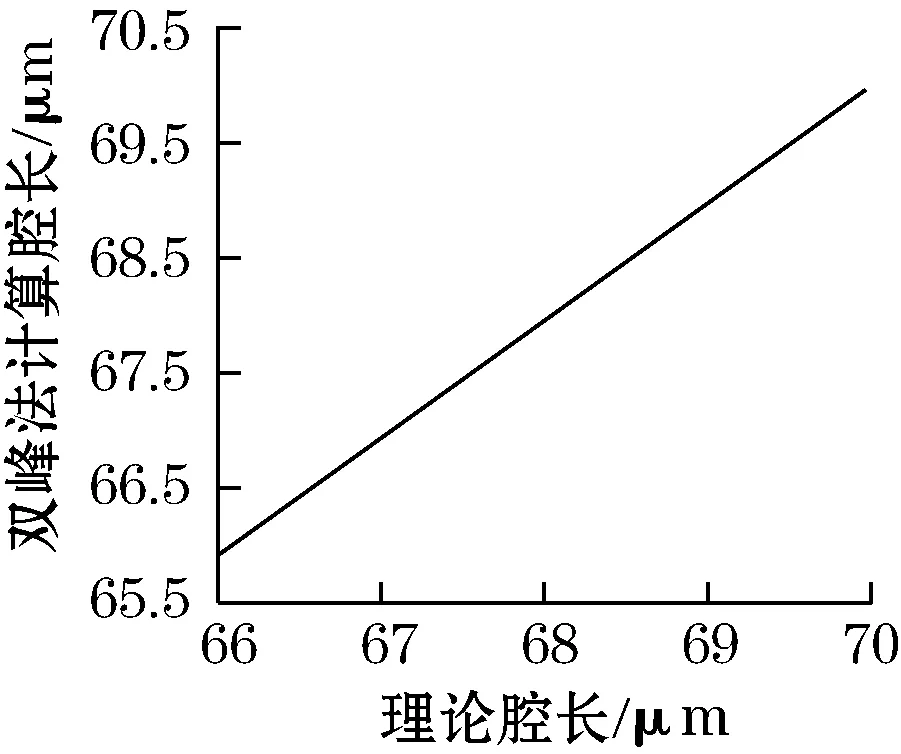
(c)双峰法计算腔长与理论腔长关系曲线

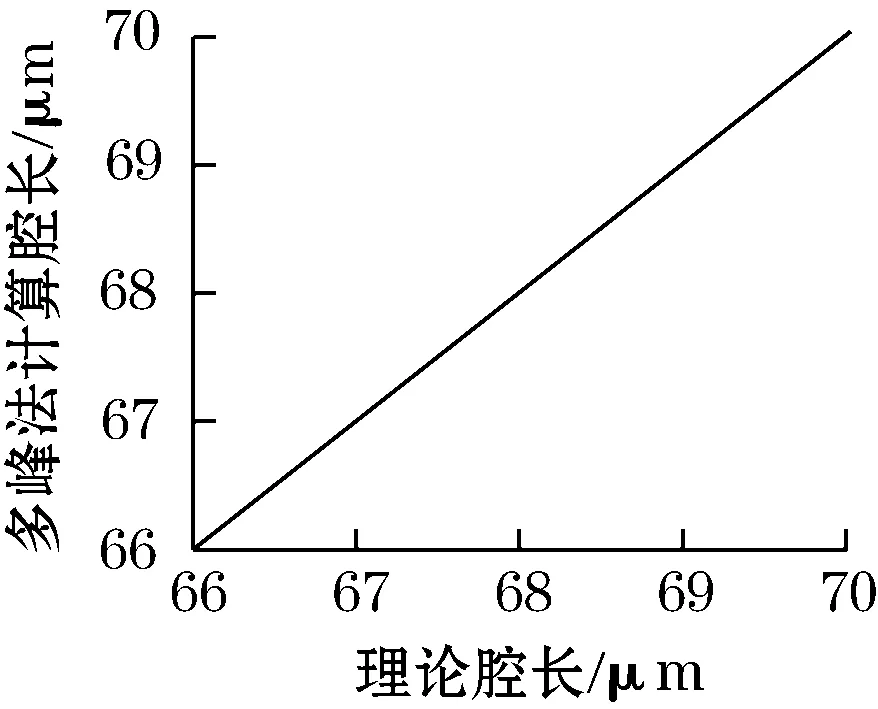
(d)多峰改进法计算腔长与理论腔长关系曲线

从图4可以很直观地看出采用双峰法时，计算腔长值随压力变化存在较为明显的抖动，而多峰平均法的曲线明显平滑了许多，其改进算法的效果较为明显。

4 系统压力加载实验

为了更加真实的对改进算法的效果进行定量的评判，设计了如图5所示的光纤压力传感测试及解调系统。在实验系统中，主要由光纤法珀压力传感元件，温度/压力复合测试设备，光纤光栅解调仪(MOI-sm125)及计算机构成。实验测试时，将传感器放置在密封的真空压力室中，通过压力控制器等量施加压力，引起敏感膜片缓慢产生形变。与此同时，用光谱仪实时记录光纤FP传感器的输出光谱变化，利用计算机分别按双峰算法及多峰改进算法计算出相应的应变值。

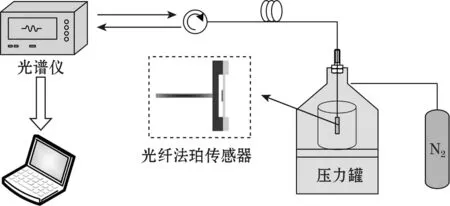
图5 测试系统装置图

在MOI-sm125智能光纤光栅解调仪板中，内置了峰值探测算法，这种峰值探测算法的理想传感器光谱应有0.05～2.0 nm的3 dB带宽，每个形状的中心波长要有至少3～5 dB的对称反差。为了实现更通用的峰值探测，以适应各种光谱形状的传感器，我们不采用板载峰值探测算法，而从智能光纤光栅解调仪中把各通道的光谱数据全部取出在采集客户端进行处理。

在实际测试中，选取的压力范围为0～300 kPa，间隔为20 kPa，压力变化过程中光谱信息会存在一定的时间延迟及条纹波动，因此需要待压力稳定后，再开始记录解调系统输出的波长信息，保存数据后再利用设计好的解调方法进行数据读取与运算。分别利用传统的双峰算法与改进算法对扫描所得峰值进行解调，计算得到不同压力之下法珀腔腔长与压力的变化关系，其中双峰法的解调结果如图6所示。

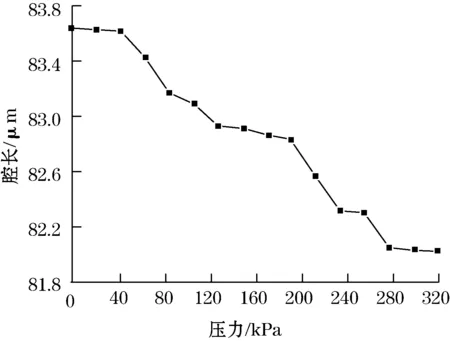
图6 双峰法解调腔长与压力关系曲线

由于实际测试中，会存在加载系统不均匀、胶粘剂等的影响，同时，双峰解调法的准确率较低，并且随着光谱信息周期的增多而产生更多的误差，因此得到的曲线其线性度较差。故在此基础上，利用改进算法对扫描峰值进行解调计算，得到如图7所示的测试结果。

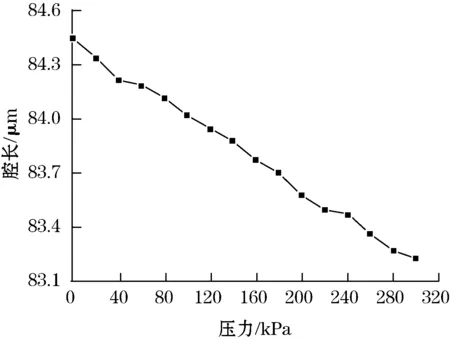
图7 多峰改进算法解调腔长与压力关系曲线

为了定量的得到改进算法与传统算法相对于拟和曲线的偏离程度，在同等条件下，分别对传统双峰算法和改进算法进行多项式Y=A0+A1X+A2X2回归分析，统计出多项式回归系数A0，A1，A2和测量点方差SD如表1所示。由于这两种算法是针对同一组光谱数据的，因而具有很强的可比性。从图6和图7中可以很直观的看出算法B误差小于算法A，将其应变数据经多项式曲线回归后进行定量分析可以看出：

(1) 两条曲线的初始值存在一个差异，这是由于两种算法解调出来的传感器腔长绝对值不同所引起的。

(2) A、B两种算法所测量的应变方差依次减小，这和从两幅应变曲线图上的直观判断完全吻合，这说明了改进算法确实能够很好的的抑制反应测量系统的误差。

表1 两种算法回归分析数据比较

4 结论

在相位解调方法的基础上，提出了能够提高传感器精度的多峰改进算法，通过理论仿真分析和压力加载实验，分别对传统算法和改进算法进行了对比分析，结果表明，多峰改进算法可以明显的抑制应变测量系统的误差，提高法珀腔腔长稳定性，证实了该改进算法具有一定的可行性，在后续的工作中将做进一步的改善与提高。

[1] NGAJIKIN N H,LING L Y,ISMAIL N I,et al.CMOS-MEMS Integration in Micro Fabry Perot Pressure Sensor Fabrication.Jurnal Teknologi,2013,64(3)，83-87.

[2] LI M,WANG M,LI H.Optical MEMS pressure sensor based on Fabry-Perot interferometry.Optics express,2006,14(4):1497-1504.

[3] DAI L,WANG M,CAI D,et al.Optical Fiber Fabry-Pérot Pressure Sensor Based on a Polymer Structure.Photonics Technology Letters,IEEE,2013,25(24):2505-2508.

[4] YU Q,ZHOU X.Pressure sensor based on the fiber-optic extrinsic Fabry-Perot interferometer.Photonic Sensors,2011,1(1):72-83.

[5] LAI C W,YUR J P,LIAO C C,et al.Study on optical fiber pressure sensors with temperature-insensitivity based on Fabry-Pérot interferometry.Recent Patents on Signal Processing,2011,1(1):48-54.

[6] 江小峰,林春,谢海鹤,等.MEMS FP 干涉型压力传感器.红外与激光工程,2014,43(7):2257-2262.

[7] 王代华,刘书信,袁刚,等.并联复用光纤法-珀加速度传感器及解调方法的研究.光学学报,2010 (6):1776-1782.

[8] 葛益娴,王鸣,闫海涛,等.基于相位解调的光纤 MEMS 压力传感器.功能材料与器件学报,2008,14(2):472-475.

[9] 张天地,贺锋涛,周强,等.光纤光栅解调系统的寻峰算法研究.激光技术,2013,37(1):36-39.

[10] 王晓东,王真之,叶庆卫,等.光纤光栅传感系统数据采集与处理技术.仪表技术与传感器,2008(5):47-51.

[11] 张岩.运用格拉布斯准则原理确定公路定额测定中不合理数据.科协论坛:下半月,2009 (2):99-100.

[12] 王宁,朱永,陈伟民,等.光纤法珀应变传感器量化误差及改进算法研究.压电与声光,2002,24(3):251-254.

Study of Improved Algorithm about Data Demodulation of FiberOptic F-P Pressure Sensing System

CAO Qun,JIA Ping-gang,YANG Bing,ZHANG Hai-rui,HONG Ying-ping,XIONG Ji-jun

(Science and Technology on Electronic Test&Measurement Laboratory,Key Laboratory InstrumentationScience&Dynamic Measurement,Ministry of Education,North University of China,Taiyuan 030051,China)

Based on the sensing principle of optical fiber F-P pressure sensor,a kind of multi-peaks average improved algorithm better than peak-peak method was proposed in view of the fringe counting method during phase demodulation method.Data preprocessing was realized through filter function and then the total local extremum points of one cycle were found.According to Grubbs criterion,gross errors were eliminated to obtain the relationship curve between cavity length change and pressure applied.On the basis,theoretical simulation was established using MATLAB and related experiments were taken on after the implementation of optical fiber sensing pressure testing system.By employing the designed demodulation method to complete the comparative analysis of the experimental results,the improved algorithm can significantly inhibit the indeterminacy of strain measurement system and enhance the stability of the cavity length,thus confirming the method of MEMS optical fiber pressure sensing system performs a potential high possibility.

Optical fiber Fabry-Perot sensing;data processing;spectrum demodulation;improved algorithm;multimodal calculation;MATLAB

国家杰出青年科学基金项目(51425505)，青年科学基金项目(51405454)

2015-06-25 收修改稿日期：2015-08-25

TP212

A

1002-1841(2015)12-0015-04

曹群(1990—)，硕士研究生，主要研究方向为光纤压力传感。E-mail:cxqnuc@126.com 熊继军(1971—)，博士，教授，博士生导师，主要研究方向为传感器技术、微纳器件与系统研究。 E-mail:xiongjijun@nuc.edu.cn