基于IPSO的PID参数自整定在流浆箱总压控制中的应用

陈帅帅 赵倩梅 熊智新 胡慕伊

(南京林业大学江苏省制浆造纸科学与技术重点实验室，江苏南京，210037)



·流浆箱总压控制·

基于IPSO的PID参数自整定在流浆箱总压控制中的应用

陈帅帅 赵倩梅 熊智新*胡慕伊

(南京林业大学江苏省制浆造纸科学与技术重点实验室，江苏南京，210037)

稀释水水力式流浆箱的总压控制直接关系到纸张质量的好坏，而传统的PID整定方法精度较低，使用标准粒子群优化算法可以提高精度但是算法敛速度较慢。针对这些问题，采用改进的粒子群优化算法来自整定 PID参数，通过使用非线性递减惯性系数和动态加速因子策略来提高算法的寻优速度及精度。仿真结果表明，用改进的粒子群优化算法整定后的流浆箱总压控制PID有更好的响应速度和鲁棒性。

流浆箱总压；PID自整定；改进粒子群优化算法

(*E-mail: leo_xzx@163.com)

稀释水水力式流浆箱作为目前国际公认的先进型流浆箱，在高速纸机上很常见。由于车速高，纸料从流浆箱喷出到网上定形的时间非常短，而工艺要求纸张定量要均匀一致，其总压的控制就至关重要，它的好坏将直接影响到整个控制系统，关系到流浆箱的喷浆速度和纸张定量分布的均匀程度[1-3]。

流浆箱的压力控制通常采用PID控制，传统的PID参数主要由人工通过经验调整，常用来整定PID参数的方法有临界比例度法、Z-N整定法、衰减曲线法等，这些整定方式比较费时费力，而且不能保证获得最佳性能。粒子群优化算法(Particle Swarm Optimization, PSO)具有简单实用、通用性强等特点，文献[4]将其应用在PID参数整定中取得了一定的效果。但是标准粒子群优化算法也存着容易陷入局部最优、收敛速度慢等缺陷，近年来，国内外学者提出了各种各样的改进方案，使粒子群优化算法的性能得到了很大的提高。总结来说主要是3个方面的改进：改进参数的粒子群优化算法[5]、与其他算法相结合的混合粒子群优化算法[6]、将整个粒子群分成N个相互独立的子群的协同粒子群优化算法[7]。

本文采用一种基于非线性递减惯性系数和动态加速因子的改进参数的粒子群优化算法(Improved Particle Swarm Optimization,IPSO)，并针对稀释水水力式流浆箱总压PID控制器参数自整定模型进行仿真实验，获得了较好的效果。

1 流浆箱总压控制介绍

流浆箱的主要任务是沿着纸机的横幅全宽，均匀稳定地将纸料分布上网，并且保证压力、流量、浓度、速度、纤维定向等因素的均匀和可控。本文中的满流式的稀释水水力式流浆箱的特点是按照纸机车速的要求，利用冲浆泵的输浆压力来调节上网纸料的速度[8]。这种流浆箱的压力和液位没有耦合关系，但是其所对应的纸机车速一般较高，此时总压就成了影响纸张质量的主要因素。只有把总压稳定住，纸张的定量分布才会均匀，生产出的纸张才会满足工艺要求。因此，需要对流浆箱总压进行严格控制，其控制结构如图1所示。

图1 流浆箱总压控制结构图

稀释水水力式流浆箱的喷浆压力由冲浆泵的动压头提供，通过PLC控制冲浆泵的变频器来实现总压控制。总压设定值直接在上位机设定，通过通信接口送给可编程逻辑控制器。冲浆泵送来的浆料经过脉冲衰减器稳定后，以一定的流量送到流浆箱再喷射到网部。冲浆泵由异步电动机拖动，控制器根据总压的设定值和实际测量值，经过一定的处理后，给出4～20 mA的控制信号，通过变频器来控制冲浆泵的转速[9]。

2 粒子群优化算法简介

粒子群优化算法(PSO)由Kennedy和Eberhart于1995年提出。首先在可行解空间中初始化一群粒子，其中每个粒子都代表问题的一个潜在最优解。粒子特征有3个指标：位置、速度和适应度值，其中位置是粒子的主要信息，适应度值反映了粒子的优劣，它是通过适应度函数求出的。粒子在解空间中根据当前的位置和速度运动，通过寻找个体极值Pbest和群体极值Gbest来更新个体位置[10]。

2.1 标准粒子群优化算法

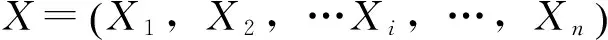
(1)

(2)

其中，ω为惯性权重；d=1,2,…,D；i=1,2,…,n；k为当前迭代次数；Vid为粒子的速度；c1和c2是加速因子，一般取c1=c2=2；r1和r2是分布于[0，1]区间内的随机数。

标准粒子群优化算法参数设置较少，算法简单，但是收敛速度比较慢，而且在后期当自身信息和局部信息占优势时，粒子群容易陷入局部最优解,因此需要改进。粒子群优化算法的流程如图2所示。

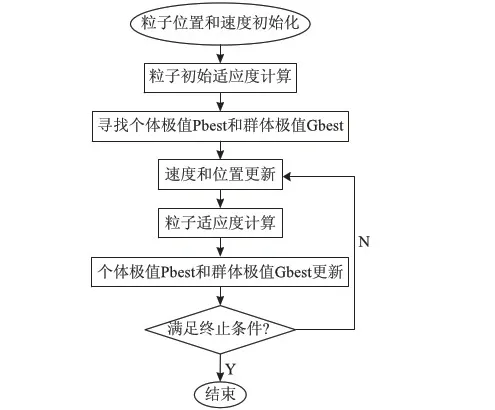
图2 粒子群优化算法流程图

2.2 改进的粒子群优化算法

由于惯性权重ω较大时全局搜索能力较强，较小时则局部搜索能力更强。鉴于算法初期一般希望全局搜索能力较强，以快速搜索到全局最优解，后期则希望局部搜索能力更强，从而达到更加精确的目的，结合文献[11]的改进方法，采用一种非线性递减的方案，其公式为式(4)。

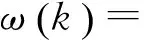
(4)

其中，ωstart和ωend分别表示初始和结束的惯性权重值，Tmax为最大迭代次数，k为当前迭代次数。

同时将加速因子进一步改进，采用c1和c2不相等并且动态调整的方案。为了整体的平衡，c1采用线性递加，c2采用线性递减，并且令c1和c2在同一个区间[cend，cstart]内变化。改进后的公式为式(5)、式(6)。

(5)

(6)

3 PSO算法优化流浆箱PID参数

利用粒子群算法优化PID参数的基本思想就是利用粒子群算法采用实数编码计算相对较快、全局寻优能力较强的特点在一定范围内选出一组最合适的Kp、Ki、Kd，使得控制器的误差性能指标达到最优[12]。

在实际工程中常用的误差性能指标有平方误差积分(ISE)、误差绝对值积分(IAE)、时间乘平方误差积分(ISAE)、时间乘误差绝对值积分(ITAE)等。本文采用的是ITAE指标，这种指标既考虑了静态性能又考虑了动态性能，其公式为(7)。

(7)

对流浆箱总压PID控制器而言，参数共有3个，分别为Kp、Ki、Kd，因此粒子群的维度D=3。而整个控制过程即是适应度函数，控制系统的性能指标ITAE则对应粒子的适应度值。首先由PSO产生或更新粒子群，并将该粒子群中的粒子信息赋予PID参数，然后运行系统得到性能指标，再将得到的性能指标传递给PSO，以此循环直至满足设定的终止条件退出算法,优化过程如图3所示。

图3 PSO优化PID的过程示意图

PSO优化PID的流程如下：

(a)生成并初始化粒子群，随机给出粒子的初始位置和速度，并将初始位置信息赋值给PID参数，运行一次系统得到初始适应度值，由此确定粒子的Pbest和Gbest。

(b)进入循环，按照式(1)和式(2)更新粒子的速度及位置；将每个粒子的当前适应度值跟它所经过的最优位置Pbest的适应值进行比较，如果更好，则将其设置为新的Pbest。

(c)将每个粒子的当前适应值跟整个粒子群的最优位置Gbest的适应值进行比较，如果更好，则将其设置为新的Gbest。

(d)按照式(4)修正惯性权重ω，按照式(5)、式(6)修正c1和c2的值，完成一次迭代。

(e)如果有粒子满足终止条件则退出算法，并得到最优解Gbest，否则返回步骤(b)。以此循环，直到最大迭代次数。

4 仿真实验与分析

根据上述思想，在MATLAB2010b中进行仿真实验。根据文献[3]所述，稀释水水力式流浆箱的总压控制数学模型可以简化为一个一阶惯性加延时的环节，通过阶跃响应作图法求出其模型为式(8)。

(8)

分别利用Z-N整定法、标准PSO优化算法、改进PSO优化算法对PID参数进行整定仿真实验。两种粒子群算法中，粒子群规模均设为100，最大迭代次数均为100次。标准PSO算法中，ω=0.7，c1=c2=2；改进PSO算法中，ω从0.9递减到0.4，cstart=2.5，cend=0.5。3个待优化参数的范围均取[0，10]。

3种方法整定后的参数及性能指标如表1所示。

图4给出了两种粒子群优化算法在总仿真时间为120 s的情况下的ITAE指标变化曲线。从图4可以看出，虽然两种算法最终达到的指标值几乎无差别，但是标准PSO在第68次迭代时才达到最优，而IPSO在第32代就达到了最优，改进粒子群优化算法的收敛速度大大提高。PID参数在优化过程中的变化曲线如图5所示。

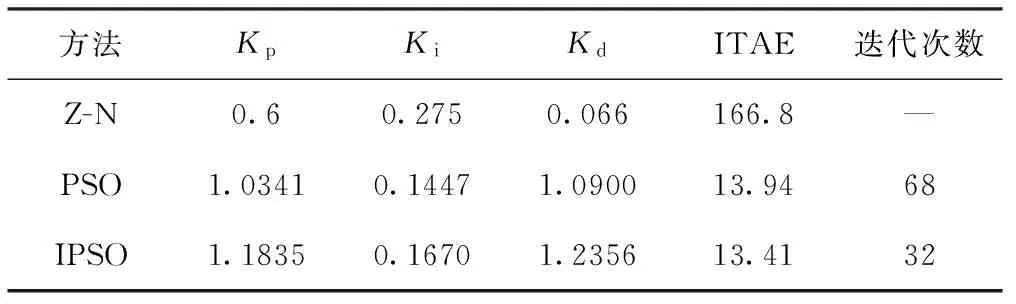
表1 3种方法整定后的PID参数和性能指标

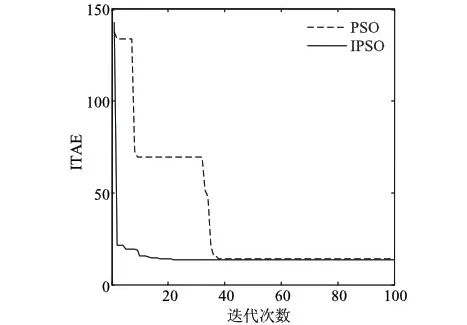
图4 两种粒子群优化的指标变化曲线

图5 IPSO算法的Kp、Ki、Kd优化曲线

图6 不同方法所对应的单位阶跃响应曲线

由图6阶跃响应曲线分析可知，两种PSO算法优化后的PID在超调量和调节时间上都有很大程度的改善；而IPSO算法优化的比标准PSO优化的上升时间减少了14.8%，调节时间也缩短了5.52 s，说明响应速度更快，而且超调量控制在3%以内，显然IPSO算法能够更有效地优化出较好的参数，具有更好的应用前景。

在建模的过程中，由于干扰、噪声和非线性等因素的存在，不可避免地存在着模型失配的问题[13]。

假设模型失配时的传递函数为：

(9)

而控制方案不变，同样加入阶跃扰动，并在100s时给系统加入30%的干扰，Z-N整定法方案、标准PSO优化方案以及改进PSO优化方案的响应曲线如图7所示。从图7可以看出，在面对模型失配以及出现较大干扰的情况时，IPSO优化的PID与Z-N法整定的相比具有更强的鲁棒性，与标准PSO优化的相比响应速度也较快。

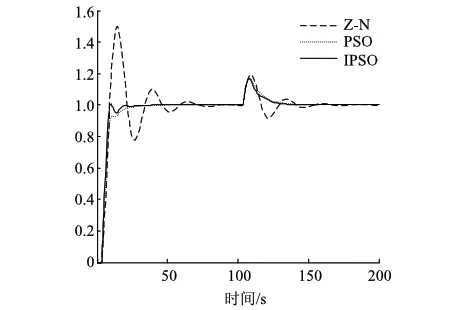
图7 模型失配时的阶跃响应曲线

5 结 论

本文通过对标准粒子群优化算法的改进，提升了粒子群的收敛速度，改善了粒子群优化算法全局搜索和局部搜索之间的平衡关系。针对稀释水水力式流浆箱的总压控制系统进行了PID参数优化仿真实验，结果表明，IPSO优化后的PID比传统方法整定的PID精度更高，控制效果更好；比标准PSO优化算法的收敛速度更快，系统鲁棒性更好。说明IPSO在流浆箱总压PID控制器参数优化中具有很好的效果，对实际生产具有一定的理论指导意义，其应用效果有待于现场实际运行设备的进一步检验。

[1] JIANG Feng-wei.Practical Experience of Headbox Rebuilding[J].China Pulp & Paper, 2009, 28(11): 67.姜丰伟.流浆箱改造与稀释水流浆箱[J].中国造纸, 2009, 28(11): 67.

[2] LIN Mei-chan.Research & Development of the Key Technology of MC Dilution Hydraulic Headbox[J].China Pulp & Paper, 2010, 29(3): 56.林美婵.MC稀释水型水力式流浆箱关键技术的开发[J].中国造纸, 2010, 29(3): 56.

[3] NIU Xu-zhong.Research and Implementation of Dilution Hydraulic Headbox Ontology System[D].Xi’an: Shaanxi University of Science and Technology, 2012.牛绪钟.稀释水水力式流浆箱本体控制系统的研究与实现[D].西安： 陕西科技大学, 2012.

[4] ZHANG Jia-jun.Optimization Parameters of PID Controller Parameters Based on Particle Swarm Optimization[J].Computer Simulation.2010, 27(10): 197.张家俊.基于粒子群算法的PID控制器参数优化研究[J].计算机仿真, 2010, 27(10): 197.

[5] LIU Dao.Research on PID parameters tuning based on improved PSO algorithm[D].Hengyang: University of South China, 2012 刘 道.基于改进粒子群优化算法的PID参数整定研究[D].衡阳： 南华大学, 2012.

[6] LUO Chunsong.Improved Particle Swarm Optimization and its Application in Turning of Controller Parameters[D].Changsha: Hunan University, 2009.罗春松.改进粒子群算法及其在控制器参数整定中的应用[D].长沙: 湖南大学, 2009.

[7] SUI Conghui.The Research of Particle Swarm Optimization Algorithm Improvement[D].Chengdu: Southwest Jiaotong University, 2010.随聪慧.粒子群算法的改进方法研究[D].成都: 西南交通大学, 2010.

[8] LU Qianhe.Papermaking Principle and Engineering.Second Edition.[M].Beijing: China Light Industry Press, 2006.卢谦和.造纸原理与工程[M].2版.北京： 中国轻工业出版社, 2006.

[9] CHEN Hang.Structureand Control of a Hydraulic Headbox with Dilution Water[J].China Pulp & Paper.2013, 32(12): 38.陈 航.稀释水水力式流浆箱结构与控制[J].中国造纸, 2013, 32(12): 38.

[10] SHI Feng, WANG Hui, YU Lei, et al.30 Cases of Intelligent Algorithm Analysis in MATLAB [M].Beijing: Beijing University Press, 2011.史 峰， 王 辉， 郁 磊, 等.MATLAB智能算法30个案例分析[M].北京: 北京航空航天大学出版社, 2011.

[11] Li Hanju, Yi Yang.Human activity recognition based on HMM by improved PSO and event probability sequence[J].Journal of Systems Engineering and Electronics.2013, 24(3): 550.

[12] HU Wei.Self-turning of PID parameters based on improved particle swarm optimization[J].Application Research of Computers, 2012, 29(5): 1791.胡 伟.基于改进粒子群算法的PID控制器参数自整定[J].计算机应用研究, 2012, 29(5): 1791.

(责任编辑：常 青)

Application of the PID Parameters Self-tuning Based on IPSO in Headbox Total Pressure Control

CHEN Shuai-shuai ZHAO Qian-mei XIONG Zhi-xin*HU Mu-yi

(JiangsuProvincialKeyLabofPulpandPaperScienceandTechnology,NanjingForestryUniversity,Nanjing,JiangsuProvince, 210037)

The control of dilution hydraulic headbox total pressure is directly related to the paper’s quality.However, the accuracy of traditional PID turning is low, while the standard particle swarm optimization algorithm(PSO) could improve the accuracy but it had a disadvantage of slow convergence speed.Aiming at those problems, an improved particle swarm optimization algorithm(IPSO) was adopted to self-tune PID parameters in this paper.The speed and accuracy of optimization were improved by using the nonlinear decreasing inertia coefficient and dynamic acceleration factors.Simulation results showed that the headbox total pressure PID controller turned by IPSO algorithm had a better response speed and robustness.

headbox total pressure; PID self-turning； improved particle swarm optimization

陈帅帅先生，在读硕士研究生；研究方向：制浆造纸过程控制与信息智能处理。

2015-05-19(修改稿)

TS736

A

10.11980/j.issn.0254-508X.2015.11.008

*通信作者：熊智新先生，E-mail:leo_xzx@163.com。