目标移位安全区约束的道路D-P化简优化方法

李 国 辉，龙 毅*，许 文 帅，周 侗，高 朝

(1.南京师范大学地理科学学院，江苏 南京 210023；2.常州市基础地理勘测中心，江苏 常州 213003；3.南通大学地理科学学院，江苏 南通 226007)



目标移位安全区约束的道路D-P化简优化方法

李 国 辉1，龙 毅1*，许 文 帅2，周 侗3，高 朝1

(1.南京师范大学地理科学学院，江苏 南京 210023；2.常州市基础地理勘测中心，江苏 常州 213003；3.南通大学地理科学学院，江苏 南通 226007)

针对道路化简产生的与建筑物空间关系不一致问题，以道路与建筑物要素的关联关系为出发点，构建道路的目标移位安全区，在此基础上对D-P化简算法进行改善，提出一种以道路目标移位安全区为约束的D-P化简优化算法，在化简道路曲线的同时保证化简后道路曲线不与邻近建筑物产生空间冲突。选取1:10 000的建筑物与道路数据对多种目标比例尺的化简操作进行实验，结果表明该方法可有效保持道路与建筑物间的空间关系。

目标移位安全区；道路；建筑物；D-P化简；优化方法

0 引言

地图制图综合中，常需对道路数据进行化简[1]。早期针对曲线化简算法的研究取得了丰富的成果，方法也比较成熟，典型的有Douglas-Peucker法(D-P法)、Lang法、Li-Openshaw法、垂距法、光栅法等[2-4]，其中D-P法是一种从全局出发的经典化简算法，通过递归逐步舍弃次要点以达到化简目的[5]，在道路数据的化简中应用广泛[1]。建筑物与道路之间有着显著的空间依赖性和语义依存性，建筑物多沿道路两侧布局，两要素贴合紧密[6]，因此道路的化简操作需要协同考虑建筑物的空间布局。传统的基于道路单要素化简可能导致道路与建筑物的空间冲突，比如道路与建筑物几何上相互压盖，严重情况下建筑物可能因为道路弯曲段的化简而从道路的一侧越到另一侧，产生方位冲突。

道路与建筑物冲突处理主要有移位道路与移位建筑物两种方式，其选择取决于数据的定位精度和具体的应用背景。已有的冲突处理方式主要针对地图比例尺缩小道路变宽或者道路符号化后产生的拓扑关系冲突或视觉邻近冲突情况[7-12]，此时根据要素的优先级和精度大小，多采用移位建筑物的方式以保证具有较高优先级的道路精度。而对于诸如风景名胜区、动植物园或建筑物专题图等建筑物重要性高于道路的情况，综合过程中建筑物优先级往往高于道路[13]，此时宜保证建筑物不动而调整道路；且在数据来源、比例尺相同原始数据精度相似的情况下，化简后的道路准确性和精度要低于建筑物[13]，移位建筑物的方式容易导致几何精度进一步降低。

道路图形的协同化简既是对自身几何信息细节的约简，又是对两要素空间、结构关系等进行保持和维护的过程，考虑到道路与建筑物之间具有天然的地理关联性，仅通过道路单要素的化简无法保证化简后的道路与建筑物达到一致化的效果。本文根据道路与建筑物的联合CD-TIN探测双要素之间空间邻近关系，在此基础上构建道路的目标移位安全区(Security Area of Object Displacement,SAOD)，以目标移位安全区约束道路曲线的化简，有效避免了双要素之间因为道路化简而产生的空间冲突。

1 问题描述

1.1 相关概念

(1)路段。路段是路网中被道路交叉点分隔而成的道路曲线段，是一条完整道路的一部分。在化简过程中，由于道路交叉点有着特殊的地理指示作用，精度要求高，因此以路段作为构建目标移位安全区进行协同约束化简的基本单位，可以利用D-P化简保留首末点的特性强行保留道路交叉点。

(2)双要素。要素是从几何和语义角度划分的一类地理目标的集合，如道路目标的集合即为道路要素。由于本文主要研究道路与建筑物间的空间关系及其协同操作，因此下文提及的双要素特指道路与建筑物两个要素。

1.2 基本思路

地图上建筑物应位于道路两侧，道路化简产生的双要素冲突往往是与邻近的建筑物相交或越过邻近建筑物而导致的空间冲突。解决此冲突直接而有效的方式就是避免空间冲突的产生，即改变道路化简方法，将道路的化简结果控制在邻近建筑物所约束的空间范围内，该空间范围即目标移位安全区。由于建筑物成组分布且形态变化较大，与道路之间的邻近程度也不同，无法通过缓冲区等方法获得定宽的目标移位安全区，而CD-TIN是一种从全局角度构建的空间结构，通过三角形边的连接关系探测道路与建筑物目标间的邻近关系，方便构建道路的目标移位安全区。D-P算法作为曲线化简的经典算法，在道路的化简过程中应用广泛，且由于该算法是一种以逐步递归由粗到精的方式寻找曲线的特征点，因此可以借鉴该特点，对导致空间冲突的局部线段通过增加递归程度逐步消除冲突。

2 双要素协同的SAOD提取

2.1 CD-TIN特征三角形分类

由于Delaunay三角网结构具有很好的空间关系表达能力，通过构建双要素联合CD-TIN可以有效探测要素之间的邻近关系。三角形类型特征是判断成组三角形组合模式的基础，也是进行SAOD提取的必要条件。根据三角形顶点所在的目标类型及顶点之间邻接关系的不同，将CD-TIN三角形分为不同的类型，表1为与道路移位安全区提取相关的三角形分类及其形式化描述。需要指出的是，同一个三角形在不同路段中类型可能不同，因此三角形类别必须针对特定的路段。

表1 三角形分类及其详细说明

Table 1 Classification and description of triangles

三角形类型形式化描述图形路端三角形(P0∈Δt∧P1∈Δt)∨(PN-2∈Δt∧PN-1∈Δt)图1△A1/△A2桥接三角形DRL+DSL=2∨(DRL=2∧DSL=1)图1△B1/△B2/△B3/△B4路内三角形DRL=1∧DSL=0图1△C分叉三角形DRL=3∧DSL=0图1△D

定义当前路段从起点到终点编号P0、P1、P2、…、PN-1共N个点，对于三角网中任意给定的三角形t(v1,v2,v3)(简称为△t，其中v1、v2、v3为3个顶点)，Pk∈Δt表示路段的第k个点是△t中的一个顶点，DRL表示△t的3个顶点所在不同路段的个数，DSL表示△t的3个顶点中在建筑物上的个数。图1中的粗实线为当前路段，三角形针对该路段进行类型判别。

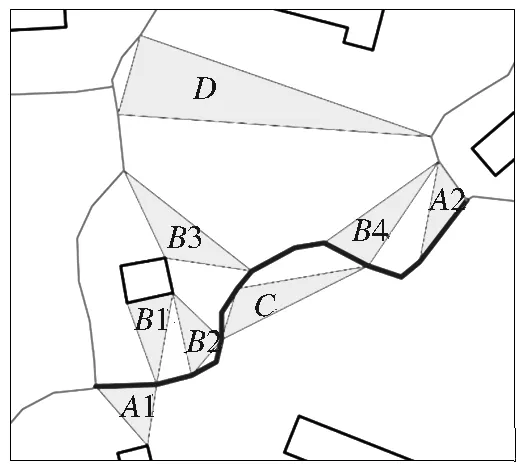
图1 CD-TIN三角形分类示意

Fig.1 Classification of CD-TIN triangles

2.2 SAOD提取

SAOD构建过程中，首先提取与当前路段直接相连的所有三角形并存于集合T，其次根据T中三角形的不同类型采用如下规则提取新的多边形以构建SAOD。新建集合S用于存放处理后的三角形或四边形，具体构建规则如下(定义center(v1,v2)表示v1和v2点的中点，center(t)表示△t的中点)。

规则1：对于路端三角形t(v1,v2,v3)，设v1和v2位于当前路段的起始点上；若v3位于建筑物上，如图2a中三角形t1，则将△t存入S中；若v3在另外一条路段上，如图2a中三角形t2，则重新构建三角形t(v1,v2,center(v2,v3))存入S；特殊情况下，若v3位于当前路段上，则按照路内三角形的处理规则对△t进行处理。

规则2：对于接桥三角形t(v1,v2,v3)，设v1点位于当前路段上；若v1位于路段的起点或终点，且v2和v3都不在当前路段上，则该三角形不参与构建SAOD，直接删除；若只有一个点位于其他路段上(设该点为v3)，另外一点位于建筑物或当前路段上，如图2b中三角形t1，则构建三角形t(v1,v2,center(v1,v3))存入S；若v2和v3两点位于除当前路段外的同一路段上，如图2b中三角形t2，则构建三角形t(v1,center(v1,v2),center(v1,v3))存入S；若△t中所有点位于建筑物和当前路段上，如图2b中三角形t3，则直接将△t存入S中即可。

规则3：路内三角形t(v1,v2,v3)与其他任何目标无联系，如图2c中三角形t1，整个三角形都属于路段的SAOD，只需要将△t完整存入S即可。

规则4：分叉三角形t(v1,v2,v3)被3条不同路段共用，如图2d中三角形t1，设v1点位于当前路段上，v2、v3分别位于另两条路段上，则构建多边形t(v1,center(v1,v2),center(t),center(v1,v3))存入S。

对集合T中的所有三角形按照上述规则处理后，集合S就存放了组成当前路段的SAOD所需的几何体，只需要将S中的几何体依次合并成一个统一的多边形，如图3所示，粗实线表示当前路段，虚线包围的阴影区域即为该路段的SAOD。

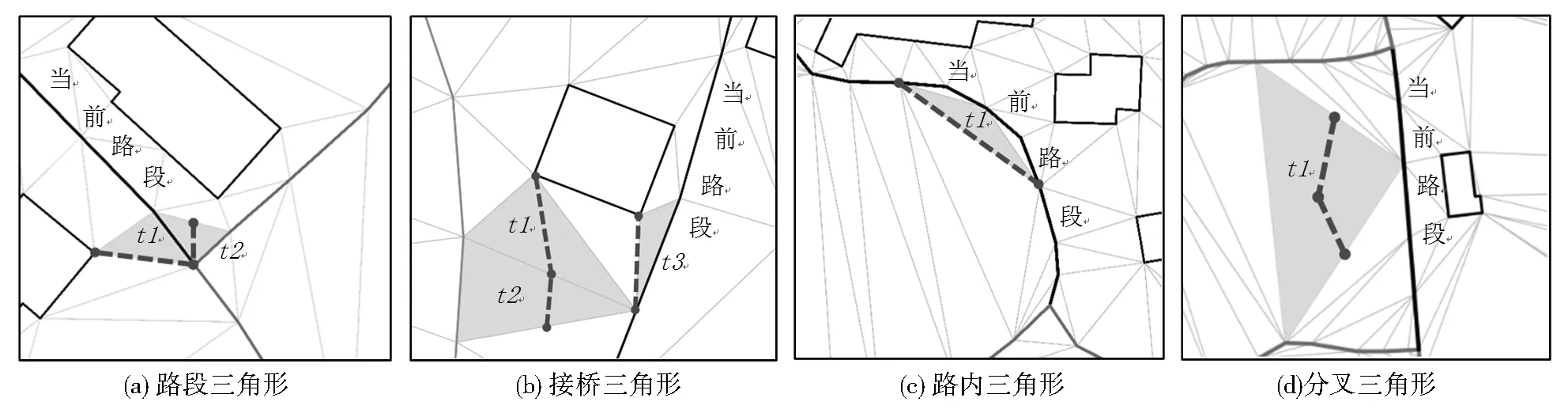
图2 不同条件下SAOD提取过程示意

Fig.2 Diagram of SAOD extraction process under various conditions

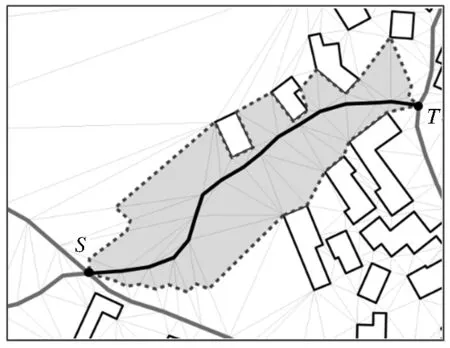
图3 一条路段的SAOD

Fig.3 The SAOD of one road fragment

3 D-P化简优化方法

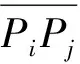
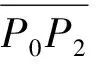
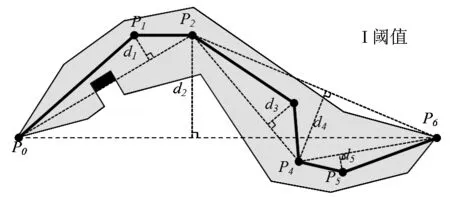
图4 D-P优化算法示意

Fig.4 Diagram of optimized D-P simplification

4 实验与分析

在Eclipse 3.7环境下利用Java语言对提出的方案进行实验和分析。数据选取1∶10 000庐山地区部分道路与建筑物数据，如图5a所示，其中建筑物335个，路段67个，道路总点数为913个，构建的SAOD如图5b所示。以1∶25 000作为化简的目标比例尺，图上距离3 mm作为最小可视范围，可得D-P化简阈值为7.5 m。图6显示了传统D-P化简结果和以SAOD为约束的D-P化简结果的叠加图，可以看出，传统的化简方法导致道路与建筑物相交的情况较多，而以SAOD为约束化简方法有效避免了双要素之间的空间冲突，保持了双要素间的空间关系一致性，化简结果较好。

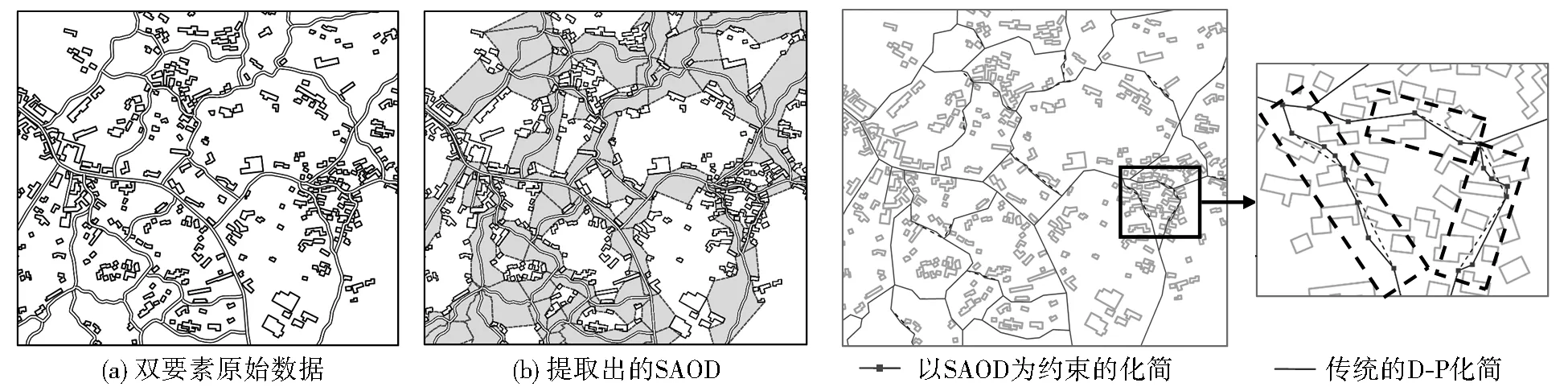
图5 双要素原始数据及其SAOD 图6 两种化简方式的叠加示意(1∶25 000)

Fig.5 Original data of two feature and their SAOD Fig.6 Diagram of two simplification methods

为进一步检验方法在跨越多比例尺下的可行性，对经典D-P化简(简称“方法1”)和SAOD约束化简(简称“方法2”)两种方式4种目标比例尺下的多组化简结果进行统计(表2)。定义化简率为道路化简后被删除的总点数与化简前的总点数的百分比，可见化简率是评价化简程度的重要标准。图7是两种方法在不同比例尺下的化简率。

表2 道路化简数据统计

Table 2 Statistical data of road simplification

根据表2和图7可得如下结论：1)随着比例尺跨度逐渐变大，利用方法1对道路单要素进行化简出现的两要素间空间冲突数量逐渐增多；方法2由于将曲线严格控制在安全范围内，因而有效避免了空间冲突的产生。2)从化简程度的角度看，本文提出的方法在比例尺跨度较小情况下的化简效果较好，当比例尺跨度逐渐变大时，方法2的化简率提升幅度逐渐减小，与方法1的化简率差值逐渐变大。可行的解决办法是化简道路之前先选取道路与建筑物,将次要道路和建筑物删除。此外，单要素化简时个别目标之间出现相交的情况(如图8a以道路与岛屿要素为例)，在利用目标移位安全区进行约束化简时也可以解决(如图8b)。由此可见，本文提出的方法在处理要素内部的空间冲突时也具有一定的可行性。

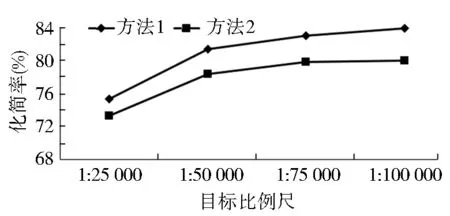
图7 化简率走势

Fig.7 Trend of simplification rate

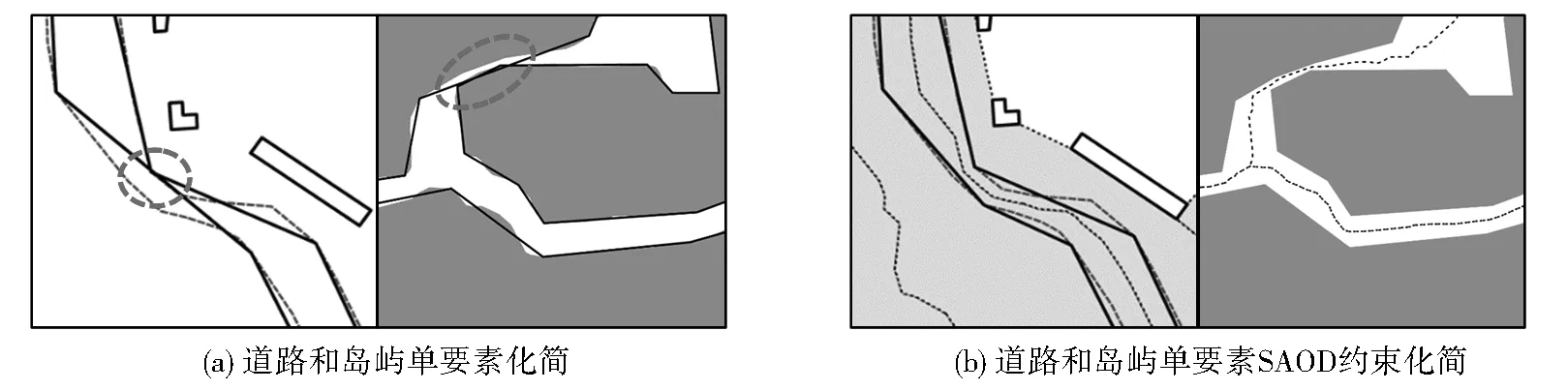
图8 D-P优化化简方法在单要素内部冲突处理的作用

Fig.8 Role of this method in handing feature internal conflict

5 结论

在经典的D-P化简算法的基础之上，通过构建道路与建筑物双要素的CD-TIN提取道路的目标移位安全区，设计出D-P化简的优化方法，在有效化简道路曲线的同时避免了道路与建筑物之间可能的空间冲突，同时该方法在处理要素内部的空间冲突时也有一定的可行性。需要说明的是,以SAOD为约束的D-P优化化简算法在比例尺跨度过大时会导致化简率提升幅度逐渐放缓，且地图比例尺缩小后，符号化后的道路宽度也随之增大，可能出现原始道路与建筑物之间产生空间冲突需要移位建筑物的情况，因此对于比例尺跨度较大且化简率要求高的操作的适用性较低。在今后研究中将进一步探讨如何在保证道路与建筑物空间关系一致性的同时不损耗道路的化简率。

[1] 李少梅,安晓亚,孙群,等.道路数据综合的融合算法研究[J].测绘科学,2009(5):11-13.

[2] 张传明,潘懋,吴焕萍,等.保持拓扑一致性的等高线化简算法研究[J].北京大学学报(自然科学版),2007,43(2):216-222.

[3] 陈轶,彭认灿,郑义东,等.基于 Douglas 双侧多叉树的曲线综合算法研究[J].测绘学报,2010,39(3):310-315.

[4] OPHEIM H.Fast data reduction of a digitized curve[J].Geo-processing,1982,2:33-40.

[5] DOUGLAS D H,PEUCKER T K.Algorithms for the reduction of the number of points required to represent a digitized line or its caricature[J].Cartographica:The International Journal for Geographic Information and Geo-visualization,1973,10(2):112-122.

[6] 陈文瀚.地图道路与居民地协同综合方法研究[D].南京:南京师范大学,2011.

[7] 吴小芳,杜清运,徐智勇.多层次移位原则的道路与建筑物空间冲突处理[J].测绘学报,2010,39(6):649-654.

[8] 艾廷华.基于场论分析的建筑物群的移位[J].测绘学报,2004,33(1):89-94.

[9] 周启,艾廷华,张翔.面向多重空间冲突解决的移位场模型[J].测绘学报,2013,42(4):615-620.

[10] 侯璇,武芳,刘芳,等.基于弹性力学思想的居民地点群目标位移模型[J].测绘科学,2005,30(2):44-47.

[11] 何津,费立凡.解决图形冲突的受限变形所涉及的数学原则:以道路与建筑物的关系为例[J].武汉大学学报(信息科学版),2007,32(4):326-330.

[12] 费立凡,何津.解决街道与建筑物图形冲突的移位模型研究[J].武汉大学学报(信息科学版),2007,32(6):540-543.

[13] 王家耀.地图学原理与方法[M].北京:科学出版社,2006.

An Optimized Douglas-Peucker Method of Road Simplification Based on SAOD Constraints

LI Guo-hui1,LONG Yi1,XU Wen-shuai2,ZHOU Tong3,GAO Zhao1

(1.CollegeofGeographicScience,NanjingNormalUniversity,Nanjing210023;2.BasicGeographicSurveyingCenterofChangzhou,Changzhou213003;3.SchoolofGeographicScience,NantongUniversity,Nantong226007,China)

This paper presents an optimized Douglas-Peucker(D-P)algorithm to simplify roads curve which is focus on the inconsistency between simplified roads and buildings.In order to make sure the simplified roads do not cross the nearby buildings,this paper puts forward a concept named Security Area of Object Displacement(SAOD)which is extracted by Delaunay Triangulation(DT)of two features.The SAOD of a road is decided by the nearby buildings.The simplification ensure simplified road in a certain range by changing the recursion condition of the D-P algorithm.That is to say,the method not only can simplify the curve,but also can maintain consistency of spatial relations.Several experiments were taken to test this method.The results showed that the method can effectively avoid the conflicts between simplified roads and buildings.

SAOD;road;buildings;D-P simplification;optimized method

2014-11-26；

2015-01-28

国家自然科学基金项目(41171350、41271449、41301514)；江苏省高校自然科学研究项目(13KJB170020)

李国辉(1989-)，男，硕士研究生，主要研究方向为地图自动综合。 *通讯作者E-mail：longyi@njnu.edu.cn

10.3969/j.issn.1672-0504.2015.03.004

P208

A

1672-0504(2015)03-0017-05