车辆非线性8-DOF模型的简化分析

刘 刚，王常乐，郑凯锋，王文竹

(1.沈阳航空航天大学 机电工程学院，辽宁 沈阳 110136；2. 中国北方车辆研究所，北京 100072)



车辆非线性8-DOF模型的简化分析

刘 刚1，王常乐1，郑凯锋2，王文竹1

(1.沈阳航空航天大学 机电工程学院，辽宁 沈阳 110136；2. 中国北方车辆研究所，北京 100072)

在对车辆侧向动力学的研究中，多采用非线性8自由度(8-DOF)模型，但车辆主要的4个自由度(纵向、侧向、横摆和侧倾)运动微分方程在使用中常需要不同程度的简化，针对这些简化形式，建立了完整的非线性8-DOF模型，对比了各类简化项对整车动力学响应特性的影响，最后给出一种合理的最简形式。

车辆工程；非线性8-DOF模型；简化分析；最简形式

车辆侧向动力学模型是研究车辆操纵稳定性的基础。由于研究的侧重点不同，模型的形式和复杂程度存在较大差异。一个能够较为全面体现车辆侧向动力学特性的模型应该具有纵向、侧向、横摆、侧倾这4个自由度，同时应考虑载荷转移和轮胎非线性对模型精度的影响。具有纵向、侧向、横摆、侧倾及4个车轮旋转的非线性8自由度(8-DOF)模型很好的体现了车辆侧向动力学特性[1-7]。但是，在非线性8-DOF模型使用中，车辆的纵向、侧向、横摆和侧倾4个自由度运动微分方程有着较多的简化形式。文献[1-7]假设车身侧倾很小；文献[2]忽略了簧载质量惯性积的影响；已有文献部分方程中忽略了侧倾角速度或(和)侧倾角加速度的影响；忽略了非簧载质量产生的力矩对纵向、侧向及横摆运动的影响；而文献[6-7]中有着更多的简化。针对以上问题，研究了不同的简化模型对整车操纵稳定性分析的影响，并给出侧重操纵稳定性某一方面分析时所需的最简模型。

1 车辆非线性8-DOF动力学模型

利用拉格朗日方法推导车辆纵向、侧向、横摆以及车身侧倾运动微分方程，可将整车分为3个部分：具有侧倾自由度的簧载质量(车身)和不发生侧倾的非簧载质量，其中非簧质量由前非簧载质量(前悬架和前车轮)和后非簧载质量(后悬架和后车轮)组成。另外需要建立3个符合右手定则的坐标系：地面参考坐标系G、车辆非簧质量运动参考坐标系A、簧载质量运动参考坐标系B。将过簧载质量质心的垂线与侧倾轴的交点定义为侧倾中心，并记为点O，坐标系A和B的原点与O点重合，坐标系A相对于地面参考系G有一个横摆转角ψ、坐标系B相对于A有一个转角φ，即车身侧倾角，各坐标系的正方向如图1。

参照文献[8]列写出车辆的动能、势能和散耗能方程，并将其代入到特殊形式的拉格朗日方程中[9]，最后进行简化推导便可得到完整的车辆的纵向、侧向、横摆和侧倾运动微分方程。

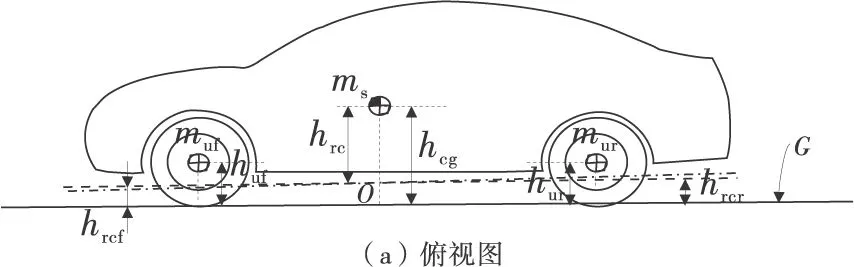
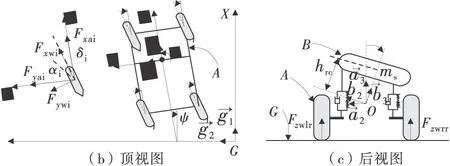
图1 车辆8-DOF模型简图

1.1 纵向动力学方程

在不考虑风阻的情况下，车辆的纵向运动微分方程如式(1)。

(1)

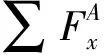
1.2 侧向动力学方程

(2)

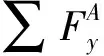
1.3 横摆动力学方程

(3)

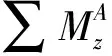
1.4 侧倾动力学方程

(4)

式中：整车侧倾转动惯量Ixx=Ixxs+mshrc，kg·m2；Ixxs为非簧载质量绕其自身中心的侧倾转动惯量，kg·m2。

1.5 车轮转动动力学方程

如果把驱动力和制动直接以力矩的方法施加到车轮上，则车轮的转动微分方程可写为：

(5)

式中：ωwi为车轮的转动角速度，rad/s；Iw为车轮的转动惯量，kg·m2；Twdi为车轮的驱动力矩，N·m；Twbi为车轮的制动力矩，N·m；Fwxi为车轮所受纵向力，N；下标i=(lf，rf，lr，rr)分别为左前车轮、右前车轮、左后车轮和右后车轮；下同。

1.6 车辆所受广义力

车辆所受的广义力可以通过每个车轮在坐标系A下所受的纵向力Fxai、侧向力Fyai以及力矩求和得到。

(6)

式中:Bf，Br分别为前轮距和后轮距，m。

1.7 各轮纵向力和侧向力

各车轮在坐标系A下的纵向力Fxai和侧向力Fyai可通过其在车轮坐标系下纵向力Fxwi、侧向力Fywi及其转角δi得到：

(7)

车轮坐标系下车轮的纵向力和侧向力可以通过轮胎模型求取。轮胎模型是相当复杂的一个问题，目前较为常用非线性轮胎模型有魔术轮胎模型、Dugoff轮胎模型、统一轮胎模型等。多种轮胎模型都可根据车轮的侧偏角αwi、滑移率swi、外倾角γwi、垂直载荷Fzwi及路面摩擦系数μ计算出车轮所受到的纵向力Fxwi和侧向力Fywi。笔者采用魔术轮胎模型，其参数可从车辆仿真软件Carsim中获得，其表达式如式(8)：

(8)

1.8 各轮的纵向和侧向速度

各轮的纵向速度是计算车轮侧偏角和车轮滑移率的重要参数。

(9)

(10)

1.9 各轮侧偏角

根据车轮侧偏角的定义可以表述为：

(11)

1.10 各轮滑移率

为体现车轮在驱动和制动时所产生滑移率不同，可以给定制动时滑移率为负，而驱动时滑移率为正：

(12)

1.11 各轮垂直载荷计算

车轮垂直载荷转移在文献[1-7]都有提及，其表述形式也略有不同，在此给出了一个较为完整的车辆垂直载荷转移公式[5]。它包含了纵向加速度、侧向加速度、悬架作用力对车轮垂直载荷的影响：

(13)

到此，非线性8-DOF模型建立完成，上述13个方程(组)在MALTLAB中编辑成S-Function，以车轮转角、驱动力矩和制动力矩作为输入，以车辆的侧向加速度、横摆角速度等作为输出，可对车辆的操纵稳定性进行研究。

2 车辆模型简化仿真分析

为在仿真工况中尽可能表现车辆特性，在此采用J-turn仿真分析。前轮转角输入如图2，并假设δlf=δrf=δf，δlr=δrr=0，Twdi=Twbi=0，初始车速设为20m/s，将无任何简化的式(1)～式(4)的仿真结果记为Model_0。车辆模型参数[10]如表1。

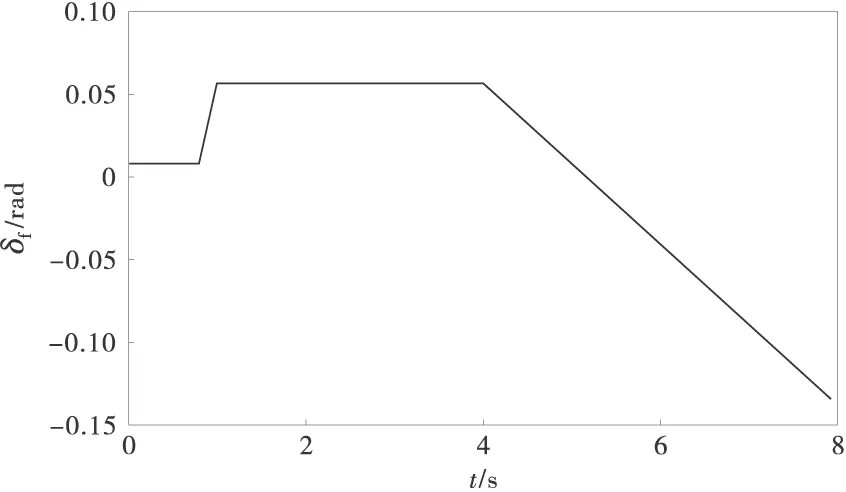
图2 转角输入

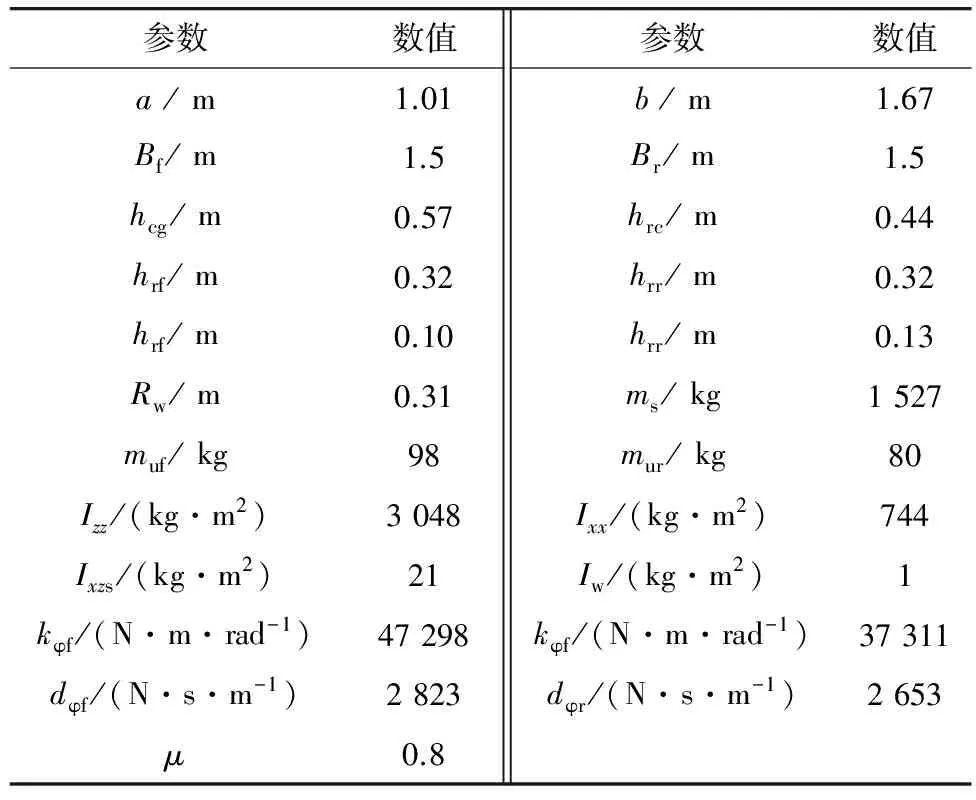
参数数值参数数值a/m1．01b/m1．67Bf/m1．5Br/m1．5hcg/m0．57hrc/m0．44hrf/m0．32hrr/m0．32hrf/m0．10hrr/m0．13Rw/m0．31ms/kg1527muf/kg98mur/kg80Izz/(kg·m2)3048Ixx/(kg·m2)744Ixzs/(kg·m2)21Iw/(kg·m2)1kφf/(N·m·rad-1)47298kφf/(N·m·rad-1)37311dφf/(N·s·m-1)2823dφr/(N·s·m-1)2653μ0．8

2.1 假设侧倾角很小同时忽略簧载质量惯性积

在文献 [1-7]中都有这样的假设条件：侧倾角很小，簧载质量惯性积很小。当侧倾角很小时，则sinφ≈0，cosφ≈1；而簧载质量惯性积很小则Ixz≈0。将两个假设条件代入式(1)～式(4)中，将仿真结果与未有任何简化的model_0进行对比，结果如图3。从图3中可以看出，即使侧向加速度达到0.6g(约6 m/s2)时，两者在侧向加速度、质心侧偏角β=tan(v/u)、横摆角速度及车身侧倾角上都没有明显差异。因此上述假设合理可行，使运动微分方程大大简化。

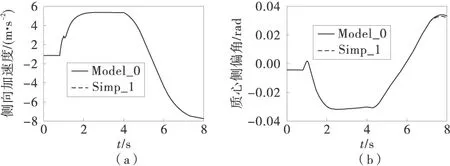
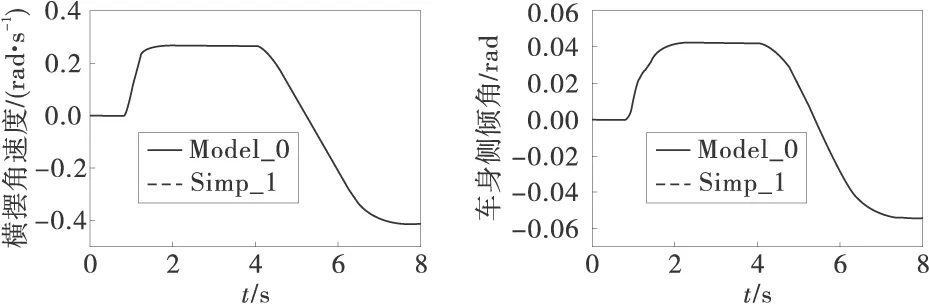
图3 Simp_1对车辆响应的影响

2.2 忽略侧倾角速度及角加速度

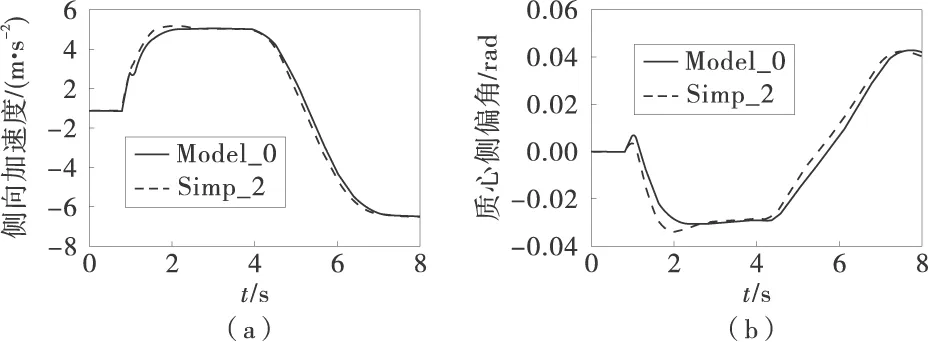
图4 Simp_2对车辆响应的影响

从图4中可以看出，Simp_2轻微的影响了车辆响应的瞬态特性，而在2～4 s之间的稳态转向时车辆响应特性没有改变。

2.3 忽略非簧载质量力矩

在Simp_1成立的基础上，忽略非簧载质量的力矩影响，即假设式(1)～式(3)中amuf-bmur=0。在此条件下仿真结果如图5。

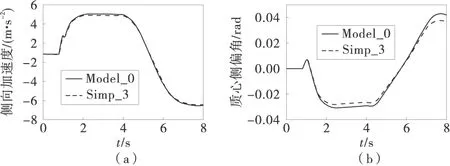
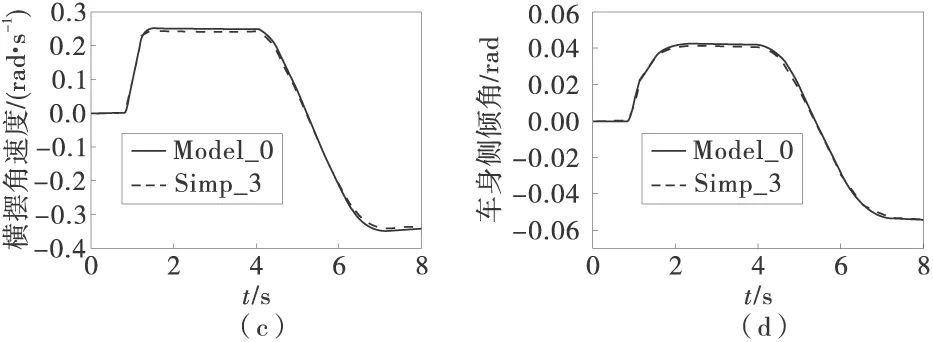
图5 Simp_3对车辆响应的影响

从图5中可以看出，Simp_3轻微改变了车辆的稳态特性，车辆质心侧偏角在2～4 s时的稳态值有所下降，但此简化对瞬态特性没有影响。

2.4 最简形式

当同时考虑Simp_2和Simp_3的情况下，可以得到车辆纵向、侧向、横摆和侧倾运动方程的最简形式，即：

(14)

以最简形式再次进行J-Turn转向仿真，结果如图6。从图6中可以看出，此简化影响了车辆的瞬态特性和稳态特性，但整个影响并不是很大。若对方程(14)再次简化，将引起仿真结果的大幅度失真。所以在模型仿真精度要求不是特别高时，方程(14)是对车辆侧向动力学非线性8DOF运动方程的最简描述。

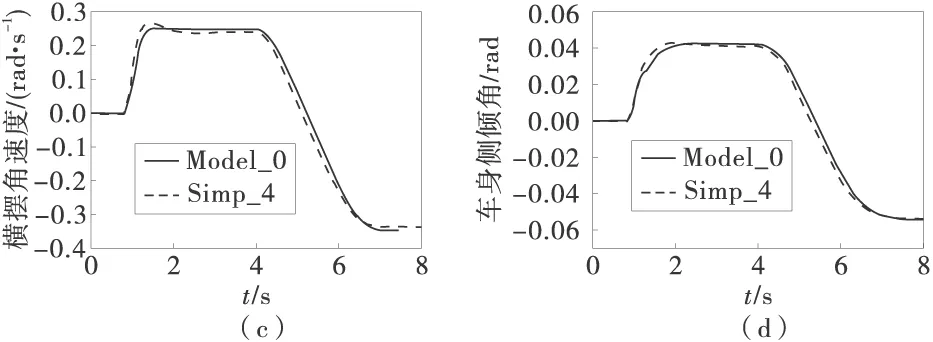
图6 最简形式

3 结 语

给出了车辆侧向动力学的非线性8-DOF模型的完整描述，分析了纵向、侧向、横摆及侧倾运动方程在不同简化情况下对整车仿真精度的影响，最后给出了一种合理的最简形式。最简形式表明：侧倾角很小、忽略簧载质量惯性积、不考虑侧倾角速度及角加速度对纵向、侧向、横摆运动的影响，省略非簧载质量力矩这4种简化形式对非线性8-DOF模型仿真结果影响很小，这些假设合理可行，在不影响仿真精度的同时大大降低了方程的复杂程度。

[1] Wu Jianyoung,Wang Qingping,Wei Xue,et al.Studies on improving vehicle handling lane keeping performance of closed-loop driver-vehicle system with integrated chassis control [J].Mathematics and Computers in Simulation,2010,80(12):2297-2308.

[2] Ding Nenggen,Taheri S.An adaptive integrated algorithm for active front steering and direct yaw moment control based on direct Lyapunov method [J].Vehicle System Dynamics,2010,48(10):1193-1213.

[3] Yang Xiujian,Wang Zengcai,Peng Weili.Coordinated control of AFS and DYC for vehicle handling and stability based on optimal guaranteed cost theory [J].Vehicle System Dynamics,2009,47(1):57-79.

[4] Horiuchi S,Okada K,Nohtomi S.Analysis of accelerating and braking stability using constrained bifurcation and continuation methods [J].Vehicle System Dynamics,2008,46(Sup1):585-597.

[5] Shim T,Ghike C.Understanding the limitations of different vehicle models for roll dynamics studies [J].Vehicle System Dynamics,2007,45(3):191-216.

[6] Boada M J L,Boada B L,Munoz A,et al.Integrated control of front-wheel steering and front braking forces on the basis of fuzzy logic [J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2006,220(3):253-267.

[7] Boada B L,Boada M J L,Diaz V.Fuzzy-logic applied to yaw moment control for vehicle stability [J].Vehicle System Dynamics,2005,43(10):753-770.

[8] 喻凡,林逸.汽车系统动力学[M].北京:机械工业出版社,2005. Yu Fan,Lin Yi.Vehicle System Dynamics [M].Beijing:Mechanical Industry Press,2005.

[9] Pacejka H B.Tire and Vehicle Dynamics [M].Oxford:Butterworth Heinemann,2002.

[10] Demerly J D,Youcef-Toumi K.Non-Linear analysis of vehicle dynamics (NAVDyn):a reduced order model for vehicle handling analysis [J].SAE Technical Paper,2000(1):1621.

Simplification Analysis on the Nonlinear 8-DOF Vehicle Model

Liu Gang1, Wang Changle1, Zheng Kaifeng2, Wang Wenzhu1

(1. School of Mechanical Engineering, Shenyang Aerospace University, Shenyang 110136, Liaoning, China;2. Chinese North Vehicle Research Institute, Beijing 100072, China)

Nonlinear eight degree of freedom (8-DOF) vehicle model has been widely used to study the motion of vehicle and to develop various vehicle control systems. Referring to many literatures, it was found that the longitudinal, lateral, yaw and roll equations of motion in the 8-DOF model had a large difference. Aiming at these simplification forms, a full nonlinear 8-DOF vehicle model was developed and the effect of different simplified terms on the whole vehicle dynamic response characteristics was discussed. At last, a reasonable simplest form was given.

vehicle engineering;nonlinear 8-DOF vehicle model; simplification analysis; simplest form

10.3969/j.issn.1674-0696.2015.04.29

2013-08-20；

2014-05-15

沈阳航空航天大学大学生创新计划项目(dcx2014192)

刘 刚(1975—)，男，辽宁沈阳人，讲师，博士，主要从事悬架理论与控制方面的研究。E-mail:liugang_209209@163.com。

U461.1

A

1674-0696(2015)04-147-04