基于C # 与MATLAB混合编程的物流需求预测系统的实现

许茂增，余国印

(重庆交通大学 管理学院，重庆 400074)



基于C # 与MATLAB混合编程的物流需求预测系统的实现

许茂增，余国印

(重庆交通大学 管理学院，重庆 400074)

根据物流需求数据的不同特点，归纳了灰色GM(1,1)模型、移动平均值模型、指数平滑模型、季节指数模型、BP神经网络模型、线性回归模型、多项式拟合模型和非线性回归模型8种常见的物流需求预测模型，并据此为物流企业开发了基于C # 与MATLAB混合编程的物流需求预测系统，降低了物流企业物流需求预测的复杂度。最后通过预测实例表明该系统具有较好的适用性和较高的预测精度。

管理工程；混合编程；物流需求预测系统

0 引 言

物流需求预测是物流企业进行资源合理配置过程中的重要环节，同时也是制定业务计划和企业发展规划的基础性工作。对物流需求进行准确预测，更有利于企业发展战略等的制定，因此如何寻找最合适的预测方法，获得更高的预测精度，是企业关注的重点问题[1]。

在物流需求预测的理论研究上，学者们根据物流需求数据的不同特征，成功地应用各种预测方法对物流需求进行了预测。如：马凯等[2]结合交通规划四阶段法的特点，在城市物流规划中的物流需求预测基础上,研究了物流需求分阶段的预测方法，并对物流需求预测模型进行了应用分析；周晓娟等[3]根据河北省物流需求呈线性变化的特点，应用多元线性回归对其物流需求进行了预测；闫娟等[4]将区域物流需求与地区经济、产业结构和资源分布密切联系起来，并针对其较强的非线性变化和历史数据小的特征，提出了一种新的基于泊松分布的神经网络需求预测算法；而在物流需求历史数据充足的情况下，后锐等[5]应用MLP神经网络预测法提高了物流需求预测的精度；杨蕾等[6]则采用随机时间序列模型对与时间序列强烈相关的物流需求进行预测；司玲玲等[7]指出，物流受多种因素的影响，其需求具有趋势性、较大波动性和随机性等变化特点，据此首先利用灰色GM(1,1)预测模型动态预测物流需求变化趋势，然后利用支持向量机(SVM)对预测结果进行修正，取得了较好的预测效果；施泽军等[8]提出了在灰色模型GM(1，1)和三次指数平滑法基础上的组合预测方法，并将其应用到港口物流中的集装箱吞吐量预测中；刘智琦等[9]在考虑不同因子对物流需求影响的基础上，建立了因子分析和神经网络相结合的物流需求预测模型；此外，根据物流需求数据的实际特点，李自立等[10]运用主成分分析法预测了湖北省区域物流需求；欧阳小迅等[11]建立了一个非线性的物流需求计量模型；耿立艳等[12]提出一种基于灰色关联分析的最小二乘支持向量机物流需求预测方法，均取得了较好的预测效果。

实践中，由于这些研究所使用的预测方法均以专业的理论为支撑，如BP神经网络预测法包含了神经网络理论和编程技术，不易为一般物流企业管理人员掌握使用，从而导致这些预测技术在物流企业中没有得到广泛的应用。此外，在预测系统的开发方面，目前尚未有专门集成物流需求预测方法的预测系统。而市场上主要的预测软件SPSS、Eviews等集成的方法并非专门针对物流需求数据的特征而设计，预测效果不理想。因此，针对物流需求数据的不同特征，综合研究各种物流需求预测方法，开发一套集成物流需求预测常用方法的预测系统对于物流企业的物流需求预测工作十分必要。

在开发工具上，MATLAB的计算功能很强大，但其界面开发能力较差。C # 在设计开发Windows应用程序方面界面友好，方便快捷[13]。因此笔者基于MATLAB和C # .NET，充分利用两者各自的优点，开发出了适合物流企业进行物流预测的专门系统，提高了物流企业物流预测的准确性。同时，该系统对使用者的理论要求不高，便于物流企业管理人员掌握。

1 C #.NET与MATLAB接口

通过C #.NET与MATLAB接口技术进行混合开发，该系统集成了C # 和MATLAB各自的优点，把计算过程和数据图形显示功能留给MATLAB完成，而用C # 语言编写Windows应用程序，对计算结果进行分析和可视化处理，极大地提高了程序的开发效率[14]。表1为C #.NET与MATLAB接口的主要方法。

表1 C#.NET与MATLAB的主要接口方法

(续表1)

序号方法介绍④MATLAB引擎技术应用程序运行时一般是先向MATLAB计算引擎组件传送数据和命令，再由MAT⁃LAB计算引擎与MATLAB服务器交互，最后由MATLAB计算引擎将运算结果返回给应用程序。

表1中的4种方法中，第1种方法调用过程复杂，且实现的功能有限；第2种方法计算速度慢；第3种方法的优点在于利用C # 访问该组件时，没有必要进行环境切换，因此可以获得最快的运行速度。此外，通过实验证明，在 .NET调用MATLAB神经网络工具箱时，前3种方法都是不可行的，只有MATLAB引擎技术能够支持该调用。因此，本系统最终采用了第3、第4这两种方法进行对MATLAB的调用。

1)首先，对利用.NET组件技术调用MATLAB的流程进行简要介绍。

步骤1：新建工程。选择New Deployment Project→MATLAB Builder NE→.NetComponent，输入工程名称“yuce”并选择保存位置。

步骤2：添加M文件。选择projectAdd file，把需要编译的M文件全部添加到相应的文件夹中。

步骤3：编译、打包。选择 tools→Build编译成.NET组件，点击 tools→Package进行打包。

步骤4：新建C # 项目，添加引用。

2)C # .NET环境下利用MATLAB引擎技术实现神经网络(图1)的步骤如下。

步骤1：编制M文件。在BP.m文件中编制了神经网络的实现逻辑，其函数定义为：

Function[wucha,yuce]=BP(input,cs1,cs2,hanshu1,hanshu2,hanshu3,hanshu4)

其中：input表示输入的历年物流需求量数据；cs1，cs2表示网络的训练参数，hanshu1，hanshu2，hanshu3，hanshu4表示网络的传递函数和网络训练函数；wucha表示输出预测的标准误差；yuce表示最终的预测值。

步骤2：在Visual Studio.NET中添加COM引用“MATLAB Application(Version 7.13) Type Libray”，实例化引擎对象。

MLApp.MLApp MATLAB= new MLApp.MLApp ()。

步骤3：使用引擎对象提供的PutFullMatrix，GetFullMatrix，Execute这三个接口进行对MATLAB神经网络工具箱的调用，参考代码为：

MATLAB.PutFullMatrix("input", "base", x, x1);//向MATLAB Server中添加数据；

MATLAB.Execute(@"[wucha,yuce]=BP(input,cs1,cs2,hanshu1,hanshu2,hanshu3,hanshu4)");

MATLAB.GetFullMatrix("yuce", "base", ref yc, ref yuce_pi); //向MATLAB Server中读取数据，yc和yuce_pi为预先定义好的System. Array对象；

yc.CopyTo(yucezhi, 0);//将预测结果保存到yucezhi数组中。

图1 C # .NET调用MATLAB工具箱过程

2 预测方法

集成到该系统中的数据处理方法有：移动平均值预测法、灰色GM(1,1)预测法、指数平滑预测法、季节指数预测法、BP神经网络预测法[15]、线性回归预测法、多项式拟合法和非线性回归预测法，如表2。其中，移动平均值预测法集成了1次和2次平均值移动法，指数平滑法包括1次、2次、3次指数平滑法，季节指数有水平模型、趋势模型和环比法模型，线性回归中有一元和多元线性回归预测法，而非线性回归预测法集成了双曲线、幂函数、倒幂函数、对数曲线、S曲线、指数曲线、倒指数曲线、皮尔生长曲线等模型。这些方法都是常用的物流需求预测方法，在使用该系统时可以根据数据的特征，选择一种或多种方法进行预测。

表2 系统集成预测方法

(续表2)

预测方法方法核心思想适用条件线性回归根据样本观测值对线性模型的参数进行估计，求得回归方程，然后对回归方程、回归系数进行显著性检验，最后利用回归方程进行预测自变量与因变量为线性关系多项式拟合以多项式曲线拟合数据，使数据点的误差平方和最小因变量为自变量的多项式非线性回归与线性回归预测相比，针对非线性模型进行预测自变量与因变量为非线性关系

3 系统设计与实现

本系统是基于Visual Studio 2010和MATLAB 2011平台开发的，Visual Studio用于系统用户界面的设计与开发，MATLAB负责科学计算和图形的绘制功能。系统采用了C/S架构。

如图2，系统主要分为基础数据、预测方法、预测效果检验、帮助等模块。其中，基础数据模块负责数据输入等数据处理工作；预测方法模块则提供了以上介绍的8种预测方法，用户可以根据实际情况选择其中一种或者多种方法进行预测；在预测效果检验模块中用户可以通过预测的标准误差值来比较不同预测方法的预测效果，也可从图形中直观地进行判断，从而选择最优的预测结果。帮助模块对系统中集成的预测方法以及系统的使用方法进行了详细说明。

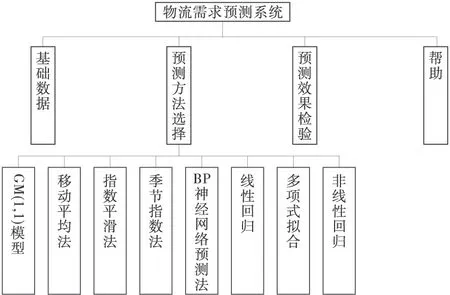
图2 系统功能结构

4 预测实例

为测试系统对于物流需求预测的适用性及预测精度，笔者收集了1993—2012年相应的数据(表3)，并选取GM(1,1)模型、移动平均法、指数平滑法、BP神经网络预测法、线性回归、多项式拟合和非线性回归法对2013年的物流需求量进行了预测。其中，对于社会物流需求的衡量，参照《中国物流年鉴》[16]统计数据说明，用“社会物流总额”(由工业品、农产品、进口货物、再生资源、单位与居民物品组成)来表示。该指标从其结构成分来看，既包含了产业结构因素，也包含了流通消费领域，研究的层面较为全面。而对于线性回归预测法，采用GDP、物流总费用、全社会固定资产投资、进口总额和出口总额等指标作为模型变量。

表3 物流需求及经济指标统计数据

表3资料社会物流总额和物流总费用来源于《中国物流统计年鉴》[16]。

图3、图4为线性回归预测法的界面和预测效果。通过线性回归预测，社会物流总额与固定资产投资总额和进口总额相关，表达式为：

社会物流总额=3.677 7×全社会固定资产投资+3.916 1×进口总额

图3 线性回归预测界面

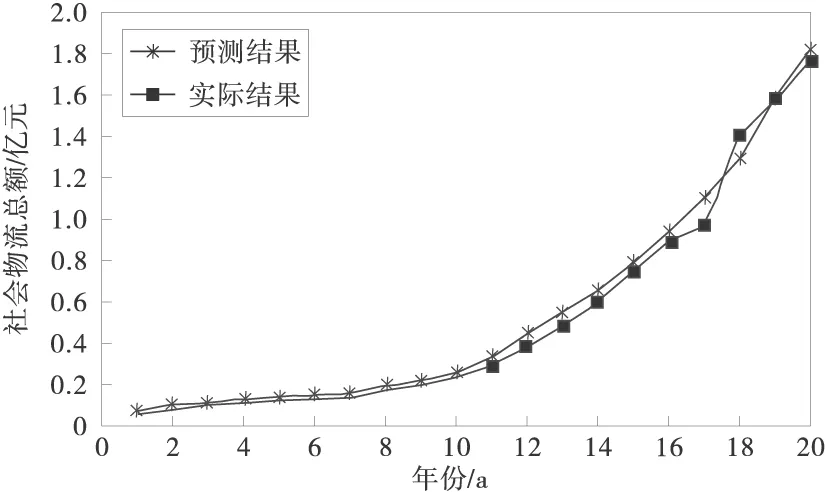
图4 线性回归预测效果

图5为各种预测方法的预测效果。从图5中可以看出各种预测方法的预测标准误差从小到大分别为：多元线性回归、非线性预测法(幂函数)、多项式拟合(2次)、灰色预测法、指数平滑法(3次)、简单移动平均法和BP神经网络预测法。故应该以多项式拟合预测法的预测值作为最终的预测值。通过该系统，2013年社会物流需求量最终的预测值为2 079 644亿元，而国家统计局、国家发改委、中国物流与采购联合会联合发布的数据为1 978 000亿元，预测相对误差为-5.1%，说明该系统对于物流需求预测具有良好的适用性且预测精度较高。

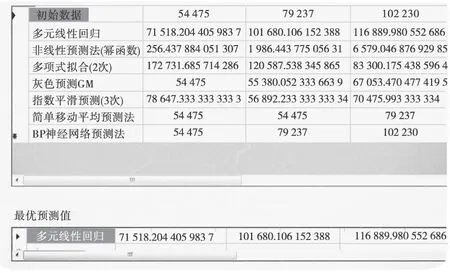
图5 各种预测方法预测效果检验

5 结 语

笔者在研究各种物流需求预测方法的基础上，充分利用MATLAB强大的科学计算能力和C # .NET方便快捷的界面设计功能，通过混合编程技术将两者集成在一起，以此为物流企业开发了集成物流需求预测常用方法的物流需求预测系统。通过预测实例表明，该系统对于物流需求预测具有很好的适用性，预测精度较高。系统操作简单，对使用者的专业知识要求不高，容易被物流企业管理人员掌握和使用。鉴于该系统操作的简便性和预测的准确性，系统的使用将会提高物流企业对于物流需求预测的可操作性以及预测精度，对物流企业具有重要的实际意义。

[1] Rodrigo A G,Hani S M.Forecasting freight transportation demand with the space-time multinomial probity model [J].Transportation Research:Part B,2000(34):403-418.

[2] 马凯，艾力·斯木吐拉.交通规划四阶段法在物流需求预测中的应用[J].重庆交通大学学报：自然科学版,2009,28(4):745-750. Ma Kai,Eili Ismutull.Application of four-step method of traffic planning to logistics demand forecast [J].Journal of Chongqing Jiaotong University:Natural Science,2009,28(4):745-750.

[3] 周晓娟,景志英.基于多元线性回归模型的河北省物流需求预测实证分析[J].物流技术,2013,32(5):270-272. Zhou Xiaojuan,Jing Zhiying.Empirical analysis of logistics demand forecasting of Hebei based on multi-linear regression model [J].Logistics Technology,2013,32(5):270-272.

[4] 闫娟,李萍.泊松分布灰色理论在物流需求预测中的应用[J].计算机仿真,2012,29(4):229-233. Yan Juan,Li Ping.Application research of poisson distribution grey theory in logistics demand forecasting [J].Computer Simulation,2012,29(4):229-233.

[5] 后锐,张毕西.基于MLP神经网络的区域物流需求预测方法及其应用[J].系统工程理论与实践,2005(12):43-47. Hou Rui,Zhang Bixi.A method for forecasting regional logistics demand based on MLP neural network and its application [J].Systems Engineering-theory & Practice,2005(12):43-47.

[6] 杨蕾,张苗苗.时间序列模型在物流需求预测中的应用[J].商业时代,2013(13):26-27. Yang Lei,Zhang Miaomiao.The application of time series model in logistics demand forecasting [J].Commercial Times,2013(13):26-27.

[7] 司玲玲,王亚楠,徐贵军.改进灰色模型在物流需求预测中的应用[J].计算机仿真,2012,29(6):192-194. Si Lingling,Wang Ya’nan,Xu Guijun.Logistics demand forecasting based on improved grey model [J].Computer Simulation,2012,29(6):192-194.

[8] 施泽军,李凯.基于灰色模型和指数平滑法的集装箱吞吐量预测[J].重庆交通大学学报：自然科学版,2008,27(2):302-204. Shi Zejun,Li Kai.Container throughput forecasting based on gray method and exponential smoothing method [J].Journal of Chongqing Jiaotong University:Natural Science,2008,27(2):302-204.

[9] 刘智琦,李春贵,陈波.基于因子分析与神经网络的区域物流需求预测[J].计算机仿真,2012,29(6):359-362. Liu Zhiqi,Li Chungui,Chen Bo.Regional logistics demand forecast based on factor analysis and neural network [J].Computer Simulation,2012,29(6):359-362.

[10] 李自立,黄芬.基于主成分分析的区域物流需求预测指标研究[J].物流技术，2009,28(12):128-130. Li Zili,Huang Fen.Research on the forecasting indices of regional logistics demand based on PCA [J].Logistics Technology,2009,28(12):128-130.

[11] 欧阳小迅,戴育琴.社会物流需求的非线性模型分析[J].商业时代,2009(20):23-24. Ouyang Xiaoxun,Dai Yuqing.Non-linear model analysis of social logistics needs [J].Commercial Times,2009(20):23-24.

[12] 耿立艳,丁璐璐.基于灰关联分析的最小二乘支持向量机物流需求预测[J].物流技术,2013,32(10):130-132. Geng Liyan,Ding Lulu.Forecasting of logistics demand based on grey correlation analysis and least square SVM [J].Logistics Technology,2013,32(10):130-132.

[13] 黄海宽,张云锋,魏东,等.基于COM的MATLAB在中药分析中的应用[J].自动化与仪表,2006(4):5-7. Huang Haikuan,Zhang Yunfeng,Wei Dong,et al.Application of MATLAB based on COM in Chinese medicine [J].Automation & Instrumentation,2006(4):5-7.

[14] 黄一丹,严洪森,冯丽娟,等.基于C#.NET与Matlab接口和BP网络的汽车产量预测[J].计算机技术与发展,2008,18(11):36-40. Huang Yidan,Yan Hongsen,Feng Lijuan,et al.Vehicle production forecasting based on BPNN and interface between C#.NET and Matlab [J].Computer Technology and Development,2008,18(11):36-40.

[15] 谭伟,陆百川,黄美灵.神经网络结合遗传算法用于航迹预测[J].重庆交通大学学报：自然科学版,2010,29(1):147-150. Tan Wei,Lu Baichuan,Huang Meiling.Track prediction based on neural networks and genetic algorithm [J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(1):147-150.

[16] 中国物流与采购联合会.中国物流年鉴[M].北京:中国财富出版社,2013. China Federation of Logistics & Purchasing.China Logistics Yearbook [M].Beijing:China Fortune Press,2013.

Implementation of Logistics Demand Forecasting System Based onHybrid Programming with C # and MATLAB

Xu Maozeng, Yu Guoyin

(School of Management, Chongqing Jiaotong University, Chongqing 400074, China)

According to different characteristics of logistics demand data ,8 common logistics demand forecasting models was summarized, such as, the grey GM (1,1) model, the moving average model, the exponential smoothing model, the seasonal index model，BP neural network model, linear regression model, polynomial fitting model and nonlinear regression model and so on. On the basis of it, a logistics demand forecasting system based on the hybrid programming technology with C # and Matlab was developed for the logistics enterprises, and it reduced the complexity of logistics demand forecasting in the logistics enterprises. Finally, the forecasting example shows that the system has good applicability and high forecasting accuracy.

management engineering; hybrid programming; logistics demand forecasting system

10.3969/j.issn.1674-0696.2015.04.25

2013-06-11；

2014-06-22

教育部人文社科研究项目(10XJA790009)

许茂增(1960—)，男，陕西大荔人，教授，博士生导师，主要从事物流与供应链管理方面的研究。E-mail：xmzzrxhy@eyou.com。

F252.21；TP311

A

1674-0696(2015)04-128-05