粗糙单裂隙溶质运移优先通道的模拟研究

余 成，雷文武

(重庆交通大学 河海学院，重庆 400074)



粗糙单裂隙溶质运移优先通道的模拟研究

余 成，雷文武

(重庆交通大学 河海学院，重庆 400074)

为考察岩石粗糙裂隙内不均匀分布的裂隙空间对溶质运移过程的影响，采用基于LCL方法的数值模型对不同裂隙宽度下的流场和溶质运移过程进行模拟。结果表明：随着裂隙宽度减小，流场逐渐从均匀的平行板流过渡到强烈不均匀的沟槽流，流线逐渐集中于部分优先沟槽通道；溶质运移锋面的推进也从基本呈直线状平行推进，逐渐开始不规则化，出现指流现象；随着宽度继续减小，沟槽通道进一步发展，形成贯穿整个流场的溶质运移优先通道；优先运移通道的溶质运移速度远大于其他部位，出现某些部位溶质运移受困而滞留的现象。因此，在裂隙宽度较小时，粗糙裂隙内的优先沟槽通道对裂隙流动和溶质运移过程有着非常重要的影响。

水利工程；粗糙裂隙；溶质运移；数值模拟；优先沟槽通道

0 引 言

粗糙裂隙内流体流动与溶质运移过程在岩土工程、油气工程及环境工程领域受到极大的重视。裂隙流及溶质运移过程可能直接影响地下污染物的释放和运移过程[1]。在核废料地下填埋的处理工作中，地下岩体裂隙的水力渗透特征及其对溶质运移过程的影响也受到关注[2]。裂隙在地下岩体中常常以裂隙网络的形式存在，但截至目前，人们对流体和溶质在单条粗糙裂隙内运动过程的了解还不够深入，对于单裂隙内水流和溶质运移过程的研究仍然是水文学和环境科学的一大热点[3-5]。

其中的难点主要在于裂隙空间和流场分布的不规则性。裂隙表面具有典型的分形特征[6]，其随机性决定了裂隙表面的粗糙性和复杂性。在裂隙宽度较大时，表面粗糙性对流动和溶质运移过程的影响较小，但裂隙宽度减小时，表面粗糙性对流场的影响则显著增大[7]。另外由于岩石碎裂时常常伴随着相互错动，使得裂隙内部空间分布强烈不均。随着裂隙宽度减小，各处宽度的相对差异逐渐增大。宽度较小的部位水力渗透性较差，不利于流体流动，而宽度较大的部位则可能形成局部优先沟槽通道[8]。优先沟槽通道一方面使裂隙呈现局部透水特征，另一方面也影响着流动及溶质运移过程的规则性。裂隙面的复杂性决定了沟槽通道的复杂性，以及流动和溶质运移过程的复杂性。至今人们对于粗糙裂隙内流动和溶质运移过程依然缺乏更加深入的研究。

笔者运用LCL模型对粗糙裂隙内的流动和溶质运移过程进行模拟研究。流动模型显示，随着裂隙宽度减小，流场逐渐从均匀的平行板流过渡到强烈不均匀的沟槽流，流线逐渐集中于部分优先沟槽通道；溶质运移过程受到沟槽通道较强的影响；裂隙宽度较大时，浓度运移锋面基本呈直线状平行推进，宽度减小时，浓度推进锋面逐渐不规则化，出现指流现象，宽度继续减小，沟槽通道进一步发展，指流现象也进一步演化，形成贯穿整个流场的溶质运移优先通道；优先运移通道的溶质运移速度远大于部分局部的溶质运移速度，出现某些局部溶质运移受困而迟滞的现象。

1 粗糙裂隙面的随机生成

裂隙表面是具有分形特征的粗糙表面。实践中用于生成分形地形表面的建模方法有分数维布朗运动法、傅立叶滤波法、小波变换法、中点随机位移法等。笔者采用比较流行的菱形-方形细分法(Diamond-Square)。其原理可以简述为：首先对于给定的正方形区域，假设4个角点A,B,C,D赋值高程分别为hA，hB，hC，hD，随后的过程分为Diamond步和 Square步。

1.1 Diamond步

给正方形的中心点赋高程值为，如式(1)：

(1)

式中：δ0为扰动随机变量，通常可简单地采用均匀分布U(ξ,-ξ)(表示在该方形区域内高程扰动的上限值)。

1.2Square步

(2)

式中：δ0同前。

如此方形ABCD可被分割为4个小方形，对每一个小方形可使用以上两步进行递归，但在第i层递归中，扰动变量应修改为，如式(3)：

(3)

式中：k为分形表面粗糙度，k∈[0，1]，越小分形表面越粗糙。

2 裂隙流动模型

粗糙裂隙内的流动可以使用复杂边界下的Navier-Stokes方程描述，但直接Navier-Stokes流动模拟具有对网格划分精度要求高、非线性微分方程求解困难等缺点。实践中人们更多地使用局部立方定律(LCL)。LCL认为裂隙的上下表面在局部范围内为平行板，并具有局部渗透系数K：

(4)

式中：b为局部裂隙宽度；v为流体运动黏度系数。

LCL可将定常三维裂隙流简化为二维平面渗流模型，在低雷诺数和通常几何条件下，LCL方法与直接Navier-Stokes模拟之间的差异一般在5%～10%范围内[9]，因此被人广泛接受。

利用随机生成的粗糙表面作为裂隙空间的上下表面，通过上下表面间的水平和垂向相对运动可生成不均匀分布的裂隙空间，如图1。裂隙空间的分布与表面粗糙性有关外，还与裂隙表面间的相对位置有关。相对的水平、垂向以及倾斜、旋转等都可能使裂隙空间发生不规则变化。笔者主要考察上下表面在固定水平相对位移(x，y方向)时，垂直(z方向)位移变化过程中的裂隙空间变化，以及相应地流动和溶质运移过程所受到的影响。

模型采用了的有限差分网格，每个网格宽度为0.1mm(图1)。模型 y 方向的两侧边界被设定为定水头边界，水头差为常数0.1mm；模型x方向的两侧边界被设定为隔水边界。

图1 文中模型所采用的粗糙裂隙宽度的空间分布

3 溶质运移模型

溶质运移模型依赖于流动模型，但溶质运移除了有对流运动外，还有明显的扩散和弥散运动。由于速度边界层的影响，裂隙流体速度在宽度方向上呈不均匀分布，导致较为显著的弥散效应。对于平行板流动，溶质弥散系数D由流体性质和平行板间距决定，如式(5)[10-11]：

(5)

式中：D*为分子扩散系数；b为裂隙宽度；U为裂隙流的平均流速。

对于裂隙流，理论上D在空间上呈不均匀分布，但由于较难统计裂隙各处流量，且在b较小时弥散作用对溶质运移过程的影响比对流速度较小，因此笔者近似地认为D在空间上为均匀分布，其大小利用裂隙流平均流速和裂隙平均宽度计算。

为了考察定常流场状态下溶质的运移过程，模型中溶质被认为从0时刻开始以定浓度的方式释放在模型的定水头边界。通过考察溶质分布状态以及溶质运移前锋面的推进过程，研究优先沟槽通道对溶质运移过程的影响。裂隙流动模型采用MODFLOW程序实现，溶质运移模型采用MT3DMS程序实现。

4 结果与讨论

4.1 导水系数变化

则本例中，当α=-0.119时，依然可以很好地满足立方定律(图2)，说明在h=0时，由于水平错动形成的沟槽通道的影响，可以认为是一个宽度为0.119mm的附加裂隙宽度。

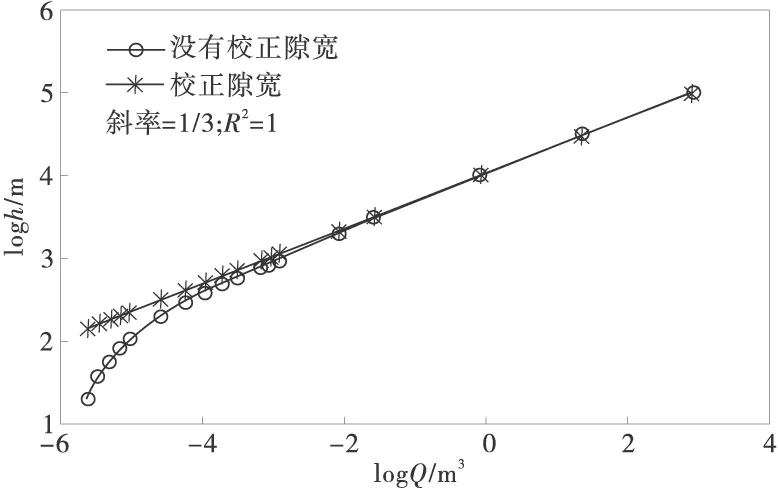
图2 粗糙裂隙导水系数与测量平均隙宽和校正平均隙宽之间的关系

4.2 裂隙流场变化

裂隙上下表面垂向运动时，各处间的渗透系数值变化差异巨大。通常较宽部位的值变化程度较小，而较窄部位的值受影响较大。相应地，裂隙流场形态、等水头线及流线分布也必然受到影响。如图3，裂隙宽度较大时，流场状态比较接近于平行板流，流线与等水头线主要呈平行直线分布；但在宽度减小时，渗透系数的不均匀性最终使得流线和水头分布也越加曲折。

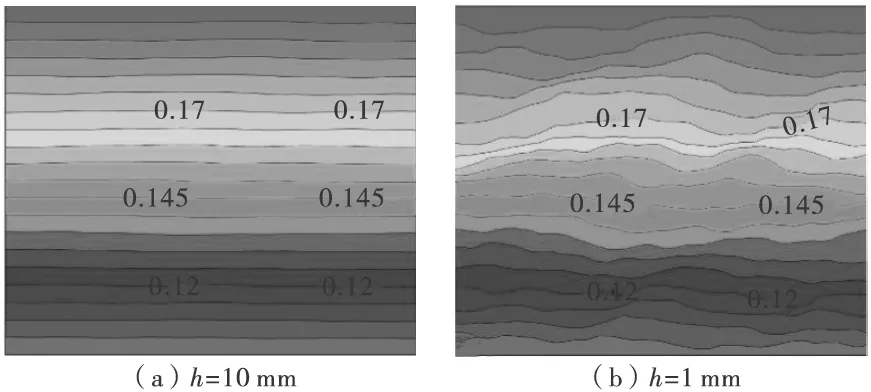
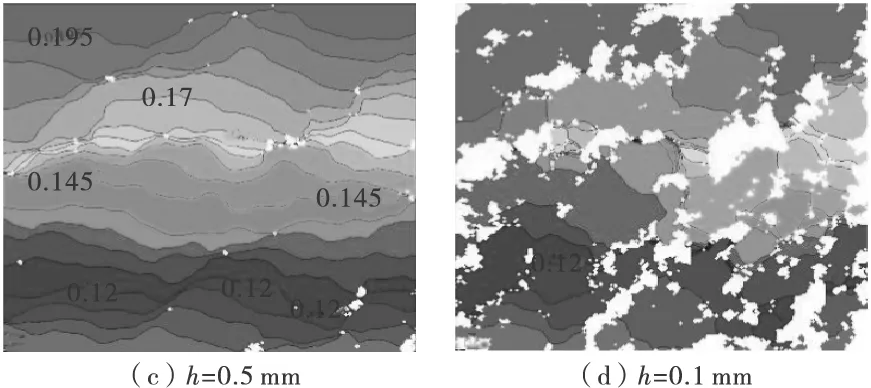
图3 不同裂隙宽度下的等水头线

随着裂隙各处值相对差异变大，水头梯度逐渐集中于裂隙通道比较狭窄的部位。表明随着沟槽通道的逐渐形成，这些沟槽通道尤其是其中比较狭窄的部位，将逐渐成为裂隙水力渗透性的重要影响因素。对应地，流线分布特征(图4)也反映出在优先沟槽通道逐渐形成的过程中流动逐渐向沟槽通道不断集中的过程。

图4 不同裂隙宽度下的流线分布

4.3 溶质运移锋面变化

流动过程的变化必然引起溶质运移过程的变化。优先沟槽通道也很大程度地影响了裂隙流的溶质运移过程。裂隙宽度变化以及沟槽通道形成的过程中，裂隙流动速度的变化不仅整体上影响了溶质运移的速度，同时，裂隙流不断集中的过程也很大程度上影响了浓度的分布状态。

图5显示了不同裂隙宽度下，在特征时刻的典型浓度分布状态。从浓度锋面分布看，在裂隙宽度很大时，裂隙粗糙性的影响很小，浓度锋面形状主要呈平行推进，与平行板间的溶质运移过程极为类似。

图5 不同裂隙宽度下特征时刻的溶质浓度分布

随着裂隙宽度减小，流动逐渐向优先沟槽通道集中，此时浓度运移锋面逐渐出现不均匀变化，锋面上开始出现局部的指流现象，但浓度的整体推进过程依然保持相对一致。此时优先沟槽通道尚处于形成阶段，对溶质运移过程只具有部分的影响，还没有起到决定性作用。

随着裂隙宽度继续减小，流线进一步向沟槽通道集中，溶质运移过程也进一步发生较大变化。浓度锋面的不均匀程度进一步加剧，指流现象进一步演化，发展出非常明显的优先运移通道。由于流场的不均匀性，各处间的溶质运移速度差异明显。此时优先沟槽通道对溶质运移过程逐渐产生决定性的影响作用，浓度锋面推进一致性差，溶质主要沿着优先沟槽通道运移。

在宽度减小过程中，部分局部渗透系数减小迅速，其溶质运移速度远小于优先沟槽通道的溶质运移速度，因此呈现出在某些部位溶质可能陷入局部的“困境”，在裂隙内运移相当缓慢从而长期滞留，从而使裂隙出口处的浓度穿透曲线呈现非常显著的拖尾现象。这与多孔介质中由于机械弥散或者吸附过程的影响而造成的浓度曲线拖尾现象类似。在研究上可以与多孔介质中的溶质运移过程进行类比。

5 结 语

笔者利用LCL方法对粗糙裂隙间的裂隙流动以及溶质运移过程进行了模拟研究。裂隙上下表面通过截取菱形-方形细分法所获得的粗糙表面生成，利用上下表面间的相对运动生成不规则分布的裂隙空间。裂隙流动模型显示，在裂隙宽度逐渐减小过程中，裂隙流逐渐从平行板流过渡到具有强烈不均匀特征的沟槽流，其中逐渐形成的优先沟槽通道对裂隙流场有着较大的影响，流线和水头梯度都逐渐集中于这些优先沟槽通道。

溶质运移过程也较大程度地受到优先沟槽通道的影响。在裂隙宽度较大时，浓度运移的前锋面基本呈直线状的平行推进，在宽度减小时，受到优先沟槽通道的影响，浓度锋面逐渐不规则化，出现局部指流现象。在裂隙宽度继续减小时，优先沟槽通道继续进一步发展，成为影响溶质运移过程的主要因素。指流也进一步发展和演化，形成贯穿整个流场的溶质运移优先通道。优先运移通道的溶质运移速度远大于某些局部的溶质运移速度，因此可能出现某些局部溶质被困而滞留的现象。

[1] 钱家忠,汪家权,葛晓光,等.我国北方型裂隙岩溶水流及污染物运移数值模拟研究进展[J].水科学进展,2003,14(4):509-512. Qian Jiazhong,Wang Jiaquan,Ge Xiaoguang,et al.Advances in research for numerical simulation of contaminant transport and flow in North China type fracture-karst media [J].Advances in Water Science,2003,14(4):509-512.

[2] Seetharam S C,Perko J,Jacques D,et al.Influence of fracture networks on radionuclide transport from solidified waste forms [J/OL].Nuclear Engineering and Design,2014,270:162-175 [2014-02-18].http://www.sciencedirect.com/science/article/pii/S002954931400020X.

[3] Wu Yushu,Ye Ming,Sudicky E A.Fracture-flow-enhanced matrix diffusion in solute transport through fractured porous media [J/OL].Transport in Porous Media,2010,81(1):21-34 [2014-02-11].http://link.springer.com/article/10.1007%2Fs11242-009-9383-4.

[4] Qian J Z,Chen Z,Zhan H B,et al.Solute transport in a filled single fracture under non-Darcian flow [J/OL].International Journal ofRock Mechanics and Mining Sciences,2011,48(1):132-140[2014-02-21].http://www.sciencedirect.com/science/article/pii/S1365160910001796.

[5] 鞠杨,张钦刚,杨永明,等.岩体粗糙单裂隙流体渗流机制的实验研究[J].中国科学:技术科学,2013,43(10):1144-1154. Ju Yang,Zhang Qingang,Yang Yongming,et al.An experimental investigation on the mechanism of fluid flow through single rough fracture of rock [J].Scientia Sinica Technologica,2013,43(10):1144-1154.

[6] Borodich F M.Fractals and fractal scaling in fracture mechanics [J/OL].International Journal of Fracture,1999,95(1/2/3/4):239-259 [2014-02- 15].http://link.springer.com/article/10.1023%2FA%3A1018660604078.

[7] Witherspoon P A,Wang J S Y,Iwai K,et al.Validity of cubic law for fluid flow in a deformable rock fracture [J/OL].Water Resources Research,1980,16(6):1016-1024 [2014-02-23].http://onlinelibrary.wiley.com/doi/10.1029/WR016i006p01016/abstract.

[8] Xiong Xiangbin,Li Bo,Jiang Yujing,et al.Experimental and numerical study of the geometrical and hydraulic characteristics of a single rock fracture during shear [J/OL].International Journal of Rock Mechanics and Mining Sciences,2011,48(8):1292-1302 [2014-02-25].http://www.sciencedirect.com/science/article/pii/S136516091100147X.

[9] Brush D J,Thomson N R.Fluid flow in synthetic rough-walled fractures:Navier-Stokes,Stokes,and local cubic law simulations [J/OL].Water Resources Research,2003,39(4):1085-1100 [2014-02-01].http:// onlinelibrary.wiley.com/doi/10.1029/2002WR001346/abstract.

[10] Aris R.On the dispersion of a solute in a fluid flowing through a tube [J/OL].Proceedings of the Royal Society:A,1956,235:67-77 [2014-02-18].http://rspa.royalsocietypublishing.org/content/235/1200/ 67.

[11] Taylor G.Dispersion of soluble matter in solvent flowing slowly through a tube [J/OL].Proceedings of the Royal Society:A,1953,219:186-203 [2014-02-10].http://rspa.royalsocietypublishing.org/content/ 219/1137/186.

Numerical Modeling of Preferential Flow and Transport Channel between Rough-Walled Fractures

Yu Cheng, Lei Wenwu

(School of River & Ocean Engineering, Chongqing Jiaotong University, Chongqing 400074, China)

In order to show the impact of non-uniform void space on the flow and transport processes between rough-walled fractures, LCL modeling was employed to simulate the process of the solute transport under the flow with different crack width. The result suggests that, along with the decrease of fracture apertures, the flow field tends to get irregular, and streamlines tend to concentrate at preferential flow channels. Solute concentration front looks parallel when the fracture aperture is still significant, but gets irregular and looks similar to finger flow while fracture aperture decreases. As apertures decrease, preferential channels tend to form preferential transport channels. Solute transport speed at preferential transport channels tends to be much higher, thus some of the solute at low permeable regions seems to be trapped, or retarded within fractures. Therefore it can be concluded that when fracture apertures are small, preferential channels have significant impact on flow and transport processes between rough fractures.

hydraulic engineering; rough-walled fractures; solute transport; numerical modeling; preferential flow channel

10.3969/j.issn.1674-0696.2015.04.17

2015-01-12；

2015-04-01

国家自然科学基金项目(51409028)；重庆交通大学科研启动基金项目(2010310002)

余 成(1984—)，重庆人，讲师，博士，主要从事地下渗流及溶质运移方面的研究。E-mail：beimingyu@pku.edu.cn。

P 641.2

A

1674-0696(2015)04-091-04