桩底约束条件对弧形排桩-连系梁内力影响研究
2015-06-07张志伟邓荣贵王振永钟志彬
张志伟,邓荣贵,王振永,钟志彬
(西南交通大学 土木工程学院,四川 成都 610031)
桩底约束条件对弧形排桩-连系梁内力影响研究
张志伟,邓荣贵,王振永,钟志彬
(西南交通大学 土木工程学院,四川 成都 610031)
弧形排桩-连系梁抗滑结构为多次超静定结构,将桩顶弧形连系梁计算模型简化为无铰拱,视抗滑桩与弧形连系梁之间的约束力为冗力,利用桩顶与弧形连系梁之间的变形协调条件,建立了抗滑结构的整体柔度方程;在桩底自由、铰支及固定等3种不同桩底约束条件下,分别求解桩梁之间的约束冗力,比较了3种桩底约束条件下弧形连系梁的内力,及抗滑桩的内力和位移。研究表明:桩底固定时,桩底部弯矩较大;桩底自由时,弯矩明显减小,桩身位移增加;在桩顶连系梁的约束下,减小桩身锚固段长度,能够减小桩身底部弯矩的影响规律。
岩土工程;抗滑结构;弧形排桩;弧形连系梁;桩底约束;内力分布
0 引 言
滑坡是典型的地质灾害之一,可造成巨大的生命财产和经济损失,抗滑桩作为边坡治理的一种有效措施已被广泛应用[1-3]。在抗滑桩加固机理及计算理论研究方面,S.Hassiotis等[4]根据滑坡的圆弧滑动模式,对抗滑桩的加固效果进行了分析;H.G.Poulos[5]根据达到要求安全系数所需抗滑力,分析每根桩所能承受的滑坡推力,并选择合适的桩型及桩数,在合适位置布桩;M.Long[6]分析了支护体系刚度对支护结构及地表位移的影响;M.Ashour等[7]基于桩土相互作用,考虑桩间距对桩身抗滑能力的影响,并对滑坡稳定系数的影响因素进行了研究;T.Ito等[8]分析了桩间距与净间距比值对滑坡加固效果及桩身安全系数的影响作用;R. Kourkoulis等[9]对产生桩身内力及位移的因素进行了分析。
为优化单根抗滑桩的受力性能,提高所有抗滑桩的整体性,可在桩顶设置连系梁。在计算理论研究方面,曾庆义等[10]提出了圈梁具有约束和协调各桩的受力和变形的作用;高印立等[11]采用弹性地基梁模型,提出了圈梁-排桩协同作用下的简化分析方法,计算圈梁、桩身二者的内力及位移;G.B.Fenelli等[12]考虑圈梁与下部抗滑结构之间具有集中力及弯矩,分析了圈梁对位移的约束作用;张志伟等[13]提出了弧形排桩-桩顶系梁空间抗滑结构的计算理论,在仅考虑连系梁与桩顶之间存在集中力时,分析了连系梁计算模型为两铰拱时的内力,以及下部抗滑桩的内力及位移。
通过阐述以上研究成果,表明桩顶连系梁可约束桩身位移,使桩的受力状态更加合理。为了降低直线连系梁的弯矩,基于拱的受力特点,可将抗滑桩呈弧形布置,桩顶设置弧形连系梁。弧形连系梁可为桩顶提供约束,使桩身内力分布趋于均匀,同时可提高抗滑桩整体性。弧形连系梁与直线连系梁相比,弯矩减小,以受压为主,能够充分发挥混凝土的抗压能力。对比弧形连系梁与直线连系梁的内力,弧形连系梁的优势较明显[13],但假设条件较多。为了使计算模型与工程实践较为吻合,笔者推导了弧形连系梁计算模型为无铰拱的内力计算公式,根据桩顶与连系梁的位移协调条件,建立抗滑结构柔度方程,并在不同的桩底约束条件下,求解桩顶与弧形连系梁之间的约束冗力,进而计算比较连系梁内力及抗滑桩内力与位移。
1 抗滑结构理论分析
1.1 抗滑结构计算模型

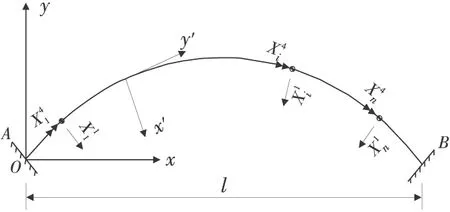
图1 连系梁计算模型平面
对连系梁建立整体坐标系oxyz,原点位于连系梁左端A,x轴为连系梁左右端部连线,以向右为正。局部坐标系px′y′z′的原点为连系梁的任一点p,第i桩顶处以i代替p,x′轴沿连系梁径向,且指向内侧为正,y′轴沿弧形连系梁切向,整体坐标系中的z轴及局部坐标系中的z′轴相互平行,均为竖直方向,以竖直向上为正。
在第i桩顶处,连系梁与桩顶之间的约束冗力分别如图2、图3。
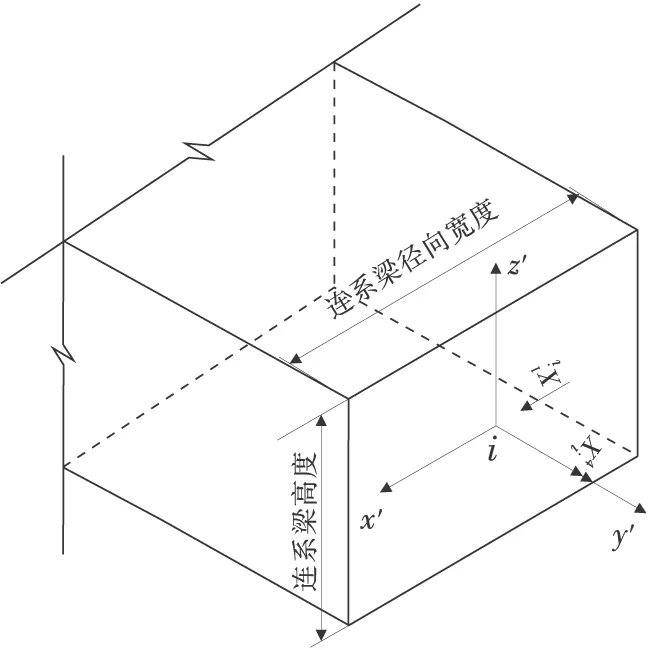
图2 i 桩顶处连系梁空间受力模型
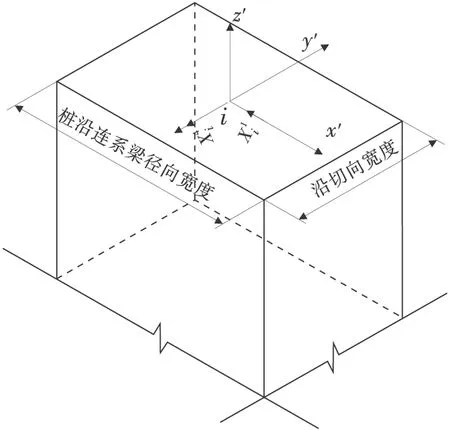
图3 i 桩顶处空间受力模型
1.2 连系梁内力分析
取B端的集中力、弯矩及扭矩为多余约束,则基本体系如图4。
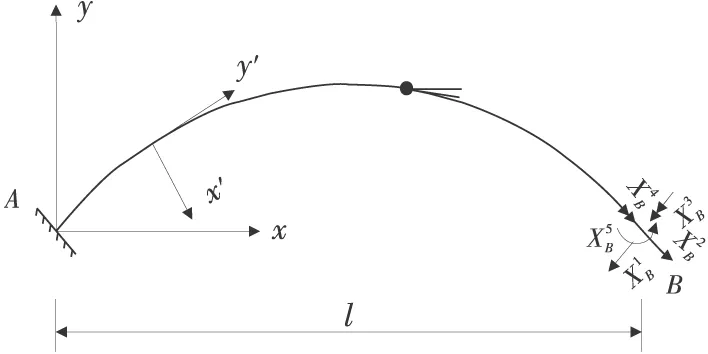
图4 无铰拱结构基本体系
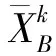
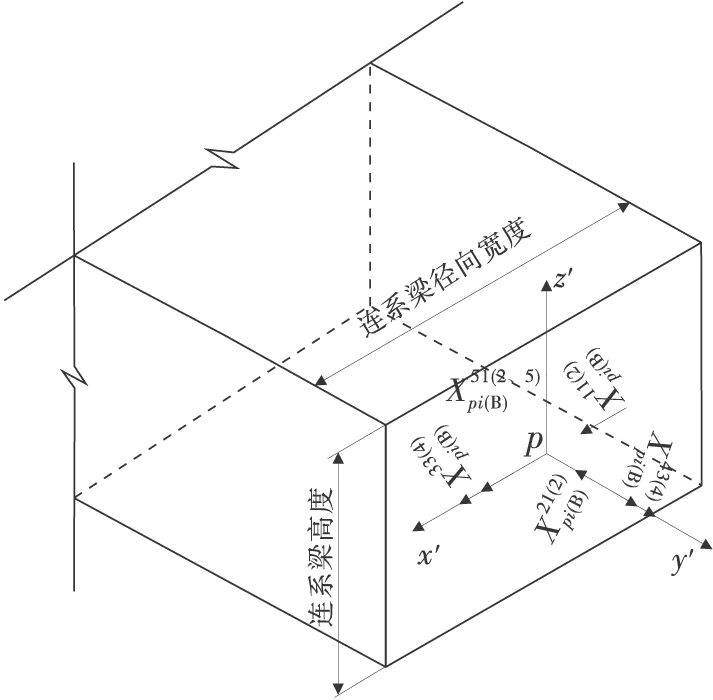
图5 连系梁任一点p内力
对p,k(m) 及j所表示的具体参数说明如下:
1)p表示在冗力作用下,产生内力的任一点,其中包括左端A。
2)k(m) 表示桩顶与连系梁间的冗力类型编号,分为5种类型(k= 1,2,3,4,5),具体对应关系如下:1为沿连系梁径向,即沿x′ 轴正方向的集中力;2为沿连系梁切向,即沿y′ 轴正方向的集中力;3为沿连系梁径向,即指向沿x′ 轴正方向的弯矩;4为沿连系梁切向,即指向沿y′ 轴正方向的扭矩;5为指向沿z′轴正方向的弯矩。
3)j表示在i(B)处冗力k(m) 作用时,p点产生的内力j,分为5种类型(j= 1,2,3,4,5),具体对应关系如下:1为点p处沿x′ 轴方向的剪力,以绕隔离体顺时针转动为正;2为点p处沿y′ 轴方向的轴力,以压力为正;3为点p处绕x′ 轴的弯矩,以系梁下侧受拉为正;4为点p处绕y′ 轴的扭矩,以指向离开截面的扭矩为正;5为点p处绕z′轴的弯矩,以使系梁内侧受拉为正。
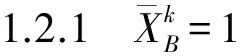
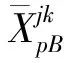
(1)
式中:φp,φB为 p 点及 B 端的切线方位角;xp为 p 点的 x 坐标;αp-B为 p 点至 B 端的坐标方位角。
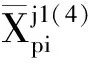
(2)
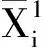
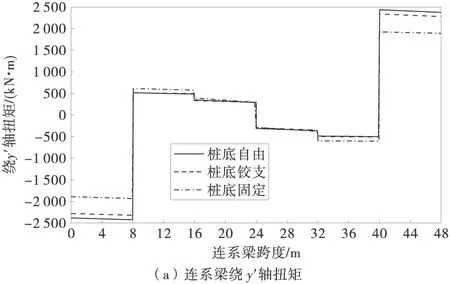
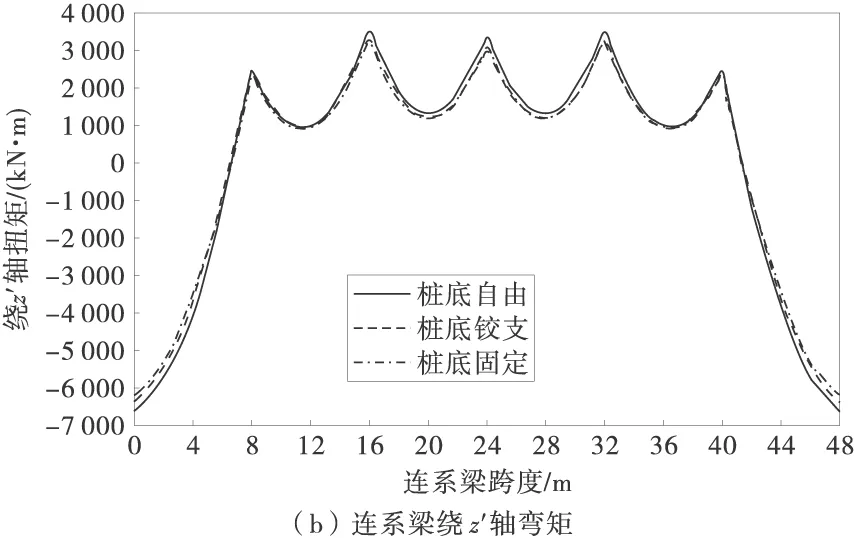
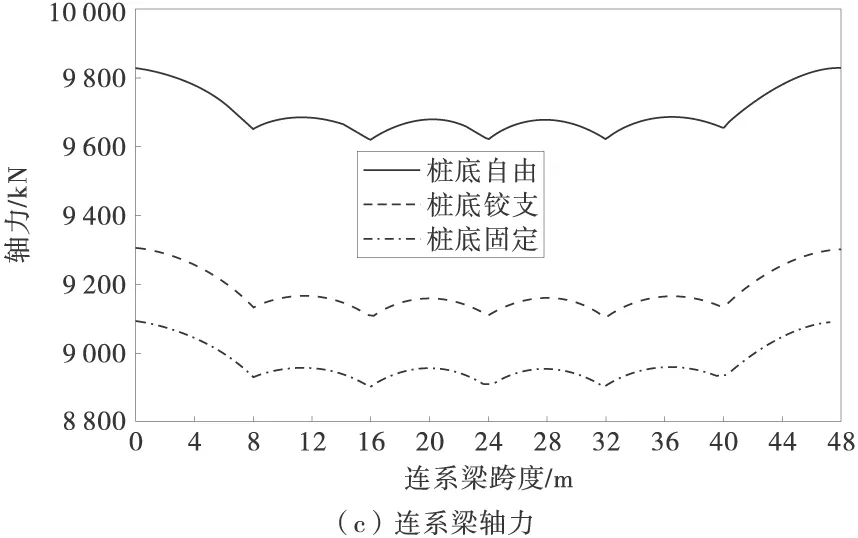
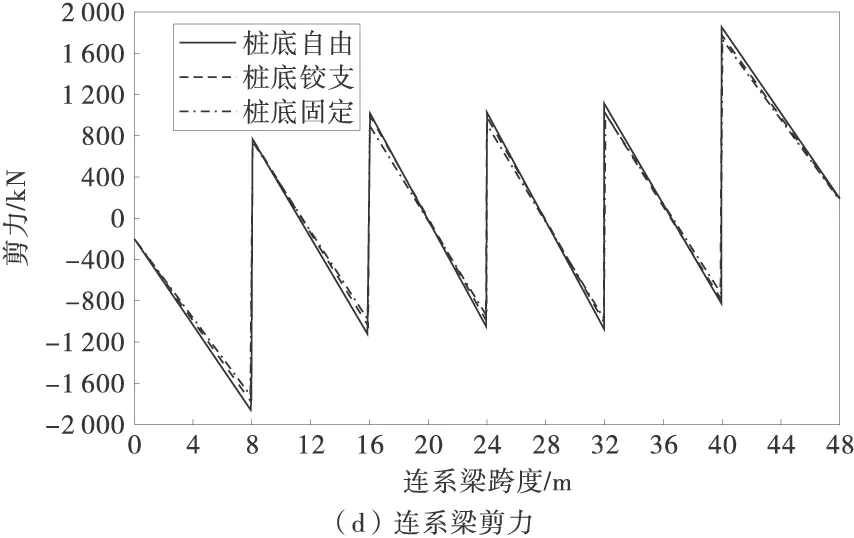
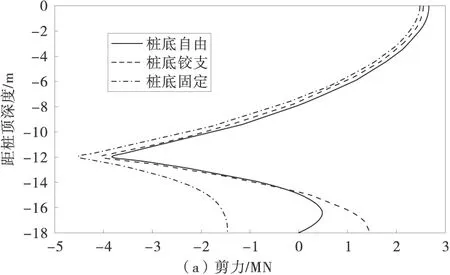
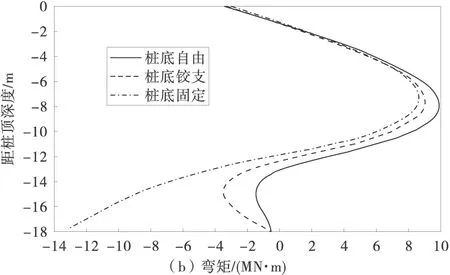
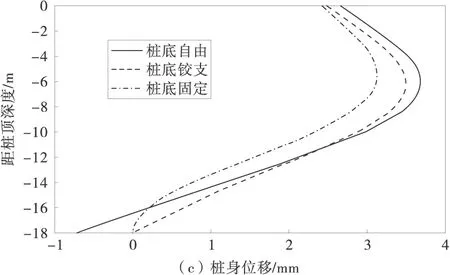
1.2.3 x1(4) (3) 1.3 抗滑桩变形分析 抗滑桩计算模型为弹性地基梁,如图6,图中 x′轴方向为连系梁径向,抗滑桩在滑动面上、下均按弹性地基梁设计,计算模型为“m-K”法。 图6 抗滑桩计算模型 根据桩底的约束条件,采用弹性桩相关的计算方法,得出第i桩顶处位移的计算表达式,如式(4): (4) 式中:vi为桩顶沿 x′轴方向位移;φi为绕 y′轴的转角;Δqx′为滑面处沿 x′轴方向按三角形分布的滑坡推力强度。 以桩底自由端为例,系数A,B,C,D,E,F具体表示如下: 式中:Ai,Bi,Di,Fi为“m”法影响函数值和“K”法影响函数值的组合系数;h1为抗滑桩受荷段长度;by′为与y′轴平行的抗滑桩边长。 同理,当桩底铰支及固定时,可通过组合分别求得系数A,B,C,D,E,F。 1.4 建立抗滑结构典型方程 利用连系梁与桩顶之间的位移协调,建立抗滑结构典型方程,如式(5): δX=v (5) 式中:δ为柔度系数矩阵;X为连系梁与桩顶连接处冗力矩阵;v为桩顶位移矩阵。 冗力X为分块矩阵,如式(6): (6) (7) 位移矩阵v为分块矩阵,如式(8): (8) (9) 式(9)中∞元素表示位移自由,即式(7)中与之对应的元素为 0,对位移无约束。 2.1 模型及计算参数选取 2.2 内力及位移分布特征 2.2.1 连系梁内力 应用MATLAB程序分别计算桩底自由、铰支及固定时,桩顶连系梁的内力,计算结果如图7。因连系梁 x′轴弯矩较小,此处忽略。 图7 连系梁内力 从图7(a)可知,在端部附近,桩底固定时,绕y′轴扭矩数值较其他两种约束情况减少约20%,主要为桩底固定时,桩顶对连系梁产生的扭矩作用减弱;因铰支和自由两种约束条件下,对桩顶弯矩的作用效果相近。所以,在铰支和自由两种约束条件下,连系梁的扭矩值比较接近。 由图7(b)可知,在端部附近,连系梁绕z′轴弯矩在桩底自由时最大,桩底固定时最小,主要为随桩底约束作用加强,桩顶对连系梁的作用力减小,在端部附近,绕z′轴弯矩数值较绕y′轴扭矩数值增大约1倍,主要为桩顶径向集中力及轴力所引起。 由图7(c)可知,桩底固定时,连系梁轴力最小,桩底自由时,连系梁轴力最大,即随桩底约束能力减弱,连系梁轴力增加,且增加效果明显。 由图7(d)可知,剪力数值约为轴力的1/5~1/4,故对连系梁混凝土的抗剪强度要求不高,且桩底约束条件对连系梁剪力分布规律基本无影响。 2.2.2 抗滑桩位移及内力 以1 # 桩为例,分别计算在不同桩底约束条件下,桩身在x′轴方向的内力及位移,计算结果如图8。 图8 1 # 桩桩身内力及位移 由图8(a)可知,在桩顶连系梁约束下,桩顶处沿x′轴方向存在剪力,3种桩底约束条件下,受荷段上半部桩身剪力基本无差别,主要为接近桩顶处以桩顶约束作用为主,随深度增加,在桩前土体抗力与滑坡推力共同作用下,桩身剪力减小,在距离桩顶2/3受荷段处,产生反向剪力,并持续增大至滑面处;在锚固段,随深度增加,土体锚固作用增强,不同的桩底约束条件对桩身剪力的影响逐渐显明,桩底自由时,剪力减小至0;铰支条件下,剪力逐渐减小并产生与固定条件下方向相反的剪力,但数值与固定条件下基本相同,主要为固定与铰支两种约束条件对桩底附近的剪力作用效果基本相同,但约束方向相反。 由图8(b)可知,在连系梁约束下,桩顶产生绕x′轴方向的弯矩,对比3种桩底约束条件,受荷段上半部桩身弯矩随深度增加,滑坡推力增加而增大,但三者数值比较接近,在受荷段下半部,因桩前土体抗力逐渐发挥作用,桩身弯矩减小,随桩底约束条件不同,桩底固定时最小,桩底自由时最大;在锚固段,土体锚固作用已充分体现,桩底固定条件下桩身产生反向弯矩,并持续增大,在桩底处弯矩数值超过正向最大弯矩,而桩底自由及铰支条件下,桩身弯矩逐渐减小至0,且在反向弯矩区段,弯矩数值在桩底铰支条件下较桩底自由条件时大。 由图8(c)可知,在桩身受荷段,桩底固定条件下沿x′轴方向位移最小,在桩底自由时最大;在受荷段上半部,位移随深度增加而增大,在下半部位移减小,由位移曲线可知,连系梁对受荷段上半部桩身位移起到了较好的约束作用;在锚固段,桩底自由时位移减小效果明,在桩底附近产生约为受荷段最大位移1/4的反向位移。 1)推导了弧形连系梁计算模型为无铰拱的内力计算公式,并在不同桩底约束条件下,计算了弧形连系梁的内力及抗滑桩内力和位移。 2)桩底约束条件影响弧形连系梁的内力分布规律,尤其对轴力影响效果明显,随桩底约束能力减弱,轴力增加,可通过减小锚固段长度,充分利用连系梁混凝土的抗压性能。 3)在桩顶连系梁约束下,桩底约束条件对桩身剪力及弯矩影响效果明显,桩底固定时,桩底部弯矩较大;而桩底自由时,弯矩明显减小,而通过连系梁的约束作用,桩身位移增加亦在允许范围之内,在桩顶连系梁的约束作用下,如适当减小锚固段长度,能够减小桩底部桩身弯矩,并可降低工程造价。 [1] 罗伟,李亮,赵炼恒,等.临河岩石边坡抗滑稳定性分析[J].公路交通科技,2013,30(8):23-28,42. Luo Wei,Li Liang,Zhao Lianheng,et al.Study on anti-slide stability of rock slope along river[J].Journal of Highway and Transportation Research and Development,2013,30(8):23-28,42. [2] 王恭先.滑坡防治中的关键技术及其处理方法[J].岩石力学与工程学报,2005,24 (21):20-29. Wang Gongxian.Key technique in landslide control and its handling measures[J].Chinese Journal of Rock Mechanics and Engineering,2005,24 (21):20-29. [3] 贺建清,张家生,梅松华.弹性抗滑桩设计中几个问题的探讨[J].岩石力学与工程学报,1999,18(5):600-602. He Jianqing,Zhang Jiansheng,Mei Songhua.Inquiring into some questions in anti-slide pile[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(5):600-602. [4] Hassiotis S,Chameau J,Gunaratne M.Design method for stabilization of slopes with piles[J].Journal of Geotechnical and Geoenvironmental Engineering,1997,123(4): 314-323. [5] Poulos H G.Design of reinforcing piles to increase slope stability [J].Canadian Geotechnical Journal,1995,32(5): 808-818. [6] Long M.Database for retaining wall and ground movements due to deep excavations [J].Journal of Geotechnical and Geoenvironmental Engineering,2001,127(3): 203-224. [7] Ashour M,Ardalan H.Analysis of pile stabilized slopes based on soil-pile interaction[J].Computers and Geotechnics,2012,39: 85-97. [8] Ito T,Matsui T,Hong W P.Extended design method for multi-row stabilizing piles against landslide [J].Soils and Foundations,1982,22(1): 1-13. [9] Kourkoulis R,Gelagoti F,Anastasopoulos I,et al.Slope stabilizing piles and pile-groups: Parametric study and design insights[J].Journal of Geotechnical and Geoenvironmental Engineering,2011,137(7): 663-677. [10] 曾庆义,刘明成.支护桩圈梁的作用机理与计算分析[J].岩土力学,1995,16(2):74-82. Zeng Qingyi,Liu Mingcheng.Mechanism and calculating analysis for ring beam of soldier piles [J].Rock and Soil Mechanics,1995,16(2): 74-82. [11] 高印立,徐建新,陈环.排桩与圈梁协同作用下考虑开挖过程的挠曲方程法[J].土木工程学报,2001,34(1):67-72. Gao Yinli,Xu Jianxin,Chen Huan.A flexing equation method considering the cooperative action between row of piles and ring beam during excavation procedure [J].China Civil Engineering Journal,2001,34(1):67-72. [12] Fenelli G B,Pagano L.Computing top-beam effects in retaining walls[J].Journal of Geotechnical and Geoenvironmental Engineering,1999,125(8): 665-672. [13] 张志伟,邓荣贵.弧形间隔排桩-桩顶拱梁空间抗滑结构理论研究[J].岩土力学,2013,34(12):3403-3409,3430. Zhang Zhiwei,Deng Ronggui.Theoretical study on spatial anti-slide structure of arc interval row piles with coupling beam on the pile top[J].Rock and Soil Mechanics,2013,34(12): 3403-3409,3430. Study on the Effect of Different Constraint Condition at Pile Bottom on Internal Force Distribution of Arc Row Piles with Arc Coupling Beam Zhang Zhiwei,Deng Ronggui,Wang Zhenyong,Zhong Zhibin (School of Civil Engineering,Southwest Jiaotong University,Chengdu 610031,Sichuan,China) The model for arc coupling beam can be simplified as hingeless arch, according to the high order statically indeterminate characteristics of the spatial anti-slide structure, with the redundant forces between beam and pile top, by using deformation compatibility to set up flexibility equation of new spatial anti-slide structure. Based on the different constraint conditions such as freedom, hinge and fixation at the pile bottom to solve the redundant forces, then calculate and compare the internal force of arc coupling beam and the internal force and displacement of pile among the different constraint conditions at the pile bottom, and the influence law of internal force and displacement by different constraint conditions was obtained. That the moment at the bottom of pile is larger as fixed, but reduce obviously as free and displacement increase. By the constraint of coupling beam, shortening the length of anchoring section can reduce the moment at the bottom of pile. geotechnical engineering; anti-slide structure; arc row piles; arc coupling beam; constraint of pile bottom; internal force distribution 10.3969/j.issn.1674-0696.2015.04.15 2014-04-04; 2015-03-27 国家自然科学基金项目(41272321);高等学校博士学科点专项科研基金项目(20120184110023) 张志伟(1979—),男,吉林长春人,博士研究生,主要从事边坡及滑坡治理方面的研究。E-mail:zwzhangswjtu@163.com。 TU753.3 A 1674-0696(2015)04-081-06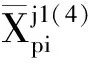
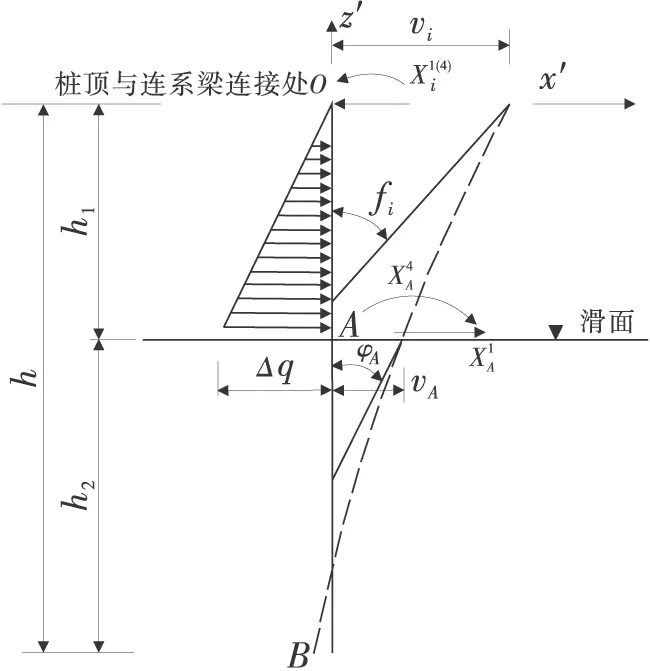
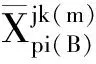
2 算例分析与讨论
3 结 论
