基于路面不平整度的车辆动荷载系数分析
2015-06-07杨春风孙吉书
杨春风,解 帅,孙吉书
(河北工业大学 土木工程学院,天津 300401)
基于路面不平整度的车辆动荷载系数分析
杨春风,解 帅,孙吉书
(河北工业大学 土木工程学院,天津 300401)
为更好地研究路面不平整度下车辆对路面的动载作用,运用1/4车辆振动模型,借助MATLAB数学计算软件,分析路面不平整度、车辆参数等因素对动载系数的影响规律。结果表明:车速、路面振幅对动载系数影响很大,路面振幅与动载系数呈线性关系,验证了路面不平整是导致动载的主要原因;汽车结构参数中的轮胎阻尼、悬架刚度、悬架阻尼对动载系数影响较小,但减小轮胎刚度可以显著地减小动载。从道路设计的角度考虑,提高道路的平整度是减小动载的重要措施。
道路工程;振动模型;车辆参数;动载系数
0 引 言
车辆在路面上行驶,是一个车路相互作用的过程。由于道路的不平整和车辆自身的振动,造成车辆对路面产生不可避免的动载作用,这个作用远大于道路设计规范中的静载,它在破坏道路的同时也会影响驾驶的安全性和舒适度,最终形成恶性循环,大大降低了道路使用寿命。
目前,国内外一些专家学者开始研究车辆荷载对路面结构的动态作用。D. Cebon[1]研究了车辆结构对胎压和路面的动态影响,并做了一些优化设计;R.V.Siddharthan等[2]利用傅立叶变换的有限元计算方法,基于轮胎和路面的接触,模拟了实际移动荷载对路面的力学作用;日本的寺择宽一运用贝塞尔函数,在弹性半空间体的轴对称作用下,推导了计算路面位移和应力的函数计算式。国内最早开始研究路面动力学的是邓学钧和孙璐[3],他们利用车辆对地面结构随机的振动,研究了各种运动荷载下的路面结构力学响应;叶开沅等[4]考虑在动载质量、惯性力及阻尼作用下,研究了车辆通过连续梁时的振动过程,并得出了任意运动荷载作用下连续梁的动力解析解;为减小动荷载,余卓平等[5]对车辆的优化设计了汽车悬架,并提出减小路面损伤的方法;王直民等[6]分析了车辆动荷载系数的概率分布,运用疲劳损伤理论得出了不平整路面上等效动荷载的表达式;舒富民等[7]研究了移动荷载作用下路面力学指标响应结果,分析了车速对各力学指标的影响规律;陈俊等[8]建立路面结构的离散元模型,模拟了静止、振动和移动荷载对路面结构的作用,并分析出了不同荷载形式下路面结构的力学响应。
综上所述,现有研究多数围绕动载对路面结构的动态力学响应,未考虑影响动载作用大小的动载系数,笔者运用车辆-路面振动模型,推导车辆动荷载系数表达式,利用MATLAB数学分析软件,计算振动矩阵方程,分析了在不同路面振幅、波长下,最大动载系数的变化规律,研究了悬架系统和轮胎刚度、阻尼对动载系数的影响。
1 产生动载的原因
振动,是车辆对路面产生动载的先决条件,而车辆实际行驶过程中产生振动是不可避免的。车辆的振动不仅会降低乘客的舒适度和安全性,同时也会增加汽车零部件的磨损及行驶燃料的损耗,最终由车辆振动产生的动载又会作用在路面上,进一步加剧路面的破坏。车辆行驶的过程,实质上是一个车辆与路面相互作用的过程,动荷载产生的原因也主要来自车辆和路面这两个方面。一方面由于路面的不平整导致车辆产生各个方向的振动,振动主要为垂直路面方向;另一方面,车辆自身的振动。车辆内部的发动机的振动会引起车身间歇性振动。
2 动载系数表达式的建立
2.1 1/4车辆振动模型
在实际中,车辆是一个多自由度的复杂振动系统,所以建立车辆模型的自由度越多,模拟出的运动状态就越真实。车辆是由一系列具有质量、刚度和阻尼特性元件的组合。为简化计算,采用二自由度的1/4车辆模型作为振动模型,该模型只考虑车辆的竖向运动,即非悬架和悬架系统的竖向振动,忽略了其他各向的运动,如图1。

图1 1/4车辆振动模型
图1中:m1为非悬架质量;m2为悬架质量;k1为非悬架刚度;k2为悬架刚度;c1为非悬架阻尼;c2为悬架阻尼;y1为非悬架垂直位移;y2为悬架垂直位移;y0为路面对车辆的激励,即路面平整度函数。其运动微分方程为:

(1)
或:
(2)
式中:M为质量矩阵;C为阻尼矩阵;K为刚度矩阵;Y为位移列阵;f(t)为荷载列阵。
2.2 求解振动方程
东,表示日出的方向,与“西”相对,诗云:“嚖彼小星,三五在東。”(《诗·召南·小星》)西,则表示日落的方向,“自西徂東,靡所定處。”(《诗·大雅·桑柔》)“东西”最早出现时也表示方位,与“南北”相呼应。

则:
(3)
利用待定系数法,设:
(4)
现阶段对于路面平整度的表达,普遍采用MW. Sayers的正弦波路面表示方法,因此路面波形函数为:
y0=hsin(ωt)
(5)
式中:h为路面不平整度,即正弦波函数的振幅;ω为频率,与车速和路面不平整度波长有关。
将z1,z2,y0带入式(3)可写成矩阵形式:
利用MATLAB求解器计算上面的矩阵方程,可以得出A1和A2,带入式(4)得到z1,则车轮对路面的动荷载表达式为:
(6)
其中:
θ=tan-1(A1/A3)
当正弦函数sin(ωt+φ)=1时,pd得到最大值:
(7)
最终可以得出动荷载系数D:
式中:P0为车辆静载,通常为(m1+m2)g。
3 动荷载系数的求解和分析
以中型标准车辆为分析对象,带入车辆结构参数,通过MATLAB数学分析软件,计算动载系数,分析路面不平整度、车辆参数等因素对最大动荷载系数的影响规律。标准车辆结构参数如表1。

表1 车辆结构参数
3.1 车速、路面不平整度对动荷载系数影响规律
如图2,随车速的增加,动荷载系数先减小后增大,到达峰值后略微下降。车辆在20~40 km/h低速行驶时,动荷载系数较小,主要在1.1~1.2范围内变化,超过40 km/h后,动荷载系数大幅增加,大约110 km/h时,动荷载系数达到最大值1.47。可见,车速的变化对于动荷载系数的影响较大,应根据道路等级合理选取速度区间。

图2 动荷载系数与车速的变化关系曲线
由图3可以看出,随着路面波长的不断变大,动荷载系数呈现两个波峰。第1个波峰的峰值略大于第2个波峰,当波长较小时,动荷载系数的第1个峰值可以达到最大值1.5。图3有40,80,120 km/h 三个速度下的变化曲线,均呈现上述特征,而且速度的变化对动荷载系数的峰值影响很小。当波长增大到某一程度,可以当作路面趋于平整,此时动荷载系数接近于1。
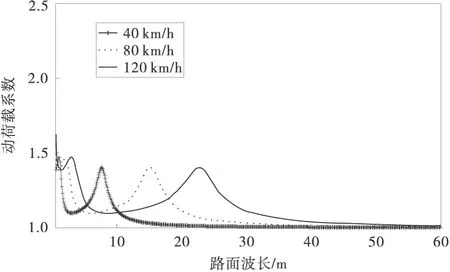
图3 动载系数与路面波长变化关系曲线
图4分别取车速为40,80,120 km/h,在不平整度由小到大依次变化。车速一定时,随着路面振幅的增大,动荷载系数呈线性递增,这与实际经验相符,所以路面不平整度的幅值对动荷载系数的影响很大,控制路面平整度是减小动载的重要途径。当振幅一定时,速度较大的,动荷载系数也变大,观察曲线可以看出,速度大的,动荷载系数增速较快,这可以看作由路面不平整度所引起的振动与车辆自身振动相耦合,也就是说,速度变大会加剧车辆的振动,最终导致动荷载系数大大增加。
当实际路面状况较差时,根据车速对动荷载系数的影响分析,应及时对该路段进行修补和交通管制,限制车辆行驶速度,不仅可以降低路面损坏程度,也提高了车辆行驶的安全性。
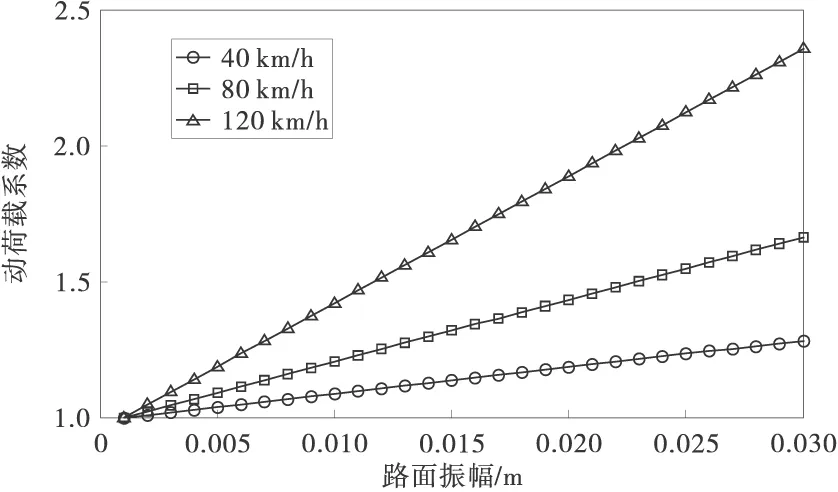
图4 动荷载系数与路面振幅的变化关系曲线
随着路面振幅的增大,动荷载系数呈线性递增,这与实际经验相符,从图4可以看出,路面不平整度的幅值对动荷载系数的影响很大,所以控制路面平整度是减小动载的重要途径。速度较大时,动荷载系数变化幅度增大,这可以看作由路面不平整度所引起的振动与车辆自身振动相耦合,也就是说,速度变大会加剧车辆的振动,导致动荷载系数大大增加。
3.2 车辆参数对动荷载系数的影响规律
由于车辆参数的影响因素较多,所以选取路面波长为3 m,路面振幅为0.01 m作为路面不平度条件作为前提,逐一分析各车辆参数对动荷载系数的变化规律。图5是轮胎刚度对动荷载系数的影响规律。动荷载系数随着轮胎刚度递增,并且数值变化较大,当轮胎刚度增加70%时,动荷载系数会提高30%;而与上述过程截然相反的是,随着轮胎阻尼的增大,动荷载系数会降低,但是影响的程度很小。如图6轮胎阻尼从4 kN·s/m增大到8 kN·s/m,动荷载系数只变化了3%。
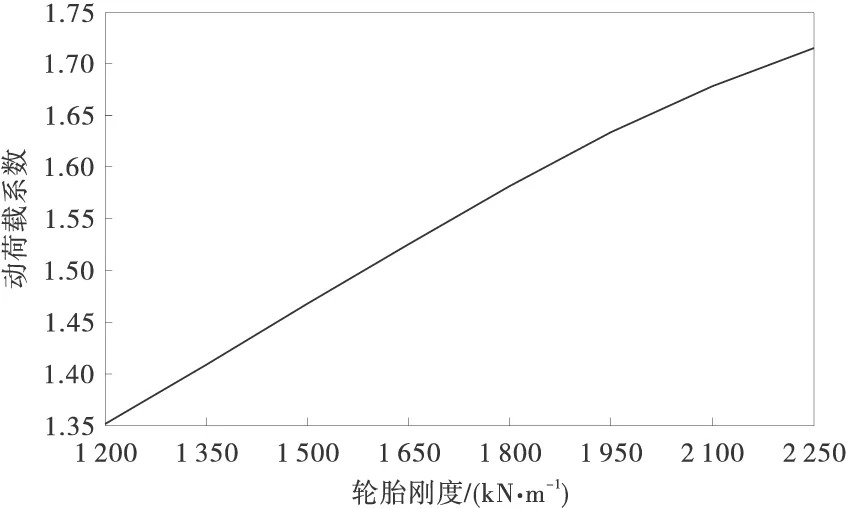
图5 动荷载系数与轮胎刚度的变化关系曲线
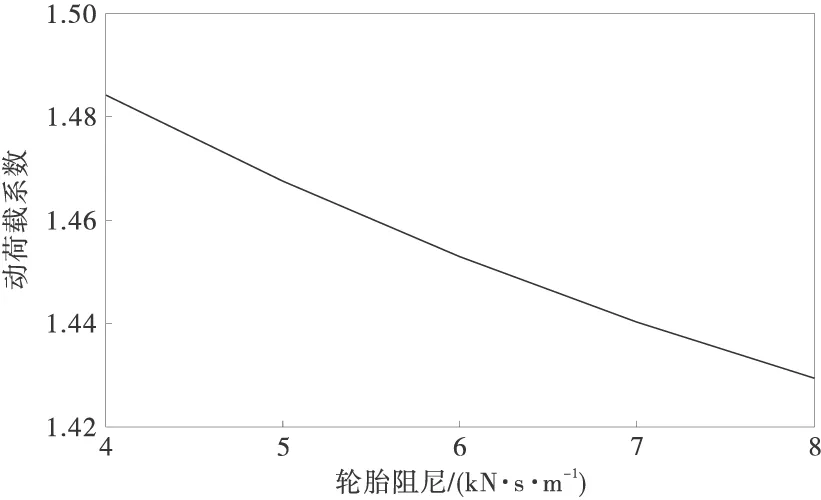
图6 动荷载系数与轮胎阻尼的变化关系曲线
图7和图8是悬架刚度和阻尼对动荷载系数的影响变化规律。很明显,随着悬架刚度和阻尼的增大,动荷载系数均减小。当悬架刚度和阻尼增加200%,动荷载系数分别降低了4%和5%,可见增加悬架的刚度和阻尼可以降低动荷载系数,减小车辆运行的振动,但是影响程度很小。

图7 动荷载系数与悬架刚度的变化关系曲线
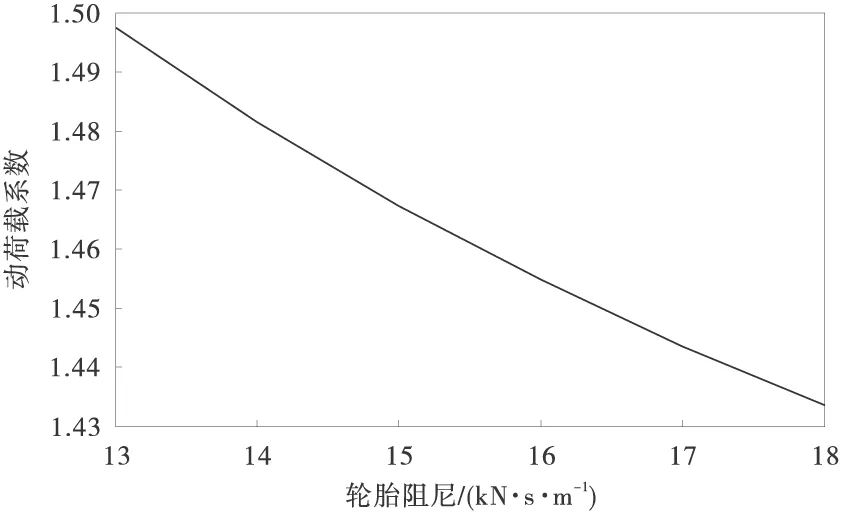
图8 动荷载系数与悬架阻尼的变化关系曲线
在运行速度为80 km/h,车辆空载、满载、超载10%,20%,30%,40%,50%,60%,70%,80%的条件下,计算动荷载系数的变化,如图9车辆空载的动载系数较满载时高10%左右,车辆振动较剧烈。随着载重不断增大,动荷载系数也逐渐减小。虽然在一定程度下,载重的增加可以减小动荷载系数,但是车辆静载和附加动载总和会变大,对路面的冲击力仍会大幅提高,路面很有可能产生严重的结构性破坏。所以,车辆应严禁超载,防止路面损害。
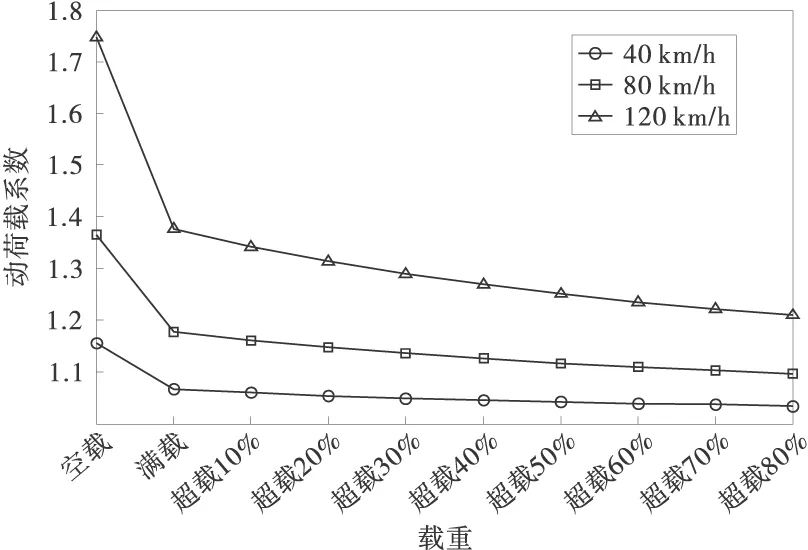
图9 动荷载系数与载重的变化关系曲线
根据实际路面状况,取中型标准车的结构参数,当路面不平整度h=0.02 m,路面波长为3 m,车速为80 km/h下,求出最大动荷载系数参考值为1.46,该值比普遍认为的1.3~1.4较大。当路面不平整度较差时,动载可以达到静载的2倍、甚至3倍以上,所以当路面出现损坏时,必须及时修补或者采取交通管制,否则可能为道路、行车安全带来重大隐患。
4 结 论
1)车辆在行驶过程中,由于路面不平整而产生对路面的附加荷载,这正是车路相互作用的结果。根据沥青路面的特点,以正弦波形路面作为激励,利用四分之一车辆振动模型,建立了车辆-路面动载系数计算模型。
2)以标准车辆为对象,通过MATLAB数学计算软件,研究路面平整度、车速、载重及车辆参数对动荷载系数的影响规律。当车速较低时动荷载系数较小,速度超过40 km/h时动荷载系数与车速呈线性增长关系,速度达到110 km/h时,动荷载系数达到峰值;路面振幅对动荷载系数影响较大,这验证了路面不平整是引起动荷载的主要原因。由于车速耦合作用明显,当路面状况较差时,应降低车速,及时修补,避免加剧路面的损坏。
3)轮胎刚度对动荷载系数影响较大,适当降低轮胎刚度可以减小动荷载系数。轮胎阻尼、悬架刚度、悬架阻尼的提高均可降低动荷载系数,但影响程度较小,可根据车辆构造,合理选取车辆结构参数。
4)根据实际道路状况,动荷载系数基本在1.4~1.5范围内,但出道路损坏时,动荷载系数将成倍增长。严格控制路面平整度是减小动荷载和道路损坏,提高道路使用寿命的重要途径。
[1] Cebon D.Theretical road damage due to dynamic tire forces of heavy vehicles [J].Journal of Mechanical Engineering Science,1988,202(2):103-117.
[2] Siddharthan R V,Krishnamenon N,El-Mously Mohey,et al.Investigation of tire contact stress distributions on pavement response [J] .Journal of Transportation Engineering,2002,128(2):136-144.
[3] 邓学钧,孙璐.车辆-地面结构系统动力学[M].北京:人民交通出版社,2000. Deng Xuejun,Sun Lu.Dynamics of Vehicle-Ground Pavement Structure System [M].Beijing:China Communications Press,2000.
[4] 叶开沅,马国琳.行动载荷作用下的连续梁的横向振动问题[J].应用数学和力学,1985,6(10):873-878. Ye Kaiyuan,Ma Guolin.Vibration theory of continuous beam under the action of moving load [J].Applied Mathematics and Mechanics,1985,6(10):873-878.
[5] 余卓平,黄锡朋,张洪欣.减轻重型汽车对道路的损伤-汽车悬架优化设计[J].中国公路学报,1994,7(3):83-87. Yu Zhouping,Huang Xipeng,Zhang Hongxin.The alleviation of damage to road by heavy vehicle optimization design of vehicle suspension [J].China Journal of Highway and Transport,1994,7(3):83-87
[6] 王直民,张土乔,吴小刚.不平整路面上的车辆等效动载系数[J].浙江大学学报:工学版,2007,41(6):1007-1011. Wang Zhimin,Zhang Tuqiao,Wu Xiaogang .Equivalent vehicle dynamic load coefficient on rough pavement [J].Journal of Zhejiang University:Engineering Science,2007,41(6):1007-1011.
[7] 舒富民,钱振东.移动荷载作用下沥青路面的动力响应分析[J].交通运输工程与信息学报,2007,5(3):90-95. Shu Fumin,Qian Zhendong.Analysis on the dynamic response of asphalt pavement under moving Load [J].Journal of Transportation Engineering and Information,2007,5(3):90-95.
[8] 陈俊,黄晓明,汪林兵,等.移动荷载作用下柔性路面多尺度结构的响应[J].东南大学学报:英文版,2013,29(4):425-430. Chen Jun,Huang Xiaoming,Wang Linbing,et al.Dynamic response of multi-scale structure in flexible pavement to moving load [J].Journal of Southeast University:English Edition,2013,29(4):425-430.
Vehicle Dynamic Load Coefficient Analysis Based on Pavement Roughness
Yang Chunfeng, Xie Shuai, Sun Jishu
(School of Civil Engineering, Hebei University of Technology, Tianjin 300401, China)
In order to study the dynamic load effect of vehicle running on uneven pavement further, a quarter-vehicle vibration model was applied to analyze the influence law of dynamic load coefficient based on the pavement roughness, vehicle parameters and other factors by using MATLAB software. Calculation result indicates that speed and the road surface amplitude have a great influence on the dynamic load coefficient, and pavement amplitude has a linear relationship with dynamic load coefficient. It is also indicated that the main cause of the dynamic load is pavement roughness; tire damping, suspension stiffness and suspension damping have less impact on the dynamic load coefficient than others, meanwhile, to reduce the tire stiffness can significantly reduce the dynamic load. From the view point of road design, to improve the road roughness is an important measure to reduce the dynamic load.
road engineering; vibration model; vehicle parameters; dynamic load coefficient
10.3969/j.issn.1674-0696.2015.04.14
2014-04-23;
2014-10-14
河北省高等学校科学研究计划项目(Q2012156)
杨春风(1959—),男,天津蓟县人,教授,主要从事道路工程方面的研究。E-mail:cfy211@163.com。
U416.217
A
1674-0696(2015)04-077-04
