跳扩散模型下的两种奇异期权定价

周双娇

(南京财经大学应用数学学院，江苏南京210046)

跳扩散模型下的两种奇异期权定价

周双娇

(南京财经大学应用数学学院，江苏南京210046)

假定股票价格的跳过程为一类特殊的更新过程，建立随机利率下带多个跳源的跳扩散模型，利用等价鞅测度变换方法，推导出两种奇异期权的定价公式.

更新过程;随机利率;鞅方法;奇异期权

1 引言

随着期权定价理论的不断发展，越来越多的模型应用于各式各样的期权定价中.1973年，Black和Scholes［1］提出了著名的期权定价模型，1976年Merton［2］引入跳扩散模型，其跳过程为Poisson过程.宁丽娟［3］(2003)将跳过程推广为比Poisson过程更为一般的一种特殊的更新过程，推导欧式期权定价公式.颜玲等［4］(2012)讨论了有多个跳源的跳扩散模型的期权定价.本文建立随机利率下带多个跳源的跳扩散模型，其中跳过程为一类特殊的更新过程，通过两次测度变换，分别给出了上限型权证和抵付型权证的定价公式.

2 预备知识

定义1［3］(T1)i≥0是一列独立同服从Γ分布Γ(α，λ)(α＞0，λ＞0)的随机变量序列.令则计数过程N(t)=sup{n∶τn≤t}为一类特殊的更新过程.

引理1［3］若{N(t)，t≥0}是定义1的一类特殊的更新过程，记Pn(t)=P(N(t)=n)，则

当α为正整数时，

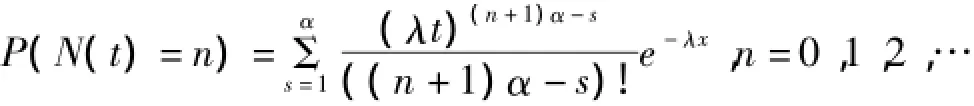
特别地，当α=1时，

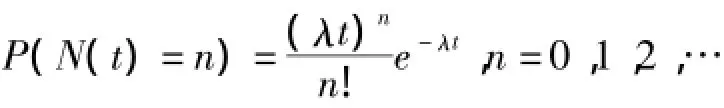
引理2［5］若W1(t)，W2(t)是测度Q下的标准Brown运动，且dW1(t)dW2(t)=ρdt，其中ρ为常数，则是Q下的标准Brown运动，其中e1(s)，e1(s)(s∈［0，T］)是确定性的可积函数.

引理3［6］若X～N(μ，σ2)，则

根据引理3，易得以下推论:

推论1在引理3的条件下，有

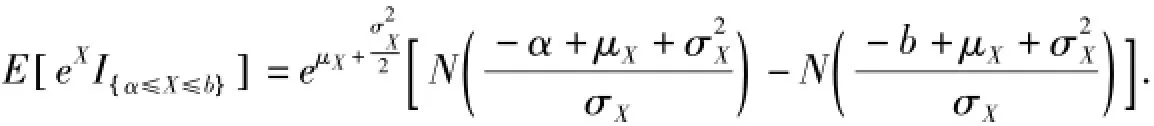
3 模型假设

假设市场是一个无套利、无税收、无交易成本、无摩擦、可连续交易的完全金融市场.该市场中仅有两种资产，一种是风险资产(股票)St，另一种是无风险资产(债券)B(t，T)，在风险中性概率空间(Ω，F，P)中，其价格分别满足一下随机微分方程:

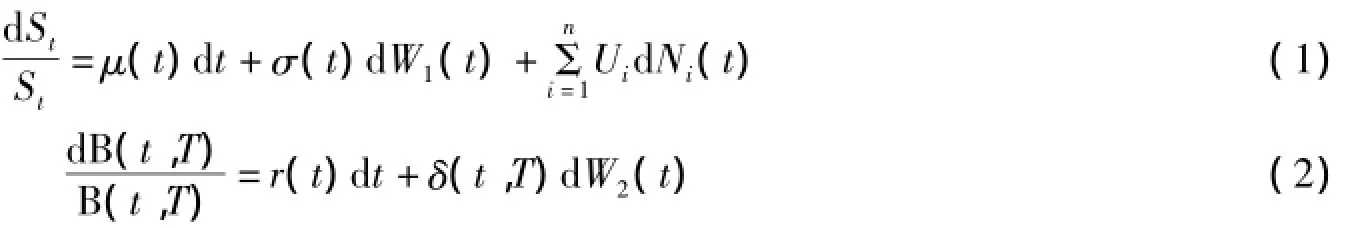
其中μ(t)为股票的预期收益率;r(t)为可能随机的短期利率;σ(t)无跳时股票价格的波动率;W1(t)，W2(t)为概率空间(Ω，F，P)上的标准布朗运动，且ρ(W1(t)，W1(t))=ρ，0≤ρ≤1.Ni(t)是股票价格过程St在t时刻发生第i种跳跃的计数过程，为定义1所述的一种特殊的更新过程，强度为，且N1(t)，N2(t)，…，Nn(t)相互独立.(Ui)i≥0(Ui＞－1)为随机变量，是股票价格发生跳跃时股票价格的相对跳跃高度，且1n(1+Ui)服从正态分布，其中hi为Ui的无条件期望，即hi=E (Ui)，v2i为1n(1+Ui)的方差.设(Ui)i≥0，Ni(t)与W1(t)，W2(t)相互独立.这里S(0)=S0，B(T，T)=1.

4 期权定价

4.1 上限型权证

定义2上限型权证或买权到期时的价值或现金流量为:

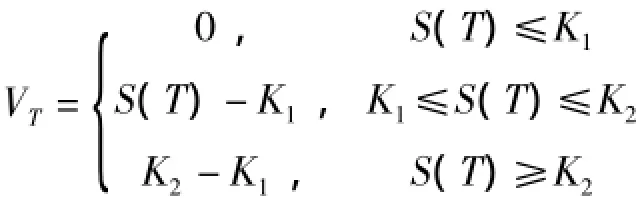
其中K1＜K2给定.

定理1股票价格过程S(t)和债券价格过程B(t，T)分别满足随机微分方程(1)、(2)，则到期日为T的上限型权证在0时刻的定价公式为:

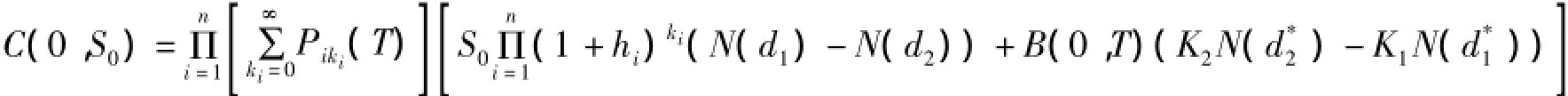
其中，

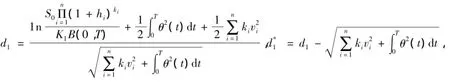
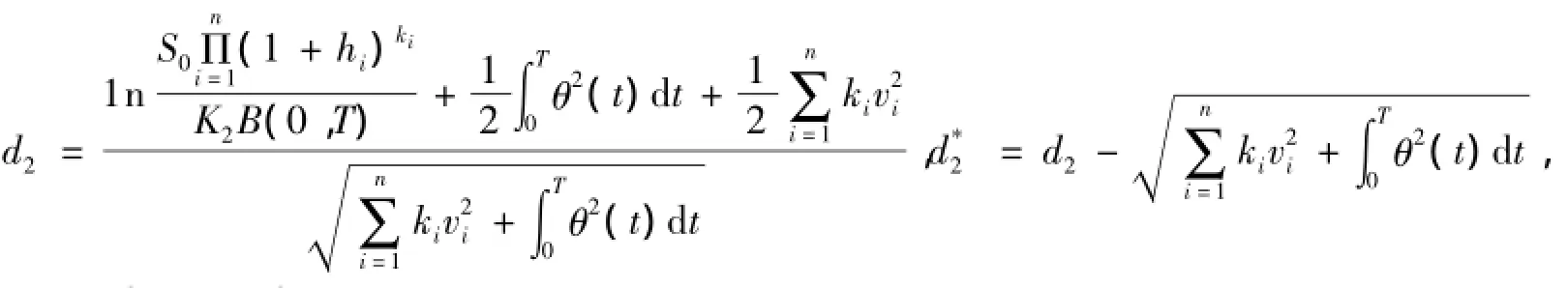
θ2(t)=σ2(t)+δ2(t，T)－2ρσ(t)δ(t，T)，且N(·)为标准正态分布的累积分布函数.

证明:设股票价格过程S(t)和债券价格过程B(t，T)分别满足随机微分方程(1)，(2).利用由Girsanov定理构造一个等价鞅测度:

则P*是与P等价的鞅测度，且为测度P*下的标准Brown运动，于是(1)式变为

由It^o公式得:

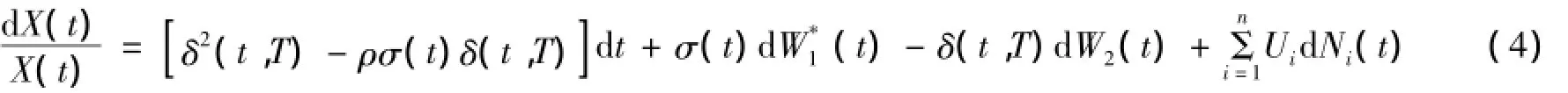
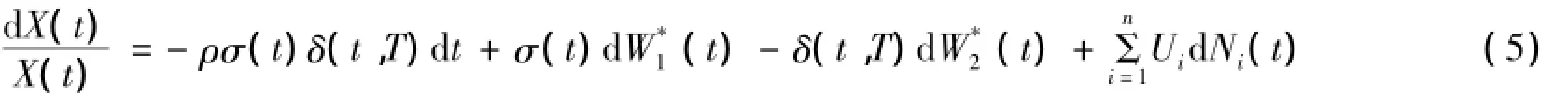
由引理1和文献［5］可知:~W2(t)为测度Q下的标准Brown运动.

则(5)式简化为:

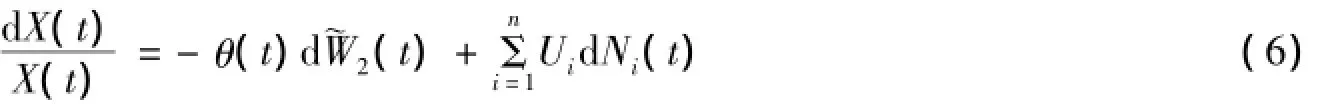
对给定的ki(i=1，2，…，n)，有

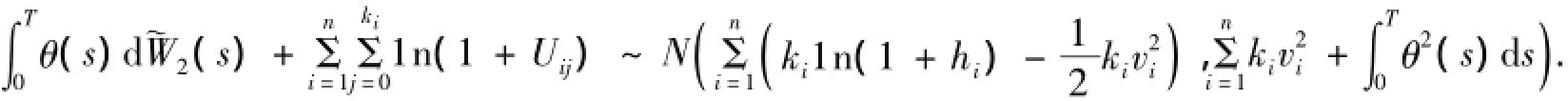
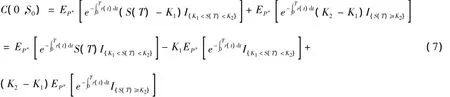
先算I1，根据全期望公式和推论1，有:

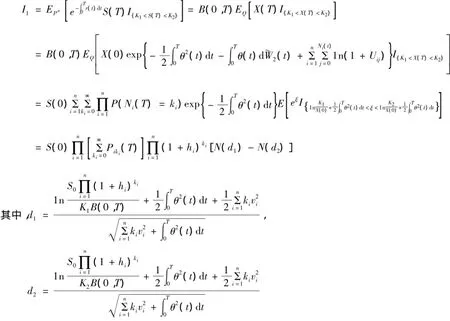
同理，再算I2:

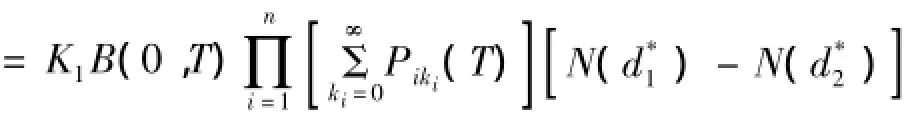
同理可得:

将I1，I2，I3分别代入(7)式化简得:

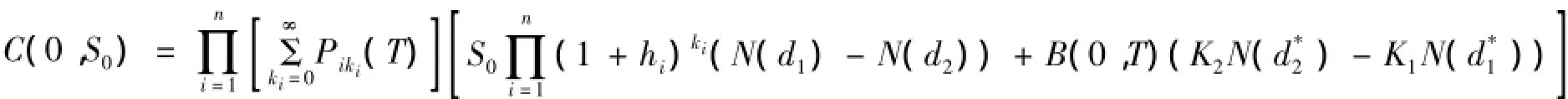
将上述定理中的0时刻改为t时刻，用类似的方法可以得到以下推论:

推论2股票价格过程S(t)和债券价格过程B(t，T)分别满足随机微分方程(1)、(2)，则到期日为T的上限型权证在t时刻的定价公式为:

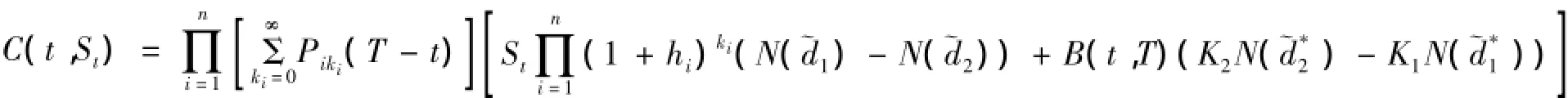
其中，

θ2(t)=σ2(t)+δ2(t，T)－2ρσ(t)δ(t，T)，N(·)为标准正态分布的累积分布函数.

4.2 抵付型权证

定义3抵付型权证或卖权到期时的价值或现金流量为:

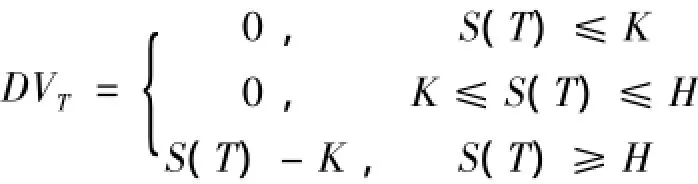
其中K为履约价格.

运用与定理1类似的方法可以得到以下定理:

定理2股票价格过程S(t)和债券价格过程B(t，T)分别满足随机微分方程(1)、(2)，则到期日为T的抵付型权证在0时刻的定价公式为:

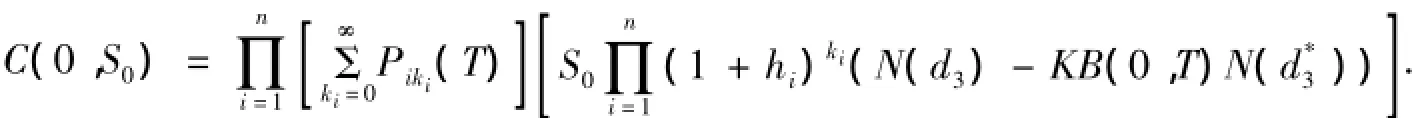
其中，

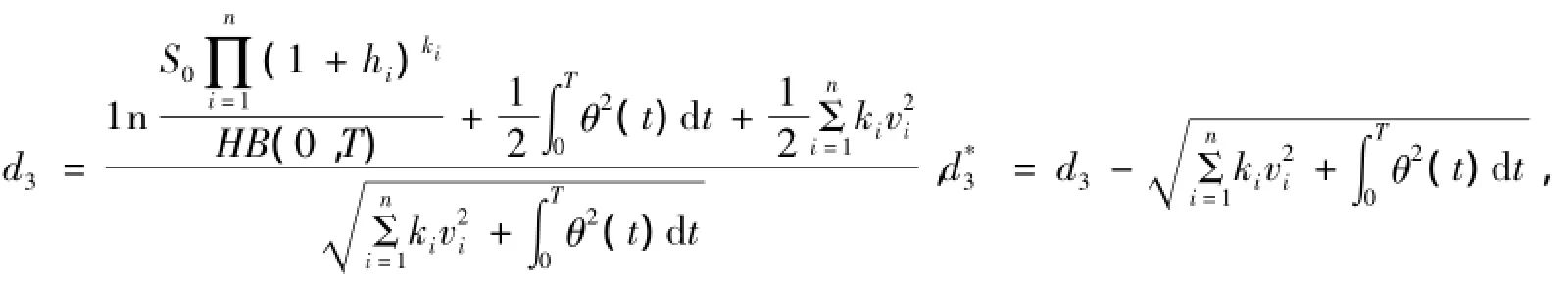
θ2(t)=σ2(t)+δ2(t，T)－2ρσ(t)δ(t，T)，且N(·)为标准正态分布的累积分布函数.

推论3股票价格过程S(t)和债券价格过程B(t，T)分别满足随机微分方程(1)、(2)，则到期日为T的抵付型权证在t时刻的定价公式为:

其中，

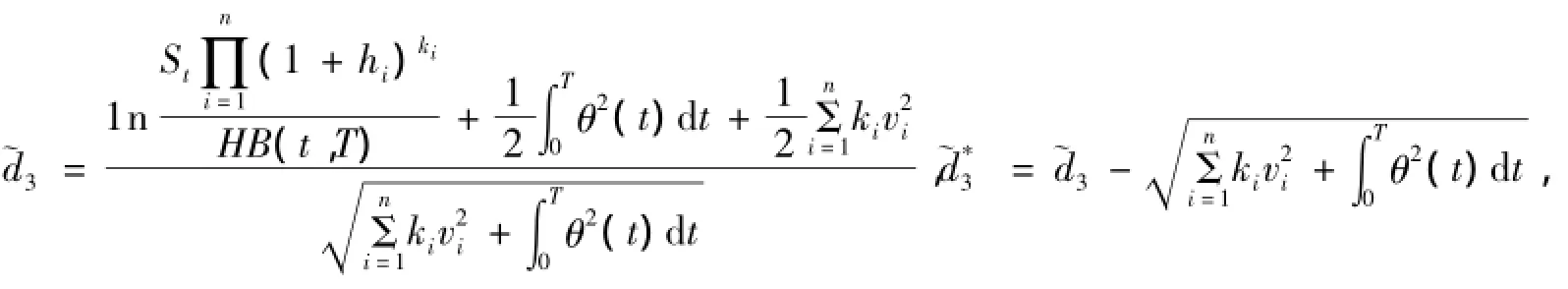
θ2(t)=σ2(t)+δ2(t，T)－2ρσ(t)δ(t，T)，且N(·)为标准正态分布的累积分布函数.

其中，文中所述的两种奇异期权中，当上限型权证的K2→∞，抵付型权证的K=H时，它们则为标准欧式看涨期权.

［1］Black F，Scholes M.The pricing of options and corporate liabilities［J］.Journal of Political Economy，1973(81):637－654.

［2］Merton R C.Option pricing when underlying stock return are discontinuous［J］.Journal of Economy，1976(3):125－144.

［3］宁丽娟，刘新平.股票价格服从跳－扩散过程的期权定价模型［J］.陕西师范大学学报(自然科学版)，2003(4):16－19.

［4］颜玲，王永茂，刘海涛，王怡菲，刘超，吴琳琳.有多个跳跃源的跳扩散模型的期权定价［J］.郑州大学学报(理学版)，2012(1): 33－36.

［5］赵建国，师恪.跳－扩散模型下的复合期权定价公式［J］.新疆大学学报(自然科学版)，2006(3):257－263，276.

［6］张波，商豪.应用随机过程［M］.北京:中国人民大学出版社，2001.

Pricing of Two Kinds of Exotic Options with Jump－Diffusion Model

ZHOU Shuang－jiao
(School of Applied Mathematics，Nanjing University of Finance and Economics，Nanjing，210046，China)

It is assumed that the jump process in stock price is a special kind of renewal process.The jump diffusion model with multiple sources of jumps is established under the stochastic interest rates.Based on equivalent martingale transformation measure，two exotic pricing formulas are deduced.

renewal process;stochastic interest rate;martingale method;exotic option

O211.6

A

1672－2590(2015)06－0018－06

2015－10－08

周双娇(1990－)，女，浙江青田人，南京财经大学应用数学学院硕士研究生.