基于PSF相关的星点定位算法*
2015-06-07郝云彩贾瑞明马晓蕾
郝云彩,贾瑞明,马晓蕾
(1.北京控制工程研究所,北京 100190; 2.北方工业大学,北京 100041)
基于PSF相关的星点定位算法*
郝云彩1,贾瑞明2,马晓蕾2
(1.北京控制工程研究所,北京 100190; 2.北方工业大学,北京 100041)
为提高非高斯分布星点定位的精度,提出了一种新的PSFC (point spread function correlation)星点定位算法,具有很好的抗噪性能和精度水平,易于工程实现.该算法利用互相关中的定义,通过确定系统所测定的PSF与星像灰度值之间的最大相似度来定位星点位置,PSF的测定是在作互相关计算之前全视场范围内可按照整像素和亚像素两种方式完成的.仿真实验结果表明:在带有噪声的星像图条件下,本文PSF相关法的定位精度最高可达到0.034像素,比质心法的精度提高1个数量级,比曲面拟合法的精度提高约20%.
点扩散函数;互相关法;亚像素;质心法
0 引 言
星敏感器是一种以恒星为参照物进行姿态测量的高精度敏感器;而星点提取中的质心定位精度是星敏感器的重要精度指标[1-2],将直接影响姿态角的测量精度,因此优化和提高星点提取中的质心定位精度具有十分重要的意义.对于星敏感器而言,恒星可以视为无限远的点光源,因此理论上星敏感器成像即为无限远点光源光学成像系统,其感光单元即为光学成像系统的焦平面[3],此时光学焦平面上星点能量分布可由点扩散函数表示出.在理想的光学系统下,恒星像点小于一个像元无法通过算法进行精确的定位,因此,通常利用散焦的方法使得像点弥散,扩大到数个像元,然后使用内插细分算法计算星点质心.目前所用的星点质心细分定位算法主要有质心法、高斯曲面拟合法和抛物面拟合法[4-5].
在这些算法中质心法主要有传统质心法和改进的质心法[6].传统质心法(TC,traditional centroid)计算简便,但受星点能量分布形状影响较大,当星点能量分布呈现几何非对称形状时误差较大,抗噪声能力变差,适用于星点能量分布呈对称状且没有背景噪声的情况;改进的质心法主要有灰度加权质心法(GWC,gray weighted centroid)、灰度平方加权质心法(GSWC,gray square weighted centroid)、距离加权质心法(WDC, weighted distance centroid),改进后的质心法抗噪能力不同程度均有所增加,但精度提高有限;高斯曲面拟合法(GCFM,gauss curve fitting methods)虽然具有较高的定位精度,但计算量大,易受到星点所占像元大小的影响,不适合对星图进行实时处理[7-9].
本文针对现有星点提取算法中乏少措施以改善噪声、S误差、星点能量分布不对称等因素带来的固有定位偏差,提出了一种利用PSF相关法(PSFC)来提高星敏感器星点质心定位精度,星敏感器全视场PSF分布模型可以实测加插值得到,使得PSFC法与以往方法相比,具有抗干扰能力强、精度高、处理速度快、便于星上实现等优点.通过计算机仿真与TC、GSWC和GCFM进行了实验对比与分析,验证了该算法的优越性.
本文的研究方法是采用理论分析和数学仿真的方法结合,对于工程实现途径也进行了概略分析.
1 传统星点图像的细分定位算法
1.1 质心法及改进算法
传统质心法是一种对目标图像灰度值的加权运算.权值随像元离目标像点灰度中心的距离增大而线性增长,且易受到目标像点分布形状和背景噪声的影响.当目标像点灰度分布关于峰值呈现非对称时,在使用质心法计算其像点质心坐标时误差变大[3].因此,为了提高传统质心法的定位精度对其进行了改进,主要有GSWC、WDC等.可表示为式(1):
(1)

采用灰度值作为加权函数的灰度平方加权质心法,突出了中心较大的灰度值像素点对中心位置的影响,使得星点光斑形状在即使不近似于高斯分布的情况下,该方法依然能较准确的提取质心,增强了算法的抗干扰能力.采用距离的倒数作为加权函数的距离质心法,由于距离星点光斑质心越远的像素对质心的判断影响越小,所以取距离的倒数作为加权函数可减少噪声对质心定位产生的干扰,提高星点质心定位精度.
1.2 高斯曲面拟合法
由于星点图像灰度近似于高斯分布,因此可以用高斯曲面对星点灰度分布进行拟合,求出其灰度最大值对应的坐标即可求得星点质心坐标,高斯曲面拟合函数可表示为
(2)
式中:A为高斯幅值;ρ为相关系数;(xc,yc)为特征像点的中心坐标;δx、δy分别为x和y方向的标准差;一般为简化计算,取ρ=0,δx=δy=0.则式(2)可简化为
(3)
对式(3)两边同时取对数,展开平方项整理,得
(4)
利用目标图像n个特征点的像素,通过基于约束的最小二乘法解方程(4),可以解出(xc,yc).
2 确定星像位置的PSF相关法(PSFC)
2.1 原理和概念
相关系数是用以反映变量之间相关关系密切程度的统计指标,相关系数是按积差方法计算,同样以两变量与各自平均值的离差为基础,通过两个离差相乘来反映两变量之间相关程度[12].其大小也可以反映两个不同的量之间的相似程度.数学公式为
(5)
式中,E是数学期望,cov表示协方差,δX和δY是标准差.
将这种相关系数的运算运用到星点细分定位中,也可以被用来计算星像的质心.对于星点图像g(x,y)与利用星点能量分布模型(PSF)所得到的模板f(x,y)进行相关操作,他们的互相关操作定义为
(6)
式中μf和μg分别为星点图像g(x,y)和PSF生成的模板f(x,y)的平均灰度值.当g(x,y)和f(x,y)的相似度越大时ρ值越大.因此,通过确定互相关函数取最大值时PSF峰值的偏移量即可确定目标星点的质心位置.
这种方法的优点是,利用PSF模板的精确性,消除星敏感器星像点由于噪声、S误差、不对称性造成的固有偏差,使得以往传统方法难以消除的定位误差借助于PSF相关算法得以很大程度的消除,这也是本文思想创新之处.
2.2 PSFC法的仿真流程
本文中根据相关法的基本原理提出了两种PSF相关算法.一种是基于PSF的亚像素相关算法,一种是基于PSF的整像素相关算法.亚像素相关法是把得到的星敏感器的星点灰度图人为进行亚像素细分,细分后所有的网点总数量与PSF测量采样的网格点数量相同,细分网点处的灰度采用所测PSF插值得到,这样的星点图同样携带了S误差和噪声产生的灰度分布.PSF测量师按照亚像素分辨率进行,它与细分后的星点图分布相关运算找最大相关系数,PSF峰值偏移量即是星点偏移量.整像素相关法是相关运算采用星敏感器直接获取的星点图,不需要把它细分,而测量的PSF需要用高于星敏感器分辨率的探测器采样,然后按照原始像素尺寸积分得到PSF的某偏移量分布,以偏移量迭代的PSF与星敏感器原始星图相关求相关系数,最大值处的偏移量即是所求.
基于PSF的亚像素相关算法步骤如下:
(1)对星点图像进行预处理:提取星点图像的目标区域g(xi,yi),并得到目标区域的大小;
(2)对星点图像的目标区域g(xi,yi)进行高分辨率采样,得到亚像素序列g′(xi,yi);
(3)对星点灰度分布满足的PSF进行积分,积分间隔与式(2)中高分辨率采样的间隔相同,得到与目标区域大小相同的积分序列;
(4)将(2)中所得到的亚像素序列g′(xi,yi)与(3)中所得到的积分序列f(xi,yi)进行相关操作,求出相关函数取得最大值时PSF峰值的偏移量Δd,从而确定星点质心位置.
该方法的流程图如图1所示.

图1 PSF亚像素相关算法流程图Fig.1 PSF sub pixel correlation algorithm flow chart
基于PSF的整像素相关算法步骤如下:
(1)对星点图像进行预处理:提取星点图像的目标区域g(xi,yi),并得到目标区域的大小.
(2)对星点灰度分布满足的PSF以像元为单位进行积分,得到与目标区域大小相同的积分序列.
(3)以间隔为0.01平移(2)中所得到的积分序列的起始点,得到一系列PSF积分序列f(xi,yi).
(4)将(1)中所得到的目标区域与(3)中所得到的一系列PSF积分序列进行相关,求相关系数最大值所对应的PSF积分序列.
(5)通过(4)中所求得的PSF积分序列所对应的最大值即可确定星点质心坐标.
该方法的流程图如图2所示.
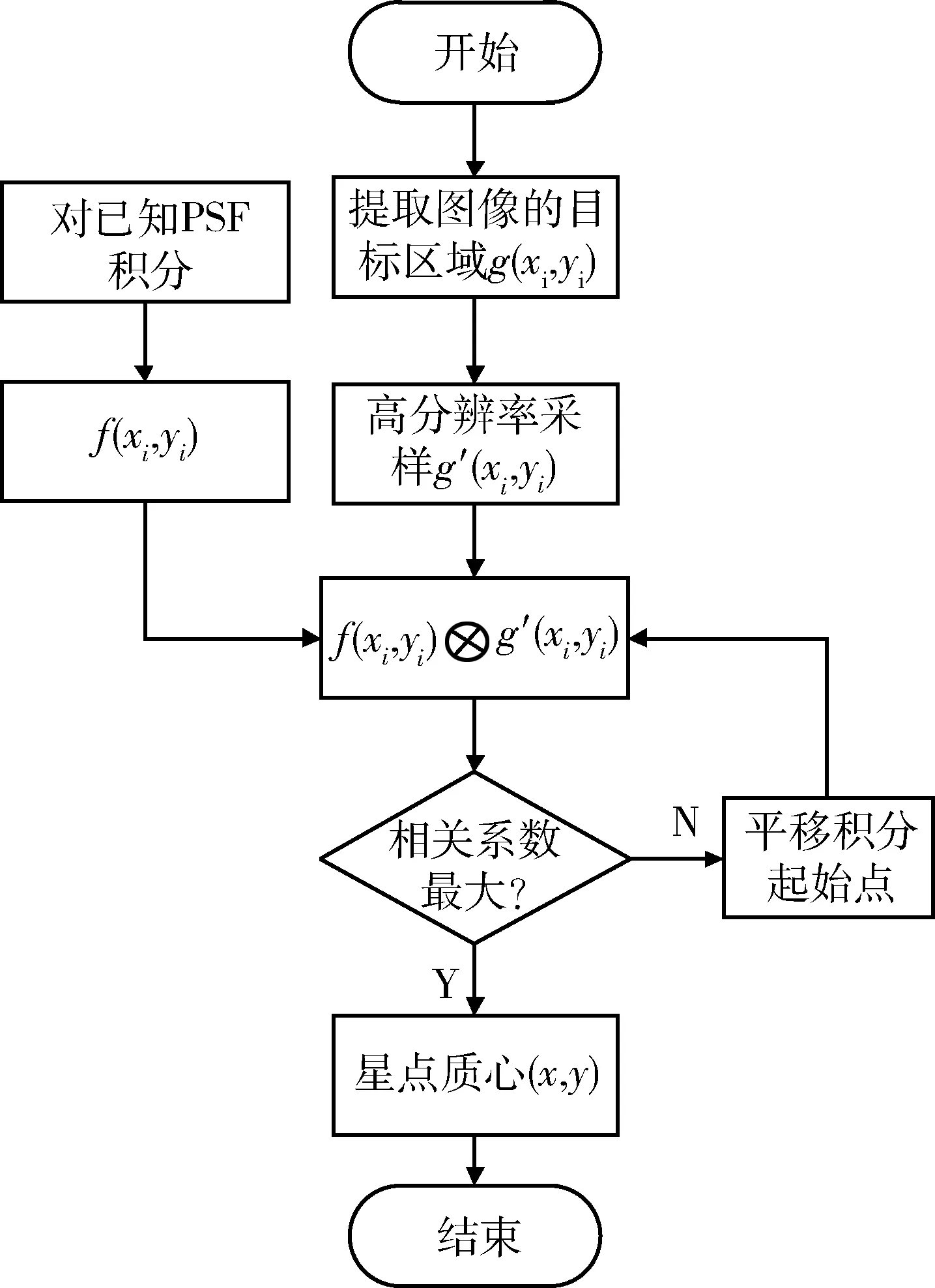
图2 PSF整像素相关算法流程图Fig.2 PSF full pixel correlation algorithm flow chart
3 实验与结果分析
3.1 生成仿真图像
上文对各种算法进行了初步的理论分析,为了对所提算法精度进行验证,通过利用灰度分布近似于高斯型的PSF模拟生成星图,进行实验验证.模拟生成图像大小为64×64、背景灰度为0的单星星图.模拟生成星点图像的PSF为
(7)
其中星图灰度幅值A=160,选择不同的弥散半径δ使得模拟星点图像在某一方向所占大小范围为[3,10].
在本文中选择星点质心坐标在x方向的一个像素内(xc=31.5~32.5)变动,在y方向没有移动;xc以0.01为间隔依次增加,得到101幅模拟的理想星图. 图3中,(a)为δ=0.85时所生成的无噪声仿真星图,(b)为δ=0.85时生成的含有高斯噪声(均值为0,方差为0.001)的仿真星图.

图3 仿真星图Fig.3 The simulation image
3.2 无噪声星点图像实验与分析
分别利用本文中所提到的4种算法提取理想仿真星图的质心坐标,并求出与实际值的偏差Δx,得到误差曲线图;并计算各个算法的算术平均误差进行比较.图4(a)和图4(b)为δ=0.85时使用各算法得到的误差曲线图.
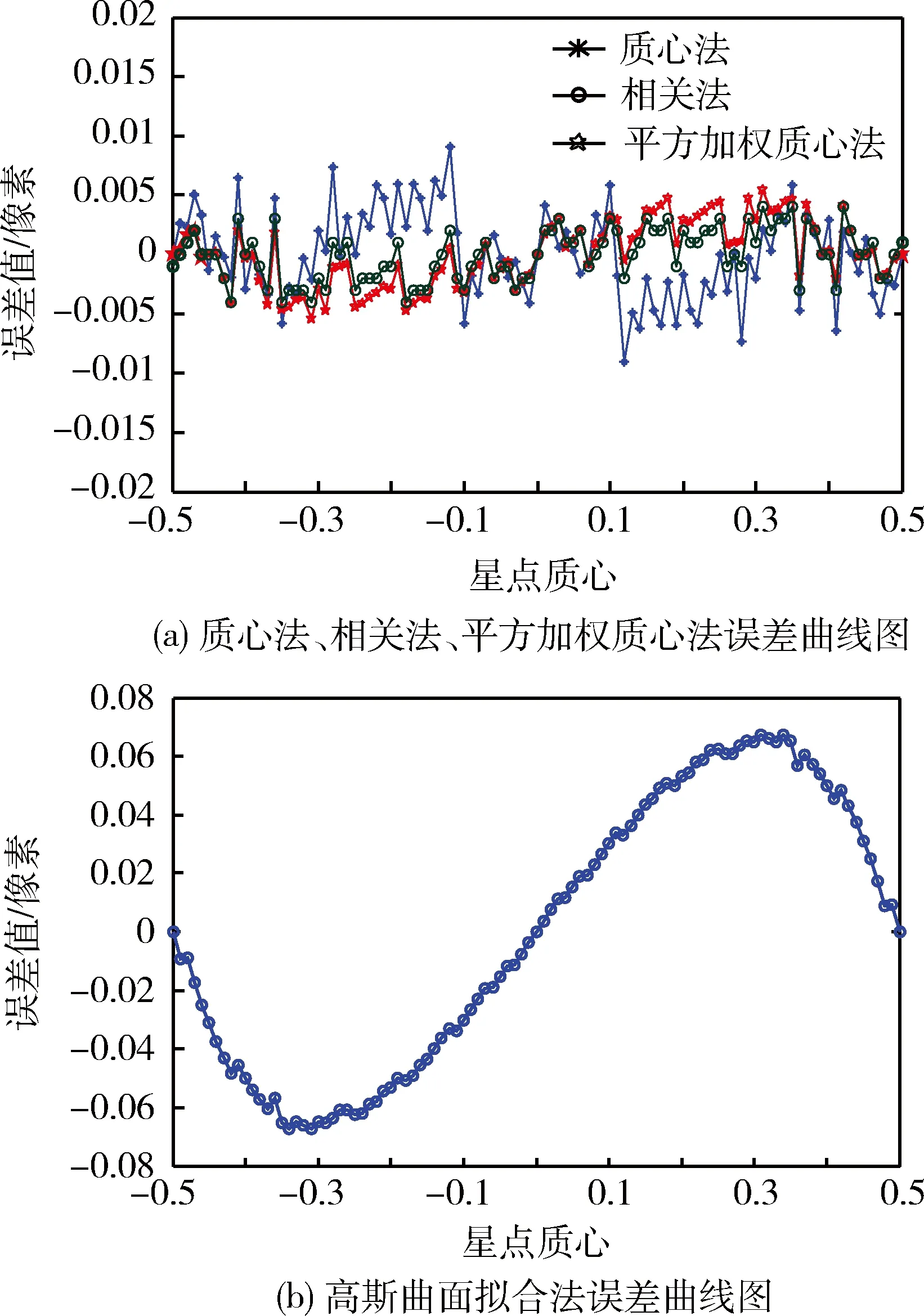
图4 误差曲线图Fig.4 The error curves
经试验数据统计可知,当δ取不同值时,误差曲线的形状不同;当δ较小时即星点所占像元较少时,星点质心提取误差与真实误差近似成S形曲线,随着δ的增大星点质心提取误差与真实误差呈现锯齿形.其中,S曲线误差是质心定位系统误差的重要组成部分,它表现为当像点能量中心在像素内均匀移动时,质心位置与像点能量中心之间的以像素为周期类似正弦规律变化的误差.
通过计算可得出传统质心法、平方加权质心法、高斯曲面拟合法、PSF整像素相关法和PSF亚像素相关法的算术平均误差值分别为0.002 9、0.002 4、0.041、0.001 7、0.002 8.
图5为表1所对应的算术平均误差曲线图.
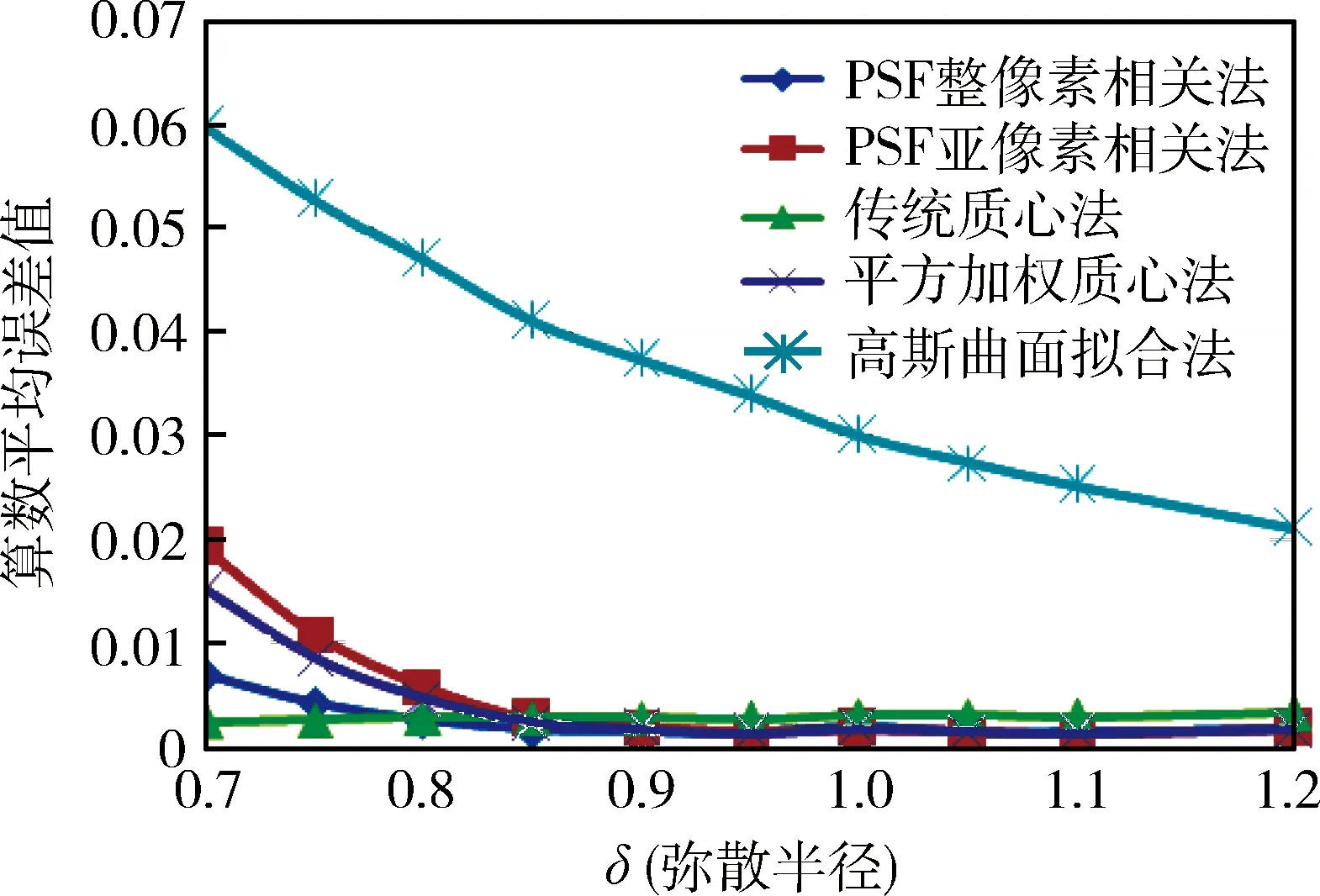
图5 无噪声时各算法的算术平均误差曲线Fig.5 The error curves of arithmetic average for each algorithm without noise
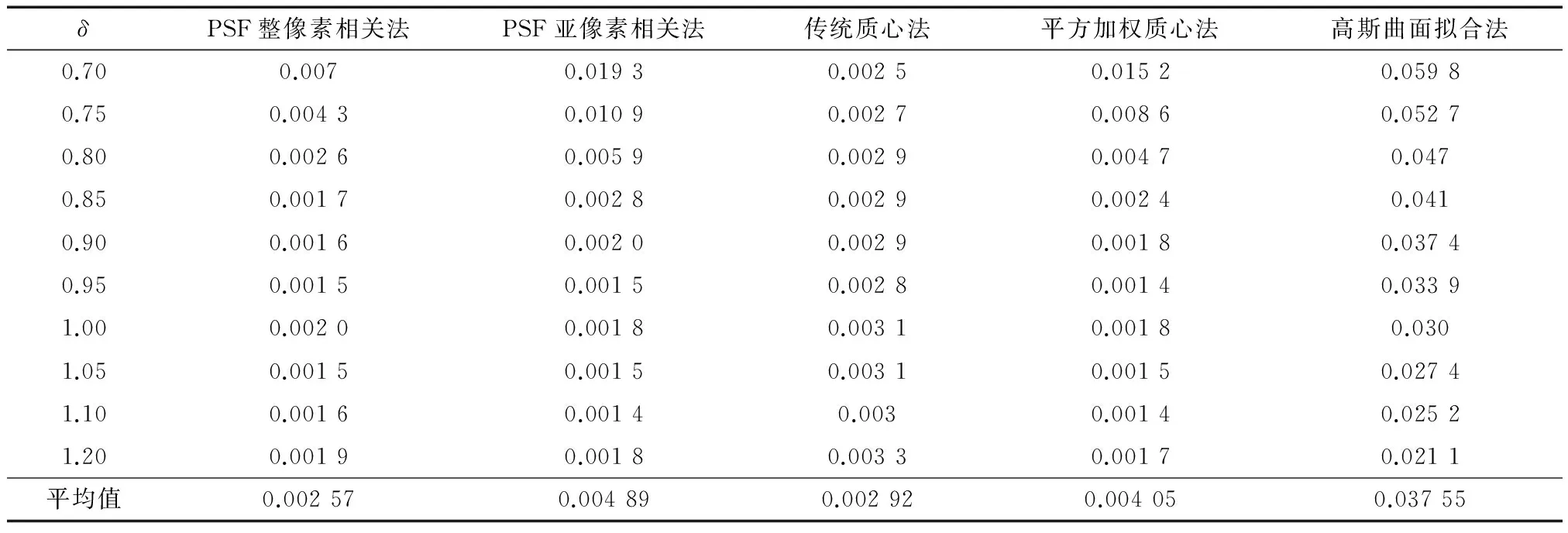
δPSF整像素相关法PSF亚像素相关法传统质心法平方加权质心法高斯曲面拟合法0.700.0070.01930.00250.01520.05980.750.00430.01090.00270.00860.05270.800.00260.00590.00290.00470.0470.850.00170.00280.00290.00240.0410.900.00160.00200.00290.00180.03740.950.00150.00150.00280.00140.03391.000.00200.00180.00310.00180.0301.050.00150.00150.00310.00150.02741.100.00160.00140.0030.00140.02521.200.00190.00180.00330.00170.0211平均值0.002570.004890.002920.004050.03755
从图5和表1可以看出,在不含噪声的仿真星图下,随着δ的增大(像元所占数目增多)各个算法的误差均呈减小趋势;其中,高斯曲面拟合法较其他几种算法误差最大;在δ取值较小时传统质心法比平方加权质心法和相关法误差小,随着δ的增大,平方加权质心法和相关法误差减小效果均好于传统质心法,但相关法比较稳定,在δ<0.9时相关法误差小于平方加权质心法,随着δ的增加两者相差不大.
3.3 含噪声星点图像实验分析
在真实拍摄中所得到的星图是含有噪声的,为了使仿真结果更接近实际情况,对模拟生成的星图添加了均值为0,标准方差为0.001的高斯噪声.图6(a) 和图6(b)为δ=0.85时使用各算法计算含有噪声的星图得到的误差曲线图.

图6 误差曲线Fig.6 Error curves
同样,通过计算可得出在含有噪声的星图中传统质心法、平方加权质心法、高斯曲面拟合法、PSF整像素相关法和PSF亚像素相关法的算术平均误差值分别为1.038 8、0.501 0、0.062 5、0.039 1.
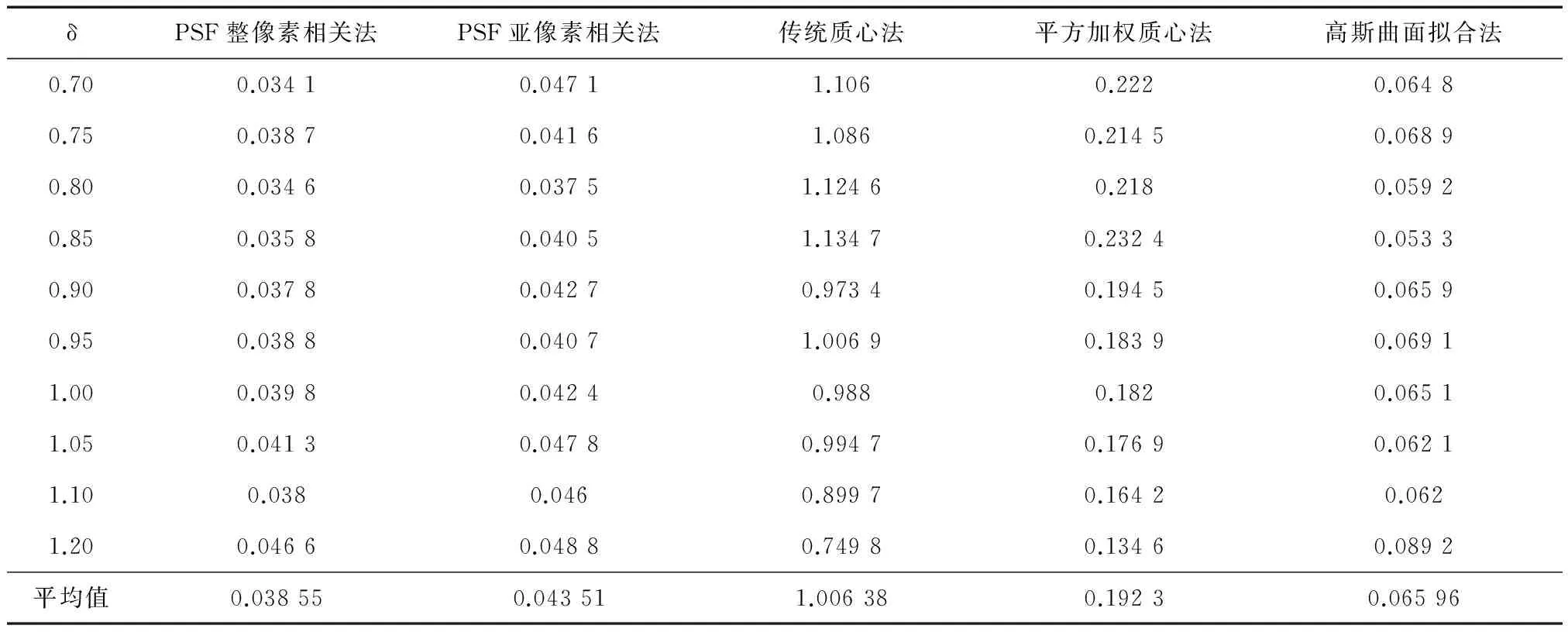
表2 含噪声星图在不同δ取值时各算法的算术平均误差值
图7为表2所对应的算术平均误差曲线图.
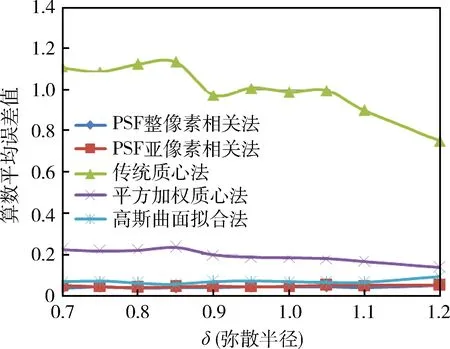
图7 各算法的算术平均误差曲线(含噪声)Fig.7 The error curves of arithmetic average for each algorithm (with noise)
表3为本文中各算法在无噪声星图和有噪声星图下的算术平均误差值.

表3 各个算法的算术平均误差值
从表3和图7可以看出,在含有噪声的星图下,各种算法的误差均比理想星图的误差要大;其中,传统质心法和平方加权质心法在含有噪声的星图中误差明显变大;相关法和高斯曲面拟合法误差比质心法要好,且相关法误差明显比高斯曲面拟合法要好.
3.4 PSFC星点定位法的工程实现途径探讨
如上文所述,PSF是采用数学仿真的方法得到的,在实际星敏感器应用中,应当采用PSF测试设备,对于全视场范围PSF进行网格测量,并分区进行多项式插值计算网格点外的PSF.我们对此也进行了相应的实验工作,限于篇幅不在此介绍,将另文发表.
地面实验室测量的PSF可以作为星敏感器的标定文件存储起来,每幅图像获取的星点像灰度图首先采用传统质心法计算出其位置坐标,再在此处插值出来PSF,然后按照本文提供的PSFC法进行星点质心确定,必会提高星点定位精度.
4 结 论
目前通用的质心法中,由于传统质心法和平方加权质心法受到星点灰度分布两侧的峰值及几何形状的影响较大,且实际所拍摄到的星图都是含有噪声的,因此这两种方法在星敏感器系统精度要求较高的情况下计算误差较大,而高斯曲面拟合法易受到星点像元范围的影响,应用范围有限.针对以上算法的缺点,本文提出了基于PSF相关法来提高星点图像质心精度,介绍了基于PSF的亚像素相关算法和基于PSF的整像素相关算法两种方法.在拥有地面PSF模板测试数据的条件下,亚像素PSF相关法可以在很大程度上解决系统噪声、S误差、星点不对称等传统方法望之兴叹的问题.
通过仿真实验表明,在不含噪声的星图中基于PSF相关法的误差与传统质心法误差相差不大,但在含有噪声的星图中基于PSF相关法的定位精度数量级可达到-2,误差明显小于传统质心法、平方加权质心法的0~-1个数量级,且高于高斯曲面拟合法1.2~2倍,定位精度更加稳定.因此,基于PSF相关法的适用范围更加广泛,抗噪性能更好,在实际的星图质心提取中定位精度高于质心法、高斯曲面拟合法.
[1] 贾辉. 高精度星敏感器星点提取与星图识别研究[D].长沙: 国防科技大学研究生院,2010. JIA H. Study on star extracting and star map recognition for a high accuracy star sensor[D]. Changsha: National University of Defense Technology, 2010.
[2] LIEBE C C. Accuracy performance of star trackers-a tutorial[J]. IEEE Transtion on Aerospace and Electronic Systems, 2002, 38(2): 587-599.
[3] 张新宇,郝云彩.星敏感器星点能量分布数学模型及其对精度的影响分析[J].空间控制技术与应用,2013,39(3):14-23. ZHANG X Y, HAO Y C. Analysis of the star image energy distribution mathematical model and its effect on the accuracy for a star tracker[J]. Aerospace Control and Application, 2013, 39(3): 14-23.
[4] 魏新国,张广军,江洁.星敏感器中星图图像的星体细分定位方法研究[J].北京航天航空大学学报,2003,29(9):812-815. WEI X G, ZHANG G J, JIANG J. Subdivided locating method of star image for star sensor[J]. Beijing University of Aeronautics and Astronautics, 2003, 29(9): 812-815.
[5] RUFINO G, ACCARDO D. Enhancement of the centroiding algorithm for star tracker measure refinement[J]. Acta Astronautica, 2003, 53: 135-147.
[6] 李玉峰,郝志航.星点图像超精度亚像元细分定位算法的研究[J].光学技术,2005,31(5):666-671. LI Y F, HAO Z H. Research of hyper accuracy subpixel subdivision location algorithm for star image[J]. Optical Technique, 2005, 31(5): 666-671.
[7] 邓江生,樊利恒,古立莉.星图像的亚像元细分定位方法研究[J].电子设计工程,2012,20(22):186-189. DENG J S, FAN L H, GU L L. Research on method for sub-pixel location of star image[J]. Electronic Design Engineering, 2012, 20(22): 186-189.
[8] 李光蕊.基于高斯分布的星点图像亚像元定位算法研究[J].光学技术,2011,37(1):57-61.
[9] LI G X. Research of sub-pixel location algorithm for star image based on Gaussian distribution[J]. Optical Technique, 2011, 37(1): 57-61.
[10] WANG H Y, ZHOU W R, CHENG X, et al. Image smearing modeling and verification for strapdown Star sensor[J]. Chinese Journal of Aeronautics, 2012, 25(1): 115-123.
[11] 孙瑾秋,周军,张臻,等.基于能量累加的空间目标星像质心定位[J].光学精密工程,2011,19(12):3043-3048. SUN J Q, ZHOU J, ZHANG Z, et al. Centroid location for space targets based on energy accumulation[J]. Optics and Precision Engineering, 2011, 19(12): 3043-3048.
[12] LI H, SONG H, RAO C, et al. Accuracy analysis of centroid calculated by a modified center detection algorithm for Shack-Hartmann wavefront sensor[J]. Optics Communications, 2008, 281(4): 750-755.
[13] 李春艳,谢华,李怀锋,等.高精度星敏感器星点光斑质心算法[J].光电工程,2006,33(2):41-44. LI C Y, XIE H, LI H F, et al. Centroiding algorithm for high-accuracy star tracker[J]. Opto-electronic Engineering, 2006, 33(2): 41-44.
Star Locating Algorithm Based on PSF Correlation
HAO Yuncai1, JIA Ruimin2, MA Xiaolei2
(1.Beijing Institute of Control Engineering, Beijing 100190, China;2.North China University of Technology, Beijing 100081, China)
In order to improve the star locating accuracy with non Gauss energy distribution for a star tracker, a new locating algorithm based on PSFC (point spread function correlation) was proposed. The new method has good anti noise performance, high accuracy and engineering realization. The PSFC locating algorithm is realized by using cross correlation definition and determining the maximum similarity of the measured star PSF and the star gray images of the star tracker. The measured star PSF are prepared before cross correlation computation by all the FOV sub-pixel measurements. The simulation results show that the accuracy of PSF correlation method considering high noise background can reach 0.034 pixels, and is higher than the traditional centroid method of 1 orders of magnitude , and is higher than the Gauss surface quasi legal of about 20%.
point spread function correlation ; cross correlation; sub pixel; centroid method.
*国家自然科学基金资助项目(61174004).
2015-11-03
V448
A
1674-1579(2015)06-0001-07
10.3969/j.issn.1674-1579.2015.06.001
郝云彩(1966—),男,研究员,研究方向为空间目标探测与光学敏感器,空间光学和光学自主导航技术;贾瑞明(1978—),男,助理研究员,研究方向为空间目标跟踪与识别,模式识别与图像处理;马晓蕾(1989—),女,硕士研究生,主要研究方向为图像处理与模式识别.
