基于迭代学习算法的控制力矩陀螺框架扰动抑制策略研究*

来 林，周大宁，武登云

(北京控制工程研究所，北京 100190)



基于迭代学习算法的控制力矩陀螺框架扰动抑制策略研究*

来 林，周大宁，武登云

(北京控制工程研究所，北京 100190)

卫星的快速机动以及高精度姿态控制，越来越依赖高精度的控制力矩陀螺(CMG)力矩输出，这就需要CMG低速框架能够有效抑制扰动力矩，降低转速波动.对由高速转子动不平衡引起的扰动力矩进行了分析和建模.为了抑制该扰动力矩对低速框架转速稳定性的影响，在传统的低速框架PID双环控制系统上嵌入了迭代学习的控制算法.通过仿真实验验证该控制方法能够有效抑制扰振力矩，大幅度的提高CMG的输出力矩精度.

CMG；迭代学习；扰动抑制

0 引 言

控制力矩陀螺陀螺(CMG ，control moment gyroscope)是一种重要的空间执行机构，它由转子组件和框架组件两部分组成.高速转子以恒定的角速度旋转，提供了一个恒定的角动量，框架组件驱动转子组件围绕垂直于角动量矢量方向的框架轴旋转，改变角动量矢量方向，以此来实现CMG与航天器之间的角动量交换，同时输出陀螺力矩，实现航天器的快速机动和姿态稳定[1-2].

近些年来，随着对卫星在姿态机动时间和稳定性的要求不断提高，对承担星体机动和姿态稳定的CMG，在其输出力矩精度和稳定度等方面也提出了更加严苛的要求.CMG的输出力矩表达式为

Toutput=H×ω

(1)

由于高速转子始终工作在恒定转速下，且受到的阻力矩较为恒定，故其转速精度较高，即能提供高精度的角动量H输出.因此决定CMG输出力矩精度和稳定度的关键，就是低速框架的转速ω的控制性能[3].

单框架控制力矩陀螺 (SGCMG， single gimbal CMG)低速框架的驱动一般使用永磁同步电机[4].在结合了矢量控制后，永磁同步电机具有在低速转动状态下输出力矩精度高，控制性能好的特点.为了进一步提高永磁同步电机的输出力矩精度，即抑制电机的输出力矩波动，许多种不同的控制方案被提出.其中文献[5-7]针对永磁同步电机本身的控制提出了相应的控制策略，文献[8-9]针对电机在CMG低速框架驱动上的应用提出了控制方案.这些方案主要抑制了电机由于齿槽效应、磁场谐波以及电流量化误差等因素产生的扰动力矩，使输出力矩波动更小.而对于CMG，由于高速转子的动不平衡，会产生一个周期性变化的扰动力矩，该力矩直接作用在框架上，是CMG低速框架扰振的一个重要来源.为实现对输出力矩的高精度控制，就必须消除动不平衡产生的扰动力矩.传统的双环PID控制器，在抑制这种频率较高且幅值较大的扰动上，不能够达到理想的效果.

迭代学习控制策略的主要思想是，针对在有限区间上周期性运动的动态系统，利用上一周期迭代的误差量来修正当前的控制给定，直至系统的输出能够完全跟踪期望轨迹[6-7].在本文中，迭代学习控制策略被引入到双环PID控制系统中.在不改变原有控制系统的架构下，通过内嵌迭代学习模块，达到抑制周期性波动的转子动不平衡力矩的目的.

1 CMG框架扰动模型

对于框架电机为永磁同步电机的CMG，基于两相旋转坐标系(d-q坐标系)的电机输出电磁转矩表达式为

Te=Pnψfiq

(2)

式中，ψf为永磁体磁链；Pn为电机极对数.一般认为ψf为常量，故有永磁同步电机输出电磁转矩Te与q轴电流iq成正比.理想的电机伺服系统，其动力学方程可以表示为

(3)

式中，J为负载的转动惯量，ωm为电机轴的机械转速，Tf为阻力矩.而对于SGCMG，由高速转子动不平衡所产生的力矩，是使框架电机产生扰动的重要来源，也是影响转速控制精度和稳定度，进而影响CMG输出力矩精度和稳定度的重要干扰力矩.

对于作用在低速框架上的，由转子动不平衡所引起的扰动力矩，可以表示为[10]

Timbalance=(IwIx+IwIy)n2[Γcos(nt)+Φcos(nt)]

(4)

式中，n为转子转速，IwIx与IwIy分别为转子相对于其质心的惯量,Γ，Φ为转子动不平衡量.由上式可知，动不平衡引起的干扰力矩，其幅值与转子转速的平方成正比，频率与转子频率相同.故SGCMG框架轴向动力学方程可以由式(3)改写为

(5)

式(4)中给出了动不平衡扰动力矩的表达式，而在对CMG进行振动测试时，发现实际作用在低速框架上的扰动力矩频率不仅仅只有基频，即高速转子转速频率，还有其相应的倍频分量.图1为CMG转子为标称转速时的扰动实测值，几条谱线分别表示了作用在框架上的扰动频率和幅值，其中左边第一条谱线为实测高速转子的基频谱线，向高频方向看，可以清楚的看到3，5，7倍频的扰动谱线.

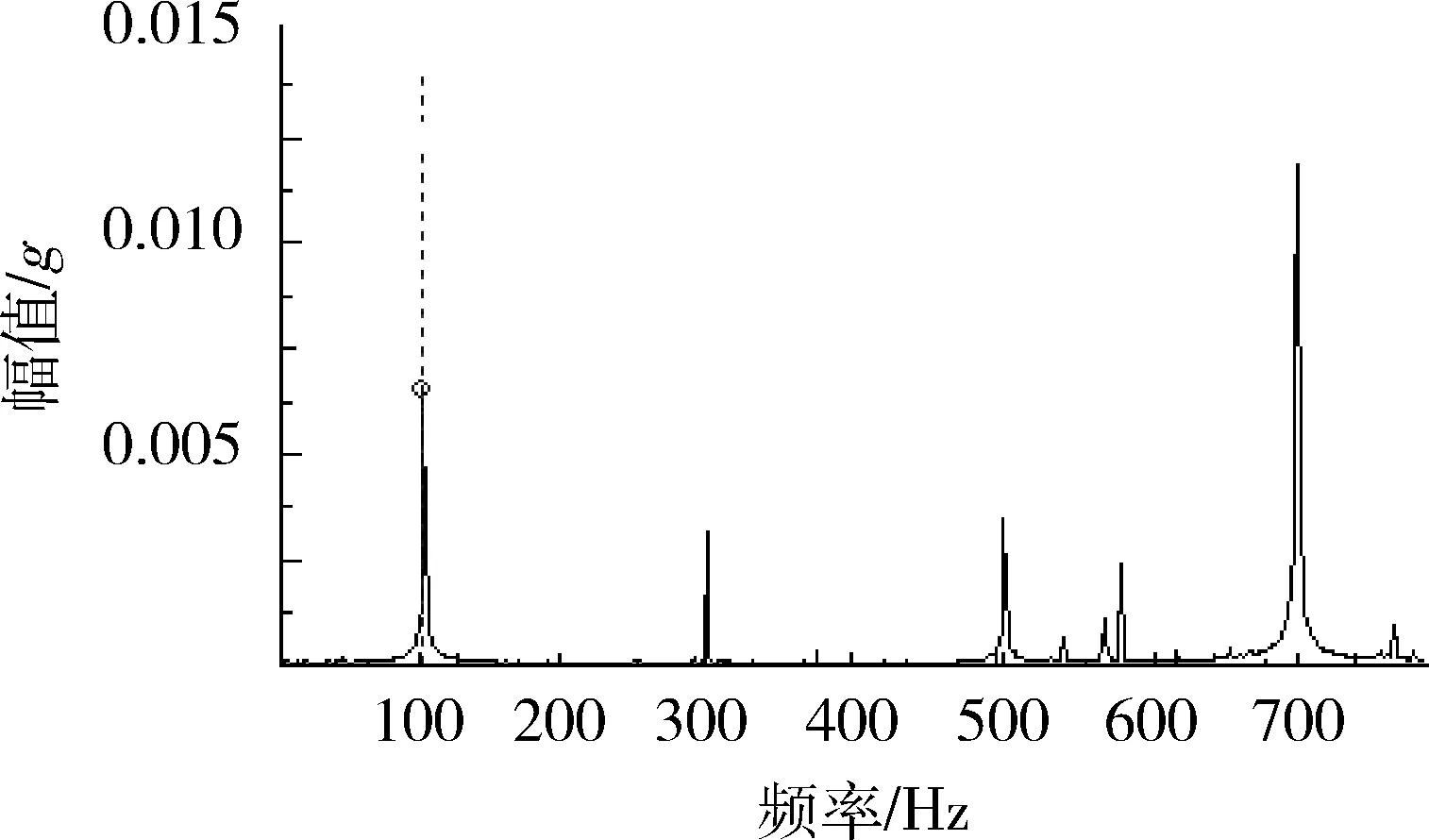
图1 高速转子扰动作用在框架上的频率谱线Fig.1 Frequency analysis of wheel disturbance acting on CMG gimbal

根据图1中的动不平衡扰动实测值，并结合由动不平衡引起的扰动力矩的基频表达式(4)，可以较为真实地模拟出由基频和其倍频组成的此干扰力矩在时域上的作用效果.而对此模型采取的控制策略，其仿真结果也会更接近实际控制效果.

2 迭代学习控制算法

CMG低速框架的控制，一般采用传统的基于双环PID的控制系统.内环为电流环，保证力矩的快速响应；外环为速度环，保证CMG的低速框架能够按照给定转速指令旋转，以输出需要的力矩.控制系统结构如图2所示.

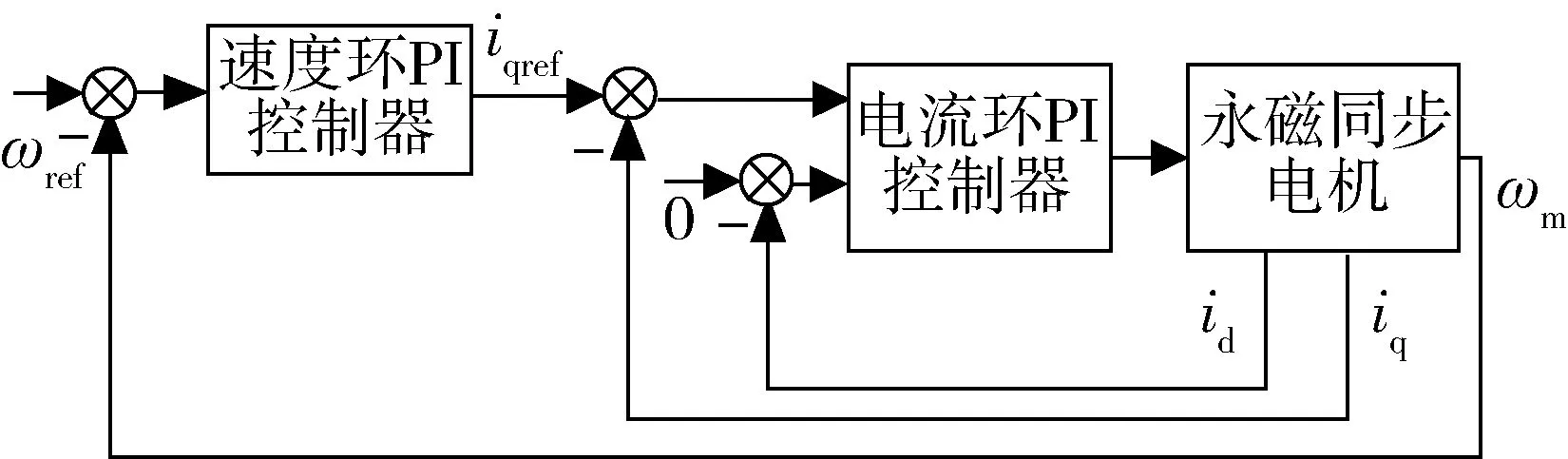
图2 传统的双环PID控制器Fig.2 Gimbal Servo System with PID Controller

双环PID控制器，对于变化缓慢的扰动力矩有较好的抑制效果，但对于频率高、且幅值较大的扰动力矩，如转子动不平衡扰动力矩，经双环PID控制器调节后，低速框架转速仍然会出现一个幅值较大的波动，影响了CMG输出力矩的精度与稳定度.

从上一节CMG框架扰动模型可知，转子动不平衡扰动力矩是以高速转子转速为基频，包含其3、5、7倍频的频率成分，其突出特点就是周期性.对于这些已知频率的周期性力矩扰动，迭代学习算法(ILC， iterative learning control)，是一种非常有效的抑制扰动的控制方法.迭代学习控制模块可以作为一个内嵌模块，放在传统双环控制器的两个比例积分模块中间，用以替代原有的产生电流给定值的模块，如图3所示.

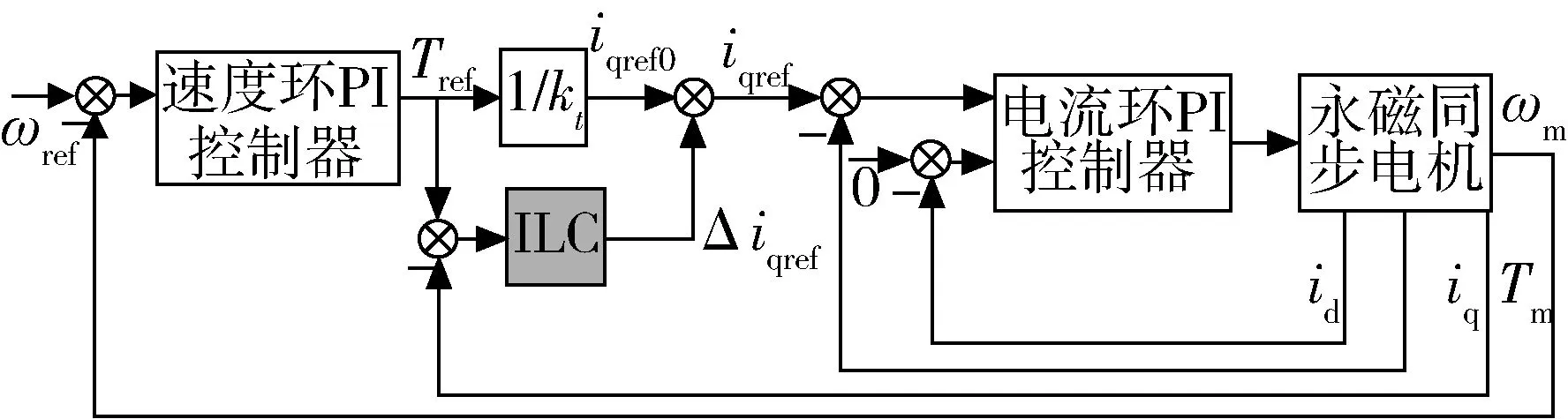
图3 加入迭代学习控制模块的闭环控制系统Fig.3 A closed-loop control system with iterative learning control module

图3中，kt为d-q坐标系下的电机力矩系数.控制器学习并且产生出一个补偿的电流给定值，叠加在原有的电流给定值之上，使得输出的转矩能够抵消掉周期性扰动的转子动不平衡力矩.这种控制方法的一个优势是它不改变原有双环控制器的结构，只是系统内叠加了自学习的模块.在不适用迭代学习控制的情况下，如暂态过程，也可以很方便的将该模块切掉，系统仍然可以保持在双环PID控制器下的控制效果.迭代学习控制算法的表达式为

Δiqref,i+1(θ)=(1-α)Δiqref,i(θ)+

kclei(θ)+kolei+1(θ)

(6)

其中

ei+1(θ)=Tref(θ)-Tm,i+1(θ)

(7)

式中，θ为高速转子的机械角度.各个值是以θ为变量的，而不是时间t，因为从式(4)动不平衡扰动力矩的表达式中可以看出，其波动周期为θ的周期.从式(6)中可以看出，在每个周期里，新的电流补偿值Δiqref,i+1(θ)，是通过上一周期的电流补偿值Δiqref,i(θ)和误差值ei(θ)计算得到的.迭代学习控制相当于一个在两个迭代周期之间的开环前馈控制，因此它对很小的波动都表现的极为敏感.因此本周期的ei+1(θ)也被引入到表达式中，以增加其稳定性.α∈[0,1]为遗忘因子，它保证了在更好地学习和系统鲁棒性之间的一种平衡[6].迭代学习控制模块的结构如图4所示.

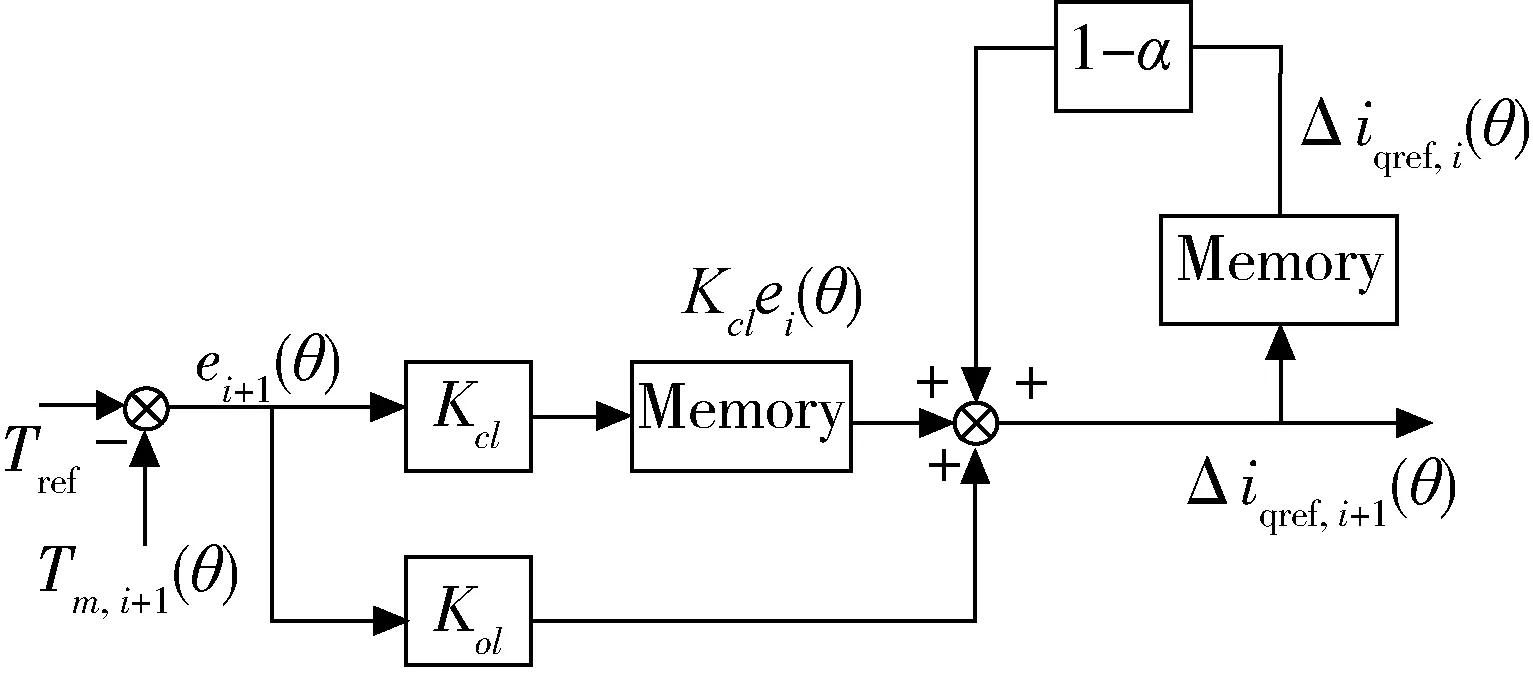
图4 迭代学习控制模块Fig.4 Iterative learning control module

3 仿真实验

为了对迭代学习控制算法的控制效果进行验证，本研究建立了低速框架驱动控制系统数值仿真模型.框架电机的参数如表1所示,CMG参数如表2所示.

表1 框架电机参数

在仿真实验过程中，选取迭代学习控制器控制参数α=0.05，kol=0.01，kcl=0.01.设定低速框架的转速为5(°)/s，当框架转速稳定后，图5显示了采用传统双环PID控制器得到的CMG低速框架转速曲线.可以看出转速在给定值5(°)/s的附近，有±1(°)/s的波动.

表2 CMG模型参数

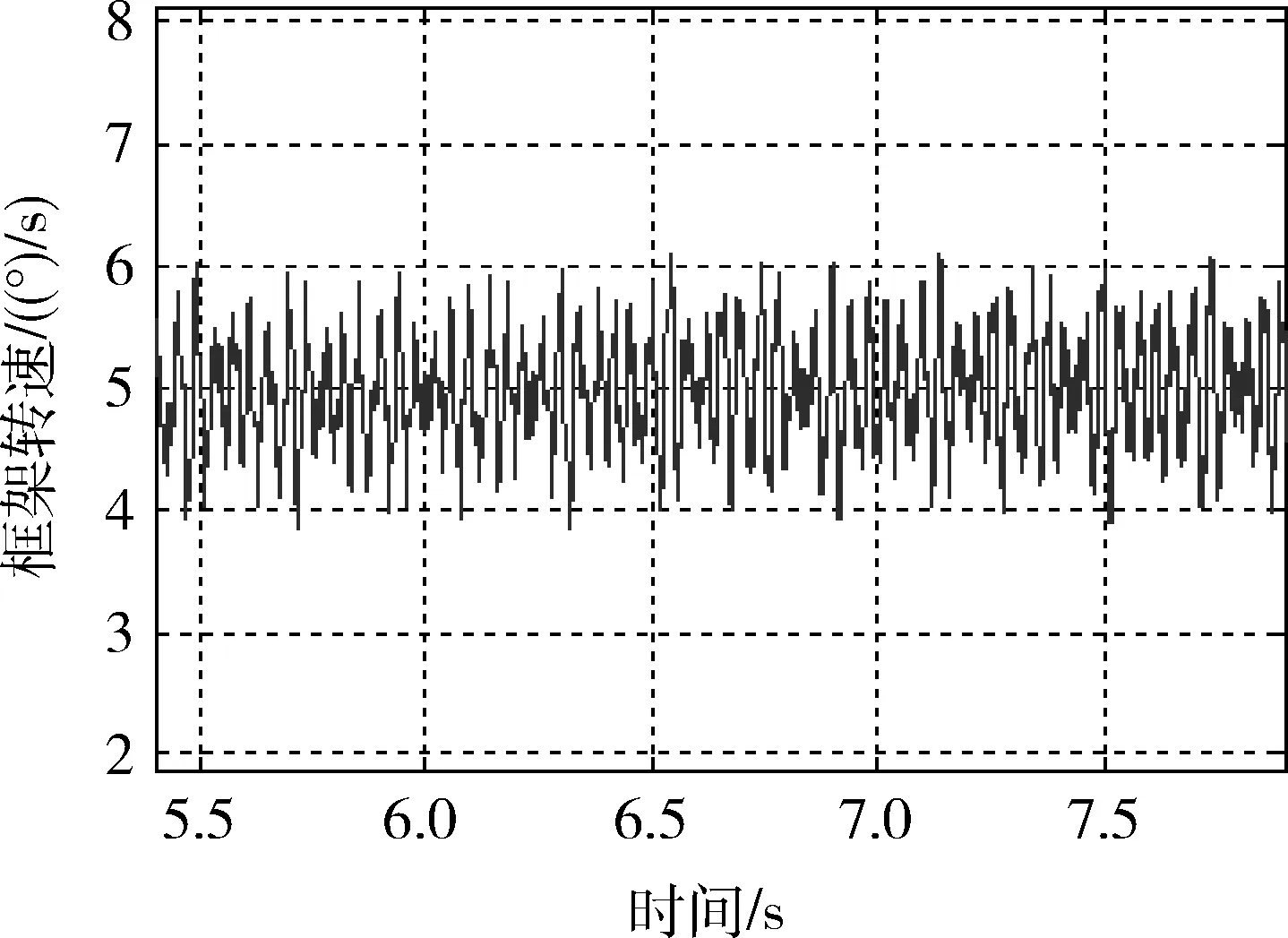
图5 双环PID控制下的低速框架转速曲线Fig.5 Gimbal speed with PID controller

通过在传统双环PID控制器中加入迭代学习内嵌模块，图6为得到的框架转速曲线.可以看出，输出框架转速的波动明显降低，与之相对应的转速精度，稳定度值将有大幅度提高.采用kSRF=Spp/Save，来比较两种控制方法对框架电机转速的控制效果.采用双环PID控制器的kSRF=40%.而加入了迭代学习模块，kSRF=14%.对于CMG而言，大幅度的降低框架的转速波动，就会大大提高输出力矩的精度，从而进一步提高整星的机动性能以及搭载的光学成像设备的成像效果.

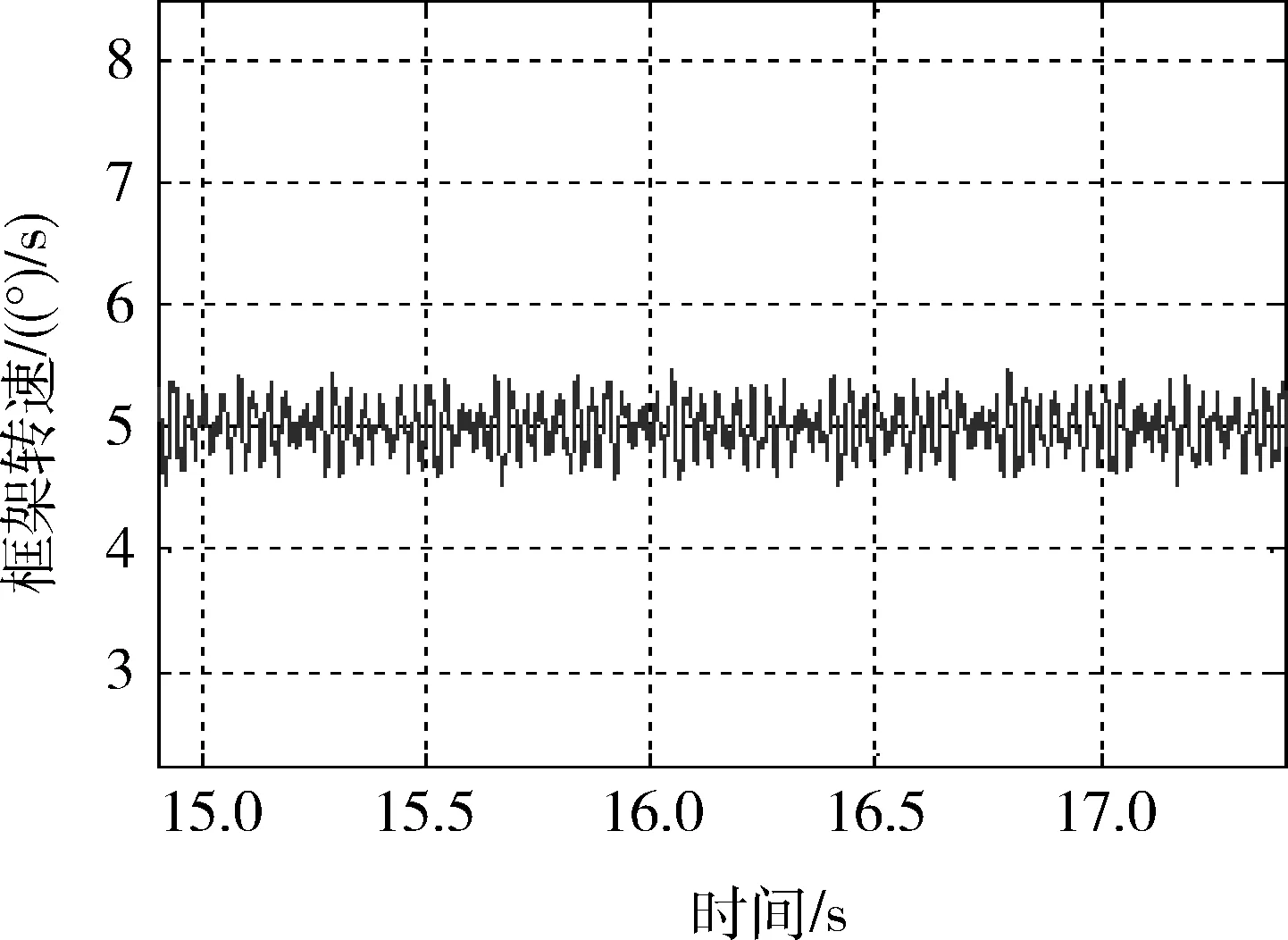
图6 加入迭代学习模块的低速框架转速曲线Fig.6 Gimbal speed with iterative learning control strategy

图7对加入迭代学习模块前后q轴电流的频谱进行了分析，可以明显的看出，在加入迭代学习控制算法后，q轴电流的频谱里100 Hz，300 Hz，500 Hz，700 Hz的频率成分幅值有明显的增加，这些频率成分与动不平衡扰振力矩的基频和倍频成分是相一致的.加入迭代学习模块后，该模块会在原有的电流给定值基础上叠加一个Δiqref，通过这个叠加量来抵消周期性扰动力矩对低速框架的影响，从而达到降低框架转速波动量的效果.

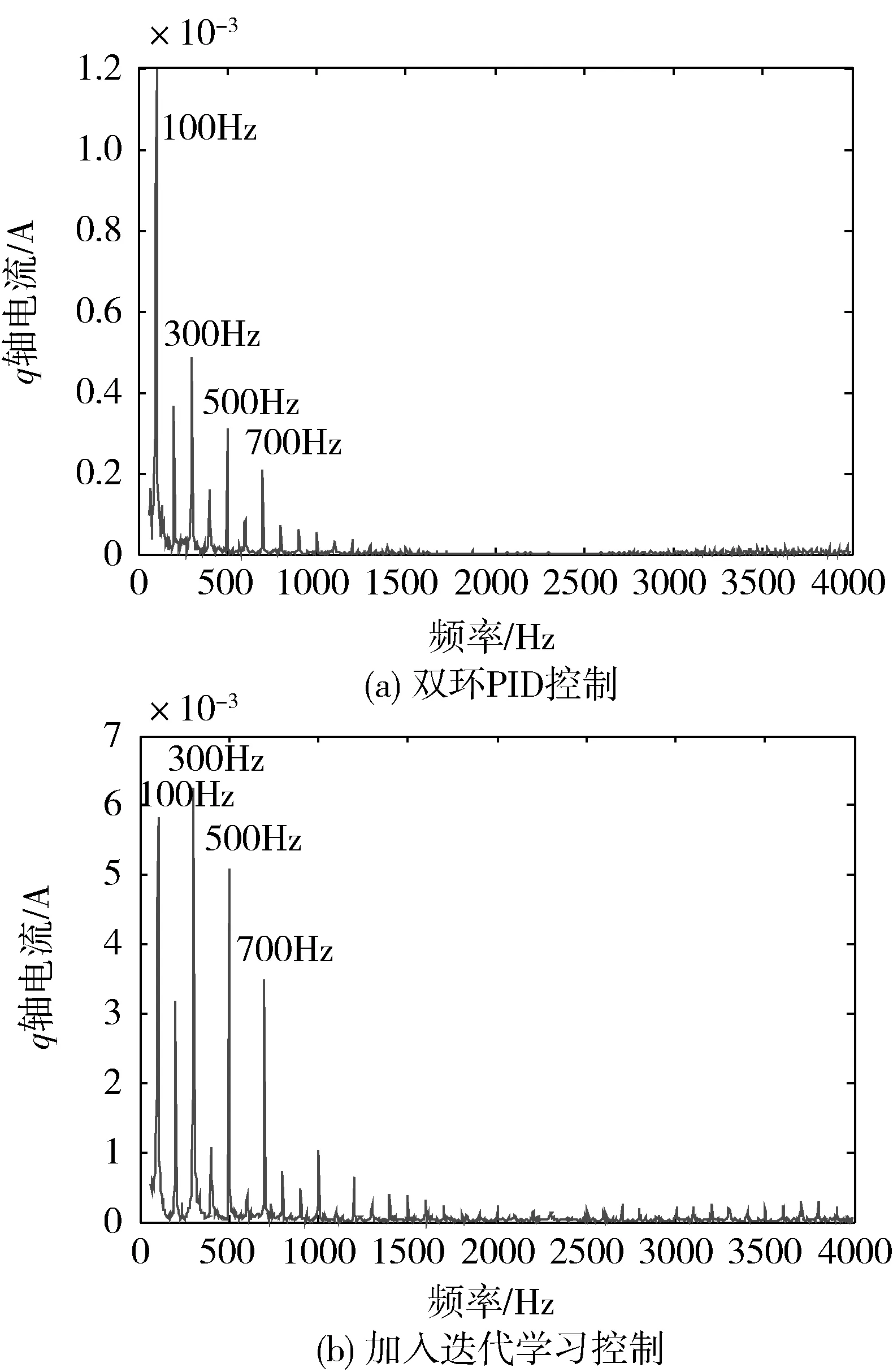
图7 q轴电流频谱分析Fig.7 Frequency domain analysis on q-axis current

从上述仿真结果可以看出，迭代学习控制算法的加入，可以有效的抑制CMG高速转子动不平衡作用在低速框架上的扰动力矩，使得框架输出转速波动量大幅度降低，提高了CMG输出力矩的精度.

4 结 论

本文对作用在CMG低速框架的扰动力矩进行了分析，通过结合理论公式与试验实测结果，建立了低速框架系统的较为准确的高速转子动不平衡扰动力矩模型.为了消除扰动力矩对CMG框架控制精度的影响，在传统的PID双环控制系统上嵌入了迭代学习的算法模块.仿真结果表明，这种新的控制方法，能够有效地抑制周期性波动的动不平衡扰动力矩，降低CMG框架的转速波动，从而大幅提高CMG输出力矩的精度.

[1] ARENA L, DELFINI A. Design manufacturing and ground test of a small and cost effective FPGA-based control moment gyro for the URSA MAIOR Nano-satellite[C]// Proceedings 65th International Astronautical Congress. Toronto, Canada: IAF, 2014:1-8.

[2] MUMM E, DAVIS K, MAHIN M, et al. Miniature control moment gyroscope development[C]// Proceedings of Aerospace Conference. MT: IEEE, 2014:1-9.

[3] 鲁明，李耀华，张激扬，等. 控制力矩陀螺框架伺服系统的超低速测速方法[J].中国惯性技术学报, 2012,20(4):234-238. LU M, LI Y, ZHANG J, et al. Ultra-low speed detection method for CMG gimbal servo systems[J]. Journal of Chinese inertial Technology, 2012,20(4):234-238.

[4] ZHOU D, ZHAI B, WEI D, et al. The design, ground test and flight validation of a high accuracy servo scheme for control moment gyroscope application[J]. Automatic Control in Aerospace, 2013,19(1):476-481.

[5] ZHANG Y, ZHU J. Direct torque control of permanent magnet synchronous motor with reduced torque ripple and commutation frequency[J]. IEEE Transactions on Power Electronics, 2011,26(1):235-248.

[6] XU J, PANDA S, PAN Y, et al. A modular control scheme for PMSM speed control with pulsation torque minimization[J]. IEEE Transactions on Industrial Electronics, 2004,51(3):526-536.

[7] QIAN W, PANDA S, XU J. Torque ripple minimization in PM synchronous motor using iterative learning control[J]. IEEE Transactions on Power Electronics, 2004,19(2):272-279.

[8] 陈茂盛, 金光，张涛等.积分反馈自抗扰控制力矩陀螺框架伺服系统设计[J].光学 精密工程，2012, 20(11): 2424-2432. CHEN M, JIN G, ZHANG T, et al. Design of gimbal servo system of CMG using active disturbance rejection control with integral feedbacks[J]. Optics and Precision Engineering, 2012, 20(11): 2424-2432.

[9] 吴忠，张激扬. 控制力矩陀螺框架伺服系统动力学建模与控制[J]. 应用基础与工程科学学报，2007,15(1):130-146. WU Z, ZHANG J. Dynamics and control of gimbal servo systems for control moment gyroscopes[J]. Journal of Basic Science and Engineering, 2007,15(1):130-146.

[10] 金磊，徐世杰. SGCMG框架伺服系统动力学建模与低速控制[J]. 中国空间科学技术，2010,6:1-10. JIN L, XU S. Dynamics modeling and low rate control of gimbal servo system for single gimbal control moment gyro[J]. Chinese Space Science and Technology, 2010,6:1-10.

Disturbance Torque Minimization Strategy for Control MomentGyroscopes Based on Iterative Learning Algorithm

LAI Lin， ZHOU Daning， WU Dengyun

(Beijing Institute of Control Engineering， Beijing 100190, China)

For high-agility and high-precision attitude maneuver of remote sensing satellites, the control moment gyroscope (CMG) is expected to supply more accurate torque, which means the disturbance torque acting on its gimbal axis should be minimized to reduce the fluctuation of the gimbal speed. The torque generated by the wheel imbalance is analyzed, and the gimbal system model is built. To improve the gimbal speed stability, an iterative learning control (ILC) module is inserted into the PID gimbal control system. The proposed control system is evaluated via system simulation, and the results demonstrate that the ILC algorithm can minimize the fluctuating torque effectively, which significantly improves the precision of the CMG output torque.

CMG； iterative learning； pulsation torque minimization

*国家自然科学基金青年科学基金资助项目(11402019).

2014-12-20

V448.2

A

1674-1579(2015)06-0042-05

10.3969/j.issn.1674-1579.2015.06.008

来 林(1983—)，男，工程师，研究方向为惯性执行机构设计；周大宁(1977—)，男，高级工程师，研究方向为惯性执行机构设计；武登云(1974—)，男，研究员，研究方向为惯性执行机构设计.