综合考虑宏细观缺陷的岩体动态损伤本构模型*

张 力 民,吕 淑 然,刘 红 岩

(1.北京 科技大学土 木与环境工 程学院,北 京 100083; 2.河北承德钢铁公司,河北 承德067000; 3.首都经济贸易大学安全与环境工程学院,北京100026; 4.中国地质大学(北京)工程技术学院,北京100083; 5.西藏大学工学院,西藏 拉萨850000; 6.中国地质大学(北京)国土资源部深部地质钻探技术重点实验室,北京100083)

综合考虑宏细观缺陷的岩体动态损伤本构模型*

张 力 民1,2,吕 淑 然3,刘 红 岩4,5,6

(1.北京 科技大学土 木与环境工 程学院,北 京 100083; 2.河北承德钢铁公司,河北 承德067000; 3.首都经济贸易大学安全与环境工程学院,北京100026; 4.中国地质大学(北京)工程技术学院,北京100083; 5.西藏大学工学院,西藏 拉萨850000; 6.中国地质大学(北京)国土资源部深部地质钻探技术重点实验室,北京100083)

针对节理岩体同时含有节理、裂隙等宏观缺陷及微裂隙、微孔洞等细观缺陷的客观事实,提出了在节理岩体动态损伤本构模型中应同时考虑宏细观缺陷的观点。为此,首先对基于细观动态断裂机理的经典岩石动态损伤本构模型—TCK(Taylor-Chen-Kuszmaul)模型进行了阐述,其次基于 Lemaitre等效应变假设推导了综合考虑宏细观缺陷的复合损伤变量(张量),进而在此基础上建立了相应的节理岩体动态损伤本构模型,并利用该模型讨论了载荷应变率及节理条数对岩体动态力学特性的影响规律。结果表明,在不同载荷应变率下试件在变形初始阶段是重合的,而后随着应变的增加,试件峰值强度、峰值应变及总应变均随载荷应变率的增加而增加;随着节理条数的增加,试件峰值强度逐渐降低,但降低趋势逐渐变缓并趋于某一定值。上述研究结论与目前的理论及实验研究结果的基本规律是一致的,说明了本模型的合理性。

爆炸力学;动态损伤本构模型;宏观缺陷;细观缺陷;动态断裂机理;复合损伤变量;节理岩体

自然界中的岩体是由节理、裂隙等宏观地质结构面和被其切割而成的岩石块体所组成,而宏观完整岩石又是由多种矿物颗粒胶结而成,因此其内部必然存在大量的微裂纹、微孔洞等细观缺陷。所以岩体是同时含有微裂纹、微孔洞等细观缺陷(细观损伤)及节理、裂隙等宏观缺陷(宏观损伤)的复合损伤地质材料,这两类损伤也分别以不同的作用机理对岩体力学特性产生影响。基于岩石爆破的实际需要,B. Budiamsky等[1]采用细观力学对岩石中弥散分布的裂 纹 群 进行了分析,并建立 了 相 应的岩石爆破 损 伤模型,该模型也成为岩石爆破理论模型乃至整个岩石动力学模型的发展方向之一。D.E.Grady等[2]认为岩石中含有大量服从双参数 Weibull分布的原生裂纹,在外载下,其中一些裂纹被激活并扩展,由此提 出 了 岩 石 爆 破 各 向 同 性 损 伤 模 型 ,即 GK 模 型 。L.M.Taylor等[3]引 进 R.J.O’connell等[1]的 有 效 体积模量和泊松比与微裂纹密度的关系表达式和 D.E.Grady等[2]给出的碎块尺寸表达式,建立了损伤变量与裂纹密度之间的关系式,并将损伤变量以率形式耦合到动态本构方程中从而建立了著名的 TCK模型。而后,又有 不少学 者从岩 石的细 观动态 断裂角 度提出 了多种 损伤本 构模型[4-7]。

上述本构模型由于没有考虑岩体中存在的节理、裂隙等宏观缺陷,因此仅能用于描述宏观上相对完整的岩石。为此,不少学者基于波传播理论对节理岩体的动态损伤本构模型进行了研究,如 Li Jianchun等[8]基 于 粘 弹 性 理 论 ,提 出 了 含 1 组 平 行 节 理 的 岩 体 动 态 等 效 连 续 介 质 模 型 。 李 宁 等[9]通 过 分 析单组裂隙细观特征对应力波传播特性的影响机理,提出了表达裂隙细观特征对波速影响的半连续介质动力损伤模型。但是上述2种模型虽然考虑了节理等宏观缺陷,但是却没有同时考虑存在于完整岩块内部的微裂隙等细观缺陷,而微裂隙等细观缺陷是不会因为节理等宏观缺陷的存在而消失。因此迄今为止,理论界还没有提出一种能够同时反映上述2种不同尺度缺陷对岩体力学性质影响的动态损伤本构模型。而相 关实验 表明[10]岩体内同时存在的宏细观损伤均对岩体的 力 学 性 质 产 生 影 响,且 它 们 之 间还可能存在着复杂的相互作用。因此,如何更好地同时反映这两类缺陷对岩体动态力学性质的影响则是目前岩体动态损伤力学研究中一个亟待解决的重要课题。外载下岩体内的初始细观损伤可以发展成为宏观损伤,而且从损伤的尺度与损伤识别的尺度来看,岩体的宏观损伤与细观损伤之间并无严格界限,通常与所研究问题的尺度有关。但是,为了工程分析方便,对岩体的宏观和细观损伤进行分类研究,然后进行耦合计算分析是十分必要的[11]。

本文中在首先对基于细观损伤机理的经典岩石动态损伤本构模型(TCK模型)进行阐述的基础上,根据 Lemaitre应变等效假设建立综合考虑宏细观缺陷的损伤变量(张量),并由此建立相应的岩体动态损伤本构模型。

1 岩石细观动态损伤的TCK模型

如前所述,TCK 模型提出后获得了学术界的广泛认可。因此下面就以该模型为基础,对岩石细观动态损伤模型的建立过程进行探讨。

研究表明,岩石动态强度与破坏特性与其内部缺陷分布有关,在外载下岩石内部微裂纹将发生扩展、演化甚至贯通,进而导致其发生破坏。对岩石动态力学特性的描述可用介于0~1之间的损伤标量ω来描述。则岩石在受载下的弹性能W为:

式 中 :E为 岩 石 材 料 的 固 有 弹 性 模 量 ,ε为 应 变 。

根据岩石微观断裂理论,损伤标量ω可表示为:

式 中:N为 单 位 体 积 岩 石 中 理 想 片 状 圆 形 缺 陷 数;是 围 绕 半 径 为r的 缺 陷 球 状 区 域 。 因 此 ,ω也表示岩石单位体积里所包含的裂纹缺陷体积。

D.E.Grady等[12-13]研 究 岩 石 脆 性 断 裂 缺 陷 分 布 时,假 定 裂 纹 密 度 服 从 Weibull分 布:

式中:n为应变ε水平以下缺陷数目,常数k和m 表征断裂活动的材料性质。

由应变增量dε引起的缺陷数增量为:

由于初始损伤的影响,岩石中实际参加活动的缺陷数为:

在某一时刻t,裂纹扩展取决于经历的时间t-τ及应变ε(t),这里假定裂纹活化取决于裂纹的扩展速度cg,因此有:

裂纹扩展速度是岩石断裂的一个重要特性,它控制着岩石动态断裂时的损伤率,损伤表达式为:

考 察 应 变 率 对 岩 石 动 态 断 裂 强 度 的 影 响 ,假 定 岩 石 断 裂 时 的 应 变 取 决 于 应 变 速 率ε(t)=εtε为 常应变速率,因此损伤率的变化为:

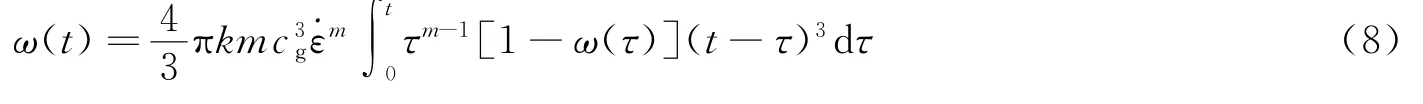
式(8)省略高阶项后可简化为:

由此可得岩石单轴压缩动态本构关系即应力与应变及应变率的关系为:

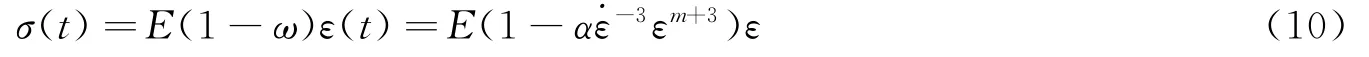
在该模型中需要确定的参数有裂纹扩展速度cg、k和m。研究表明裂纹扩展速度约等于理论瑞利波波 速cR的 0.34~0.66 倍 ,cR≈ 0.58cL,cL为 弹 性 纵 波 速 度 )。 若 取 裂 纹 扩 展 速 度 约 等 于 理 论 瑞 利 波波速的0.5倍,则cg=0.29cL。k、m是损伤模型引入的2个重要的岩石参数,参数m把岩石材料的极限拉伸应力和应变率联系起来,D.E.Grady等[12-13]研究认为 m为 常数,并建议 m=6。材料 参数k的定义和物理意义尚不明确,k值的确定由不同应变率的拉伸断裂实验得出,到目前 为 止,仅有美国 Sandia国家实验室提供了1组油母页岩的实验数据,L.M.Taylor等[3]认为在恒应变率拉伸条件下:

式 中 :pm为 常 应 变 率 下 的 岩 石 最 大 抗 拉 强 度 ,K 为 体 积 模 量 ,KIC为 岩 石 断 裂 韧 性 ,θ为 体 积 应 变 ,ρ为 岩石密度,其余参数同前。

2 考虑宏细观损伤耦合的岩体动态损伤本构模型

2.1 仅考虑宏观缺陷的岩体损伤本构模型

节理等宏观缺陷将导致岩体力学性质的弱化及各向异性,为反映这种影响,目前常采用损伤理论进行研究。假定损伤后的岩体本构关系仍服从胡克定律,则节理对岩体的损伤就体现为弹性常数的弱化,即节理岩体的弹性常数与损伤张量之间的关系,可以表示为:

式 中 :E0、E分 别 为 完 整 岩 块 和 节 理 岩 体 的 弹 性 张 量 ;I为 单 位 张 量 ,χ为 节 理 岩 体 损 伤 张 量 。

节理岩体损伤本构模型的研究就归结为损伤张量的计算。下面以平面二维问题为例,讨论节理岩体损伤张量计算方法。目前常用二阶张量描述岩体的各向异性损伤,许多学者基于不同角度也提出了多 种 定 义 方 法 。T.Kyoya等[14]和 T.Kawamoto等[15]将 含 有 1组 平 行 节 理 的 岩 体 损 伤 张 量 定 义 为 :

式 中 :l为 节 理 平 均 间 距 ,V 为 样 本 体 积 ,N 为 样 本 中 节 理 数 ,ak为 样 本 中 第k条 节 理 表 面 积 ,nk为 样 本中第k条节理表面上的单位法向矢量。

孙 卫 军 等[16]假 定 节 理 面 是 一 个 无 厚 度 、二 维 延 展 的 圆 盘,应 用 岩 体 结 构 的 概 率 统 计 模 型 ,可 以 估 算节理岩体的损伤张量。例如对于第i组节理,建议用下式表示其损伤张量:

式中:λi为第i组节理面密度,di为 第i组 节理平 均直径 ,一般 取为平 面上的 迹长;ni为第i组节理的单位法向矢量。同时还有其他一些学者也提出了类似的节理岩体损伤变量计算方法。

2.2 宏细观缺陷耦合的损伤变量计算方法

根据损伤理论,损伤变量的定义是损伤模型建立的前提和基础,因此下面首先讨论同时考虑宏细观缺陷的节理岩体损伤变量计算方法。工程岩体总是包含着节理、裂隙的宏观损伤特性和节理间岩石的细观损伤特性,这 2种不 同尺度 损伤缺 陷的耦 合集中 表现为 损伤变 量的耦 合[11]。

在计算节理岩体损伤变量的耦 合 时,采 用 如 下 基 本 假 设[11]:(1)宏 观 损 伤 与 细 观 损 伤 以 人 的 肉 眼可见与不可见划分,并认为宏观损伤为各向异性损伤,而细观损伤为各向同性损伤。(2)在描述岩体损伤时,细观损伤和宏观损伤分别采用不同的描述方法,具体见前文。(3)在考虑宏细观损伤耦合时应遵循损伤力学基本假设——Lemaitre假设[17],即应变等效原理进行耦合,而不 能将2 种损伤 简单叠 加。

损伤耦合的条件是在一定应力作用下,2种损伤分别引起的损伤应变之和等于耦合损伤引起的应变量,如图1所示,假设图1(a)~(d)分别为同时含有宏观和细观损伤的岩体、仅含宏观损伤 的岩体、仅含细观损伤的岩体及完全不含损伤的岩体,其弹性模量分别为:E12、E1、E2和E0,其在外力σ0作用下产生 的 应 变 分 别 为 :ε12、ε1、ε2、ε0,那 么 根 据 Lemaitre应 变 等 效 假 设 ,则 有 :

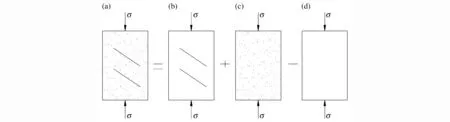
图1 应变等效计算示意图Fig.1 Calculation of the equivalent strain

若假设宏、细观损伤在荷载作用方向上的损伤变量分别为D1、D2及其耦合损伤变量为 D12,则有:

所以有:

由 Lemaitre假设知:

将式(15)代入式(14),并经过整理后可得:

对于2种极端情况,即岩体仅含宏观损伤时,那么将 D2=0代 入式(18)可得 D12=D1,即此时 岩 体的耦合损伤变量等于其宏观损伤变量,符合实际情况。同样当岩体仅含微观损伤时,D1=0,可得 D12= D2,即此时岩体的耦合损伤变量等于其细观损伤变量,也符合实际情况。这说明通过该方法建立的宏细观耦合损伤变量是合理的。

同样基于 Lemaitre假设,杨更 社等[11]经过 推导认 为岩体 的宏细 观耦合 损伤变 量为:

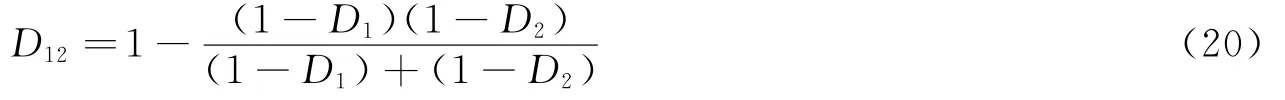
可 以 看 出,对 于 式(19)当D1=0时,,即,也 就 是 说 当 岩 体 内 仅 含 细 观 损 伤时,岩体的总损伤变量即耦合损伤变量并不等于细观损伤变量,显然不符合实际情况。通过对其推导过程的分析认为,假设ε12=ε1+ε2,是重复计算了1次完全无损伤弹性体产生的应变,即没有减去图1(d)所 产 生 的 应 变,因 而 所 得 结 果 也 不 甚 合 理 。 而 刘 红 岩 等[18]认 为 岩 体 宏 细 观 耦 合 损 伤 变 量 为:D12=D1+D2-D1D2,但从建立过程来看,该方法缺乏严格的理论基础。

对上述3种不同宏细观耦合损伤变量的计算结果进行对比分析,如图2所示。

由图2所示的变化规律可以看出,曲线1是由本文中方法计算出的耦合损伤变量,其值最小,而随着宏细观损伤变量的增加,由文献[18]中方法计算出的耦合损伤变量(曲线2)逐渐大于由文献[11]中方法的计算结果(曲线 3)。这说 明文献 [11,18]所提出的方法过大地估计了宏细观损伤的耦合影响,分析认为产生这种情况的主要原因是由于文献[11]过大地估计了由损伤产生的应变,而文献[18]则缺乏相应的理论基础,因此认为本文提出的计算方法较为合理。

由于宏观损伤具有奇异性,上面所采用的D1仅为荷载作用方向上的损伤变量值,因此必须对张量化以反映岩体宏观损伤的各向异性。张量化的 方 法 很 多,在 此 采 用 T.Kawamoto等[15]的 方 法,引 入 损伤张量Ω,则Ω=D1N,其中N是一个二阶对称张量,其计算方法为:

图2 耦合损伤变量随宏细观损伤变量变化规律Fig.2 Change law of the coupled damage variable varied with macroscopic and mesoscopic damage

(1)对于含单组非贯通裂隙的岩体,假定非贯通裂隙的法向与x轴夹角为β,如图3所示,设该组非贯通裂隙的单位法向矢量为n,则 有

(2)对 于 含 2 组 以 上 非 贯 通 裂 隙 的 岩 体,N的 计 算 方 法是:设岩体 中 有 M 组 非 贯 通 裂 隙,其 单 位 法 向 矢 量 分 别 为n(m)(m=1,2,… ,M),而

根据上述方法,对式(19)进行张量化,若假设节理等宏观缺陷引起的损伤张量为Ω、微裂纹等细观缺陷引起的损伤变量为D,那么这2种不同尺度的缺陷所引起的耦合损伤变量Ω12为:

图3 含裂隙岩体的受力模型Fig.3 Mechanical model of cracked rock mass

2.3 基于岩石细观动态损伤本构模型的岩体动态损伤本构模型

当仅考虑岩石中存在的微裂纹等细观缺陷时,前人已建立了如式(10)所示的岩石细观动态损伤本构模型。但是由于工程岩体都含有节理、裂隙等宏观缺陷,因此如何根据岩石细观动态损伤本构模型的研究思路建立节理岩体的动态损伤本构模型则是一个亟待解决的重要问题。

由损伤理论可知,当岩体内同时含有宏、细观等2种不同尺度的缺陷时,在损伤模型中则体现为损伤变量的变化。根据这一思路,把 式(10)中 的 损 伤 变 量ω(t)用 式(20)中 耦 合 损 伤 变 量 Ω12替 换 即 可 ,而其中的细观损伤变量D则相应地用ω(t)来替换,即可得到节理岩体的单轴动态损伤本构方程为:

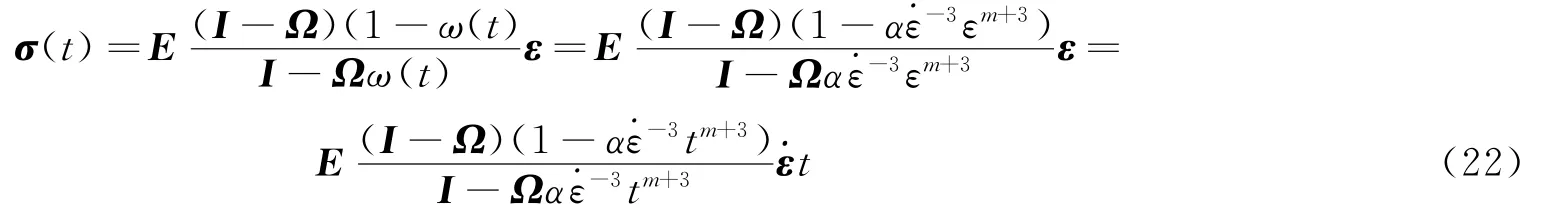
3 算例分析

岩石试件的二维计算模型取为如图4所示,模型上部受到动荷载σd的作用,下部固定。模型中含有一条贯通的45°节理,那么它将对岩体产生宏观的各向异性损伤,这里采用式(13)计算其损伤变量,裂隙的外法线方向为计 算 可 得 其 损 伤 张 量 为:Ω =为 了 与 完 整 岩 石 进 行 对 比 分 析,这 里 同 时 对 节 理 岩 体 与 完 整 岩 石 的 应 力 应 变 曲 线进行计算,除节 理参数 外,二 者的其 余参数 取值均 相同。 由于 TCK 模 型中的k、m等参数 是 由 动 态 拉 伸断 裂 实 验 确 定,为 此 借 鉴 L.M.Taylor 等[3]的 实 验 资 料 。 即 认 为 当 岩 石 的 杨 氏 弹 性 模 量 为 10.8 GPa、体 积 模 量 为 6 GPa,泊 松 比 为 0.2,塑 性 屈 服 应 力 为 200 MPa,密 度 为 2 270 kg/m3,断 裂 韧 性 为1.0 MPa·m1/2,及 应 变 率 分 别 为 102s-1时,k和m 可 分 别 取 为 5.12×1022 m-3和 7。 根 据 前 述 讨 论 ,可 取 裂 纹 的 扩 展 速 度,计 算 可 得 裂 纹 扩 展 速 度 为666.7 m/s。 按照平面应力问题进行求解。根据上述参数,可得节理岩体与完整岩石的单轴压缩动态曲线如图5所示。

图4 岩石试件二维计算模型Fig.4 Two-dimensional calculation model of rock

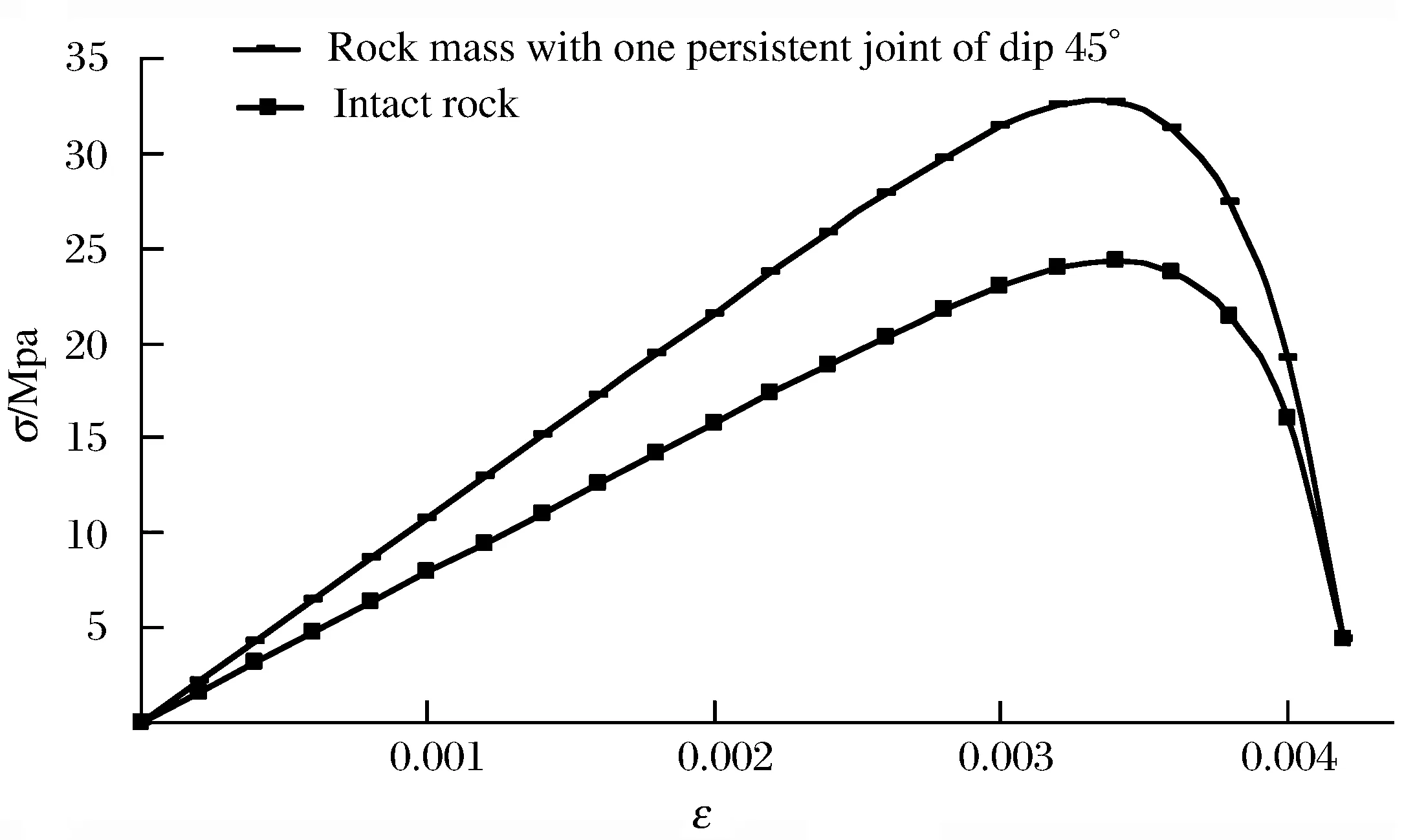
图5 岩体单轴压缩动态应力应变曲线Fig.5 Stress-strain curves of rock under axial dynamic compression

由图5可以看出:(1)从曲线形态上来看,当岩石内部仅含有微裂纹等细观损伤时,基于微裂纹扩展演化的细观动态损伤本构模型能够很好地反映岩石动态应力应变曲线特征,而基于此建立的节理岩体动态损伤本构模型也包含了应力应变曲线的线性段、峰值段及破坏软化阶段。(2)从试件峰值强度来看,当岩体内含有节理裂隙等宏观缺陷时,其力学性质明显软化,表现为峰值应力有所减小。对本算例而言,节 理 岩 体的 峰 值 应 力 为 24.35 MPa,而 相 应完 整 岩 石 的 峰 值强 度 则 为 32.71 MPa,因 此 仅 为 其74.4%,这说明宏观损伤即节理的存在将在一定程度上削弱了岩体峰值强度,即表明宏、细观两种不同尺度的缺陷对岩体的强度均有影响。(3)从试件的应变大小来看,节理岩体的总应变明显大于完整岩石的应变,这说明节理岩体在压缩荷载作用下不仅岩石块体产生压缩变形而且试件还将沿节理面发生剪切滑移及压缩变形,因而相对于完整岩石试件,相应的节理岩体试件将发生更大的变形,进而产生较大的应变。因此,认为节理存在还降低了试件刚度,增大了其柔性。

3.1 载荷应变率对岩体动态力学特性的影响

载荷应变率对岩体力学特性及强度也有很大影响,下面利用上文中提出的模型研究载荷应变率对单节理岩体试件力学特性的影响。采用的计算模型仍为图4所示,取载荷应变率分别为100、200和300 s-1,其余计算参数同上。计算结果如图6所示。首先由图6可以看出,在不同载荷应变率下试件在应变较小时即在弹性变形阶段是重合的,同时随着载荷应变率的增加,试件峰值强度逐渐变大、对应的峰值应变及总应变也随之增加,这与于亚伦[19]对完 整 岩 石 在 不 同 载 荷 应 变 率 下 得 到 的压缩应力应变曲线的变化规律是一致的。这说明节理岩体动态力学特性与完整岩石同样具有应变率效应,只是二者对应变率效应的响应程度会存在一定差异。同时在应变率为 100~ 300 s-1范围内,节理岩体的峰值强度随应变率的增加近似成线性增长。

3.2 节理条数对岩体动态力学特性的影响

节理条数对岩体力学特性及强度也有很大影响,下面利用本文所提出的模型对多节理岩体试件的力学特性及强度等进行了研究,采用的计算模型仍为图4所示,取平行节理条数为1~4条,计算结果如图7所示。可以看出:(1)随着节理条数增加,岩体应力应变曲线斜率降低,这说明岩体弹性模量随着节理条数的增加而降低,即节理岩体刚度减小、柔性增大;(2)随着节理条数增加,岩体峰值强度逐渐降低,当节理条数为1~4条时,对应的岩体峰值强度分别为24.35、19.94、18.17 和 17.09 MPa,相 比 相应完整岩石的峰值强度32.71 MPa均有不同程度的下降,且随节理条数的增加,试件峰值强度的下降趋势逐渐变缓。同时从下降幅度来看,当节理条数由1条增加到2条时,强度下降幅度最大,而当增加到3、4条时,强度下降幅度明显减小,这说明节理之间存在着相互作用,作用结果将导致岩体的总体强度更加弱化,与节理岩体的静力学特性一样不符合单纯的线性组合原理。因此,该计算结果也从另一侧面说明本文所提出的模型是合理的。

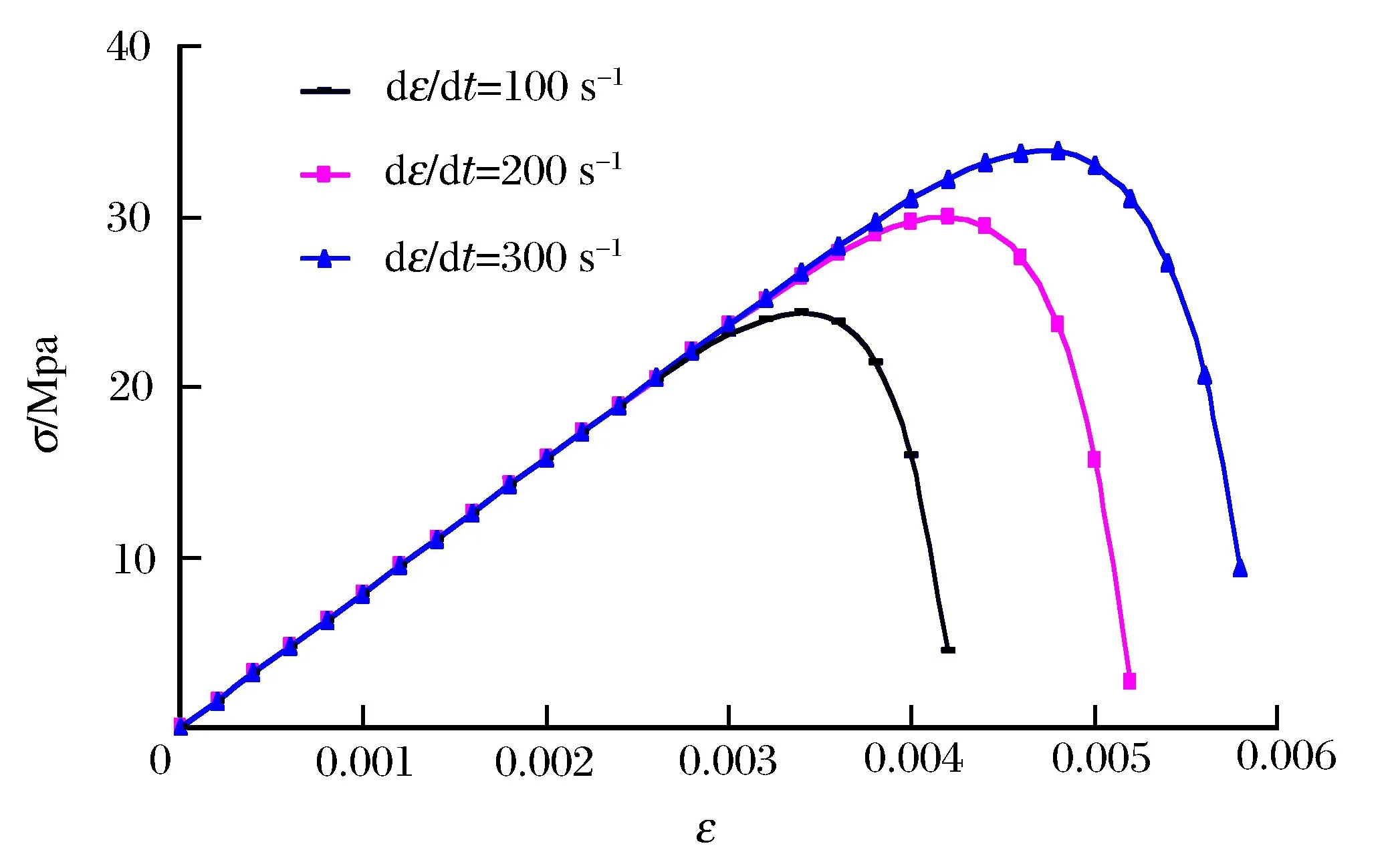
图6 不同应变率下试件动态应力随应变变化关系Fig.6 Relation between dynamic stress of rock varied with strain under different load strain rates

图7 1~4条平行节理试件应力应变曲线Fig.7 Stress-strain curves of the jointed rock mass with 1~4 parallel joints

4 结 论

(1)根据动载下微裂纹的扩展机理,介绍了仅考虑细观缺陷的岩石动态损伤 TCK 本构模型。

(2)根据 Lemaitre应变等效假设,推导了同时 考 虑 宏 细观缺陷的 损 伤 变 量(张 量)。然后采用 能 够同时反映宏、细观缺陷的损伤变量(张量)替换 TCK模型中仅考虑细观缺陷的损伤变量,由此建立了综合考虑宏、细观缺陷的节理岩体动态损伤本构模型,该模型同时考虑了载荷应变率及宏、细观两类不同尺度缺陷对岩体动态力学特性影响。

(3)利用建立的本构模型讨论了节理岩体与完整岩石动态应力应变曲线的差异,说明了节理等宏观缺陷对岩体动态特性的影响,就本文算例而言,当岩体中含有一条倾角为45°的贯通节理时,其峰值应力仅为相应完整岩石的74.4%。然后利用该模型讨论了载荷应变率及节理条数对岩体动态力学特性的影响规律,所得结果与相关已有研究成果的基本规律是一致的,说明了模型的合理性。

[1]Budiansky B,O’Connell R J.Elastic moduli of a cracked solid[J].International Journal of Solids Structures,1976,12(2):81-97.

[2]Grady D E,Kipp M L.Continuum modeling of explosive fracture in oil shale[J].International Journal of Rock Mechanics and Mining Sciences,1980,17(3):174-157.

[3]Taylor L M,Chen E P,Kuszmaul J S.Microcrack induced damage accumulation in brittle rock under dynamic loading[J].Computer Method in Applied Mechanics&Engineering,1986,55(3):301-320.

[4]Zuo Q H,Disilvestro D,Richter J D.A crack-mechanics based model for damage and plasticity of brittle materials under dynamic loading[J].International Journal of Solids and Structures,2010,47(2):2790-2798.

[5]Zhou X P,Yang H Q.Micromechanical modeling of dynamic compressive responses of mesoscopic heterogenous brittle rock[J].Theoretical and Applied Fracture Mechanics,2007,48(1):1-20.

[6]Wang Zhi-liang.Li Yong-chi,Wang J G.A damage-softening statistical constitutive model considering rock residual strength[J].Computers&Geosciences,2007,33(1):1-9.

[7]Tang C A,Liu H,Lee P K K,et al.Numerical studies of the influence of microstructure on rock failure in uniaxial compression:PartⅠ:Effect of heterogeneity[J].International Journal of Rock Mechanics&Mining Sciences, 2000,37(4):555-569.

[8]Li Jian-chun,Ma Guo-wei,Zhao Jian.An equivalent viscoelastic model for rock mass with parallel joints[J].Journal of Geophysical Research,2010,115(B3):1-10.

[9]李宁 ,张平 ,段 庆伟,等.裂隙岩 体的细观动 力损伤模型[J].岩石力 学与 工程学 报,2002,21(11):1579-1584. Li Ning,Zhang Ping,Duan Qing-wei,et al.Dynamic meso-damage model of jointed rockmass[J].Chinese Journal of Rock Mechancis and Engineering,2002,21(11):1579-1584.

[10]刘 红岩,邢闯 锋,刘 冶,等.宏 微观缺陷对 岩体力学特 性影响规律 试验研究[J].自 然灾害 学报 ,2013,2(5):134-139. Liu Hong-yan,Xing Chuang-feng,Liu Ye,et al.Test study on the law of macro and micro flaws effects on the mechanical properties of rockmass[J].Journal of Natural Disaster,2013,2(5):134-139.

[11]杨更社,谢定义.岩体宏观细 观损 伤 的 耦 合计 算 分 析 [C]∥ 第 六 次 全 国 岩 石力 学 与 工 程学 术 大 会论 文 集.武 汉, 2000:327-329.

[12]Grady D E,Kipp M E.Continuum modeling of explosive fracture in oil shale[J].International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts,1987,17(3):147-157.

[13]Grady D E,Kipp M E.The micromechanics of impact fracture of rock[J].International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts,1979,16(5):293-302.

[14]Kyoya T,Ichikawa Y,Kawamoto T.A damage mechanics theory for discontinuous rock mass[C]∥Proceedings of the 5th International Conference on Numerical Methods in Geomechanics.Nagoya,Japan,1985:469-480.

[15]Kawamoto T,Ichikawa Y,Kyoya T.Deformation and fracturing behavior of discontinuous rock mass and damage mechanics theory[J].International Journal of Rock Mechanics and Mining Sciences&Geomechanics Abstracts, 1988,25(4):1-30.

[16]孙 卫军,周维 垣.裂 隙岩体弹塑 性-损伤本构模 型[J].岩石 力学与工程 学报,1990,2(9):108-119. Sun Wei-jun,Zhou Wei-yuan.An Elasto-plastic damage mechanics constitutive model for jointed rockmass[J]. Chinese Journal of Rock Mechanics and Engineering,1990,2(9):108-119.

[17]Lemaitre J.A course on damage mechanics[M].Spring-Verlag,1996.

[18]刘红岩 ,吕 淑然,丹增 卓玛,等.节理岩 体宏微观损 伤耦合的三 维本构模型 研究[J].水 利 与 工 程 学 报,2013,11(3): 85-88. Liu Hong-yan,LüShu-ran,Danzeng Zhuo-ma,et al.Study on 3-D constitutive model for jointed rock mass by coupling macroscopic and microscopic damge[J].Journal of Water Resources and Architectural Engineering, 2013,11(3):85-88.

[19]于 亚伦.用三 轴 SHPB 装置研究岩 石的动载特 性[J].岩土 工程学报,1992,14(3):76-79. Yu Ya-lun.Study on the dynamic characteristic of rock by tri-axial SHPB[J].Chinese Journal of Geotechnical Engineering,1992,14(3):76-79.

A dynamic damage constitutive model of rock mass by comprehensively considering macroscopic and mesoscopic flaws

Zhang Li-min1,2,LüShu-ran3,Liu Hong-yan4,5,6(1.Civil and Environmental Engineering School,University of Science and Technology Beijing, Beijing 100083,China; 2.Hebei Chengde Iron and Steel Corporation,Chengde 850000,Hebei,China; 3.School of Safety and Environment Engineering,Capital University of Economics and Business, Beijing 100083,China; 4.College of Engineering&Technology,China University of Geoseiences(Beijing), Beijing 100083,China; 5.School of Engineering,Tibet University,Lasa 850000,Xizang,China; 6.Key Laboratory on Deep Geo Drilling Technology,Ministry of Land and Resources, China University of Geoseiences(Beijing),Beijing 100083,China)

In view of the fact that the jointed rockmass contains both macroscopic flaws such as the joint and crack and the mesoscopic flaws such as the microcrack and microhole,the viewpoint that the above two kinds of flaws should be considered at the same time in the dynamic damage constitutive model of the jointed rockmass is proposed.Therefore,the rock classic dynamic damage constitutive model namely TCK model based on mesoscopic dynamic fracture mechanism is discussed,then the compound damage variable(tensor)comprehensively considering macroscopic and mesoscopic flaws based on Lemaitre equivalent strain hypothesis is deduced.Finally,the corresponding dynamic damage constitutive model is established,and the effect law of the load strain ratio and joint set on rock mass dynamic mechanical property is discussed with this model.The results show that under different load strain rates,the initial deformation stage of the samples coincides with each other,and then with increase of strain,the climax strength,strain and the total strain of the samples all increase.With increase in joint sets,the climax strength of the samples gradually decreases,but the reduction degree gradually becomes little and tends to a certain value.The basic law between the above research conclusions and the current experimental and theoretical results is the same,which demonstrates the rationality of this model.

mechanics of explosion;dynamic damage constitutive model;macroscopic flaw;mesoscopic flaw;dynamic fracture mechanism;compound damage variable;jointed rock mass

O383;TJ410.33国标学科代码:13035

:A

10.11883/1001-1455-(2015)03-0428-09

(责任编辑 王易难)

2013-10-30;

2013-12-20

国家 自然科学基 金项目(41002113,41162009);教育 部科学技术 研究重点项 目(211175);

中央高校基本科研业务费专项资金项目(2010ZY45);

2011年度北京市属高等学校人才强教深化计划人才创新团队项目(PHR201107143)

张 力 民(1970— ),男 ,博 士 ; 通 讯 作 者 :刘 红 岩 ,lhyan1204@126.com。