中国造船企业的量子Stackelberg博弈与国际竞争＊

杨 戟 冯卫东 冯影影 王 霞

（1.华中科技大学文华学院数学建模实验室 武汉 430074）（2.武汉数字工程研究所 武汉 430205）（3.武汉信息传播职业技术学院基础科学部 武汉 430223）

中国造船企业的量子Stackelberg博弈与国际竞争＊

杨 戟1冯卫东2冯影影3王 霞1

（1.华中科技大学文华学院数学建模实验室 武汉 430074）（2.武汉数字工程研究所 武汉 430205）（3.武汉信息传播职业技术学院基础科学部 武汉 430223）

近三十年来中国船舶工业取得了巨大的成就，年造船吨位的世界排名由第十七位上升到前三位，大量先进设施的投入使用及对日韩造船技术的学习使生产效率大大提高。我国造船企业必须在提高核心竞争力的同时，努力收集各种“竞争情报”以便在复杂的国际造船业竞争中能做出正确的决策，提高国际竞争力。论文结合Stackelberg博弈的理论优势，先用经典Stackelberg博弈模型计算出先行造船企业的“先行优势”，再用完全信息离散分布的量子Stackelberg博弈模型来确定各种参数对“先行优势”的影响，以及“竞争情报”对整个量子Stackelberg博弈的重要作用。

竞争情报；量子Stackelberg博弈；最小化量子模型

Class NumberN941

1 引言

近三十年来中国船舶工业取得了巨大的成就，年造船吨位的世界排名由第十七位上升到前三位，许多高技术船舶的设计与制造技术都已基本掌握，大量先进设施的投入使用及对日韩造船技术的学习使生产效率大大提高。同时，大连新船重工、外高桥造船厂等现代化造船企业发展势头良好［1］。然而，根据迈克尔·波特的钻石体系理论［2］我国与国外先进造船国家之间仍存在着很大的差距。我国造船企业只有努力培养自己的核心竞争力，才能在激烈的竞争中掌握主动权［3］。在提高核心竞争力的同时，我国造船企业还要努力收集各种“竞争情报”以便在复杂的国际造船业竞争中能做出正确的决策，提高竞争力。

2 “竞争情报”的收集

竞争情报是对竞争环境、竞争形势的全方位研究。“竞争情报”不光是对竞争信息的收集，更是对竞争对手参与的竞争市场行为的研究。“竞争情报”的收集过程就是对整个竞争环境和竞争对手的全面监控的过程，其最终的目的就是竞争策略的选择。竞争企业能根据自己拥有的“竞争情报”，利用博弈的思想做出最有利于自己的决策。

对于我国造船企业来说，“竞争情报”收集的工作应该包含以下阶段，如表1所示。

表1 我国造船企业“竞争情报”收集工作阶段

随着“竞争情报”的收集，参与国际竞争的我国造船企业的信息结构和决策方式也随之改变。通过分析竞争对手和本国企业自身的情报需求、竞争环境，可以最终影响我国造船企业的竞争策略的选择，所以“竞争情报”作为一个关键的变量，在整个国际造船竞争中具有十分重要的作用。

3 量子博弈理论简介

量子博弈论是经典博弈理论和量子理论（特别是量子信息理论）结合后形成了一门新兴的交叉学科。1999年，J.Eisert等首次研究了囚徒困境的量子化模型［4］。分析表明，如果博弈双方采用量子策略，则可以解决经典博弈中的困境，处于最大纠缠态的量子博弈要明显优于经典博弈。随后，经典博弈中的许多模型被量子化，得到了不同于经典理论的奇妙结果，解决了许多经典博弈论无法解决的问题，如囚徒困境、PQ翻硬币问题等。除了理论研究之外，J.Du等首次用核磁共振量子计算机实现了囚徒困境这一量子博弈的全过程，并得到了与理论计算完全一致的结论［5］。

Stackelberg模型是博弈论中一个典型的动态博弈模型。在该模型中，产量决定产品的价格，且两个企业按照先后顺序选择各自的策略。C.F.Lo等采用最小化量子模型研究了完全信息离散分布的量子Stackelberg博弈。分析表明，相对于经典情况，正的量子纠缠增强先行优势，负的量子纠缠减弱先行优势。在信息离散分布的Stackelberg博弈模型中，先行企业的不确定信息将减弱的先行优势，但是，正的量子纠缠将增强先行企业对信息不确定度的容忍程度。

4 基于量子Stackelberg博弈理论的造船企业国际竞争模型

假设在国际造船市场上某国外企业（领头企业1）一直致力于某型船模的设计和制造（如LNG、VLCC及好望角型散货船）我国造船企业（尾随企业2）经过“竞争情报”收集与分析后决定生产该型船舶，于是市场竞争（博弈）就自然的发生了。

4.1 造船企业的完全信息经典Stackelberg博弈模型

Stackelberg模型讨论的是生产同种商品的两家企业选择产量，产品的价格由产量决定。利用该模型，领头造船企业1首先选择产量q1≥0。尾随造船企业2经过收集“竞争情报”观测到q1，然后选择自己的产量q2≥0。因此，这是一个完全信息动态博弈模型。这里，造船企业1和造船企业2的行动空间A1＝A2＝［0，＋∞）是连续空间。由于造船企业2选择行动q2依赖于q1，因此可表示为q2＝A2（q1）。收益函数应为μi＝μi（q1，q2）＝μi（q1，A2（q1）），i＝1，2。假定逆需求函数为P（Q）＝a－Q＝a－（q1＋q2）（这里Q＝q1＋q2表示总产量），两个企业有相同的不变单位成本c≥0。那么，造船企业1和造船企业2的利润函数分别为给出用“逆向归纳法”找出子博弈精炼纳什均衡的详细过程。首先分析在造船企业1选择q1的条件下，造船企业2选择产量q2的最优反应q2＝R2（q1）。

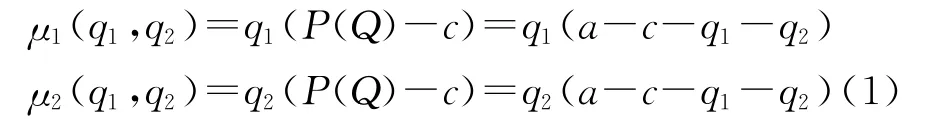
要使造船企业2的收益函数达到最优化，即

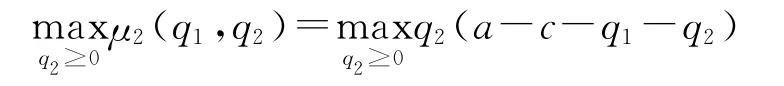
利用微积分求极值的方法，令收益函数μ2关于q2的一阶导数等于0，解出最优反应函数为

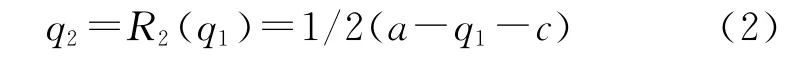
由于造船企业1知道造船企业2一定根据最优反应q2＝R2（q1）选择产量q2，则在决策的第一阶段，造船企业1的决策问题也就是求解最优化问题

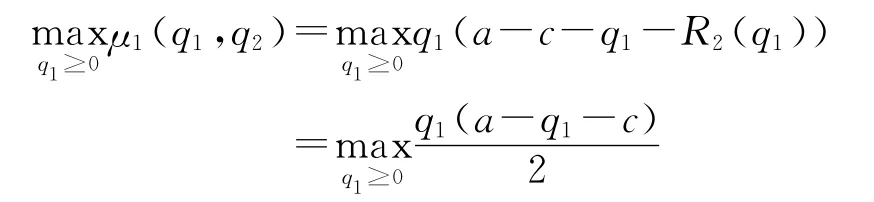
由收益函数μ1关于q1的一阶导数等于0，可解得

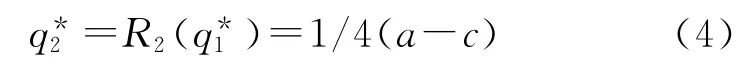
这就是该模型的子博弈精炼纳什均衡结果，也称为Stackelberg均衡结果。两个造船企业的利润分别为

4.2 造船企业的完全信息离散分布的量子Stackelberg博弈模型

2002年，H.Li等首次建立了“最小化量子模型”［6］，如图1所示。

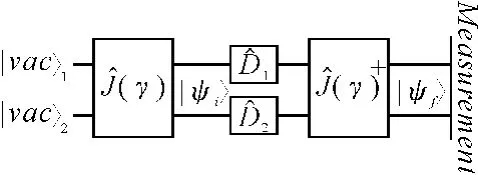
图1 最小化量子模型

2003年，C.F.Lo等首次采用最小化量子模型研究了完全信息的量子Stackelberg博弈模型［7］。利用该模型，把两个造船企业实际产量

代入利润函数表达式（1），可得两个造船企业的利润函数分别为

由逆向归纳法可得该量子博弈模型的最优解：

令k＝a－c，计算可得各个造船企业的利润和先行优势分别为

由式（8）可知，当γ≥0时，先行优势δ＊q关于γ单调递增；当γ＜0时，先行优势δ＊q关于γ单调递减；当γ＝0时，该模型即为经典博弈模型。所以，相对于经典情况，正的量子纠缠将增强先行优势，负的量子纠缠将减弱先行优势。

4.3 造船企业的不完全信息离散分布的量子Stackelberg博弈模型（竞争情报在博弈中的作用）

2005年，C.F.Lo等采用最小化量子模型研究了不完全信息离散分布的量子Stackelberg博弈模型［8］。其中，造船企业1由于没有“竞争情报”收集不完全，所以并不知道造船企业2的产品成本c2，只知道c2等于高成本c2H和低成本c2L的概率分别为θ和1－θ。由海萨尼转换，可得造船企业1和造船企业2的利润函数分别为

同样的，采用最小化量子模型，并把测量结果代入利润函数式（9），可得：

由逆向归纳法可得该量子博弈模型的最优解，代入可得各个造船企业的利润和先行优势分别为

由式（11）可知，领头造船企业要想保持先行优势，自变量ξ必须满足：

自变量ξcq表示先行造船企业在保持先行优势时对信息不确定度的容忍程度。ξcq关于量子纠缠度γ单调递增，当γ＝0时取得最小值1／4，当γ→∞时ξcq趋近于最大值4／9。换言之，正的量子纠缠将增强先行造船企业对信息不确定度的容忍程度。

5 结语

通过上文论述，在参与竞争的造船企业都是理性的前提下，可以得到如下结论：

1）领头造船企业的先行优势是客观存在的。由经典Stackelberg博弈模型可知领头造船企业的利润大于尾随造船企业的利润，这是领头造船企业首先行动（先进入市场）的结果。

2）领头造船企业的先行优势不是一成不变的。由完全信息离散分布的量子Stackelberg博弈模型知道，正的量子纠缠将增强领头造船企业的先行优势，负的量子纠缠将减弱先行优势。

3）打破领头造船企业的先行优势的关键就是努力收集竞争对手的“竞争情报”并保护自己的“信息”不被竞争对手知道。由不完全信息离散分布的量子Stackelberg博弈模型可以看到，领头造船企业的先行优势关于“信息的不确定度”单调递减，即领头造船企业对信息的不确定将会减弱它的先行优势。

4）如果我国造船企业变成“领头企业”，该如何保住先行优势。努力收集竞争对手的“竞争情报”并保护自己的“信息”不被竞争对手知道是保住先行优势的关键。若用ξcq表示先行造船企业在保持先行优势时对信息不确定度的容忍程度。ξcq关于量子纠缠度γ单调递增，当γ＝0时取得最小值1／4，当γ→∞时ξcq趋近于最大值4／9。换言之，正的量子纠缠将增强先行造船企业对信息不确定度的容忍程度。

5）市场的竞争就是“情报”的竞争、“信息”的竞争。无论是领头企业还是尾随企业为了获取最大的利益，都应该把收集“竞争情报”放在重要的地位。

［1］长塚诚治.中国造船技术的实力［J］.海外海事情报，2002（8）：1－5.

［2］迈克尔 波特.国家竞争优势［M］.北京：华夏出版社，2003.

［3］陈强.论中国造船企业的核心竞争力［J］.中国造船，2004，45（1）：1－6.

［4］J.Eisert，M.Wilkens.Quantum games［J］.J.Modern Opt.，2000，47：2543.

［5］R.Raussendorf，D.E.Browne，H.J.Briegel.Measurement－based quantum computation with cluster states［J］.Phys.Rev.A，2003，68：022312.

［6］H.Li，J.F.Du，S.Massar.Continuous－variable quantum games［J］.Phys.Lett.A，2002，306：73.

［7］C.F.Lo，D.Kiang.Quantum Stackelberg duopoly［J］.Phys.Lett.A，2003，318：333.

［8］C.F.Lo，D.Kiang.Quantum Stackelberg duopoly with incomplete information［J］.Phys.Lett.A，2005，346：65.

China ShipbuildingEnterprises Quantum StackelbergDuopolyand the International Competition

YANG Ji1FENG Weidong2FENG Yingying3WANG Xia1
（1.Mathematical Modeling Lab，Huazhong University of Science and Technology Wenhua College，Wuhan 430074）（2.Wuhan Digital Engineering Institute，Wuhan 430205）（3.Wuhan Vocational College of Communications and Publishing，Wuhan 430223）

Over the past three decades，China's shipbuilding industry has made great achievements.The world ranking of anuual shipbuilding tonnage has risen to the top three from the previous seventeenth，numerous advanced facilities has been put into use，learning shipbuilding technology from Japanese and Korean has greatly improved the production efficiency.So，the strtegic objectives of China's shipbuilding enterprises，we struggle to achieve over the next decade，lie in keeping our status as the shipbuilding power in the world and moving realistically from shipbuilding country towards shipbuilding power.At the same time of improving core competitiveness，China's shipbuilding enterprises must strive to collect various"Competitive intelligence"，so as to make the right decisions in the complex international shipbuilding situation，and to improve international competitiveness as well.Combining the theoretical advantages of Stackelberg game，this article firstly calculates out the"first advantage"of the first shipbuilding enterprises with classic model of Stackelberg game，then with the quantum Stackelberg game model of complete information descrete distributions，the influence of various parameters on the"first advantage"，as well as the important role of"competitive intelligence"in the whole Stackerberg game can be defined.

competitive intelligence，quantum stackelberg duopoly，minimize quantum model

N941DOI：10.3969／j.issn.1672－9730.2015.11.003

2015年5月8日，

2015年6月25日

杨戟，男，硕士，讲师，研究方向：量子运筹学、数量情报与数学模型。