基于最佳一致逼近法的逆海洋滤波器设计＊

马平原

（92349部队 淄博 255178）

基于最佳一致逼近法的逆海洋滤波器设计＊

马平原

（92349部队 淄博 255178）

针对海水低通特性会使水下超低频段大气噪声波形畸变，使接收超低频信号时信噪比变差的问题，研究了海水在超低频段的幅频特性，仿真了在不同深度上海水对超低频大气噪声的影响，并采用最佳一致逼近法设计了逆海洋滤波器，对畸变的大气噪声波形进行频率补偿。当采样率fs＝1kHz时，在30m～200m深度上最大采用9阶IIR滤波器，可以使逆海洋滤波器的幅频特性与理论值的最大偏差小于0.5dB，能够很好的还原超低频大气噪声尖峰的锐利程度，提高了接收信号的信噪比。

大气噪声；最佳一致逼近法；逆海洋滤波器

Class NumberTP274

1 引言

在超低频通信中，超低频大气噪声能够和信号一起穿透海水到达接收设备，严重影响超低通信的质量，所以对超低频大气噪声的研究和处理是超低频通信中极为重要的一部分。文献［1～4］对超低频大气噪声进行了权威的记录，研究了其统计特性；文献［5～11］对大气噪声进行了建模和参数估计，对大气噪声的非线性处理方法提供了指导。以上研究的大气噪声都是在水面以上，但是，由于海水在超低频段对信号的幅频响应呈现明显的低通特性，海面下超低频段大气噪声的特性会发生明显的变化。无论是采用线性和非线性的处理方式，其特性的变化都会使接收过程中残留的噪声功率变大或者参数估计偏差而导致信噪比变差，这对于要求在接收端尽量提高信噪比，从而节省发端系统代价的超低频通信是相当不利的。所以，在进行线性或者非线性处理之前，需要通过逆海洋滤波器还原大气噪声的特性。

2 海水在超低频段的幅频特性

电磁波在海平面传播的过程中，设其垂直电场分量为Ev，水平磁场分量为Hh，Ev＝η0Hh，η0为自由空间波阻抗。水平磁场分量Hh在海平面上感应产生的二次场是一个径向水平电场分量Eh，Eh就是由大气层进入海水并向海水深处传播的主要电场分量。Ev和Eh比值的关系如式（1）。其中，λ0为电磁波在自由空间的波长，σ为海水的电导率。

设z为海水深度，z＝0为海面，由大气进入海水的水平电场分量表示为Eh（0），其向下传播的水平电场分量可用式（2）表示。其中，Eh（z）为深度为z处的水平电场分量为衰减常数为相移常数。

海水中深度z处的水平电场分量与海水表面的水平磁场分量之间的关系如式（3）。

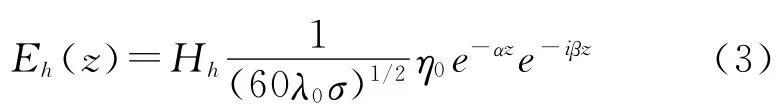
所以海水的低通特性由传递函数（4）给出。

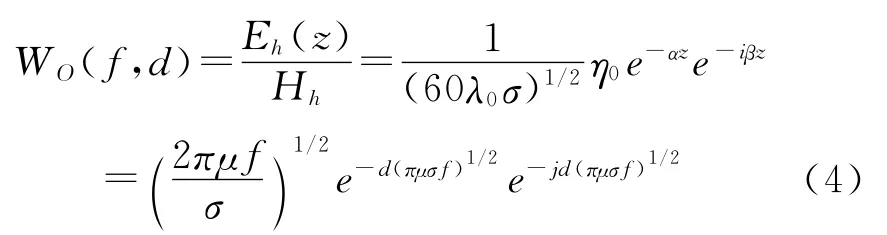
由式（4）可以得出，海水的低通特性是海水的深度z、信号的频率f和海水的电导率σ的函数。假设取海水的电导率σ＝4.0（S／m）为常数时，得到海水在超低频段的幅频特性曲线；以一定的间隔取不同的海水深度，可以在平面上得到相频特性曲线，如图1所示。

图1 海水的幅频特性曲线

由图1可见，假设海水电导率为常数，当深度大于30m时，海水对超低频段信号的幅频响应呈现出低通特性，随着深度的增加，低通特性越明显。

3 海水低通特性对超低频大气噪声的影响

大气噪声引起的天电干扰产生的，它可以以很低的衰减率传播数千公里并且穿透海水，和超低频信号一起到达海水中的接收设备，对接收性能产生严重的影响。超低频大气噪声具有明显的非高斯特性，其可以看成是在高斯噪声背景下叠加了大量的尖峰脉冲，图2所示为记录的时长为1s的典型的超低频大气噪声时域波形。

图2 海面上时长为1s的超低频大气噪声波形

图3 海水50m深度下超低频大气噪声波形

图4 海水50m深度下超低频大气噪声波形

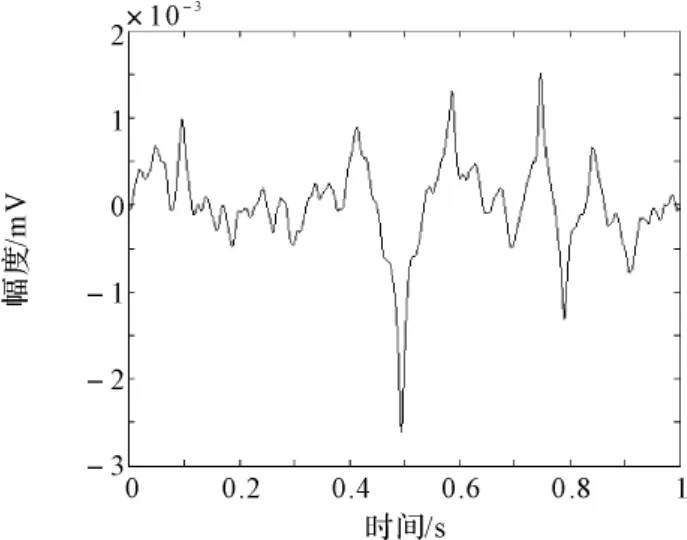
图5 海水180m深度下超低频大气噪声波形

由于现有的收信设备都是采用线性接收方式，对于超低频大气噪声的处理一般都是采用削波器或熄灭器的方式，这样可以除去噪声中尖峰脉冲的大部分功率，从而提高了信噪比。非线性的处理方式是通过对大气噪声的建模和参数估计，设计相应的匹配滤波器来消除大气噪声的影响。

由于海水的低通特性，超低频噪声在传入到水下越深的深度时，其尖峰脉冲的特性会改变，使其在时域上的波形会变宽，尖锐程度锐减，图3～图5分别为上述超低频大气噪声在水下50m、100m和180m的深度上时域的波形。可以看出，随着深度的增加，噪声中的尖峰脉冲的波形会变得越宽，以致在采用线性方式对其进行处理时，信号中留下的噪声功率将大幅度增加；采用非线性的方式进行处理时，由于大气噪声的特性发生变化，致使通过参数估计设计的匹配滤波器的参数有偏差，都会使得信噪比变差。对于超低频通信中传输的带宽相对较小的有用超低频信号来说，这种影响是可以忽略的，但对于噪声特性的影响是十分明显的。

4 逆海洋滤波器的设计

逆海洋滤波器，就是通过对频率特性进行补偿，把海水低通特性补偿平衡，其幅频特性应与海水的低通特性完全相反。逆海洋滤波器的幅频响应如式（5）所示，设海水的电导率σ＝4.0（s／m）为常数时，得到以深度为参数的幅频响应曲线如图6所示。

图6 逆海洋滤波器的幅频特性曲线（σ为常数）

在接收设备对接收到的信号进行放大、采样以后，由数字滤波器的形式实现逆海洋滤波器。由于海水对信号产生的相位变化在超低频段近似是线性的，所以逆海洋滤波器采用具有线性相位的FIR滤波器，这样对于信号的相位变化在后级可由延迟均衡器来进行补偿。

设计逆海洋滤波器时，其幅频响应与海水低通特性的近似可由插值法、最小平方逼近法和最佳一致逼近法来实现。各方法的区别在于对误差函数E（ω）＝H（ω）－WIO（ω），即近似幅频响应H（ω）与理论幅频响应WIO（ω）的差值要求不同。由于超低频噪声频谱特性呈现在超低频段的整个频段内，所以采用使误差函数E（ω）均匀一致，并且能够使E（ω）的最大值达到最小的最佳一致逼近法来进行设计。最佳一致逼近法遵循的是最大误差最小化的设计准则，其算法为McClellan－Parks－Rabiner算法［12］，采用Matlab编程实现其算法，算法流程图如图7所示。其中E（ωk）为在各频点ωk处的权重系数，因为在接收信号过程中，都会对超低频信号进行带通滤波，所以噪声也会通过f＝20Hz～200Hz的带通滤波器，所以W（ωk）在f＝20Hz～200Hz所对应的ωk处权重取1，也即是要求逆海洋滤波器在f＝20Hz～200Hz与理论的幅频响应一致。

图7 最佳一致逼近法设计逆海洋滤波器程序流程图

超低频段的信号在针对每一个深度，可以得出相对应的逆海洋滤波器的系数。当采样率fs＝1kHz时，为了使误差小于0.5dB，在深度为30m～70m时，采用3阶FIR滤波器；80m～150m时，采用7阶FIR滤波器；160m～200m时，采用9阶FIR滤波器即可实现。图8所示为在z＝180m深度上，所设计的9阶FIR滤波器的幅频特性，在f＝20Hz～200Hz频段上与理论值的误差为0.09dB。表1列出了在部分深度上设计的滤波器的传递函数。当采样率增大时，则应当增大滤波器的阶数来满足误差的范围。在z＝180m深度上经过逆海洋滤波器还原的信号如图9所示，基本上恢复了噪声信号中尖峰的锐利程度，从而在后级处理过程中提高信噪比。

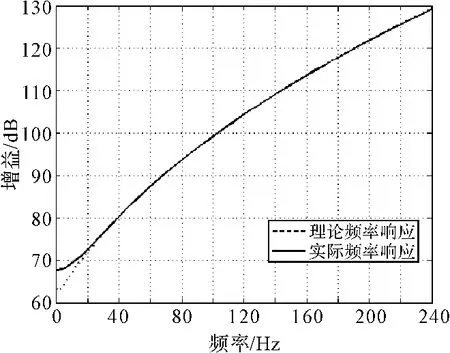
图8 深度180m下逆海洋滤波器幅频特性曲线和理论幅频特性曲线

图9 经逆海洋滤波器恢复后的超低频大气噪声波形

表1 不同深度下逆海洋滤波器的传递函数

5 结语

海水在超低频段的幅频响应呈现低通特性，并随着深度的增加低通特性越明显，相频响应近似线性；这种低通特性会使穿入水下的超低频大气噪声尖峰的锐利程度变差，无论是采用线性和非线性的处理方式，其特性的变化都会导致信噪比变差。根据海水幅频响应和相频响应的性质，采用基于最佳一致逼近法的McClellan－Parks－Rabiner算法设计实现了逆海洋滤波器，对畸变的大气噪声波形进行频率补偿。当采样率fs＝1kHz时，在30m～200m的深度上最大采用9阶IIR滤波器，可以使设计的逆海洋滤波器和理论逆海洋滤波器幅频特性的最大偏差小于0.5dB，能够很好地还原超低频大气噪声尖峰的锐利程度，提高了接收信号的信噪比。

［1］ITU－R P.Radio Noise［S］.Grneva Switzerland：International Telecommunication，2009.

［2］Chrissan D A.Statistial Analysis and Modeling of Low－Frequency Radio Noise and Improvement of Low－Frequency Communications［R］.Stanford：Stanford University，1999.

［3］Chrissan D A，Fraser－Smith A C.Diurnal Variations of Globally measured ELF／VLF Radio Noise［R］.Stanford：Stanford University，1997.

［4］Chrissan D A，Fraser－Smith A C.Seasoal Variations of Globally measured ELF／VLF Radio Noise［R］.Stanford：Stanford University，1997.

［5］付天晖，周穗华，王永斌.超低频遥控系统的噪声建模与抑制［J］.电波科学学报，2011，26（2）：332－338.

［6］Tianhui Fu，Suihua Zhou，Xiaobing Zhang.Detection for Signal in ELF Atmospheric Noise Interference［C］／／2010 2nd IEEE International Conference on Information Management and Engineering（ICIME），2010：409－412.

［7］梁高权.甚低频波和超低频波的辐射和传播［M］.南京：海军电子工程学院，2002：262－264.

［8］蒋宇中.超低频信道统计特性及应用［D］.武汉：华中科技大学，2008：21－27.

［9］Hall H M.A New Model for“Impulsive”Noise Phenomena：Applications to Atmospheric Noise Channels［D］.Stanford：Stanford University，1966：3－11.

［10］Nikias C L，Shao M.Signal Processing with Alpha－Stable Distributions and Amplications［M］.New York：John Wiley ＆Sons，1995：1－45.

［11］张曙霞，徐大勇，蒋宇中.超低频大气噪声幅度概率分布模式的辨识［J］.应用科学学报，2008，26（4）：336－341.

［12］胡广书.数字信号处理［M］.北京：清华大学出版社，2003：313－321.

Research on Ocean－compensation Filter Based on Best Uniform Approximation Method

MA Pingyuan
（No.92349Troops of PLA，Zibo 255178）

The low－pass characteristic of the ocean in ELF band will result in distortion of the atmospheric noise and worse signal to noise of the receiver.To address this problem，magnitude－frequency characteristic of the ocean in ELF band were researched.Influence on the atmospheric noise in different depth of the ocean was simulated.And ocean－compensation filter was designed using best uniform approximation method to compensate the distorted atmospheric noise.With the sampling frequency fs＝1kHz，at 30m～200mdepth，9th－order IIR filter was used to design ocean－compensation filter.The maximal error of the magnitude－frequency characteristic of the filter is less than 0.5dB compared with the theoretical.With the filter，the sharpness of the ELF atmospheric noise spikes were restored and the SNR of the receiver was improved.

atmospheric noise，best uniform approximation method，ocean－compensation filter

TP274DOI：10.3969／j.issn.1672－9730.2015.11.046

2015年5月14日，

2015年6月23日

马平原，男，工程师，研究方向：军用目标特性及信息处理。