配电网谐波分析的傅里叶变换方法

沈 杰，孟晓芳，王英男，侯 森，张 帆，赵夕彤

（1.国家知识产权局专利局专利审查协作北京中心，北京 100096；2.沈阳农业大学，辽宁 沈阳 110866；3.国网沈阳供电公司，辽宁 沈阳 110003）

配电网谐波分析的傅里叶变换方法

沈 杰1，孟晓芳2，王英男3，侯 森2，张 帆2，赵夕彤2

（1.国家知识产权局专利局专利审查协作北京中心，北京 100096；2.沈阳农业大学，辽宁 沈阳 110866；3.国网沈阳供电公司，辽宁 沈阳 110003）

随着国民经济和电力工业的发展，配电网中的谐波不断增加，有效的、易于工程使用的谐波分析方法十分重要。在电力网的谐波分析中，傅里叶变换方法是从信号中提取基波分量和谐波分量的最常用方法。介绍了分析谐波的傅里叶变换方法，给出了数学模型，并且利用Matlab进行了仿真分析。通过仿真分析可见，傅里叶变换方法在谐波分析方面，具有计算简单和易于工程实现的特点，而且能够反映整个信号的频谱，可以很直观地得到配电网各次稳态谐波的幅值。

傅里叶变换；配电网；谐波分析；仿真

随着国民经济和电力工业的发展，电力系统非线性负荷的日益增多［1］，电力电子装置的广泛应用［2－4］，高压直流输电、柔性交流输电和客户电力技术的不断进入工程应用［5］，风电场的接入［6］，电气化铁路对供电系统的影响［7］及电力系统故障［8］等，电网产生了大量的高次谐波，电力系统中的谐波不断增加。谐波“污染”问题日益严重，威胁电力设备的安全运行，对谐波的分析和研究受到广泛关注［9］。为了构建绿色电网，及时解决电网谐波治理难题，达到准确分清谐波责任且简单有效的治理目的，必须先明确电力系统中的谐波分布或谐波状态。

对谐波含量进行准确分析，掌握电网中谐波的实际状况，对于防止谐波危害、维护电网安全经济运行十分必要。以傅里叶变换为基础的加算法是电力系统谐波分析普遍采用的一类算法。傅里叶变换是常用的电力谐波分析方法，具有计算简单和易于工程实现的特点。

本文主要是利用傅里叶变换，基于Matlab仿真，进行电力谐波分析。

1 傅里叶变换原理

1.1 傅里叶变换简介

傅里叶变换法作为传统方法，是时域和频域相互转化的工具，它是谐波分析中最基本的算法。傅里叶变换的实质是把对原函数f（t）的研究转化为对其傅里叶变换f（ω）的研究。

傅里叶变换法能够将信号的时域特征与频域特征联系起来，有很高的频率分辨能力。

对电力系统中周期性的非正弦电量进行傅里叶级数分解，可以得到频率大于电网基波频率的分量，其中，基波频率整数倍的分量称之为谐波。计算周期性波形中的基波与高次谐波的幅值和相位，即为谐波分析。进行谐波分析的思想是利用傅里叶变换将畸变波形分解成基频分量和各次谐波分量，通过频谱分析各次谐波分量的幅值和相位来描述波形畸变水平［10］。随着频谱理论的发展，傅里叶变换在谐波分析中的应用也越来越广泛。频谱分析中常使用能反映频率与振幅关系的频谱图。采用傅里叶变换时必须满足两个条件：最高信号频率小于采样频率的1／2，且被分析信号是稳态的。

1.2 傅里叶变换的数学理论

设f（t）是以2π为周期的函数，且在［－π，π］或［0，2π］上可积，则函数f（t）的傅里叶系数如下：

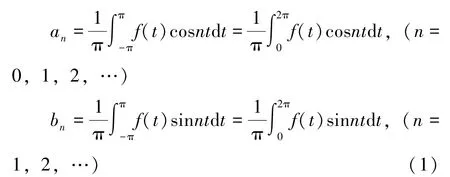
以f（t）的傅里叶系数为系数的三角级数，即函数f（t）的傅里叶级数形式如下：

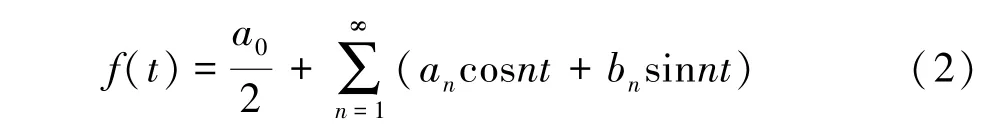
设f（t）是以2T为周期的函数，且在［－T，T］上可积，则其傅里叶系数为

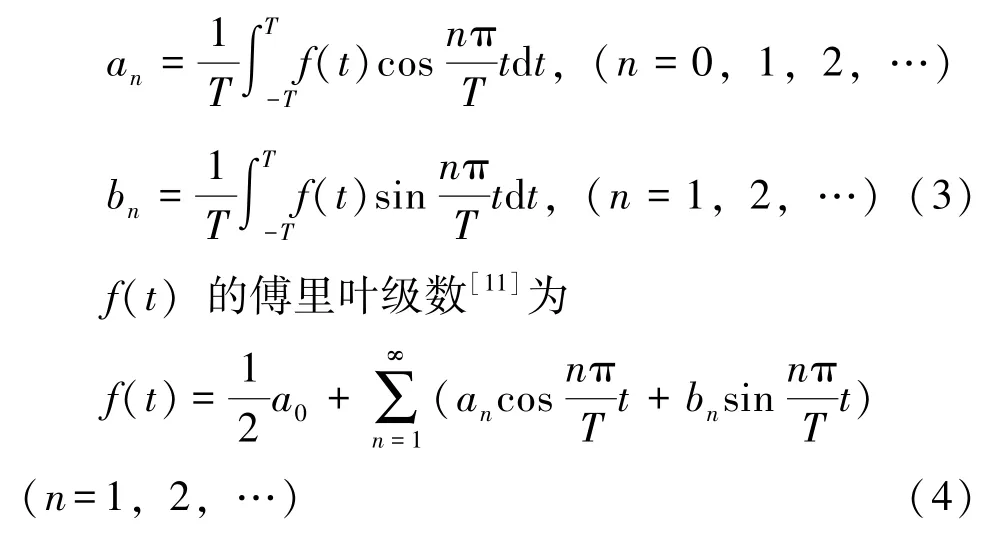
2 谐波分析

对于以T为周期的周期函数fT（t），如果fT（t）满足狄利赫利条件，fT（t）可以展开为一个收敛的傅里叶级数：

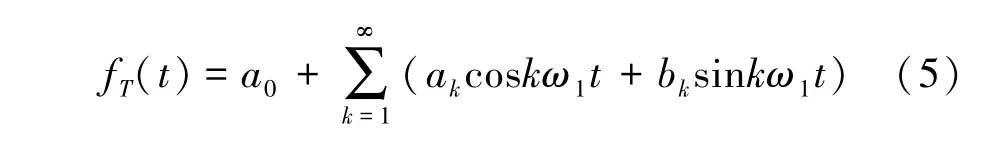
式中：k＝1，2，3，…；ω1为基波角频率。

fT（t）的第k次谐波为

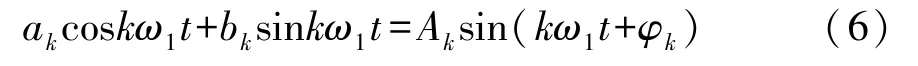
式中：Ak为第k次谐波的振幅，

而在复指数形式中，第k次谐波为

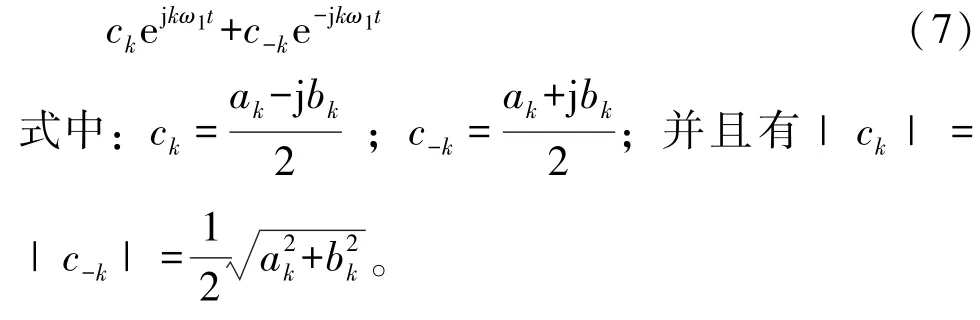
所以，以T为周期的非正弦函数fT（t）的第k次谐波的振幅为

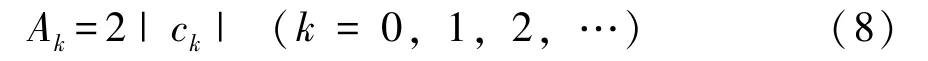
上式可以描述各次谐波的振幅随频率变化的分布情况。用长度与各次谐波振幅大小相对应的线段，按频率的高低顺序把他们依次排列起来就可以得到fT（t）频谱图。这种频谱只表示各次谐波分量的振幅，为fT（t）的振幅频谱，简称频谱。由于k＝0，1，2，…，所以振幅频谱的图形不是连续的，是离散频谱［12］。

频谱图能清楚地表明一个非正弦周期函数包含了哪些频率的谐波分量及各分量所占的比重，这样就可以求出谐波畸变率。畸变率或正弦波形畸变率是指各次谐波有效值平方和的方根值与基波有效值的百分比［13］。

3 仿真分析

为了应用傅里叶变换进行电力谐波分析，基于Matlab构建了仿真系统，如图1所示，系统的输入波形如图2所示。利用Matlab实现谐波分量的分解。

用模块Powergui中的FFT analysis按钮使用FFT tools对话框可以显示输入谐波波形和波形中各次谐波所占的比例条形图，如图3所示。

从图3中可以看出，波形畸变率THD为11.22%，输入波形包括：直流信号、基波、3次谐波、4次谐波、10次谐波。

以基波（50 Hz）为基准，各次谐波所占的百分比如图4所示。

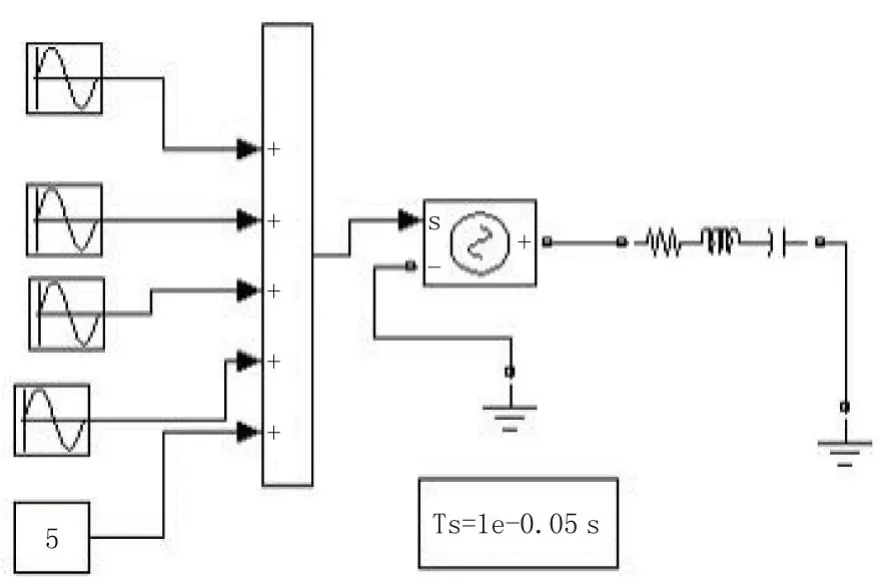
图1 仿真系统

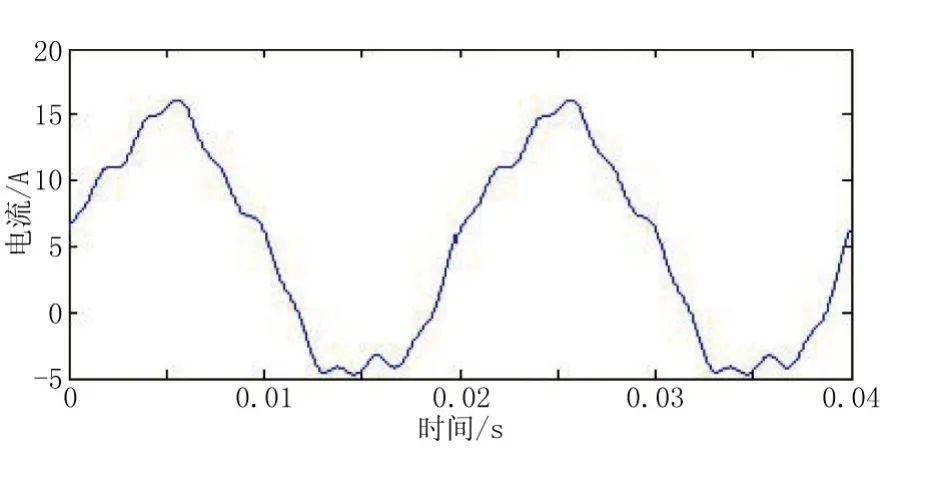
图2 输入波形

图3 各次谐波所占基波的比例图

图4 各次谐波所占基波的百分比

4 结束语

配电网的谐波分析是配电网谐波治理的前提。对谐波含量进行准确分析，确切掌握电网中谐波的实际状况，对于防止谐波危害、维护电网安全经济运行十分必要。针对谐波分析的问题，本文探讨了谐波分析的傅里叶变换方法，并且利用Matlab进行了仿真分析，通过仿真分析可以看出，傅里叶变换方法在谐波分析方面，能够反映整个信号的频谱，可以很直观地得到各次谐波的幅值，具有计算简单和易于工程实现的特点，在谐波分析方面有显著的优势。

今后可以进一步分析傅里叶变换在电压偏差计算、不对称故障电流方面的应用。

［1］ 何珊珊.电能计量中谐波对计量结果的影响及防范［J］.中国电力教育，2013，29（11）：195－196.

［2］ 陈国志，陈隆道，蔡忠法.基于Nuttall窗插值FFT的谐波分析方法［J］.电力自动化设备，2011，31（4）：27－31.

［3］ 蔡晓峰，张鸿博，鲁改凤.应用三谱线插值FFT分析电力谐波的改进算法［J］.电力系统保护与控制，2015，43（2）：33－39.

［4］ 龚 静.小波变换与傅立叶变换在谐波分析中应用比较［J］.东北电力技术，2009，30（9）：21－24，39.

［5］ 梁志瑞，叶慧强，赵 飞.电力系统谐波状态估计研究综述［J］.电力系统保护与控制，2010，38（15）：157－160.

［6］ 蔡志远，戈阳阳，马少华.大规模风电接入电网谐波影响研究［J］.东北电力技术，2014，35（4）：31－34.

［7］ 商文颖，梁 毅，凌立平.电气化铁路对沿线电力系统电能质量的影响研究［J］.东北电力技术，2011，32（9）：8－10，30.

［8］ 邱关源.电路［M］.北京：高等教育出版社，2004.

［9］ 李天云，张方彦，贺建伟.谐波小波变换在电力系统谐波检测中的应用［J］.东北电力技术，2008，29（4）：5－8.

［10］ Makoto Saito，Takaharu Takeshita，Nobuyuki Matsui.Modeling and Harmonic Suppression for Power Distribution Systems［J］. IEEE Transactions on Industrial Electronics，2003，50（6），1 148－1 158.

［11］ 同济大学应用数学系.高等数学（下册）［M］.北京：高等教育出版社，2002.

［12］ 张元林.工程数学.积分变换［M］.北京：高等教育出版社，2003.

［13］ 陈 衍.电力系统稳态分析［M］.北京：中国电力出版社，2007.

Fourier Transform Method for the Harmonic Analysis in the Power Distribution Network

SHEN Jie1，MENG Xiao⁃fang2，WANG Ying⁃nan3，HOU Sen2，ZHANG Fan2，ZHAO Xi⁃tong2
（1.Patent Examination Cooperation Center of the Patent Office，SIPO，Beijing 100096，China；2.Shenyang Agricultural University，Shenyang，Liaoning 110866，China；3.State Grid Shenyang Power Supply Company，Shenyang，Liaoning 110003，China）

With the development of national economy and power industry，the harmonic in the distribution network is increasing，so an effective and easy method of harmonic analysis is very important.In the power grid harmonic analysis，the Fourier transform is the most common method to extract the fundamental wave and the harmonic components from the signal.This paper introduces the Fourier transform method for the harmonic analysis，and its mathematical model is given.In the MATLAB platform，the corresponding simula⁃tion analysis are presented.Through the simulation analysis，it is showed that the Fourier transform is simple to calculate and realize in engineering.The whole spectrum of signal can be reflected，and it is very intuitive to get the each steady state harmonic amplitude in the distribution network.

Fourier transform；Distribution network；Harmonic analysis；Simulation

TM935

A

1004－7913（2015）10－0021－03

国家科技支撑计划课题（2012BAJ26B00）；辽宁省自然科学基金项目（201202191）；国家科技支撑计划子课题（2012BAJ26B01⁃6）

沈 杰（1979—），女，硕士，助理研究员，主要研究方向为电力系统电能质量分析和新能源发电。

2015－07－10）