EKF-SLAM算法的改进及其在Turtlebot的实现

薛永胜 王 姮 张 华 霍建文

(西南科技大学特殊环境机器人技术四川省重点实验室 四川绵阳 621010)



EKF-SLAM算法的改进及其在Turtlebot的实现

薛永胜 王 姮 张 华 霍建文

(西南科技大学特殊环境机器人技术四川省重点实验室 四川绵阳 621010)

针对标准扩展卡尔曼滤波(EKF)在移动机器人同时定位与地图构建(SLAM)过程中计算量大、实时性差、精度低、易受干扰等问题，结合平滑算法和奇异值分解运算，提出了一种基于EKF-SLAM算法的改进ERTSS-SLAM算法。改进ERTSS-SLAM算法使用前向EKF滤波对移动机器人里程计和陀螺仪的位姿信息进行最优估计，再使用标准ERTS平滑器进行后向递推避免发散，同时使用奇异值分解法避免标准EKF滤波产生的求逆运算，有效提高了系统实时性，增强了系统的鲁棒性和定位精度。Turtlebot移动机器人的实验效果证明了该算法在SLAM应用中的高效性和稳定性。

同时定位与地图构建 平滑算法 奇异值分解 Turtlebot

伴随工业4.0概念的提出和世界范围内机器人技术的蓬勃发展，智能机器人的同时定位与地图构建(simultaneous localization and mapping，SLAM)问题已成为移动机器人领域备受关注的研究方向[1-2]，也是移动机器人智能化发展的重要支撑。

目前，解决SLAM问题中的EKF-SLAM，PF-SLAM，FastSLAM及UKF-SLAM等经典算法[3]中，EKF-SLAM算法最先被提出、最为流行。但EKF中的非线性对象线性化过程引入了较大误差，且雅克比矩阵计算较复杂，使得其精度和实时性难以满足实际应用需求。针对EKF的缺点，Gurkan Tuna[4]等人通过对标准EKF、压缩卡尔曼滤波(CEKF)、无迹卡尔曼滤波(UKF)3种算法占用的计算资源和耗时进行测评，发现CEKF更适合室外SLAM的应用，并对CEFKF的应用进行了仿真实验，证明了其有效性；Andrea Griffo[5]等人在EKF-SLAM的基础上提出双EKF滤波的传感器解决方法，一个EKF用于路径预测，一个用于路标预测，提高了精度，但是计算复杂；张毅[6]等提出了修正迭代扩展卡尔曼滤波算法(MIEKF)，降低了对系统传感器精度的依赖度，减小了线性化误差。Wang Daobin[7]等人通过对不同移动机器人的动态模型改进，提出了一种适用于多种移动机器人平台的改进EKF-SLAM算法，降低了计算复杂度，提高了精度。杜航原[8]等提出了一种改进的模糊自适应卡尔曼滤波算法，改变系统对观测信息的依赖和利用程度，使滤波器最终趋于稳定，保证了实时性和精度。

现有的多种对EKF-SLAM算法的改进在一定程度上可以单独改善实时性或者精确度，但无法同时保证其鲁棒性和计算效率，因此难以满足实际应用需求。为解决这些问题，本文提出一种基于EKF-SLAM的改进ERTSS-SLAM算法。

1 EKF-SLAM算法

移动机器人的自定位过程是一个非线性化的过程，从统计的角度看，SLAM问题是一个滤波问题，在系统噪声和测量噪声服从正态分布的情况下EKF可以很好地去除系统中的噪声干扰实现最优估计，因此Smith和Cheeseman提出使用EKF来估计 SLAM问题的EKF-SLAM算法，该算法流程框图如图1。

图1 EKF-SLAM算法流程Fig.1 EKF-SLAM algorithm flow

1.1 EKF原理

扩展卡尔曼滤波算法是一种常用的非线性滤波方法，其原理是在预测点xk|k-1将系统状态方程和测量方程进行泰勒展开，并忽略所有非线性展开高阶项来实现对非线性方程的线性化近似[9]。常用的非线性离散随机系统模型如下：

xk+1=f(xk,uk)+w(t)

(1)

zk=h(xk)+v(t)

(2)

其中ω，v代表了附加在非线性系统运行过程中的0均值高斯噪声。将系统方程进行线性化表示为：

(3)

(4)

(5)

通过式(6)-式(8)迭代运算可进行预测更新，通过式(9)-式(12)迭代运算可进行状态更新。

xk+1|k=f(xk|k,uk)

(6)

Pk+1|k=JPk|kJT+Qk

(7)

(8)

(9)

ϑk+1=zk+1-h(xk+1|k)

(10)

xk+1|k+1=xk+1|k+Wk+1ϑk+1

(11)

(12)

1.2 EKF-SLAM算法

基于EKF的SLAM算法包含运动更新和观测更新两个过程，这两个过程分别是对系统的运动模型和观测模型的描述[10]。运动更新过程是用各传感器数据作为输入控制量，对机器人当前位置进行预测估计。观测更新是当移动机器人观测到当前环境中的特征点并与局部地图匹配，同时更新机器人在地图中的位置的过程。通常机器人SLAM将位姿信息xv和地图特征mi(xi,yi)存储在一个独立的状态向量xml中：

(13)

(14)

整个地图信息为MB=(xml,Pml)。

EKF-SLAM具有定义明确、算法编程实现容易等特点，最大的缺陷就是假设系统中的各种不确定性参数符合高斯分布，这在严重情况下，会造成数据关联的不准确，从而导致算法发散。而且，随着环境特征点个数的增加还会造成输出协方差阵中的元素以平方倍数成倍增加，导致运算量增加[11]。

2 改进ERTSS-SLAM算法

2.1 ERTSS-SLAM算法

ERTS平滑算法能对某一时间区间内的所有量测信息和状态进行估计的离线处理，能够获得优于滤波的估计精度，广泛应用于声音信号处理、目标跟踪和导航制导等领域[12]，其原理框图如图2所示。图中上标“+”和“-”分别表示滤波的更新过程和预测过程，“F”和“S”分别表示前向滤波过程和后向递推平滑过程。

图2 ERTS平滑算法原理图Fig.2 ERTS smoothing algorithm schematics

前向EKF滤波过程利用固定时间区间[0N]内所有采样值进行，并存储式(6)-式(12)中的状态估计xk+1|k+1、后验估计协方差误差阵Pk+1|k+1和先验估计协方差误差阵Pk+1|k。其后向递推公式[13]如下：

(15)

(16)

其中后向递推的平滑增益矩阵：

(17)

ERTSS-SLAM算法具有EKF的优点，能够在线递推定位和建图，同时也能够离线估计进行定位和建图，避免估计的突变，但计算中协方差阵中的元素随着环境特征点数量呈指数增长，下文提出了相应的改进算法。

2.2 算法改进

ERTS平滑算法中存在大量n×n矩阵相乘，为简少运算过程的存储和计算量，采用奇异值分解法[14]对Ps,k和Ps,k+1进行定义得：

(18)

(19)

定义Mk满足：

(20)

将上式带入式(16)化简为：

(21)

为进行奇异值分解运算，求Mk的逆得：

(22)

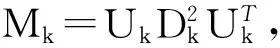
(23)

对上式两边分别左乘各自转置阵后得到：

(24)

由式(21)和式(23)得到：

(25)

同理可实现式(18)的奇异值分解运算得到：

(26)

将式(24)和式(25)带入式(16)和式(17)可得改进后的后向递推的平滑增益矩阵：

(27)

配合前向EKF滤波过程产生协方差矩阵，将式(25)-式(27)带入式(15)-式(17)即为本文改进的ERTSS-SLAM算法，其流程如图3所示。

图3 改进ERTSS-SLAM算法流程图Fig.3 Improved ERTSS-SLAM algorithm flowchart

3 实验及分析

3.1 实验平台

Turtlebot移动机器人平台是一款基于ROS操作系统的移动机器人[15]，其底盘采用韩国Kobuki平台，该底盘所自带的传感器类型及参数如表1所示。

表1 Turtlebot位姿传感器参数Table 1 The Parameters of Turtlebot Position and orientation sensor

图4 Turtlebot机器人及其简化模型Fig.4 Turtlebot robot and its simplified model

三轴数字陀螺仪采用意法半导体推出的高精度陀螺仪L3G4200D，具有低功耗、高精度、使用灵活的特点，实际应用中仅用单轴进行航向参数测量和惯性导航，而里程计精度高、体积小，是位置反馈的重要设备。Turtlebot移动机器人模型简化后如图4。

定义输入向量u=[Vα]T，加入过程噪声向量v=[vεvβ]T和检测噪声向量ω=[ωrωθ]T，对系统进行离散化计算得移动机器人的运动方程及观测方程[16-17]如下：

(28)

(29)

3.2 结果比较

为对比分析EKF-SLAM、ERTSS-SLAM和改进ERTSS-SLAM算法，选取分段数N=10，在MATLAB R2012a中建立11个路标(十字坐标点)的20 m×20 m地图(如图5)，并设置不规则障碍物(点线)和任意路径(圆线)。设置仿真时间500 s,采样周期T=10 ms，Wk为[-1.0,1.0]的白噪声，Vk为[-0.02，0.02]的白噪声信号，传感器感应距离10 m，对3种SLAM算法进行仿真对比。

图5 SLAM仿真地图Fig.5 SLAM simulation map

3种算法在SLAM定位过程中的定位误差结果如图6，由图6可知本文改进算法能有效提升移动机器人定位精度和稳定性。

图6 不同SLAM算法定位误差Fig.6 Different SLAM algorithms location error

3种SLAM算法在MATLAB R2012a中耗时及误差对比如表2所示。

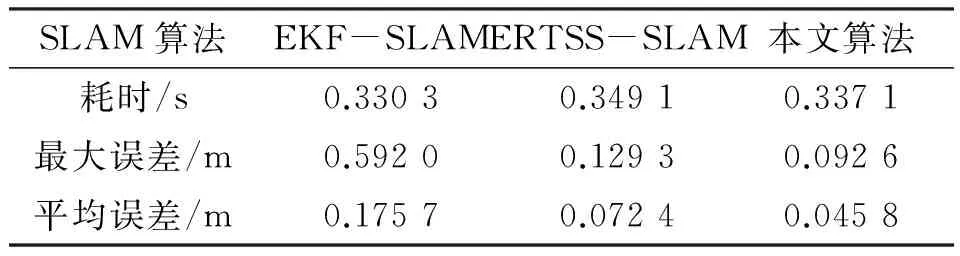
表2 不同SLAM算法性能比较Table 2 Performances of different smoothing algorithms

由表2分析知3种SLAM算法均能有效的抑制噪声信号，单独的EKF-SLAM算法稳定性较差；标准的ERTSS-SLAM算法在EKF基础上添加了ERTS平滑算法，多耗费0.118 s，但能提高精度58.8%；改进后的ERTSS-SLAM算法定位精度相较于其他两者分别提高了73.9%，36.7%，在耗时相近的情况下大幅提升了系统的精度和稳定性。

为了验证该算法在实际应用中的可行性及稳定性，本文在Turtlebot移动机器人进行了实际测试分析，其验证结果如表3。

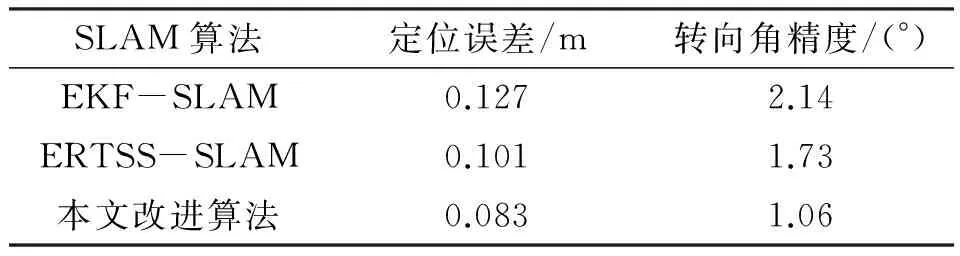
表3 Turtlebot机器人平台算法验证结果Table 3 Turtlebot robot platform algorithm validation results

3.3 抗干扰分析

现代控制对系统的鲁棒性要求越来越高，为验证本文改进算法在系统随机噪声干扰下的稳定性，分别增强测量噪声和系统噪声对3种算法进行定位误差比较，结果如图7。

定位误差

定位误差

图7 不同Wk和Vk扰动下的跟踪结果Fig.7 The location results with different Wk and Vk value

由图7分析可知该算法可以较好地稳定系统的输出，提高系统的定位精度，为SLAM中的地图构建提供可靠支撑。

4 结语

本文利用ERTS平滑算法的离线估计功能和奇异值分解法避免逆运算的优点，对标准EKF-SLAM进行了改进，提出了一种改进的EKF-SLAM算法。文中利用Turtlebot移动机器人平台的里程计和陀螺仪采集到的位姿信息进行前向扩展卡尔曼滤波器初步滤波后，通过奇异值分解法避免了EKF的求逆运算，并使用后向ERTS平滑算法离线估计，最终获得位置和姿态最优估计。仿真结果和实验证明该算法比标准的EKF-SLAM算法和ERTSS-SLAM算法具有更好的精确性和抗干扰能力。

[1] HUGH-DURRANT W, TIM Bailey. Simultaneous Localisation and Mapping (SLAM):Part I The Essential Algorithms[C]. 2010 International Conference on Intelligent Robots and Systems (IROS), 2010: 1-9.

[2] 杨乐,谢俐. 移动机器人SLAM问题新解[J]. 制造业自动化, 2013, 35(11): 43-46.

[3] BRADLEY H. Introduction to SLAM(Simultaneous Localization And Mapping)[R]. Las Vegas: Computer Science education, 2010.

[4] GURKAN T,Gulez Kayhan,Mumcu T.Veli. Evaluations of Different Simultaneous Localization and Mapping (SLAM) Algorithms[C].2012 IEEE ransactions on Robotics and Automation,2012: 2693-2698.

[5] LUIGI D, ANDREA G, PIETRO M. A SLAM algorithm for indoor mobile robot localization using an Extended Kalman Filter and a segment based environment mapping[C] Proceedings of the 2012 IEEE International Conference, 2013: 17-23.

[6] 张毅,赵黎明,罗元. 基于MIEKF的移动机器人同时定位与地图构建研究[J]. 计算机应用研究, 2011, 28(3): 902-904.

[7] WANG Dao-bin, LIANG Hua-wei,MEI Tao. Lidar Scan Matching EKF-SLAM Using the Differential Model of Vehicle Motion[C] 2013 IEEE Intelligent Vehicles Symposium (IV), 2013: 908-912.

[8] 杜航原,郝燕玲,赵玉新. 基于模糊自适应卡尔曼滤波的SLAM算法[J]. 华中科技大学学报:自然科学版, 2012, 40(1): 58-62.

[9] 石杏喜,赵春霞,郭剑辉. 基于PF/CUKF/EKF的移动机器人SLAM框架算法[J]. 电子学报, 2009, 37(8): 1865-1868.

[10] 王宏健,王晶,边信黔,等. 基于组合EKF的自主水下航行器SLAM[J]. 机器人, 2012, 34(1): 56-64.

[11] 武二永,项志宇,沈敏一,等. 大规模环境下基于激光雷达的机器人SLAM算法[J]. 浙江大学学报:工学版, 2007, 41(12): 1982-1986.

[12] 宫晓琳,张蓉,房建成. 固定区间平滑算法及其在组合导航系统中的应用[J]. 中国惯性技术学报, 2012, 20(6): 687-693.

[13] Razali Saifudin-Bin. Smoothing Techniques and a Spherical Simplex Unscented Transformation in Solving a SLAM Problem[D]. Okayama : Okayama University, 2012:44-50.

[14] 宫晓琳,房建成. 基于SVD的R_T_S最优平滑在机载SAR运动补偿POS系统中的应用[J]. 航空学报, 2009, 30(2): 311-318.

[15] SERGIO M, PAOLA L, LAURA S, et al. Localization and Mapping Approximation for Autonomous Ground Platforms, Implementing SLAM Algorithms[C].2014 IEEE,2014: 139-145.

[16] ZHU J H, ZHENG N N, YUAN Z J, et al.A SLAM Algorithm Based On The Central Difference Kalman Filter [C].2009 Intelligent Vehicles Symposium IEEE，2009：123-128.

[17] ZHANG H T, RONG J, ZHONG X C. The Performance Comparison And Algorithm Analysis Of First/Second Order EKF And Smoother For GPS/DR Navigation [C]. 11th IEEE Inter. Conf. on Comm. Technology. 2008: 432-437.

Improved EKF-SLAM Method and Its Implementation on the Turtlebot

XUE Yong-sheng, WANG Heng, ZHANG Hua, HUO Jian-wen

(KeyLaboratoriesforSpecialEnvironmentRobotTechnologyofSichuanProvince,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan,China)

Targeting to tackle those problems like too massive calculation, weak timeliness, low accuracy and robustness, etc., during the process of the mobile robot’s simultaneous localization and mapping (SLAM) by using the way of the standard extended Kalman filter (EKF), combining the smoothing algorithm and singular value decomposition algorithm, a new SLAM algorithm (ERTSS-SLAM) is proposed in this paper. By the forward EKF method, the improved ERTSS-SLAM algorithm conducts the optical pose estimation of the mobile robot’s odometer and gyroscopes pose information and then avoid dispersion with the standard ERTS smoother, and at the same time, the inverse calculation is prevented by using the singular value decomposition algorithm, so as to enhance the system’s timeliness, robustness and accuracy accordingly. Experimental results on the Turtlebot show that the new ERTSS-SLAM algorithm is very efficient and stable during the SLAM application.

Simultaneous localization and mapping; Smoothing algorithm; Singular Value Decomposition; Turtlebot

2014-10-10

四川省科技厅科技支撑计划项目(2014RZ0049)；2014四川省科技支撑计划项目(2014GZ0021)。

薛永胜(1989—)，男，硕士研究生，研究方向为工业智能控制、智能检测技术。E-mail:xys1989225@163.com

TP273+.2

A

1671-8755(2015)01-0054-06