DNA双链断裂损伤修复的随机模型研究*
2015-06-06孙廷哲
孙廷哲,崔 隽
(1.安庆师范学院生命科学学院,安徽安庆246011;2.基因工程教育部重点实验室//中山大学生命科学学院,广东广州510275)
电离辐射以及某些化学诱变剂所诱导的DNA双链断裂损伤 (DNA double strand break,DSB)是一种非常严重的 DNA损伤[1]。如果细胞不能对DNA双链断裂进行恰当的修复,通常会导致基因组突变或者细胞死亡。细胞中持续的DNA双链断裂损伤也会大大增加癌变的风险。所以,DNA双链断裂修复对维持基因组的稳定性起到了至关重要的作用[2]。
除了外源性因素所诱导的DNA双链断裂之外,内源性的因素也会导致DNA双链断裂损伤。约1%的单链DNA断裂损伤 (single-strand DNA lesion,SSL)会转变为双链DNA损伤。同时,在同源染色体的重组过程中,DNA双链断裂损伤也有一定的几率生成。有报道称,在具有Bloom综合征遗传背景细胞中,一个细胞周期约有50个内源性DNA双链断裂产生,而正常细胞中内源性DSB水平相应降低[3]。这相当于1.5 ~2 Gy的电离辐射所诱导的DNA双链断裂。在肿瘤细胞中,内源性即本底水平的DNA双链断裂则更为显著[4]。
在真核细胞中,DNA双链断裂的修复主要通过两种方式:一种是同源重组 (homologous recombination,HR),另一种是非同源末端连接 (nonhomologous end joining,NHEJ)[3]。譬如 MRN 复合物(由 Mre11,Rad50和 NBS1组成)、ATM(Ataxia Telangiectasia Mutated)MDC1和BRCA1等相关蛋白都参与到双链断裂的修复过程中。对DSB损伤修复的动力学研究一直是重要的课题。同时,通过系统生物学方法对DSB修复进行的模型研究也不断涌现。早期的LPL(lethal and potentially lethal)模型以及RMR(repair-misrepair)模型是具有代表性的两类模型[5-6]。这些模型通过引入可能的一级和二级动力学修复过程,较好的解释了辐射诱导的细胞死亡现象。但是,对于双链断裂损伤所引发的细胞死亡动力学,这两类模型不能很好的进行拟合。基于进一步的实验研究,Stewart提出了TLK模型 (Two-Lesion Kinetic Model)[7]。在 TLK 模型中,根据DNA双链断裂产生的复杂程度,修复经历了快修复和慢修复两种过程。基于TLK模型的基本假设,Ma等[8]利用Monte Carlo方法构建了一个抽象的数学模型,很好的模拟了DNA双链断裂损伤的动力学行为并因此成功的解释了p53的数字脉冲现象。Ma等提出的模型被很多后续的研究者所借鉴,为进一步的解释细胞命运决定机制起到了极大的推动作用。另外,其他的一些模型则通过引入具体的分子机制对DNA双链断裂损伤的修复进行了动态的研究[9-12]。
但是,以上的这些模型并没有充分考虑到细胞周期和DNA双链断裂损伤产生及修复的联系:即只考虑了电离辐射诱导产生的外源性DNA双链断裂的动态修复,而并没有考虑内源性DNA双链断裂的动态变化。在辐射刺激下,细胞会发生细胞周期阻滞现象,并修复辐射诱导的DNA损伤。当DNA损伤降低到特定阈值以下,细胞周期将被重启。细胞周期重启后,细胞周期伴随的内源性DNA双链断裂将不断产生,并得到动态修复。所以,我们提出了一个改良的Monte Carlo模型,并综合考虑了外源性和内源性DNA双链断裂损伤的动态修复过程,从而更真实的模拟了细胞在应激状态下的DNA双链断裂损伤修复的动力学行为。
1 材料与方法
1.1 DNA双链断裂损伤概述
DNA双链损伤修复模型分为两个模块:分别为辐射诱导 (外源性)DNA损伤修复和内源性DNA损伤修复模块。两个模块都基于Stewart模型的基本假设,即根据损伤的复杂程度,DSB修复分为快修复和慢修复两种动力学形态[7]。DNA修复过程通过Monte Carlo过程来模拟。在修复过程中,DSB可能处于3种不同的状态:①完整的DSB;②DSB和修复蛋白的复合物;③已修复DSB。根据Ma等的假设,本模型暂不考虑错误修复情形[8]。在时间步为k时,处于状态①、②和③的DSB分别用D(k),C(k)和F(k)来表示。我们用下标‘1’和‘2’来区分DSB的快速修复和慢速修复过程 (图1A)。易得如下关系:D(k)=D1(k)+D2(k),C(k)=C1(k)+C2(k)和 F(k)=F1(k)+F2(k).总的修复蛋白(Repair protein,RP)被设定为20。随机模拟的时间步长Δt设定为0.2 min。

图1 DSB修复模型Fig.1 DSB repair modelA:快修复和慢修复动力学图示;B:内源性DSB生成和时间步长关系
1.2 外源性和内源性DSB数目初始化
1.2.1 辐射诱导的DNA双链断裂修复 根据文献报道,1 Gy的辐射剂量约产生30个DSB[3]。为了充分考虑DSB生成的随机化,根据Ma等的假设,我们设定DSB的生成服从Poisson分布,其参数λ=30·IR,这里IR为辐射剂量[8]。根据Ma等的假设,70%的总DSB被快修复,而剩余的30%的DSB经历慢修复过程。
1.2.2 内源性DNA双链断裂修复 假设内源性的DSB主要在细胞周期过程中产生。进一步限定,所有的DSB均在细胞周期中的S期和G2/M期产生,并服从均匀分布。为了简化模型,对细胞周期的时长进行了限定,即长度为20 h,其中G1,S和G2/M期的比例设为3∶4∶3。如文献报道,乳腺癌肿瘤细胞MCF7的细胞周期约为20 h,其中G1,S和G2/M期时长分别为6、8和6 h,且周期不受外源辐射刺激影响[13]。本模型关于细胞周期的时长以及内源性DSB发生时间的设定亦可设为它值 (包括设置为随机变量),且不会对模型动力学产生定性的影响。在一个细胞周期中,我们设定将有50个DSB发生[3]。由于同源染色体重组等事件可诱发DSB,所以 DSB产生主要处于 S期[3]。因此,假设其中40个产生于S期,剩余10个产生于G2/M期。在内源性DNA损伤修复模块中,我们设定每一个生成的内源性DSB将有70%的概率被快修复,有30%的概率被慢修复。
1.3 DSB修复的一般过程
为了偶联外源性和内源性DSB修复的过程,我们设定发生细胞周期阻滞 (cell cycle arrest)的阈值为50个DSB。有文献报道,正常细胞中当DSB水平小于20时,细胞周期阻滞将停止[14]。但肿瘤细胞可以耐受更高水平的DNA损伤[4],所以我们将肿瘤细胞的阈值相应提高。当总DSB数目≤50时,细胞周期将被重启。DSB的修复遵循如下过程:
1)设置初始值。D1(0)=floor(0.7·DSBT),D2(0)=DSBT-D1(0),这里DSBT为服从参数为λ的Poission分布随机数,floor为向下取整。新生的外源性和内源性DSB都处于状态1。设k=0。
2)增加时间步。设t=t+Δt,k=k+1。如果在 [t,t+Δt]之间有1个内源性DSB生成 (图1B,注:细胞周期重启后),则令D1(k)=D1(k)+1(概率为0.7,快速修复)或D2(k)=D2(k)+1(概率为0.3,慢速修复)。
3)对每一个进行快速修复的各状态DSB进行更新。计算状态转变的概率:
从状态①->状态②,
PD1->C1=RP [kfb1+kcross(D1(k-1)+D2(k-1))]Δt
从状态②->状态①,
PC1->D1= krb1Δt。
从状态②->状态③,
PC1->F1= kfix1Δt。
对于每一个DSB,首先生成一个 [0,1]均匀分布的随机数x。如果0≤ x< PD1->C1,处于状态①的DSB将转变为状态②;如果PD1->C1≤ x≤1,那么DSB将维持在状态①。若DSB处于状态②,那么如果0≤ x<PC1->D1,状态②将转变为状态①。如果 PC1->D1≤ x < PC1->D1+ PC1->F1,那么状态②将转变为状态③。若PC1->D1+PC1->F1≤x≤1,那么状态②将维持不变。如果损伤处于状态③,那么它将维持不变 (即状态③是吸收态)。修复蛋白RP遵循如下规律:如果发生状态①到状态②转变,设RP=RP-1;反之则设RP=RP+1。其它情况下,RP维持不变。对处于状态①、②和③的DSB进行计数,并分别赋予D1(k),C1(k)和 F1(k)。
4)类似于快修复过程,对慢修复DSB进行更新。算法如下:
从状态①->状态②,PD2->C2=RP [kfb2+kcross(D1(k-1)+D2(k-1))]Δt。
从状态②->状态①,
PC2->D2= krb2Δt。
从状态②->状态③,
PC2->F2= kfix2Δt。
对于每一个慢修复DSB,首先生成一个 [0,1]均匀分布的随机数x。如果0≤ x < PD2->C2,状态1的DSB将转变为状态2;如若PD2->C2≤ x≤1,那么将维持在状态①。若DSB处于状态②,如果0≤ x<PC2->D2,状态②将转变为状态①。如果 PC2->D2≤ x < PC2->D2+ PC2->F2,那么状态②将转变为状态③。若 PC2->D2+ PC2->F2≤ x≤1,那么状态②将维持不变。如果损伤处于状态③,那么它将维持不变 (即状态③是吸收态)。修复蛋白RP遵循如下规律:如果发生状态①到状态②转变,设RP=RP-1;反之则设RP=RP+1。其它情况下,RP维持不变。对处于状态①、②和③的DSB进行计数,并分别赋予D2(k),C2(k)和F2(k)。
5)令 D(k)=D1(k)+D2(k),C(k)=C1(k)+C2(k),和F(k)=F1(k)+F2(k)。
6)重复 (2)- (5),直到t=tfinal。
DNA修复模块各参数详见表1。

表1 模型参数和描述1)Table 1 Model parameter and description
1.4 DSB修复模型模拟工具
随机模拟通过MATLAB(MathWork,版本号7.12.0.635,R2011a)实现。
2 结果
2.1 DSB修复的动态变化
通过运行MATLAB脚本程序,获得了200组Monte Carlo模拟结果。图2中对应的初始外源性辐射刺激为5 Gy。具体为:产生200个随机数,这些随机数服从λ=150(5×30)的Poisson分布。接着将200个随机数作为初始刺激水平。随机数的产生运用到了MATLAB的库函数poissrnd。产生的200组初始DSB分布可参见图2A。图2B示部分随机DSB修复模型的模拟结果。发现DSB的修复在时间序列上呈现出很大的变异性,表现在每个细胞初始的DSB水平不同,这种变异是由所产生的200组符合Poisson分布的随机数引起的。同时,细胞中DSB的修复速率也存在较大变异。当细胞重新进入细胞周期后,DSB的修复往往呈现一种非单调的动态变化 (图2B)。一些自发产生的内源性DNA损伤使得总体DSB数目经历不同水平的瞬间上升。当自发DNA损伤产生较集中而修复能力相对较弱时,总体DSB水平会有更为显著的升高(图2B,左图)。我们也注意到:在外源辐射施加24 h后,细胞中仍然存在较高水平的DNA双链损伤 (图2B)。即使将模拟时间延长到48 h,这种动态行为仍然存在 (图2C)。我们分别统计了200组随机模拟试验中最低的DSB水平 (注:时长为48 h)。从柱状图中我们可以发现,所有的200组模拟结果都表明细胞中存在着未被修复的DNA损伤,同时在某些细胞中,DNA损伤可能一直维持在较高的水平 (图2C)。这些结果表明,细胞中DSB修复存在着较为显著的变异,同时细胞也具有较高水平的本底DNA损伤。
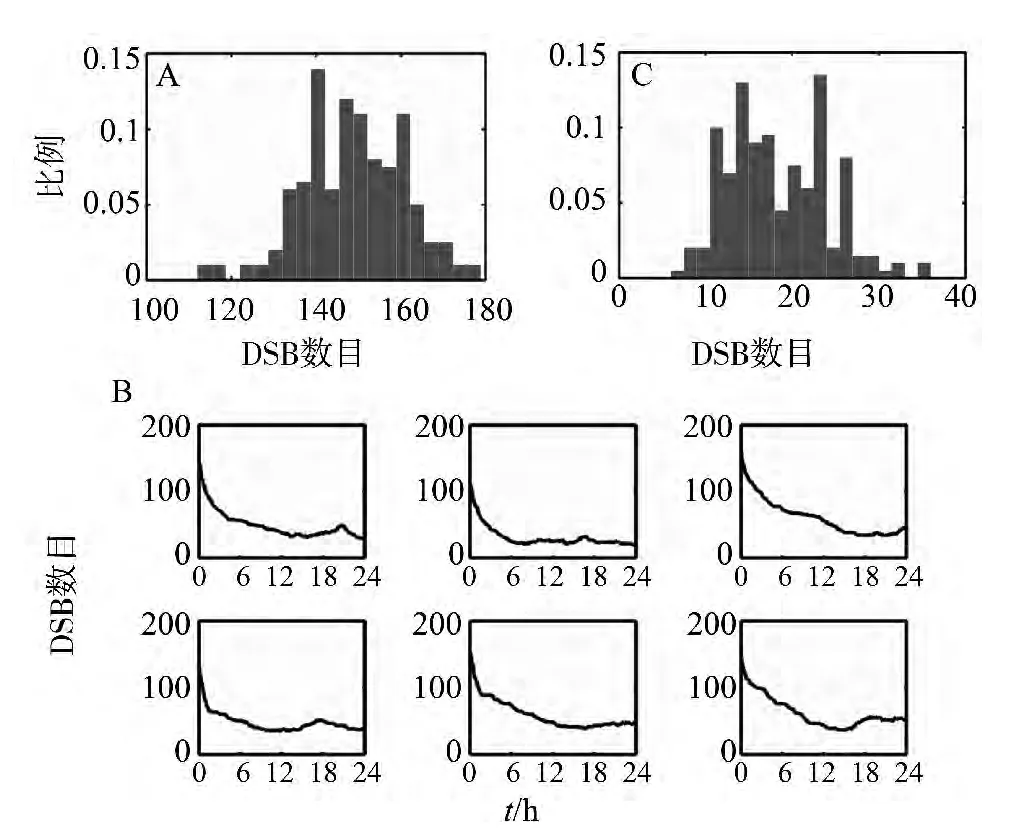
图2 DSB随机修复动力学行为Fig.2 Dynamics of stochastic repairA:初始DSB分布 (服从参数为150的Poisson分布);B:DSB随机修复的动态变化;C:在48 h内,每次模拟中最小DSB值分布图 (共200组)
2.2 DSB修复过程中的变异性
从图2可知DSB修复的动态过程存在着较大的变异性。为了进一步描述这种变异行为,对200组时间序列进行描述性统计。结果显示,DSB的修复存在着较为显著的变异性 (图3A)。在DSB修复的初期,这种变异性较小,表现为较窄的置信区间。从平均水平上而言,DSB修复过程的半衰期(即令 DSB水平下降到初值一半的时间)约为3.24 h。而从约2 h到10 h这段时间内,DSB修复的变异相对较大 (图3A)。这种相对较显著的变异可能是由早期外源性DNA的随机修复引起的。与内源性DSB不同的是,外源DSB的发生服从Poisson分布,从而在随机修复的基础上引入了额外的不确定性。随着时间的推移,随机修复合并初值随机分布的变异将愈发显著,进而可能导致DSB的修复在半衰期附近存在较大变异。当较多的外源性DSB得到了修复后,总DSB接近于重新触发细胞周期的水平。由于未被修复的DSB水平较之初始状态显著降低,所以随机修复的变异也随之下降。进一步统计了200组模拟的半衰期。结果显示,DSB的半衰期亦存在着较为明显的变异 (图3B)。同时,半衰期的分布与时间序列中变异较为显著的区域也具有一定的吻合。以上结果暗示,DSB的损伤修复具有较为显著的变异性。

图3 DSB修复过程中的变异Fig.3 Variations in DSB repairA:200组Monte Carlo模拟的平均值 (红色曲线)和95%置信区间 (红色阴影区);B:DSB修复半衰期分布
3 讨论
本文提出了一个更为精细化的DNA双链断裂损伤修复模型。在这个模型中,考虑了外源性和内源性DSB在修复过程中的偶联,并对此模型进行了Monte Carlo模拟。模拟结果显示,DSB的修复具有显著的变异性 (图2、图3)。同时,由于本底水平即内源性DNA损伤的随机发生,DSB的动态变化并非呈现一种单调降低的行为 (图2B)。这种非单调的行为是以往的模型所忽视的。最近Loewer等[15]的实验显示肿瘤细胞中的DNA双链损伤可能呈现非单调的动态行为,从而为本文模拟结果提供了依据。所以,本文模型可以较好的模拟细胞完整生命周期中的DSB损伤修复行为。
值得注意的是Ma等之前的模型并没有考虑具体的DSB修复信号转导网络,转而根据TLK的基本假设提出了一个较为抽象的模型。其优势在于DSB修复的信号转导网络仍存在较大的未知,且已知参与修复的蛋白复合物相互作用较为复杂[16-17]。若采用常规的常微分方程建模方法,将极大的增加模型的复杂程度。运用抽象的Monte Carlo模拟方法既能较好的模拟DSB修复的随机动力学行为,同时又能巧妙的回避具体信号转导网络的未知因素。所以,本文基于Ma等的模型,提出了DSB修复的更为完整的模型,即同时考虑内源性和外源性DSB损伤的修复过程及其偶联效应,更好的描述了细胞在应激状态下的DSB修复过程。需要注意的是,本模型参数主要基于肿瘤细胞相关研究进行的估计,所以此模型旨在描述非正常细胞的DSB修复行为[18]。对于正常的细胞而言,本底水平的DSB数量较之肿瘤细胞显著的降低,同时触发细胞周期阻滞的DSB阈值也较低。同时,肿瘤细胞中的基因突变很可能导致正确修复速率的显著降低[19-20]。综合以上的因素,正常细胞中的DSB修复可能具有更高的效率,从而使得正常细胞中的DSB修复动力学性质可能会与肿瘤细胞中的相关性质具有一定的差异。通过改变模型参数 (如增大kfix1或减少内源性DSB总量),即可对正常细胞的DSB修复进行定性的模拟。所以,本模型具有一定的普适性。
提出较为完整的DSB修复模型对于其它信号转导网络的相关动力学行为研究也具有很大的必要性。譬如ATM可以作为感受器感知DSB的变化,并得到活化。活化的ATM可以作为激酶磷酸化p53蛋白并借此与复杂的p53信号转导网络建立直接的联系。P53在未受刺激和应激状态下 (如电离辐射和紫外线)都表现出复杂的动力学行为[13,15,21-23]。以往描述 p53 动力学模型中的 DNA损伤修复模块都没有很好的考虑外源性和内源性DNA损伤的协同作用,所以不能很好的同时解释p53 在受迫和未受迫状态下的动力学行为[22,24-25]。所以,本模型可能有助于其它信号转导网络的动力学行为研究。譬如内源性的DNA损伤会在非受迫状态下触发p53的自发脉冲,那么就为研究p53的本底动力学和p53单细胞动力学中存在的线性现象提供了可能[13,15]。此外,DSB 修复模型与细胞周期信号转导网络的偶联也可能有助于模拟更为真实的细胞周期中的动力学现象[26]。DNA损伤修复与特定信号转导网络的相互作用也可能产生反馈或前馈作用,从而产生更为复杂的动力学行为。
随着对DNA双链断裂损伤修复过程认识的不断深入,建立更为精细化的基于具体分子机制的DNA损伤修复模型并结合恰当的随机模拟方法将有助于实现对损伤修复过程更为精确的定量研究。
[1]BEKKER-JENSEN S,MAILAND N.Assembly and function of DNA double-strand break repair foci in mammalian cells[J].DNA Repair(Amst),2010,9(12):1219-1228.
[2]KARRAN P.DNA double strand break repair in mammalian cells[J].Current Opinion in Genetics& Development,2000,10(2):144-150.
[3]VILENCHIK M M,KNUDSON A G.Endogenous DNA double-strand breaks:Production,fidelity of repair,and induction of cancer[J].Proceedings of the National A-cademy of Sciences of the United States of America,2003,100(22):12871-12876.
[4]OLIVIER M,BAUTISTA S,VALLES H,et al.Relaxed cell-cycle arrests and propagation of unrepaired chromosomal damage in cancer cell lines with wild-type p53[J].Molecular Carcinogenesis,1998,23(1):1-12.
[5]CURTIS S B.Lethal and potentially lethal lesions induced by radiation-a unified repair model[J].Radiation Research,1986,106(2):252-270.
[6]TOBIAS C A.The repair-misrepair model in radiobiology:comparison to other models[J].Radiation Research Suppl,1985,8 S77-95.
[7]STEWART R D.Two-lesion kinetic model of doublestrand break rejoining and cell killing[J].Radiation Research,2001,156(4):365-378.
[8]MA L,WAGNER J,RICE J J,et al.A plausible model for the digital response of p53 to DNA damage[J].Proceedings of the National Academy of Sciences of the United States of America,2005,102(40):14266-14271.
[9]MOURI K,NACHER J C,AKUTSU T.A mathematical model for the detection mechanism of DNA double-strand breaks depending on autophosphorylation of ATM [J].PLoS One,2009,4(4):e5131.
[10]TALEEI R,NIKJOO H.The non-homologous end-joining(NHEJ)pathway for the repair of DNA doublestrand breaks:I.A mathematical model[J].Radiation Research,2013,179(5):530-539.
[11]TALEEI R,GIRARD P M,SANKARANARAYANAN K,et al.The non-homologous end-joining(NHEJ)mathematical model for the repair of double-strand breaks:II.Application to damage induced by ultrasoft X rays and low-energy electrons[J].Radiation Research,2013,179(5):540-548.
[12]LAKOMIEC K,KUMALA S,HANCOCK R,et al.Modeling the repair of DNA strand breaks caused by gamma-radiation in a minichromosome[J].Physical Biology,2014,11(4):045003.
[13]LOEWER A,BATCHELOR E,GAGLIA G,et al.Basal Dynamics of p53 Reveal Transcriptionally Attenuated Pulses in Cycling Cells[J].Cell,2010,142(1):89-100.
[14]DECKBAR D,BIRRAUX J,KREMPLER A,et al.Chromosome breakage after G2 checkpoint release [J].Journal of Cell Biology,2007,176(6):749-755.
[15]LOEWER A,KARANAM K,MOCK C,et al.The p53 response in single cells is linearly correlated to the number of DNA breaks without a distinct threshold [J].BMC Biology,2013,11:114.
[16]SHILOH Y,ZIV Y.The ATM protein kinase:regulating the cellular response to genotoxic stress,and more[J].Nature Reviews Molecular Cell Biology,2013,14(4):197-210.
[17]LIU C,SRIHARI S,CAO K A,et al.A fine-scale dissection of the DNA double-strand break repair machinery and its implications for breast cancer therapy[J].Nucleic Acids Research,2014,42(10):6106-6127.
[18]张久远,冯兆永,刘成霞,等.关于肿瘤细胞破坏并入侵正常组织或细胞质基质的数学模型的分析[J].中山大学学报:自然科学版,2015,52(3):48-54.
[19]TUTT A,BERTWISTLE D,VALENTINE J,et al.Mutation in Brca2 stimulates error-prone homology-directed repair of DNA double-strand breaks occurring between repeated sequences [J].EMBO Journal,2001,20(17):4704-4716.
[20]KHANNA K K,JACKSON S P.DNA double-strand breaks:signaling,repair and the cancer connection[J].Nature Genetics,2001,27(3):247-254.
[21]LAHAV G,ROSENFELD N,SIGAL A,et al.Dynamics of the p53-Mdm2 feedback loop in individual cells[J].Nature Genetics,2004,36(2):147-150.
[22]GEVA-ZATORSKY N,ROSENFELD N,ITZKOVITZ S,et al.Oscillations and variability in the p53 system[J].Molecular Systems Biology,2006,2(1):20060033.
[23]BATCHELOR E,LOEWER A,MOCK C,et al.Stimulus-dependent dynamics of p53 in single cells[J].Molecular Systems Biology,2011,7(1):488.
[24]OUATTARA D A,ABOU-JAOUDE W,KAUFMAN M.From structure to dynamics:frequency tuning in the p53-Mdm2 network.II Differential and stochastic approaches[J].Journal of Theoretical Biology,2010,264(4):1177-1189.
[25]KIM J K,JACKSON T L.Mechanisms that enhance sustainability of p53 pulses[J].PLoS One,2013,8(6):e65242.
[26]TOETTCHER J E,LOEWER A,OSTHEIMER G J,et al.Distinct mechanisms act in concert to mediate cell cycle arrest[J].Proceedings of the National Academy of Sciences of the United States of America,2009,106(3):785-790.
