von Neumann代数上的Jordan双导子

王莉莉，张建华

（陕西师范大学数学与信息科学学院，陕西西安710119）

von Neumann代数上的Jordan双导子

王莉莉，张建华＊

（陕西师范大学数学与信息科学学院，陕西西安710119）

证明了无非零中心理想von Neumann代数上的Jordan双导子是内双导子。作为应用，给出了无非零中心理想von Neumann代数中所有自伴算子构成的实Jordan代数上Jordan双导子的具体结构。

von Neumann代数；双导子；Jordan双导子

设A是一个代数，其中心记为Z（A）。如果一个映射f：A→A满足∀x、y∈A有f（x+y）－f（x）－f（y）∈Z（A）成立，则称f是A上的模中心可加映射。如果一个映射f：A→A满足对任意的x∈A有［f（x），x］＝0，则称f为A上的交换映射，其中［x，y］＝xy－yx为x与y的Lie积。设δ：A→A是一个线性映射。如果∀x、y∈A，有δ（xy）＝δ（x）y+ xδ（y），则称δ是A上的导子；如果存在a∈A使得∀x∈A，有δ（x）＝xa－ax，则称δ是A上的内导子。如果∀a∈A，有δ（a2）＝δ（a）a+aδ（a），则称δ是A上的Jordan导子。显然，导子一定是Jordan导子，反之不成立。

设φ：A×A→A是一个双线性映射。如果对每一个y∈A，映射x→φ（x，y）和x→φ（y，x）都是A上的导子，则称φ是A上的双导子；如果存在a∈ Z（A）使得∀x、y∈A，有φ（x，y）＝a［x，y］，则称φ是A上的内双导子。如果对每一个y∈A，映射x→φ（x，y）和x→φ（y，x）都是A的Jordan导子，则称φ是A上的Jordan双导子。显然，双导子一定是Jordan双导子，反之不成立。

导子、Jordan导子与双导子是代数或环上的重要映射，它们对代数或环的结构及相关问题的研究具有重要的作用。一直以来，关于代数或环上导子、Jordan导子与双导子的研究备受关注，并涌现出许多深刻结论［1－4］。文献［5］证明了半素环上的Jordan导子一定是导子。文献［6］得到了素环上双导子的具体结构。文献［7］给出了套代数上双导子都是内双导子的充要条件。文献［8］证明了可交换环上的上三角矩阵代数中的双导子是极值双导子与内双导子之和。文献［9］给出了三角代数上的双导子是极双导子与内双导子之和的充分条件。文献［10］给出了广义矩阵代数上的双导子是极双导子与内双导子之和的充分条件。von Neumann代数是一类不满足文献［10］中条件的算子代数，本文将考虑von Neumann代数上的Jordan双导子以及von Neumann代数中自伴算子全体构成的实Jordan代数上的Jordan双导子。

1 几个引理

设R是一个半素环，Q是R的Martindale商环，则R可以同构嵌入Q，从而可看成Q的一个子环。记C＝｛q｜q∈Q且对任意的x∈R有qx＝xq｝，并称其为R的扩展中心。

引理1 设R是一个半素环，f：R→R是一个模中心可加交换映射，则存在λ∈C及映射ζ：R→C使得f（x）＝λx+ζ（x）对任意的x∈R成立，其中C是R的扩展中心。

证明 由于f：R→R是一个模中心可加交换映射，在［f（x），x］＝0中用x+y替换x，则对任意x、y∈R，有［x，f（y）］＝［f（x），y］。设φ（x，y）＝［f（x），y］，则φ：R×R→R是一个可加双导子。由文献［11］中定理4.1，从而存在η∈C及幂等元e∈C使得（1－e）R可交换，且对任意的x、y∈R，有eφ（x，y）＝eη［x，y］。由φ的定义，则对任意的x、y∈R，有［ef（x）－eηx，y］＝0，从而对任意的x∈R，有ef（x）－eηx∈C。记λ＝eη，并定义映射ζ：R→C为ζ（x）＝（ef（x）－λx）+（1－e）f（x）。于是，f（x）＝λx+ζ（x）对任意的x∈R成立。证毕。

引理2 设R是一个含单位元的半素环，f：R→R是模中心可加映射。如果对任意的x、y∈R，有［x，f（yx）－f（y）x］＝0，则存在a∈R及映射ζ：R→C使得对任意的x∈R，有f（x）＝ax+ζ（x）成立，其中C是R的扩展中心。

证明 在［x，f（yx）－f（y）x］＝0中，取y＝1，则对任意的x∈R，有［x，f（x）－f（1）x］＝0。定义映射g：R→R为g（x）＝f（x）－f（1）x，则g是R上的模中心可加映射，且对任意的x∈R，有［x，g（x）］＝0。由引理1，从而存在λ∈C及映射ζ：R→C使得对任意的x∈R，有g（x）＝λx+ζ（x）。于是对任意的x∈R，有f（x）＝ax+ζ（x），其中a＝λ+f（1）。证毕。

引理3 设R是一个半素环，如果存在a∈R使得任意的x、y∈R，有［x，y］a＝0，则a∈Z（R）。

证明 对任意的x、z∈R，有

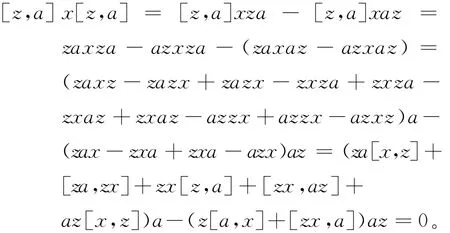
由R的半素性，则对任意的z∈R，有［z，a］＝0。从而，a∈Z（R）。证毕。

引理4 设R是一个无非零中心理想含单位元的半素环，f、g：R→R是映射，且满足下列条件之一：

（1）对任意的x、y∈R，有xf（y）+yg（x）＝0；

（2）对任意的x、y∈R，有f（x）y+g（y）x＝0，则对任意的x∈R，有f（x）＝g（x）＝0。

证明 假设条件（1）成立，在xf（y）+yg（x）＝0中，取x＝1，则对任意的y∈R，有f（y）＝－yg（1）；取y＝1，则对任意的x∈R，有g（x）＝－xf（1）；取x＝y＝1，则f（1）+g（1）＝0。从而对任意的x、y∈R，有

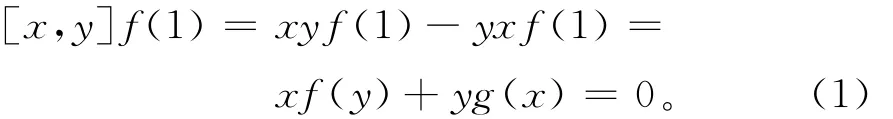
由引理3，则f（1）∈Z（R）。令I＝｛xf（1）：x∈R｝。显然，I是R的一个理想。由（1）式，对任意的z∈R，y∈I，有［z，y］＝0，从而I⊆Z（R）。这说明I是R的一个中心理想。由于R无非零中心理想，则f（1）∈I＝｛0｝。因此，对任意的x∈R，有f（x）＝g（x）＝0。类似可得，在条件（2）下，结论也成立。证毕。

下面的例子说明引理4中的条件“R无非零中心理想”不可少。

例1 设R1是一个含单位元的半素环，R2＝Z为整数环，则

R＝R1⊕R2＝｛（x，n）：x∈R1，n∈R2｝。

在运算（x，n）+（y，m）＝（x+y，n+m）和（x，n）（y，m）＝（xy，nm）下是一个含单位元的半素环，并且M＝｛（0，n）：n∈R2｝是R的一个非零中心理想。定义映射f、g：R→R如下：

f（（x，n））＝（0，n），g（（x，n））＝（0，－n）。则对任意的x＝（u，n）、y＝（v，m）∈R，有xf（y）+ yg（x）＝0。但f、g均为非零映射。

引理5［6］设R是一个环，f1、f2、f3、f4：R→R为映射。如果对任意的x、y∈R，有

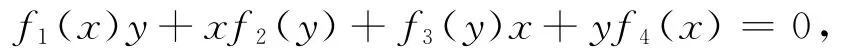
则对任意的x、y、z∈R，有

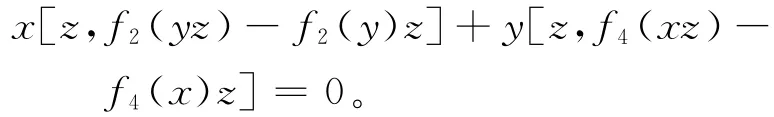
引理6 设R是一个无非零中心理想含单位元的半素环，f1、f2、f3、f4：R→R是模中心可加映射，且对任意的x、y∈R，有

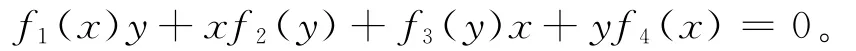
则存在a、b∈R及映射ζ、ξ：R→C使得

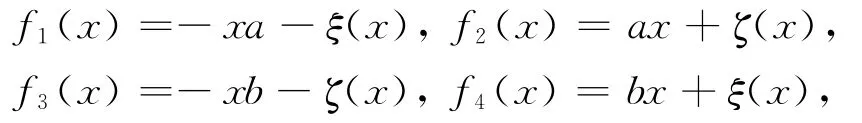
对任意的x∈R成立。

证明 由引理5，则对任意的x、y、z∈R，有

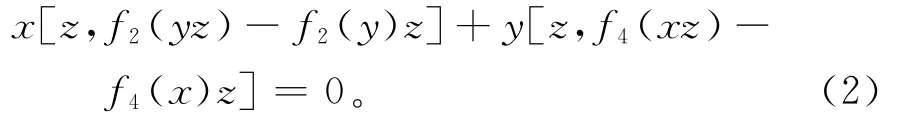
对任一z∈R，定义映射gz、hz：R→R为

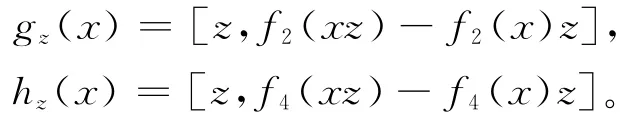
由（2）式，则对任意的x、y∈R，有xgz（y）+ yhz（x）＝0。从而由引理4及gz、hz的定义，对任意的x、z∈R，有

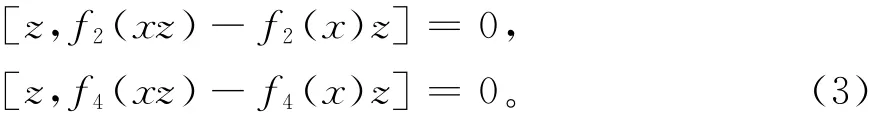
由（3）式和引理2，则存在a、b∈R及映射ζ、ξ：R→C使得对任意的x∈R，有

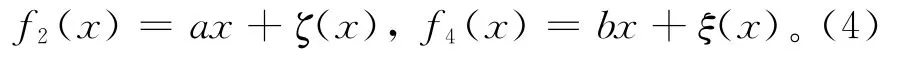
将（4）式代入f1（x）y+xf2（y）+f3（y）x+ yf4（x）＝0并整理得：对任意的x、y∈R，有

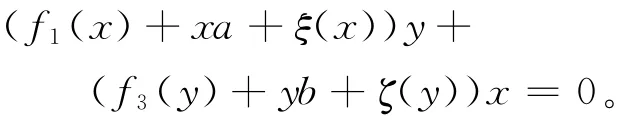
再由引理4，则对任意的x∈R，有

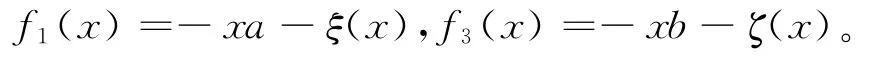
证毕。

2 主要定理及应用

von Neumann代数是一类半素的算子代数，并且其扩展中心与中心相同。本节将讨论von Neumann代数上的Jordan双导子，并得到以下主要定理。

定理1 设A是一个无非零中心理想的von Neumann代数，φ：A×A→A是Jordan双导子。则存在a∈Z（A）使得对任意的x、y∈A，有φ（x，y）＝a［x，y］。

证明 由于von Neumann代数A上的Jordan导子是导子并且A上的导子是内导子［4］，则对任一固定的y∈A，φ：（·，y）是A上的内导子，从而存在映射f：A→A使得对任意的x∈A，有

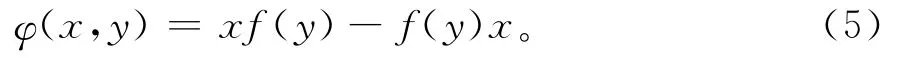
同样地，对任一固定的x∈A，由于φ（x，·）是A上的内导子，则存在映射g：A→A使得对任意的y∈A，有

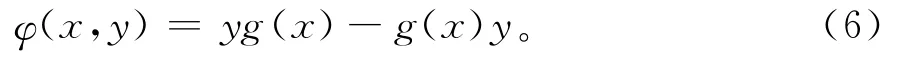
由（5）式，对任意的y、z∈A，有

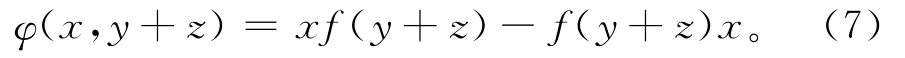
另一方面，

于是，f（y+z）－f（y）－f（z）∈Z（A）。即f是A上的模中心可加映射。类似可得g也是A上的模中心可加映射。由（5）式和（6）式知，对任意的x、y∈A，有

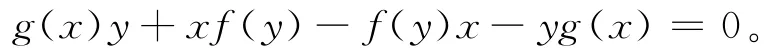
由引理6，则存在a、b∈A及映射ζ、ξ：A→Z（A）使得对任意的x∈A，有

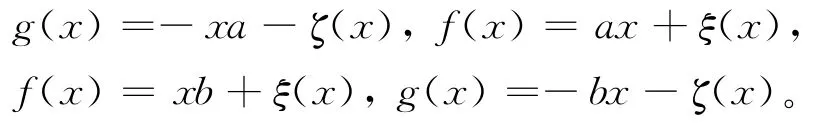
这说明对任意的x∈A，有ax＝xb。从而a＝b且a∈Z（A）。因此，由（5）式，对任意的x、y∈A，有

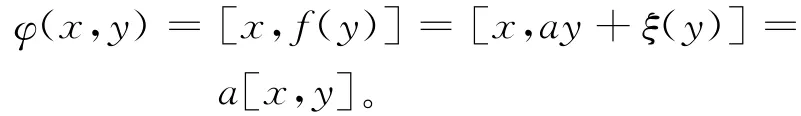
证毕。

设As表示Von Neumann代数A中的自伴算子全体，则As在Jordan积x◦y＝xy+yx下是一个实Jordan代数。作为定理1的一个应用，可得到实Jordan代数As上Jordan双导子的如下结论：

定理2 设A是一个无非零中心理想的von Neumann代数，φ：As×As→As是Jordan双导子。则存在自伴算子a∈Z（A）使得对任意的x、y∈As，有φ（x，y）＝i a［x，y］。

证明 设x∈A，以下用xr和xi分别表示x的实部和虚部。即

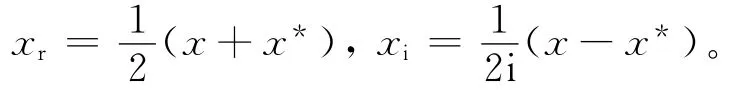
显然，xr、xi∈As且x＝xr+i xi。设φ：As×As→As是一个Jordan双导子。定义映射：~φ：A×A→A如下：

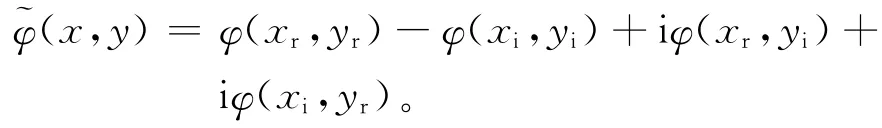
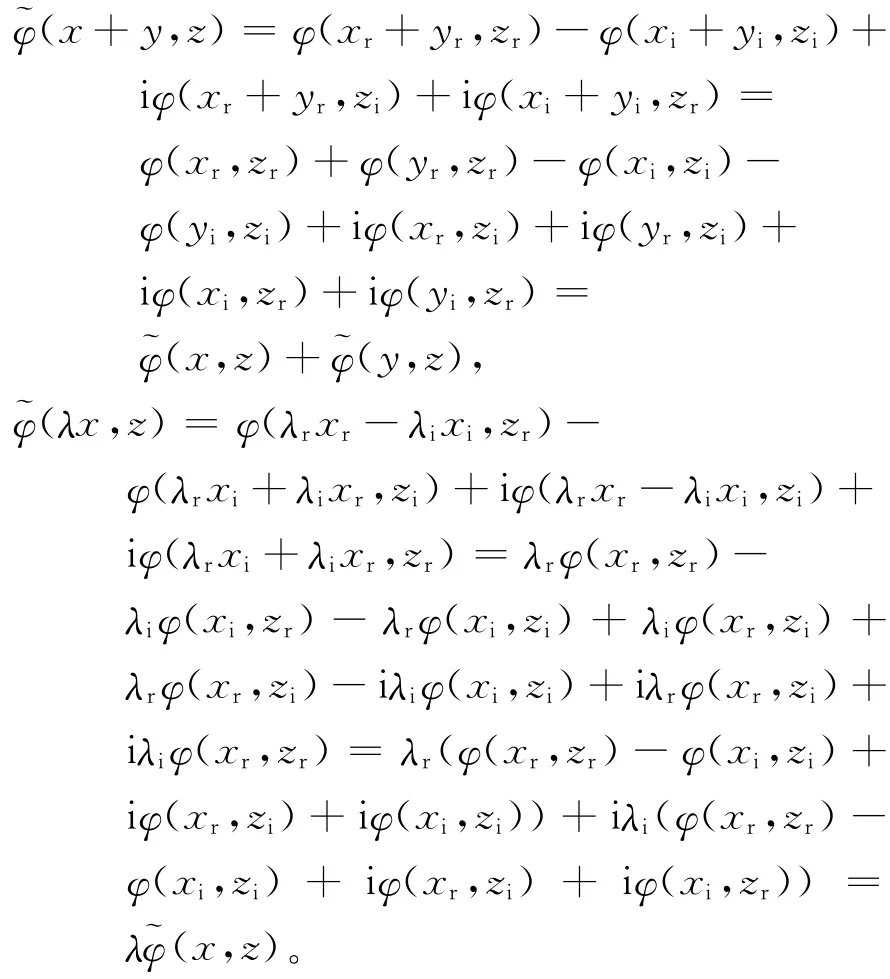
这说明~φ（·，z）是A上的线性映射。类似可得~φ（z，·）也是A上的线性映射。从而~φ是一个双线性映射。

由于（x◦y）r＝xr◦yr－xi◦yi且（x◦y）i＝xr◦yi+xi◦yi，则

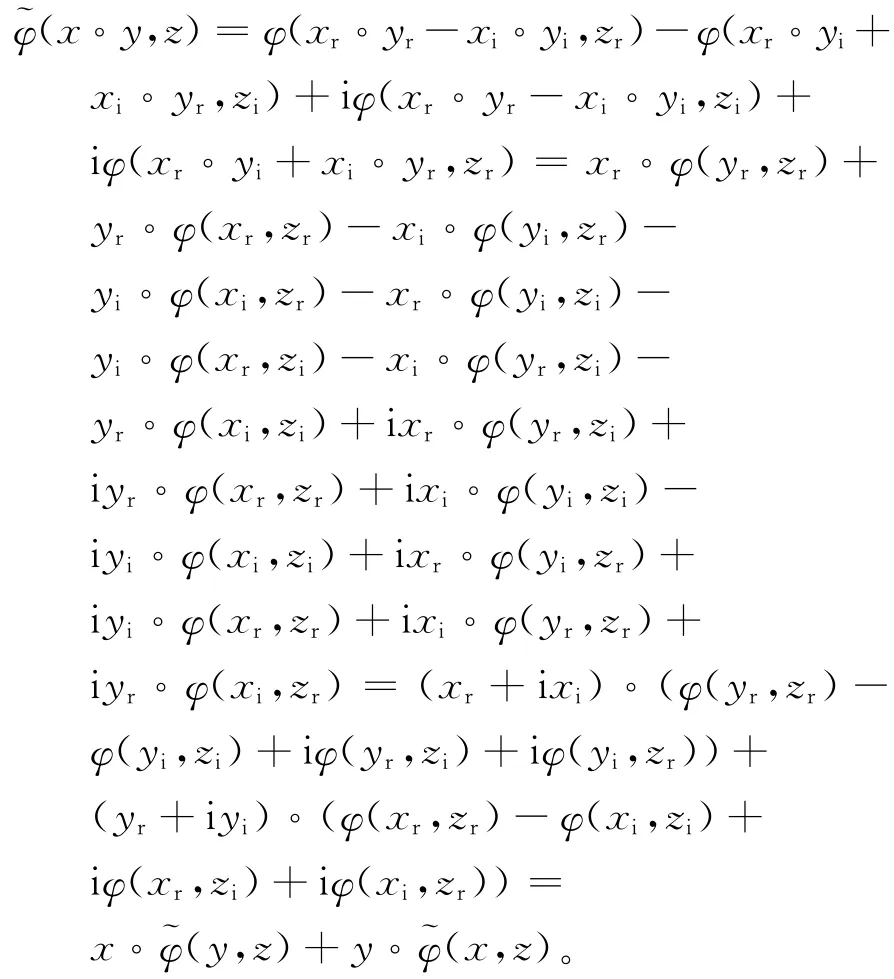
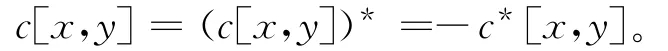
即（c+c＊）［x，y］＝0对任意的x、y∈As成立。由此，易验证：对任意的u、v∈A，有

由于A无非零中心理想，从而由（9）式可得c+c＊＝0。令a＝－i c，则a是Z（A）中的自伴算子且对任意的x、y∈As，有φ（x，y）＝i a［x，y］成立。证毕。

［1］Brešar M，Vukman J.On a generalization of the notion of centralizing mappings［J］.Proceedings of American Mathematical Society，1992，114：641－649.

［2］Brešar M.Commuting traces of biadditive mappings，commutativity－preserving mappings［J］.Transactions of American Mathematical Society，1993，335：525－546.

［3］Brešar M.Centralizing mappings and derivations in prime rings［J］.Journal of Algebra，1993，156：385－394.

［4］Sakai S.Derivations of W＊－algebras［J］.Annals of Mathematics，1966，83：273－279.

［5］Brešar M.Jordan derivations on semiprime rings［J］. Proceedings of American Mathematical Society，1988，104：1003－1006.

［6］Brešar M.On generalized biderivations and related maps［J］.Journal of Algebra，1995，172：764－786.

［7］Zhang J H，Feng S，Li H X，et al.Generalized biderivations of nest algebras［J］.Linear Algebra and its Applications，2006，418：225－233.

［8］Zhao Y，Wang D，Yao R.Biderivations of upper trian

gular matrix algebras over commutative rings［J］.Inter

national Journal of Game Theory，2009，18：473－478.［9］Benkovi cˇD.Biderivations of triangular algebras［J］.Linear Algebra and its Applications，2009，431：1587－1602.

［10］Du Y Q，Wang Y.Biderivations of generalized matrix algebras［J］.Linear Algebra and its Applications，2013，438：4483－4499.

［11］Brešar M.On certain pairs of functions of semiprime rings［J］.Proceedings of American Mathematical Society，1994，120：709－713.

〔责任编辑 宋轶文〕

Jordan biderivations on von Neumann algebras

WANG Lili，ZHANG Jianhua＊
（School of Mathematics and Information Science，Shaanxi Normal University，Xi'an 710119，Shaanxi，China）

It is proved that every Jordan biderivation of any von Neumann algebra without nonzero central ideals is an inner biderivation.As an application，it is obtained that the concrete structure of a Jordan biderivation on the real Jordan algebra of all self－adjoint operators of a von Neumann algebra without nonzero central ideals.

von Neumann algebra；biderivation；Jordan biderivation

47L30

O177.1

：A

1672－4291（2015）06－0017－04

10.15983／j.cnki.jsnu.2015.06.163

2014－12－09

国家自然科学基金（11371233，11471199）；教育部高等学校博士学科点专项科研基金（20110202110002）

王莉莉，女，硕士研究生，主要研究方向为算子代数。E－mail：1214566085＠qq.com

＊通信作者：张建华，男，教授，博士生导师。E－mail：jhzhang＠snnu.edu.cn