电商企业应急物流中的商品运输规划模型
2015-06-05范波峰杨毓玲
范波峰 杨毓玲
(1.西南科技大学环境与资源学院,四川 绵阳 621010; 2.西南交通大学交通运输与物流学院,四川 成都 610031)
电商企业应急物流中的商品运输规划模型
范波峰1,2杨毓玲1,2
(1.西南科技大学环境与资源学院,四川 绵阳 621010; 2.西南交通大学交通运输与物流学院,四川 成都 610031)
借鉴应急物流研究中运输优化的思路,采用最小费用最大流理论,建立了企业应急物流中商品运输模型,得出了在满足企业各配送点最小商品需求的前提下,以最低的运输费用将商品运送到各配送中心的运输方案,并给出了相应的求解方法。
最小费用最大流,企业应急物流,运输规划模型
企业应急物流是指企业为应对突发事件所引起的物流需求急剧变化而进行的快速响应活动。应急物流的研究[1],起源于战争、自然灾害以及突发公共事件等特殊状况下的物流活动设计,其研究主要集中在应急物资运输的优化、应急物流系统构建、应急物流系统能力评价以及突发事件对物流系统造成的影响等方面,这些方面的研究,除了应用于地区、国家等宏观层面,也可以为企业的应急物流运作提供有益的参考。
电子商务环境下,企业竞争加剧,广告、促销手段多样化、常态化,突发性、不确定性需求增加,往往导致企业物流成本上升,服务水平也难以达到客户要求[2]。为了节约成本、提高服务水平,许多大型电商开始整合自身物流资源,希望能通过有效控制,保证企业在需求急剧变化的时候能达到快速响应的目的。电商企业的应急物流需要考虑的重点是,如何在促销时段需求急剧增加的时候,保证满足各个配送点最小需求的情况下,以最小的运输成本将产品运送到各个配送点。
1 最小费用最大流理论[3]
1.1 相关概念
如果链的方向起点定为从vs到终点vt,则链上的弧被分为两种:一种弧的方向与链的方向一致,称这种弧为链的前向弧,前向弧的全体记为μ+;否则,称其为反向弧,记为μ-。
设f为一个可行流,μ是连接vs和vt的一条链,若μ满足下列条件,称之为流量可增链。
1)所有的正向弧,满足0≤fij 1.2 问题的描述 1.3 算法思路 网络最小费用最大流求解中,寻求f的最小费用的流量可增链即为关键问题。为此,可在原有网络D的基础上构造一个赋权有向图w(f),它的顶点就是原有网络D的顶点,且将D中每条弧(vi,vj)按照(vi,vj)和(vj,vi)的不同,分为两个方向相反的弧。 其中,w(f)中各弧的权值与f中弧的权值根据其方向的不同分别定义如下: 因此,只要在赋权有向图w(f)中,寻求从vs到vt的最短路即可。 2.1 企业应急物流模型 企业应急物资的运输要求在保证各配送中心预计最低需求的情况下,以最低的运输费用将尽可能多的产品从各供应商送到配送中心。 对于这样的应急物资运输问题,通常定义两个常量:fij以及bij。其中,fij是从i供应商运送到j配送中心产品的数量,bij是从i供应商运送单位产品到j配送中心所需要的费用。然后,以各应急企业供应商的物资储备量、供应商运输能力、各配送中心的最小产品需求量为约束条件,以产品运输量最大、总运输费用最小为目标函数,构造数学模型如下所示: s.t. (1) (2) (3) 0≤fij≤cij (4) 2.2 模型求解 如果有多个供应商和多个配送中心时,我们引进s点作为网络的起始点、t点作为网络的终止点,并做出如下规定: 1)从起始点s到第i个供应商的运输能力为i供应商的产品储备量,并且单位产品运输费用为0;2)从第j个配送中心到终点t点的产品运输能力为+∞,单位产品运输费用为0。 根据这样的规定,能够保持总运输费用不变,然后按照最小费用最大流算法求解模型。求解步骤[4]如下: 令: 企业的竞争导致网络促销越来越频繁,物流的快速性、低成本成为了电商企业竞争的焦点,利用最小费用最大流理论对产品的应急运输进行规划,可以有效提升企业的物流水平。在实际的企业运作中可以根据实际需求量的变化,随时得出相应的运输规划。 [1] 欧忠文,王会云,姜大力,等.应急物流[J].重庆大学学报, 2004,27(3):164-167. [2] 周丰婕.从国美熬夜惠看电子商务物流[J].物流工程与管理,2012,34(7):86-87. [3] 郭耀煌.运筹学原理与方法[M].成都:西南交通大学出版社,2000. [4] 邱 攀,胡圣能.网络流理论在地震救灾物资运输模型中的应用[J].物流科技,2010(3):13-14. Enterprise commodity transportation planning model of emergency logistics in E-commerce Fan Bofeng1,2Yang Yuling1,2 (1.SchoolofEnvironment&ResourceScience,SouthwestUniversityofScienceandTechnology,Mianyang621010,China;2.SchoolofTransportationandLogistics,SouthwestJiaotongUniversity,Chengdu610031,China) This pape learn from the method of transportation optimization in the emergency logistics research, use the theory minimum cost max-flow, establish the commodities transport model of enterprise emergency logistics, obtain the transportation scheme of commodities transported to the distribution center with the lowest transportation cost and meet the the minimum commodities demand of the distribution point, and put forward the solving method. minimum cost max-flow, enterprises emergency logistics, transportation planning model 2015-05-26 范波峰(1975- ),男,硕士,讲师; 杨毓玲(1974- ),女,硕士,讲师 1009-6825(2015)22-0238-02 TU984.191 A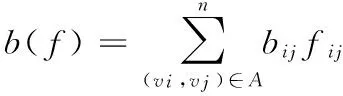
2 数学模型
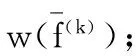


3 结语
