有衬砌条件下隧道地下水渗流场变化规律研究

董 翔

(都匀高速公路管理处，贵州 都匀 558000)

有衬砌条件下隧道地下水渗流场变化规律研究

董 翔

(都匀高速公路管理处，贵州 都匀 558000)

基于数值模拟方法，研究了隧道开挖后有衬砌支护情况下渗流场的变化及地下水位的变化情况，并分析了无衬砌条件下双孔隧道对渗流场的影响，得出了不同工况下孔隙水压力的变化情况及渗流场影响范围，并且得出了地下水位随时间的变化情况，可为隧道的设计、施工以及隧址区环境的保护提供参考。

隧道，地下水，渗流

0 引言

隧道工程的地下水问题伴随着隧道工程而产生，并始终伴随着隧道工程设计、施工和运营的整个过程[1]。在各种复杂或不良的地质条件中，地下水是影响隧道工程施工、运营和导致成本增加的主要原因之一[2，3]。在地下水丰富的地区，隧道渗漏水一直是一个具有广泛性、普遍性和危害性的难题[4-7]。因此，如何通过有效途径，弄清楚隧道施工引起的地下水渗流场变化情况，是隧道施工亟待解决的问题，对地下水进行经济有效的处理，是决定隧道工程成败的关键[8-10]。

1 数值模型的建立

对于地下水渗流方面的研究，不同学者在理论与实践中进行了较多的研究，而理论往往建立在一定的假设前提下，通常现场条件复杂，理论解答往往不能完全符合现场实际情况，而选用数值模拟方法对地下水渗流模型的研究相较于其他方法有着不可比拟的优越性。

1.1 FLAC3D

FLAC3D是二维的有限差分程序FLAC2D的拓展，能够进行土质、岩石和其他材料的三维结构受力特性模拟和塑性流动分析。该程序采用显式拉格朗日算法和混合—离散分区技术进行积分计算，可求解地质材料的高度非线性、孔隙介质的应力—渗流耦合、热—力耦合以及动力学等问题[11]。本文主要考虑隧道的开挖引起地下水渗流场的变化情况。FLAC3D中的渗流模式可以实现该功能。

1.2 数值模型建立

1)网格划分。目前常用到的经典渗流计算理论公式，其适用范围是无限大介质，参考前人对隧道开挖引起地下水变化的实地试验数据可知其影响半径可达数百米，故而建模需满足以下条件：a.尽量使模型的边界最大化；b.模型的计算应选用三维的六面体结构；c.数值计算中模拟的隧道开挖进深应与实际相符。

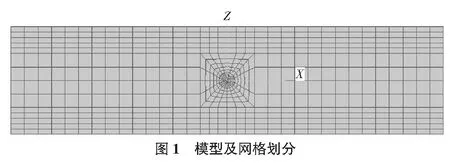
为了使数值模拟得到的结果合理、准确，在建模时应尽量满足上述所有条件。本文中采取的模型大小如图1所示。除建模外，网格划分对数值计算的准确性有着一定的影响。在单元形状确定之后，当单元网格划分越细时，位移近似解将收敛于精确解。增加网格数量和密度，计算精度一般也会随之提高。但是，如果盲目地增加网格数量，将会大大增加单元网格划分时间及求解方程时间。有时还会因计算的累积误差反而降低计算精度。本文考虑到能准确监测到隧道开挖对周围岩体渗流场影响的动态过程，对上边界处单元竖向尺寸进行了一定的细化，本着既能控制计算时间，又能得到精确的结果为原则划分网格，如图1所示，模型中共有3 360个单元。

2)参数选取。本文中所选取的材料参数如表1所示。

表1 力学模型参数

2 数值模拟结果分析

分别就几种不同的工况进行模拟，对比分析得出，不同工况下隧道施工对其周围岩体渗流场的影响情况。

施作衬砌情况下地下水位动态变化。在模型中设置水流流动时间为3 d，围岩渗透系数为10-8m/s，孔隙率为0.25，隧道开挖半径5 m，衬砌厚度为15 cm，渗透系数为10-12m/s，对比分析有无衬砌对孔隙水压力分布的影响。

从图2，图3可以看到隧道孔隙水压力在开挖后3 d内动态变化过程，并可定性地得出，在隧道施工过程中及时施加衬砌，将有利于减缓围岩孔隙水压力的降低程度，减小隧道施工引起的降水范围。

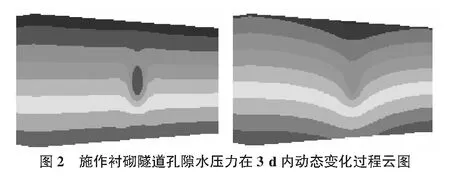
为了能定量分析有无衬砌对围岩孔隙水压力的影响，我们对监测点最终的孔隙水压力进行处理分析，如图4所示。

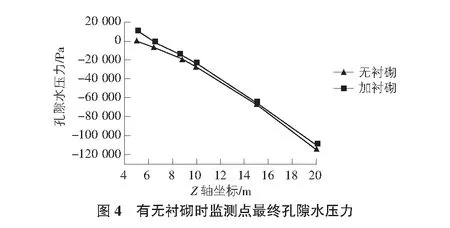
从图4中我们可以看到，施加衬砌将有效减小围岩孔隙水压力的变化，并且对隧道周围的孔隙水压影响最为显著。但是为了控制变量，我们将流体流动时间设置为3 d，这将使得隧道上部的水流尽，所以，施加衬砌与无衬砌工况下对3 d后离隧道较远处的孔隙水压影响不大。

3 结语

采用FLAC3D数值模拟软件对无衬砌及有衬砌支护情况下地下水位变化趋势进行了研究，取得了如下研究成果：

1)分析了隧道排水后孔隙水压力变化趋势及变化规律。隧道开挖后，隧道围岩孔隙水压力减小，随时间增长，渗流影响范围逐渐扩大。

2)通过对浸润线的描绘，可得出隧道排水情况下任意时刻地下水位降深，可为隧道的排水设计以及对隧址区植被生态的保护提供依据。

3)通过对双孔隧道的分析得出，双孔隧道由于排水量大于单孔隧道，其对渗流场的影响更大，而地下水位下降速度也较快，在双孔隧道施工及设计过程中，应该考虑叠加效应。

[1] 薛禹群.中国地下水数值模拟的现状与展望[J].高校地质学报,2010(1):1-6.

[2] 陆 乐,吴吉春.地下水数值模拟不确定性的贝叶斯分析[J].水利学报,2010(3):264-271.

[3] 卢文喜.地下水运动数值模拟过程中边界条件问题探讨[J].水利学报,2003(3):33-36.

[4] 徐 军,杨本水,宣以琼.地下水对水下隧道的不良影响分析及应对措施[A].地下交通工程与工程安全——第五届中国国际隧道工程研讨会文集[C].2011.

[5] 屈建军,李建林,刘 杰,等.考虑地下水作用的渗流场与应力场耦合分析[J].水电能源科学,2010(1):50-53.

[6] 罗富荣,刘赪炜,韩 煊.地下水水位上升对地铁隧道结构的影响分析[J].中国铁道科学,2011(1):81-85.

[7] 沈媛媛,蒋云钟,雷晓辉,等.地下水数值模拟中人为边界的处理方法研究[J].水文地质工程地质,2008(6):12-15.

[8] 李玉杰,王连国,陆银龙,等.地下水对巷道围岩稳定性影响的数值模拟[J].徐州工程学院学报(自然科学版),2011(1):34-39.

[9] 张亦龙.富水隧道地下水预测及力学特性分析[D].成都：西南交通大学,2013.

[10] 周跃峰,谭国焕,甄伟文,等.非饱和渗流分析在 FLAC3D中的实现和应用[J].长江科学院院报,2013,30(2):57-61.

[11] 高素荷.网格划分密度与有限元求解精度研究[J].重工科技,2007(1):12-15.

On change laws for the underground seepage field of tunnels under lining condition

Dong Xiang

(DuyunExpresswayAdministrativeOffice,Duyun558000,China)

Based on the numeric simulation method, the paper researches the changes of the seepage fields under the lining support after the tunnel excavation and alteration of the underground water level, analyzes the influence of the double-hole tunnel under the lining condition, concludes the changes of the pore water pressure under different conditions, and achieves the changes of the underground water level along with the time, so as to provide some reference for the design of tunnels, construction and protection of the tunnel address areas.

tunnel, underground water, seepage

2015-05-29

董 翔(1977- )，男，硕士

1009-6825(2015)22-0166-03

U453.61

A