桥面不平整度对桥梁冲击系数的影响研究
2015-06-05訾建峰
訾 建 峰
(天津市市政公路工程质量监督站,天津 300384)
桥面不平整度对桥梁冲击系数的影响研究
訾 建 峰
(天津市市政公路工程质量监督站,天津 300384)
采用有限元方法,研究了桥面不平整度对不同跨度及宽度简支梁桥冲击系数的影响,结果表明,桥面不平整对桥梁冲击系数影响显著,且与桥梁的宽跨比有关;当宽跨比小于1.0,桥面不平整时冲击系数随着桥梁宽跨比变化明显,而当宽跨比在2.0~3.0之间时,冲击系数的变化趋势减缓,相对稳定,宽跨比的影响可以忽略。
冲击系数,不平整度,宽跨比,动响应
0 引言
在现行的各国桥梁设计规范当中,冲击系数的取值大多是随加载长度或跨度的增加为递减函数的运算公式。然而,这一公式并不能很好的综合反映各种因素对冲击系数的影响。因此,国内外仍在对于这一研究问题进行大量的现场实验以及理论研究,希望能得到对冲击系数的合理表达公式[1-4]。我国的桥梁规范中规定桥梁的冲击系数只和桥梁的结构频率相关[5,6],这是不符合实际安全性的。特别是对于老旧桥梁,当桥上荷载因桥面平整度恶化对桥梁的冲击作用将更加突出,对桥梁的承载能力和结构安全则影响更大。因此,桥面的平整度对冲击系数的影响研究不容忽视。
为此,本文采用有限元的方法,建立标准跨径的桥梁模型,同时设置桥面平整度,分别进行静力和动力分析。通过对比桥梁结构的跨中静挠度和动挠度,建立桥面平整度对桥梁冲击系数的影响规律,为桥梁的结构设计提供理论依据。
1 有限元模型建立
1.1 参数设置
根据《公路桥梁通用设计规范》中规定的行车道宽度设计所需研究的钢筋混凝土桥梁的尺寸,选取矩形梁截面,利用有限元软件ANSYS分别建立10 m,12 m,14 m,16 m,18 m和20 m跨径、对应不同宽跨比的钢筋混凝土简支梁模型。所有钢筋混凝土简支梁桥模型的混凝土材料强度取C30,弹性模量Ec=3.0e10 N/m2,泊松比0.2,密度为2 500 kN/m3。采用Solid65单元模拟混凝土材料,钢筋采用HRB335,钢筋配筋率采用0.4%。
1.2 动荷载的施加
选用击振的方法对行车道板跨中位置施加动荷载,为了模拟车辆荷载作用下桥梁的振动响应,模型中采用质量块对简支梁桥施加振动荷载,并对简支梁桥模型进行瞬态分析,求解在动荷载作用下的跨中最大位移。
2 桥面平顺时简支梁桥动态响应分析
采用上述模型,按照动荷载的施加方法,计算并提取跨中节点的位移时程响应。图1给出了不同跨径简支梁桥随宽跨比的最大动挠度曲线。可以看出,对于相同跨径桥梁,随着宽跨比的增加动力响应越小。当宽跨比小于1.4时,动力响应随着宽跨比的减小,动挠度下降明显,而当宽跨比大于1.4时动挠度随宽跨比的变化趋缓。

3 考虑桥面不平整度为5 cm时简支梁桥动态响应分析
将击振块高度改为5 cm后,对结构动力响应进行求解,读取跨中最大挠度值。图2给出了根据桥面不平顺时钢筋混凝土简支梁桥动力挠度图。
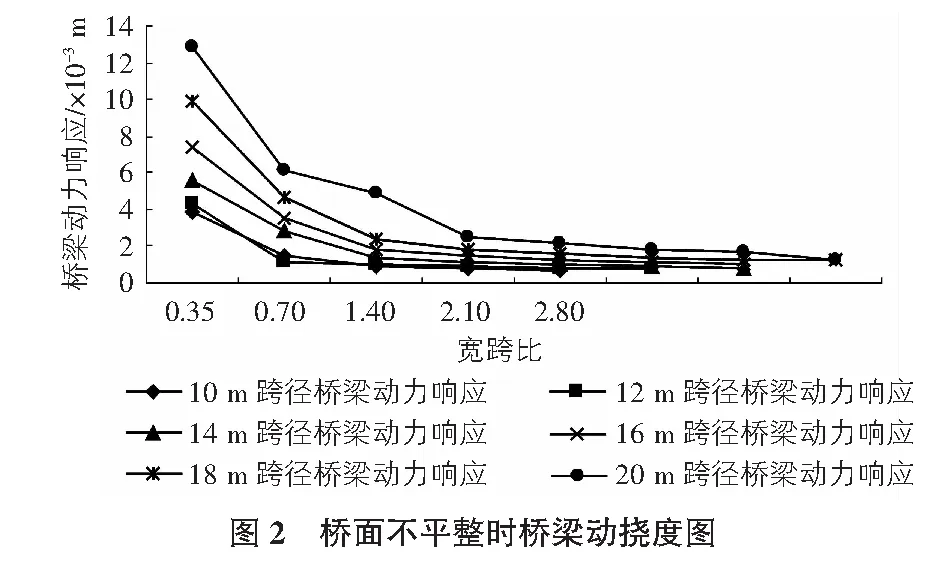
桥面不平整情况下桥梁的动力响应值明显大于桥梁平整时的挠度值。相同宽跨比的条件下,跨度越大挠度越大。同一跨径下桥梁挠度随宽跨比增加而减小。宽跨比小于1.4时,桥梁的动力响应值变化剧烈,宽跨比大于1.4时,桥梁动力响应随宽跨比增大变化趋缓,这与桥面平顺时桥梁的动响应规律相同。
4 冲击系数分析
4.1 规范冲击系数的计算
使用ANSYS中的模态分析对所建钢筋混凝土简支梁桥的模型进行模态分析,计算结构的基本频率。进一步,根据规范中冲击系数的计算公式[6]计算出桥梁规范中的冲击系数(如表1所示)。

表1 规范冲击系数
4.2 模型冲击系数的计算
首先,采用上述钢筋混凝土简支梁桥模型进行静力分析,计算简支梁桥在跨中施加集中荷载作用时,结构产生的最大静位移。图3给出了钢筋混凝土简支梁桥的静挠度曲线。依据跨中静挠度和动挠度结果,根据式(1)确定桥梁模型的冲击系数,并与基于规范确定的桥梁冲击系数进行比较。

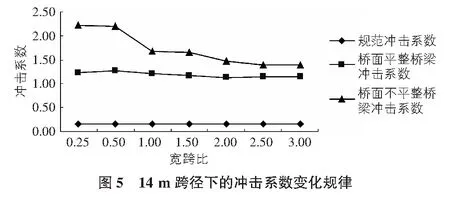
图4~图7分别给出了跨径10 m,14 m,16 m和18 m桥梁在考虑桥面平顺以及不平整状态下的冲击系数与规范计算值随宽跨比的变化曲线。
1+μ=yd/yj
(1)
其中,yj为最大静力效应值;yd为最大动力效应值。
从图4~图7可以看出,桥跨不变的情况下,规范中规定的冲击系数是不变的,而基于模型确定的桥梁冲击系数随着宽跨比增大而减小。此外,桥面不平整对桥梁冲击系数影响显著,明显高于桥面平顺状态和基于规范确定的冲击系数。当宽跨比小于1,桥面不平整时冲击系数随着桥梁宽跨比变化明显,而当宽跨比在2~3之间时,冲击系数的变化趋势减缓,宽跨比的影响可以忽略。



5 结语
基于有限元方法研究桥面不平整度对不同跨度及宽度简支梁桥冲击系数的影响。结果表明,桥面不平整对桥梁冲击系数影响显著,且与桥梁的宽跨比有关。此外,桥面不平整时的冲击系数大于基于规范的冲击系数计算值,因此,依据规范不考虑桥面不平整度确定冲击系数是不安全的。
[1] 李玉良.公路桥梁冲击系数随机变量的概率分布及冲击系数谱[J].公路,1996(3):1-6.
[2] 李小珍.公路桥梁与车辆耦合振动研究现状与发展趋势[J].工程力学,2008(25):230-240.
[3] 宋一凡,贺拴海.公路桥梁冲击系数的影响因素分析[J].桥梁,2001(2):47-49.
[4] 杨艳娟.公路桥梁冲击系数的理论分析与探讨[J].桥梁,2009(9):49-50.
[5] 李亚东.桥梁工程概论[M].第2版.成都:西南交通大学出版社,2006.
[6] JTG D60—2004,公路桥涵设计通用规范[S].
Research on the effect of roughness on the bridge impact coefficient
Zi Jianfeng
(TianjinMunicipalRoadEngineeringQualitySurveillance,Tianjin300384,China)
The bridge impact coefficient influenced by roughness of bridge floor based on finite element method. Results indicate that roughness prominently influenced on the bridge impact coefficient. It relates to the bridge width-span ratio. The impact coefficient changed with width-span ratio obviously as width-span ratio less than 1.0. While the impact coefficient changed slow down as width-span ratio between 2.0 and 3.0, and the influence of bridge width-span ratio on the impact coefficient could be ignore.
impact coefficient, roughness, width-span ratio, dynamic response
2015-04-03
訾建峰(1977- ),男,硕士,高级工程师
1009-6825(2015)17-0152-03
U445.71
A
