基于等效电流模型的永磁多自由度电机位置检测方法的研究*

李 争， 郭曼洁， 马 骏

(河北科技大学 电气工程学院，河北 石家庄 050018)

基于等效电流模型的永磁多自由度电机位置检测方法的研究*

李 争， 郭曼洁， 马 骏

(河北科技大学 电气工程学院，河北 石家庄 050018)

提出了一种新的永磁体磁场建模方法及三自由度电机转子的位置检测方法。根据分子环流假说和毕奥-萨伐尔定律将圆鼓形永磁体等效为相应的电流模型，从而得到永磁体的静磁场，再经过一定的坐标变换，将静磁场变为运动的旋转磁场，并通过一组霍尔传感器获得永磁体的实时位置。通过对永磁体的磁场建模进行仿真验证，并且与多项式近似法进行误差的对比，从而验证方法的可靠性。

永磁体； 多自由度； 位置检测； 等效电流模型

0 引 言

永磁转子偏转式三自由度电机是一种利用转子上的永磁体和定子上通电线圈的相互作用，使转子产生三自由度运动的永磁电机。该电机主要应用于航空、航天、机器人和仿生学等领域，其克服了传统电机的多球轴承支撑、摩擦力大、运动方向单一等缺点，具有很高的研究价值[1-4]。

转子的位置检测是研究多自由度电机的关键技术之一[5-8]。美国约翰霍普金斯大学Gregory S Chirikjian、David Stein等人用光电传感器来检测球形表面的黑白颜色信号；Harry Garner和Kok-Meng Lee等人提出视觉传感器系统，检测转子表面偏移量；Kok-Meng Lee等人提出永磁体的分布式多极模型(Diamond Mortensen Pissarides, DMP)，用两组霍尔传感器获取磁场信号[10-12]。本文在深入研究DMP模型的基础上，从新的角度提出转子位置检测的新方法，即等效电流模型[15-17]。对圆鼓形永磁体进行等效电流模型建模，建立空间磁感应强度B与旋转角度(α、β)之间的关系，反解方程组来确定永磁体的位置角度。最后将仿真结果与DMP模型方法进行对比分析，进一步通过具体的试验数据，对所讨论的检测方法进行验证。验证结果证明了本文模型建立的正确性，并为此类电机的进一步研究提供理论参考。

1 永磁转子偏转式三自由度电机的结构模型

本文研究的永磁转子偏转式三自由度电机结构模型如图1所示。电机定子分为上下两层，电机高度为17.5mm，上下两层定子间距为 5.5mm，外径为90mm，内径为78mm，磁极由带铁心线圈通电构成，磁轭高度和厚度均为6mm；电机转子由稀土永磁材料NdFeB制成，形状为圆鼓形，转子半径为15.5mm，保持定转子之间气隙为0.5mm。定转子磁极数量分别为6极、4极配合。

图1 永磁转子偏转式三自由度电机结构模型

2 电机转子建模

关于磁介质的磁化理论有磁荷观点和分子电流观点两种不同的观点。前者用一对磁偶极子来解释永磁材料的磁化强度，广泛应用于形状简单的永磁体中。后者用等效电流的概念取代了磁性材料的边界效应。在目前所研究的三自由度运动电机中，计算磁场的方法大多数为磁荷观点(如DMP模型方法)，而很少采用分子电流观点。

2.1 圆鼓形永磁体的分子环流模型

分子电流观点即安培分子环流假说。根据毕奥-萨伐尔定律，定义载流细导线回路中的电流元Idl在空间任一点P(x,y,z)产生的磁感应强度为

(1)

式中:r′——源点(x0，y0，z0)矢径；

r——场点P(x,y,z)矢径。

将永磁转子偏转式三自由度电机的圆鼓形转子示意图置于笛卡尔坐标系中。将圆鼓形永磁体的四部分分别编号1、2、3、4，相对的两部分永磁体分别沿z轴相反方向均匀磁化达到饱和状态，从而产生图2所示的电流方向。由分子环流假说可知： 磁体外部空间任一点的磁场由永磁体表面闭合的电流环ABCDA所激发。设环路内面磁化电流密度为Js(A/m)。

图2 圆鼓形永磁体的电流等效模型

以第一部分永磁体为例，取厚度为dz0的薄层电流环ABCDA，其电流强度为I=Jsdz0，则总电流环在P处产生的总磁场为

(2)

其中，dBx、dBy、dBz分别是强度为I的薄层电流环ABCDA在P处产生的磁场在x、y、z方向的分量。它们又分别由4个电流段，AB段、BC段、CD段、DA段的叠加作用而成。

BC段在P产生的磁场：

(3)

同理得到DA段、AB段和CD段的dBix、dBiy和dBiz(i=2,3,4)。为表述简单，记:

(4)

其中，ψi是以φ1、φ2、φ3为自变量的函数记号。故:

dBx=dB1x+dB2x+dB3x+dB4x=

(5)

第一块永磁体的空间总磁场为

(6)

在z方向上进行积分，最终得到整个永磁体在P点产生的磁场：

(7)

式中：r——永磁体内径；

R——永磁体外径；

h——永磁体高度。

为表述简单，将式(7)记为B=KB′。

得到永磁转子电流等效模型的关键是求得唯一的未知数Js，即式(7)中的常量K。用高斯计测量永磁体的磁场，并将数据记录于表1。

表1 计算K值

2.2 旋转磁场

上文所求得的空间某一点的磁场是在永磁体的静磁场，而永磁转子要实现三个自由度上的旋转运动，所以要得到永磁体旋转的运动磁场，即完成固定坐标系与旋转坐标系之间的转换。坐标变换式为

B(X,Y,Z)=C(α,β,γ)·B(x,y,z)

(8)

式中:C——坐标变换矩阵,C=(α,β,γ);

α、β、γ——描述转子坐标系xyz的欧拉角。

偏移角、倾斜角和自转角的定义如图3所示。

图3 偏移角、倾斜角和自转角的定义

式(6)即变为

Z(α,β)-z0)dy0+0-

y0,Z(α,β)-z0)dx0-

(9)

同理可得其他磁场的变换式。经过坐标变换的式(7)可记作:

(10)

3 基于等效电流模型的转子位置检测方法

3.1 位置检测方法

本文采用两组霍尔传感器作为磁场信息采集的工具。为了得到较为精确的测量数据，四个线性霍尔元件分别放置在固定坐标系的X轴和Y轴，分别距永磁体1.5cm，传感器的位置坐标如图4所示。两组分别位于同一坐标轴的传感器分别用于对两个偏转角度的测量。

图4 传感器的放置位置

对于每组传感器来说，可得以下两个方程：

(11)

(12)

其中： 下标Pm、Pn表示第m、n个传感器；式(11)中m=1,3，式(12)中n=2,4。

(13)

其中，Q1、Q2分别为两组传感器的2×2权重矩阵，由于每对沿X-轴的传感器与沿Y-轴是相互独立的，因此权重矩阵可以选择为

(14)

3.2 计算结果分析

用MATLAB仿真软件对永磁体的磁场进行仿真建模。图5为等效电流模型的第一部分永磁体的磁感应强度B(Z)沿Z轴方向的变化。可以看出，由永磁体下端沿Z轴正方向，磁感应强度逐渐增大，与前文所假设的电流产生的磁场变化相一致。

图5 第一块永磁体中的磁密

图6为模拟永磁体自转的仿真图。从图6中可以明显的看出，图形近似于正弦波，且在一个周期2π中有2个波峰和2个波谷。与圆鼓形永磁体的4个磁极相对应。

图6 永磁体自传仿真图

对传感器P1处的磁场进行仿真模拟。图7给出了永磁体绕X轴旋转的磁场BX在传感器P1(0,25,15) 处关于角度(α,β)的分析解，(α,β)的范围均为±pi/9。

图7 倾斜角为±pi/9时的等效电流模型

3.3 结果对比

为进一步验证模型的正确性，这里将圆鼓形永磁体电流等效模型与文献[18]中的多项式逼近法进行误差的对比。图8～图10分别为永磁体的电流等效模型与n=1，2，3时的多项式进行误差的对比。

图8 与n=1的误差

图9 与n=2的误差

图10 与n=3的误差

由图8～图10可知，随着多项式逼近法中阶数n的增加，永磁体等效电流模型与之的误差逐渐减小。图8所示为一阶误差图，由图8可以看出，磁场的总体误差较大，约5×10-3；图9和图10分别为二阶误差图和三阶误差图，从图9、图10中可以看出，总体误差较小，仅在永磁体旋转经过0°附近时误差较大，最大二阶误差约为4×10-3，三阶误差约为3×10-3。

3.4 试验验证

为验证本文所研究算法的可用性，建立永磁体位置检测系统，如图11所示。包括霍尔传感器、下位机和上位机。将永磁体固定于支架上，距其上方1.5cm处对称地放置4个线性霍尔传感器；下位机使用CEPARK STM32F103RCT6开发板进行数据采集及数据处理；而Visual Basic因其丰富的控件、可实现各种功能作为上位机界面编写的首选软件，并将本文讨论的永磁体的等效电流模型写入上位机。

图11 永磁体位置检测系统

在X轴方向固定永磁体，并在一定角度范围内绕Y轴依次旋转，将得到如图12的上位机界面数据，采样数据依次列于表格中。α角由于误差的存在，在0°上下晃动；β角成正弦曲线波动。并且，在界面的右侧，虚拟永磁体的倾角将随试验中永磁体的倾斜角的变化而变化。

图12 上位机界面

用自动检测系统和高斯计测量法分别对永磁体进行角度的测量，通过对比采样数据的误差，来验证此算法是否具有可行性。旋转永磁体，这里对永磁体旋转半个周期，每旋转一定角度，直接测出此时永磁体的偏转角度，并且在自动检测装置上多次采样几组数据，求出此时偏转角度的平均值。将两种采样数据的结果进行对比，绘出误差曲线，如图13所示。

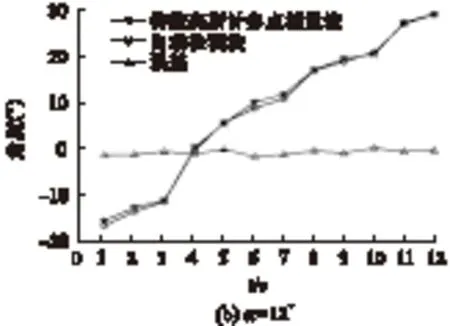
图13 两种检测方法的测量误差对比

通过上面自动检测装置与传统的测量方法结果的对比可以看出，两种方法的误差在可接受的范围内。这就说明，等效电流模型用于永磁体的位置检测是具有一定的可行性的。

4 结 语

本文在介绍一种新型永磁转子偏转式三自由度电机的基础上，对其转子位置检测方法进行了理论分析。针对圆鼓形永磁转子，提出了一种新的永磁体建模方法，即等效电流模型。通过对永磁体等效电流模型进行仿真建模，并与多项式逼近法进行对比分析，为永磁转子偏转式三自由度电机的进一步研究提供了理论参考。为了验证本算法的可行性，本文最后介绍了用两种方法对现有的阶梯型永磁体进行的对比试验。通过具体的试验数据，有力地说明了本文讨论的方法可以可靠地用于永磁转子位置的检测。

[1] 李争，王咏涛，葛荣亮，等.永磁球形多自由度电机研究进展综述[J].微电机,2011，44(9): 66-70.

[2] 李争，孙克军，王群京，等.一种多自由度电机三维磁场分析及永磁体设计[J].电机与控制学报，2012,16(7): 65-71.

[3] 李争，郭智虎，张玥.新型永磁转子偏转式三自由度电机磁场特性分析[J].河北科技大学学报，2012,33(5): 422- 428.

[4] 王张合，曾励，姜明明.多自由度球形关节电动机的发展现状及研究方向[J].现代制造工程,2010，33(1): 145-149.

[5] 王群京，钱喆，郭中醒.三维球形电动机位置检测的研究与发展[J].微特电机，2009，37(12): 65-69.

[6] 过希文，王群京，李国丽.多自由度永磁球形电动机控制策略的研究与发展[J].微特电机,2011,39(2): 72-79.

[7] LIM C K,CHEN I M, YAN L, et al. A novel approach for positional sensing of a spherical geometry[J]. Sensors and Actuators A: Physical, 2011，168(2): 328-334.

[8] TSAI M C， YANG C H. A Flux-Density-Based Electromagnetic Servo System for Real-Time Magnetic Servoing/Tracking[J]. IEEE/Asme Transactions on Mechatronics, 2008,13(2): 249-256.

[9] LIM C K, YONG C, CHEN I M, et al. An alternative approach in sensing simultaneous 3-DOF motions[C]∥The 2006 IEEE international confer-ence on Automatic Science and Engineering Shang-hai, 2006: 588-593.

[10] 王群京，钱喆，李争，等.基于机器视觉的永磁球形步进电动机转子位置检测方法[J].中国电机工程学报，2008,28(36): 73-79.

[11] LEE K M, SON H S. Distributed multipole model for design of permanent-magnet-based actuators[J]. IEEE Transactions on Magnetics, 2007(10): 3904-3913.

[12] SON H S, LEE K M. Distributed multipole models for design and control of PM actuators and sensors[J]. IEEE/Asme Transactions on Mechatronics, 2008,13(2): 228-238.

[13] 汤双清，陈习坤，唐波.永磁体空间磁场的分析计算及其在永磁磁力轴承中的应用[J].大学物理,2005,24(3): 32-36.

[14] 张志艳，马宏忠，陈诚，等.改进磁偶极子模型在永磁电机场中的应用[J].微电机，2012,45(8): 22-71.

[15] 赵长海.介质磁化理论中两种等效观点的探索[J].陕西师范大学继续教育学报,2004,21(3): 106-107.

[16] 苟晓凡，杨勇，郑晓静.矩形永磁体磁场分布的解析表达式[J].应用数学和力学,2004,25(3): 271-278.

[17] 刘宏娟.矩形永磁体三维磁场空间分布研究[D].北京： 北京工业大学,2006.

[18] 李争，王欣欣，张玥.基于分布式多极磁场模型的永磁多自由度电机位置检测方法研究[J].微电机,2014,47(3): 37- 42.

Magnetic Field and Position Detection of PM Actuators Based on Equivalent Current Model

LIZheng,GUOManjie，MAJun

(College of Electrical Engineering, Hebei University of Science and Technology,Shijiazhuang 050018, China)

The structure model and the operation principle of a new type of PM deflection type three-degree-of-freedom (3-DOF) motors were introduced. A new modeling method of the magnetic field of permanent magnet was proposed and the rotor position detection method was referred. The equivalent current model of the mentioned PM could be obtained based on Ampere’s molecular current hypothesis and the Biot-Savart’s law. A set of Hall sensors would be used here to get the magnetic field information. The modeling method of the magnetic field has been verified by simulation and error comparison with the Polynomial Approximation has been conducted. Simulation results and comparison showed the feasibility of this new method for further research.

permanent magnet; 3-DOF; position detection; equivalent current model

国家自然科学基金项目(51107031)；河北省自然科学基金项目(E2014208134)

李 争

TM 306

A

1673-6540(2015)05-0042-06

2014-09-01