基于行列式随机循环的压缩感知测量矩阵研究

魏从静，唐加山

(南京邮电大学 a.通信与信息工程学院；b.理学院，江苏 南京 210023)

基于行列式随机循环的压缩感知测量矩阵研究

魏从静a，唐加山b

(南京邮电大学 a.通信与信息工程学院；b.理学院，江苏 南京 210023)

压缩感知理论，从信号的自身特性出发，通过变换作用域和线性投影实现对信号的采样和压缩。测量矩阵是该理论中获得的最优测量，实现精确重构的关键。本文在介绍常用测量矩阵的基础上，重点研究了结构化测量矩阵。鉴于测量矩阵设计的最重要的原则是降低矩阵元素间的相干性，借鉴循环矩阵和广义轮换矩阵的优点，提出了采用均匀随机数对结构化测量矩阵进行随机循环的构造方法。仿真实验表明新矩阵在信号重建上具有更好的性能。

压缩感知；测量矩阵；托普利兹矩阵；随机循环

信号采样架起了模拟信源和数字信息之间的桥梁，传统的信号采样方法以香农定理为基础。然而，随着处理信号的带宽和数据量越来越大，这种方式使有限带宽假设的采样方法受到了巨大挑战。压缩感知[1-2](Compressed Sensing，CS)理论基于信号在特定变换域下是稀疏的或可压缩的前提，将高维信号通过线性测量映射到一个低维空间，实现对数据采样的同时进行压缩，并最终通过求解组合优化问题从这些少量的低维信号中以高概率恢复出原始信号。

CS理论主要包括信号稀疏变换、测量矩阵设计和重构算法三个方面。测量矩阵的设计决定了此理论能否成功实现以及是否适合应用于实际。在各类测量矩阵中，Toeplitz结构矩阵由于存储和计算的复杂度低，而且硬件实现容易，使得它们具有更为广泛的实际应用，也是测量矩阵设计研究的重点。如近年提出的在特定条件下的基于粒子群优化算法的Toeplitz结构矩阵改进方法[3]，以及在需要更多的测量值的代价下，以分段Toeplitz矩阵进行测量[4]。本文在研究Toeplitz矩阵[5]和广义轮换矩阵[6]的基础上，引入随机循环的思想，提出对Toeplitz结构矩阵的改进方法。新矩阵与原矩阵相比，在相同的观测值时，对原信号具有更好的重构性能。

1 压缩感知理论框架

CS理论从信号的内部结构出发，指出信号的采样频率不再取决于信号的带宽，而依赖于两个重要的特征：稀疏性和不相干性。

考虑一实值的有限长一维离散时间信号f，一维空间的N个离散采样点可以看作为RN空间N×1维列向量。信号f本身可能是稀疏的或可压缩的。然而，更一般的情况是信号f在某个适当的基或字典中有一个稀疏的展开式。例如，f可以表示成RN空间的一组标准正交基的线性组合

(1)

式中：Ψ为N×N维矩阵；向量Θ则是信号f在变换基Ψ下的系数，而变换后Θ的N个系数满足稀疏性或可压缩性。

CS理论的测量过程是用与系数变换基Ψ不相干的M×N(M≤N)维测量矩阵Φ去获得M个观测值，该过程是非自适应的。线性测量过程可以写成如下形式：Y=Φf=ΦΨΘ=AcsΘ。变换基Ψ和测量矩阵Φ的互相干程度越小，重构信号所需的测量值越少，成功重构信号的概率就越高[7]。

信号的重构是指由M个观测值去重构长度为N的稀疏信号过程。可以通过求解如下最优化问题得到满足条件的稀疏解

在种植小麦时期，应降低病虫害基础。在防止病虫害时，可实行有效的防治手段，有效结合农业和化学防治，进行精耕细作和晚播，进而增强麦苗的抵抗力，同时降低麦苗发病率。可以使用药剂搅拌、包衣等方法，还应做好土壤处理，对于不同的病虫害应使用对应的药剂做包衣。比如纹枯病，应使用氟环唑或者是三唑酮杀毒及，然后喷洒水在茎部，定期喷药，不仅能够有效治疗病症，还可以防治其他疾病，或者可以使用除草、深耕的方法防治。当出现麦穗蚜病症时，在使用快杀灵乳油三百到五百毫升，再喷洒水，使病虫害的得到有效防控。

(2)

然而该问题在现实中是个NP-hard问题。如果感知矩阵Acs满足受限等距性(Restricted Isometry Property， RIP)性质[8]，式(2)等价于求解如下l2范数

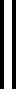
(3)

求解式(3)的计算可行性方法有：基于贪婪类的算法和基于凸优化的算法[9]。

2 压缩感知测量矩阵

2.1 压缩感知测量矩阵介绍

高斯随机矩阵、贝努利随机矩阵以及部分傅里叶矩阵都满足UUP(Uniform Uncertainty Principle)条件，从而可以高概率的重构原信号[10]。然而在实际应用中，高斯随机矩阵、贝努利随机矩阵的完全随机性给矩阵的存储，硬件的设计等都带来了困难，同时需要大量的独立重复实验来消除矩阵的随机性带来的仿真结果的不确定性。部分傅里叶矩阵只与时域稀疏信号不相干，然而时域稀疏的信号往往极少存在。

Toeplitz矩阵和循环矩阵[5]是其元素独立的抽取于满足特定概率分布的结构化随机矩阵。Toeplitz矩阵的具体构造方法是：先生成一个M+N-1维行向量μ=(μ1,μ2，…，μN，…，μM+N-1)，其中μi服从式(4)的概率分布

(4)

然后通过循环移位生成形如式(5)的M×N维矩阵

(5)

2.2 基于行列式随机循环的测量矩阵设计

形如式(5)的测量矩阵在实际应用中与其他类矩阵相比具有以下优点：1)仅需O(N)个独立随机变量，减小了存储量；2)矩阵的特殊结构使得矩阵相乘可以借助快速傅里叶变换实现；3)循环矩阵在某些特殊的应用能自然产生。因此，本文将对此类结构化随机矩阵做进一步研究并加以改进，使其在信号重建上具有更好的性能。

测量矩阵需要满足UUP条件，然而直接验证测量矩阵满足UUP条件通常是困难的，但测量矩阵Φ在满足条件CS1～CS3时求解式(2)和式(3)是等价的[1]，也就是说满足CS1～CS3条件的测量矩阵同样可以恢复出原信号。本文测量矩阵的设计将以CS1～CS3为准则。

普通循环矩阵是基于矩阵第一行元素依次循环得到，即第二行在第一行的基础上左移或右移一位，第三行在第二行的基础上左移或右移一位(也可看成第三行是在第一行的基础上左移或右移两位)，其余行采用相同的方法依次产生。事实上，由满足特定分布的随机数生成的随机矩阵或将某一正交矩阵的行列进行随机的互换而得到的矩阵与任一给定矩阵的不相干程度也非常大[7]。本文将在普通循环矩阵的基础上引入随机循环的思想，即矩阵的第2～M行元素将通过第一行元素的随机循环得到。在随机循环中，为了确保不产生重复的行向量，将根据生成的M-1个均匀随机数来决定第i行相对于第一行的循环步数。广义轮换矩阵[6]通过对部分矩阵元素乘以常数a(a>1)来提高列向量之间的不相干性。事实上，对Toeplitz结构的矩阵的部分元素有规律的乘以常数a(a>1) 可以增大矩阵的最小奇异值。矩阵的最小奇异值和其线性独立性是密切相关的，增大矩阵的最小奇异值，可以使其线性独立性增强；而当其最小奇异值趋于0时，其独立性也逐渐消失[11]。综上所述，本文在参照普通循环矩阵生成方法时，通过生成的均匀随机数对行列式进行随机循环以得到测量矩阵的其他行元素，同时结合广义轮换矩阵的优点构造出基于行列式随机循环的测量矩阵。

具体构造过程如下：

1)采用[-1，1] 作为向量原子：使用RANDOMIZE-IN-PLACE算法(该方法可以产生N个数的均匀随机排列[12])随机生成值为1～N的N个随机数，存在一维数组Arr中；然后将这N个随机数中小于N/2的数置为-1，大于N/2的数置为1，从而确保Arr让每个元素都满足特定概率(P(μi=+1)=P(μi=-1)=0.5)的随机数组。

2)同样以RANDOMIZE-IN-PLACE算法随机生成值为 1～(M-1) 的M-1个随机数用于第2～M行的随机循环，M-1 个随机数存在一维数组Cir(数组下标从1开始)中。这些用于矩阵循环的均匀随机数可以进一步增加测量矩阵与信号之间的非相干性，保证测量矩阵满足CS1～CS3条件。

3)将Arr=[μ1,μ2，…，μN]作为测量矩阵的第一行。通过步骤1)生成的随机数组使得矩阵行元素具有跟噪声类似的独立随机性。

4)测量矩阵第i(i=2，3,…,M)行的构造方法是：从数组Cir中选取Cir[i-1]作为第i行的相对于第一行的循环步数，例如：第二行而相对第一行向右循环Cir[1]步；同时为了进一步增大元素间的不相干性，改进参考广义轮换矩阵中的方法，在每次循环后将前Cir[i-1]个元素同时乘以常数a或b(如果i是偶数则乘以常数a，否则乘以常数b，且b>a>1)作为测量矩阵的第i行。如前所述，对每行的前Cir[i-1]个元素乘以常数a或b增大了矩阵的线性独立性。

3 实验结果与分析

本节主要对文中提及的常用测量矩阵和新测量矩阵进行仿真，对比并验证新的基于行列式随机循环矩阵在信号重构上是否具有良好性能。首先，用新矩阵在M/N=0.6时，对标准256×256的图像(图像来自于南加州大学USC-SIPI image database)进行采样压缩后用新矩阵作为测量矩阵并通过OMP算法进行重构(如图1)，说明了新矩阵的可行性。然后，分别用高斯随机矩阵、Toeplitz矩阵、循环矩阵、广义轮换矩阵以及新矩阵对大小为256×256的图像进行感知处理，并通过OMP算法[13]对压缩感知后的图像进行重构。将压缩比分别为0.1，0.2，0.3，0.4和0.5 (M/N>0.5时，各类矩阵相对误差差别较小) 的重构相对误差绘制如表1。针对压缩比M/N≤0.6 (仿真数据表明M/N=0.55时重构图像和原图像的匹配度已达到0.99)情况，将得到平均峰值信噪比(PSNR)绘制在图2中。实验在Windows7的32位操作系统，CPU主频2.1 GHz配置下运行MATLAB R2009a，所得结果是50次独立重复实验的平均值。

图1 实验对比

测量矩阵不同压缩比(M/N)下的重构相对误差0102030405高斯矩阵1762312370020780015600064Toeplitz矩阵1900812945023900017400070循环矩阵1951012218028280015000051广义循环矩阵0771200265000690003300017新矩阵0278500161000570003000016

图2 常见压缩感知测量矩阵和新矩阵在同一重构算法下的峰值信噪比(PSNR)比较

衡量各类矩阵在信号重建上的性能标准主要有峰值信噪比、信噪比、相对误差、以及运算时间等。本文以能直观反映重构图像质量的相对误差和峰值信噪比作为比较标准。由图1b可以看出，新矩阵可以理想的重建出原图像，而所需的测量值仅为原始数据长度的0.6倍。由表1可以看出新矩阵的重构相对误差在相同压缩比时始终最小。由图2可以看出Toeplitz矩阵、循环矩阵以及高斯随机矩阵的性能相当。新矩阵的重建性能较常用测量矩阵(高斯随机矩阵、Toeplitz矩阵和循环矩阵)有很大的改善，这很大程度上归功于循环移位时所乘的常数，它们增大了矩阵的行向量间的独立性。仿真结果表明，新矩阵重建信号的PSNR值要比常用矩阵高出4～18 dB，并且压缩比越小新矩阵优势越明显。新矩阵重建性能整体优于广义轮换矩阵，二者在结构上的区别在于：1)新矩阵的第2-M行是通过第一行随机循环而得；2)使用a，b两个不同的常数增大矩阵的非相干性。这种改进带来的优势随着重构矩阵所需的测量数增大而逐渐减弱，这是因为二者本质上都来源于对循环矩阵的改进。

4 小结

本文在介绍压缩感知理论的基础上，研究了该理论中的测量矩阵设计。在介绍了常用的测量矩阵及其优缺点后，对性能较好且容易实现的循环矩阵进行进一步的研究。本文在循环矩阵的基础上，借鉴广义轮换矩阵的优点，提出基于行列式随机循环的新矩阵，新矩阵在实际应用中具有和循环矩阵相同的优点[5]，而新矩阵对信号的重建性能则有很大的改善。最后，通过对二维图像的仿真，对比了文中提到的常用矩阵的性能，直观地表述了新矩阵的良好性能。

[1] DAVID L DONOHO. Compressed Sensing[J]. IEEE Trans. Information Theory，2006， 52(4)：1289-1306.

[2] EMMANUEL J CANDE S. Compressive sampling[J]. Proceedings of the International Congress of Mathematicians，2006(3)：1433-1452.

[3] MASOMEH A，AGHAGOLZADEH A，MARVASTI F. Towards optimization of toeplitz matrices for compressed sensing[C]//Proc. 2013 Iran Workshop on Communication and Information Theory (IWCIT). Tehran： IEEE Press， 2013：1-5.

[4] LI K， CRISTIAN R R， SAIKAT C， et al. Piecewise toeplitz matrices-based sensing for rank minimization[C]//Proc. the 22nd European Signal Processing Conference. Lisbon： IEEE Press，2014：1836-1840.

[5] WAHEED U B，JARVIS D H，GIL M R， et al. Toeplitz-structured compressed sensing matrices [C]//Proc. the IEEE Workshop on Statistical Signal Processing.[S.l.]：IEEE Press，2007：294-298.

[6] 李浩. 用于压缩感知的确定性测量矩阵研究[D].北京：北京交通大学，2011.

[7] EMMANUEL J C， MICHAEL B W. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine， 2008， 25(2)： 21-30.

[8] EMMANUEL J C， TERENCE T. Decoding by linear programming[J]. IEEE Trans. Information Theory， 2005， 51(3)：4023-4215.

[9] JOEL A T， STEPHEN J W. Computational methods for sparse solution of linear inverse problems[J]. Proceedings of the IEEE， 2010，

98(16)：948-958.

[10] EMMANUEL J C， TERENCE T. Near-optimal signal recovery from random projections： universal encoding strategies? [J]. IEEE Trans. Information Theory，2006，52(12)：5406-5425.

[11] 傅迎华.可压缩传感重构算法与近似QR分解[J].计算机应用，2008，28(9)：2300-2302.

[12] THOMAS H C，CHARLES E L， RONALD L R，et al. Introduction to algorithms[M].3rd ed. Massachusetts，USA： MIT Press，2009.

[13] JOEL A T， ANNA C G. Signal recovery from random measurements via orthogonal matching pursuit [J]. IEEE Trans. Information Theory， 2007， 53(12)： 4655-4666.

Research on Measurement Matrix in Compressed Sensing Based on Random Circulant

WEI Congjinga， TANG Jiashanb

(a.CollegeofTelecommunications&InformationEngineering；b.CollegeofScience，NanjingUniversityofPostsandTelecommunications，Nanjing210023，China)

Compressed sensing， depending on the fact that signals are sparsely or compressive in some fixed basis， samples and compresses the signal by linear projection. Measurement matrix plays the positive role in the theory. The common measurement matrix is researched， especially the structured matrix. As minimizing the coherence is an important way to design measurement matrix， the advantages of circulant matrix and generalized rotation matrix are learned and a new method to design a measurement matrix which based on random circulant is proposed. The simulation results suggest the new matrix has better performance in signal’s reconstruction.

compressed sensing； measurement matrix； Toeplitz matrix；random circulant

TN911.7

A

10.16280/j.videoe.2015.19.002

魏从静(1989— )，硕士生，主要研究方向为现代通信中的智能信号处理；

2015-03-17

【本文献信息】魏从静，唐加山.基于行列式随机循环的压缩感知测量矩阵研究[J].电视技术,2015，39(19).

唐加山(1968— )，教授，博士，主要研究方向为现代通信中的智能信号处理、应用统计等。

责任编辑：时 雯