复合置换通风的非稳态流动

段双平，敬成君

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621000；2.四川大学 建筑与环境学院，四川 成都610065)



复合置换通风的非稳态流动

段双平1,2，敬成君2

(1.西南科技大学 土木工程与建筑学院，四川 绵阳 621000；2.四川大学 建筑与环境学院，四川 成都610065)

以两开口单区建筑为研究对象，采用理论分析方法，推导出风机与热压共同驱动的复合置换通风的非稳态数学模型。研究了机械风量、两开口面积比和无量纲特征时间对室内热分层高度和自然通风量的影响。研究结果表明:在复合置换通风中，增大机械风量使热分层高度增大而自然通风量减小。无量纲特征时间增大，使热压主导通风模式存在所对应的机械风量的上限值减小。对于机械送风，开口面积比增大引起热分层高度和自然通风量随机械风量的变化率增加，热压主导模式存在所对应的机械风量的上限值增大，而对于机械排风，情况相反。当两开口面积相等时，采用机械送风和机械排风的效果是一样的。

复合置换通风；自然通风；热分层

0 引言

日益突出的常规能源消耗问题和环境问题使自然通风越来越受到人们的重视。但常规自然通风难以有效控制且通风效果不稳定,而利用机械通风来辅助自然通风,可以获得良好的通风效果，同时达到节能的目的。自然通风与机械通风联合使用或交替使用的技术称为复合通风技术[1]。

置换通风与传统的混合通风方式相比较，可使室内工作区获得较高的通风效率[2-3]。在以热压为主导的自然或复合置换通风建筑中，气流产生明显的热力分层现象。热分层高度、自然通风量和室内空气所受到的浮升力呈现非稳态特征。文献[4]采用实验和理论分析方法研究了热分层高度的非稳态变化。文献[5]采用数值模拟方法研究了热分层高度的非稳态变化，并得到了文献[4]的实验结果的验证。文献[6-7]研究了室内热源强度突变和周期性变化过程中的热分层界面的非稳态变化特性。文献[8]阐述了建筑围护结构的热损失、蓄热对置换通风的动态特性的影响。文献[9]着重分析了建筑几何形状、内热源强度及室外风压对自然置换通风暂态特性的影响。

前人对置换通风的研究侧重于自然置换通风或机械置换通风的非稳态研究，而对复合置换通风的非稳态特性的研究鲜有报道。因此，本文建立了热压与风机共同作用下的复合置换通风的非稳态物理数学模型，并着重分析了机械通风量、两开口面积比及无量纲特征时间(由建筑高度和开口综合面积组成的无量纲参数)对室内热分层高度、室内空气所受到的浮升力和自然通风量的影响,其研究结果可为合理设计复合置换通风系统提供指导。

1 物理数学模型

图1为一简单两开口单区建筑，其尺寸为A×B×H,体积设为V，横断面积设为S，房间下侧开口面积为Ab,上侧开口面积为At。室内有一强度为E的理想点热源。其中，图1a为机械送风辅助热压自然通风模式，房间下侧设有一机械送风口或送风机；图1b为机械排风辅助热压自然通风模式，房间上侧设有一机械排风口或排风机。

在置换通风房间中，冷空气由下部开口进入室内后，在下部空间形成温度较低的新鲜空气区，冷气流主要沿热源上升，补充热源羽流的发展，上部空间由羽流扩散形成温度较高的区域。根据空气流量守恒原理，在送风量等于羽流量的高度上形成热分层界面。假设热分层界面离地的高度为h，下层空气温度与开口处的空气温度相等，即为To,上层空气温度为Tc,Qp为热源浮力羽流在高程h断面上的容积流率。当总通风量Q不等于Qp时，热分层高度h和上层空气温度Tc会随时间变化；直到Q=Qp时，分层高度h和上层空气温度Tc达到稳定，不再随时间变化。关于影响热分层高度的因素在文献[4]中有详细阐述。本文主要讨论机械通风量、两开口面积比对室内热分层高度、室内空气所受到的浮升力和自然通风量的影响，如图1所示。

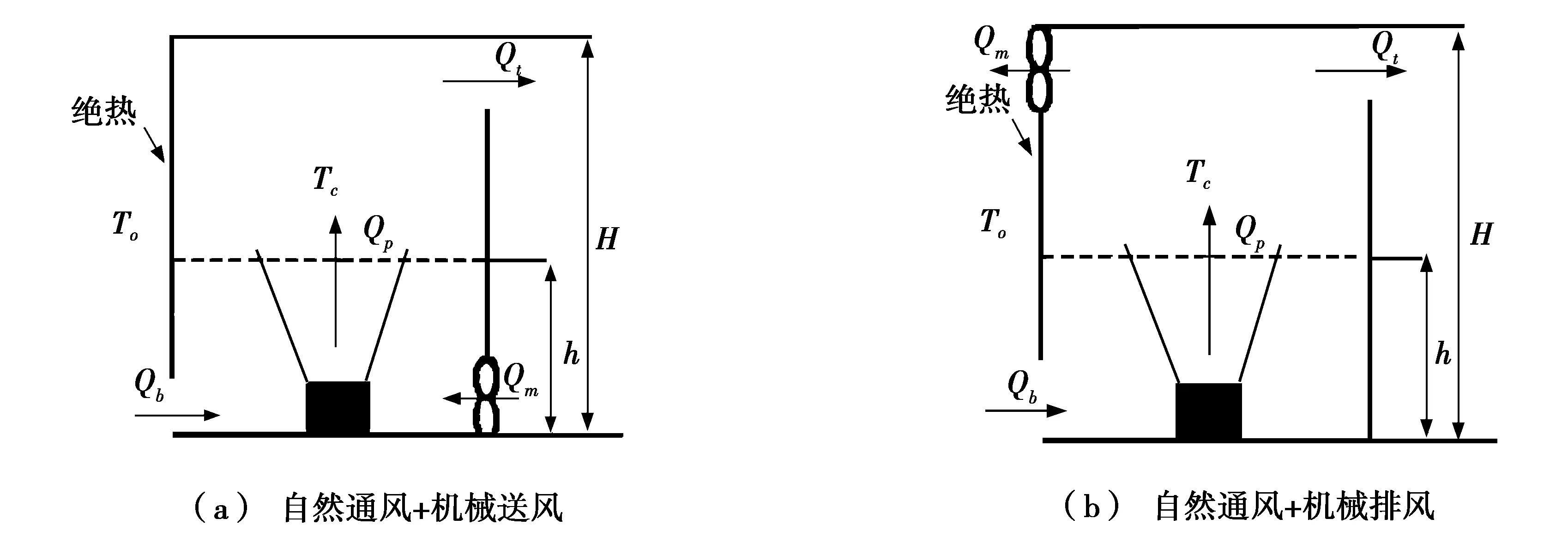
图1 建筑物理模型

在理论分析中作如下假设：

(Ⅰ)采用“二区”热分层模型。

(Ⅱ)室内空气密度采用Boussinesq假设。

(Ⅲ)建筑围护结构绝热。

(Ⅳ)不考虑辐射换热。

上层空间体积V随时间t的变化为：

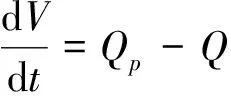
(1)

其中：Qp为热源浮力羽流在高程h断面上的容积流率；Q为总通风量，当设送风机时，Q=Qt,当设排风机时，Q=Qb。

点热源浮力羽流在高程h断面上的容积流率Qp为[10]：

Qp=cB1/3h5/3，

(2)

其中：c为常数，可取为0.143[10]；h为热分层高度，m；B为浮力通量，m4/s3。

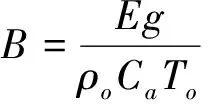
(3)

其中：E为室内热源强度，W/m2；g为重力加速度，m/s2；To为室外空气温度，℃;ρo为室外空气密度，kg/m3；Ca为空气质量热容，J/(kg·K)。

热压单独作用下的自然通风量为：

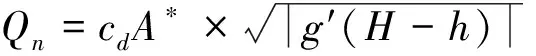
(4)

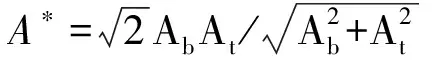
实际上,折减加速度也满足：

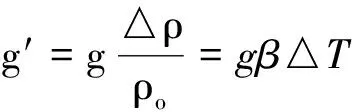
(5)

其中：△ρ为室内外空气密度差，kg/m3；β为热膨胀系数，K-1；△T为室内外空气温度差。

根据文献[11]可得热压主导复合通风模式的通风量计算模型，见式(6)～式(9)。

当风机送风时[10]，

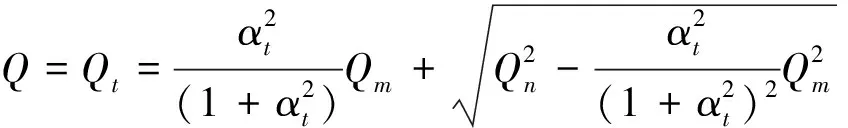
(6)

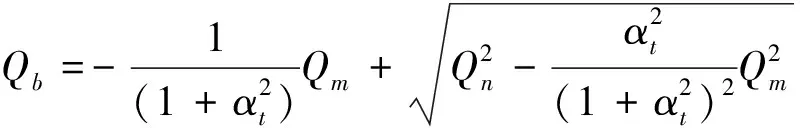
(7)

当风机排风时[10]，

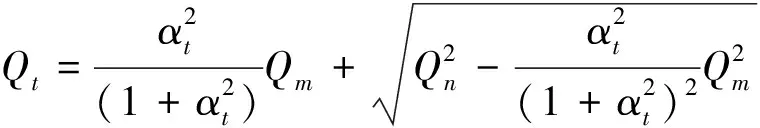
(8)

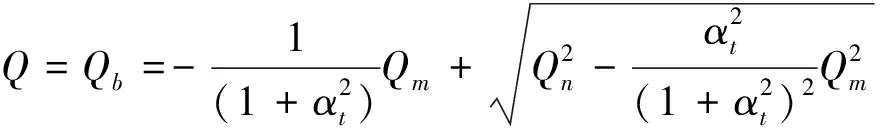
(9)

式(6)和式(7)必须满足下列条件[11]：

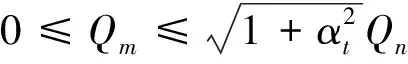
(10)

式(8)和式(9)必须满足下列条件[11]：

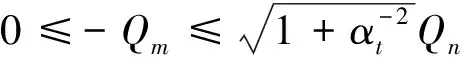
(11)

其中：Q为总通风量，m3/s；Qt为通过上侧开口的风量，m3/s；Qb为通过下侧开口的风量，m3/s；Qm为机械通风量，送风为正，排风为负，m3/s；αt为开口面积比，αt=At/Ab。

根据文献[12],式(5)右边为浮升力，故折减加速度表征了浮升力的大小，同时表征了自然置换通风上下层空气温度差大小。

上层空间体积为：

V=S(H-h)，

(12)

其中：S为房间断面面积，m2；H为房间高度，m；h为热分层界面高度，m。

当设送风机时，Qm>0,将式(2)、式(6)和式(12)代入式(1)中得：

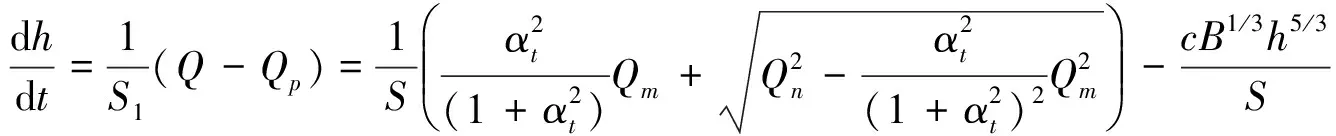
(13)

当设排风机时，Qm<0,将式(2)、式(9)和式(12)代入式(1)中得：

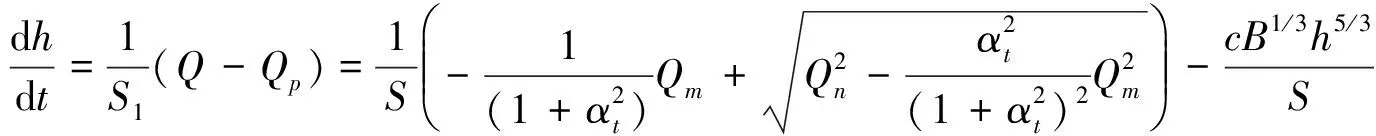
(14)

根据热平衡原理，上层空气温度Tc随时间的变化满足：

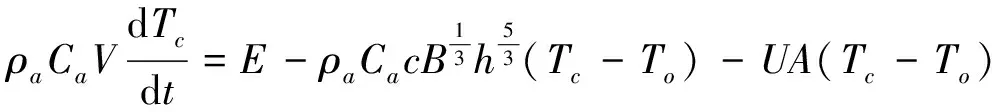
(15)

其中：Tc为上层空气温度，℃；ρa为上层空气密度，kg/m3；U为建筑围护结构的传热系数；A为建筑围护结构表面面积。

式(15)变形为折减加速度随时间的变化关系：

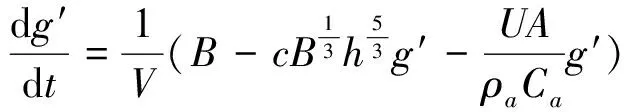
(16)

将式(13)、式(10)、式(14)、式(11)和式(16)无量纲化，分别得式(17)～式(21)。

送风时，

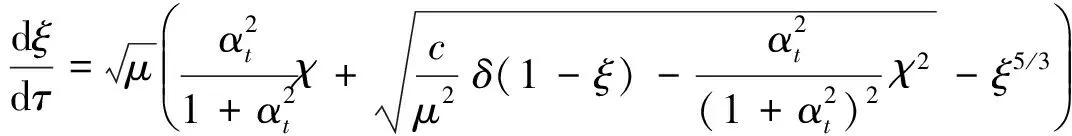
(17)

式(17)必须满足式(18)，由式(10)可得：

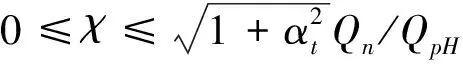
(18)

排风时，

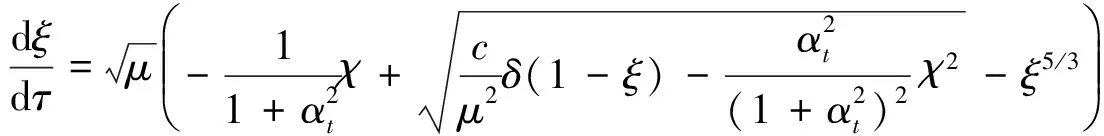
(19)

式(19)必须满足式(20)，由式(11)可得：

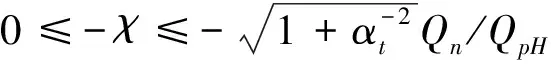
(20)

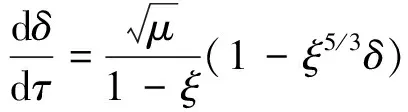
(21)

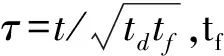
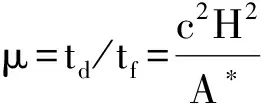
由式(4)可得无量纲自然通风量：

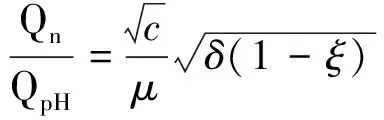
(22)

其中，QpH为点热源浮力羽流在高程H断面上(即房间天花板)上的容积流率，QpH=cB1/3H5/3。

2 结果分析与讨论

用四阶龙格库塔法求解方程(17)、方程(19)和方程(21)。初始时刻，无量纲热分层高度ξ=0，δ=1.0。所得结果绘制的曲线如图2～图4所示。

2.1 无量纲热分层高度、无量纲自然通风量随无量纲时间的变化规律

图2和图3分别为机械送风辅助热压复合通风模式和机械排风辅助热压复合通风模式的无量纲热分层高度ξ及无量纲自然通风量Qn/QpH随无量纲时间τ的变化规律。其中，μ=1.0，αt=2.0。

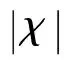
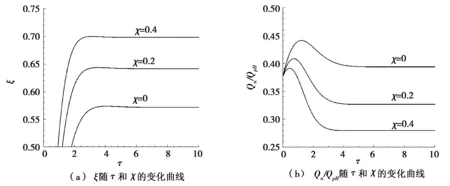
图2 机械送风时，ξ及 Qn/ QpH随τ和χ的变化(μ=1.0，αt=2.0)

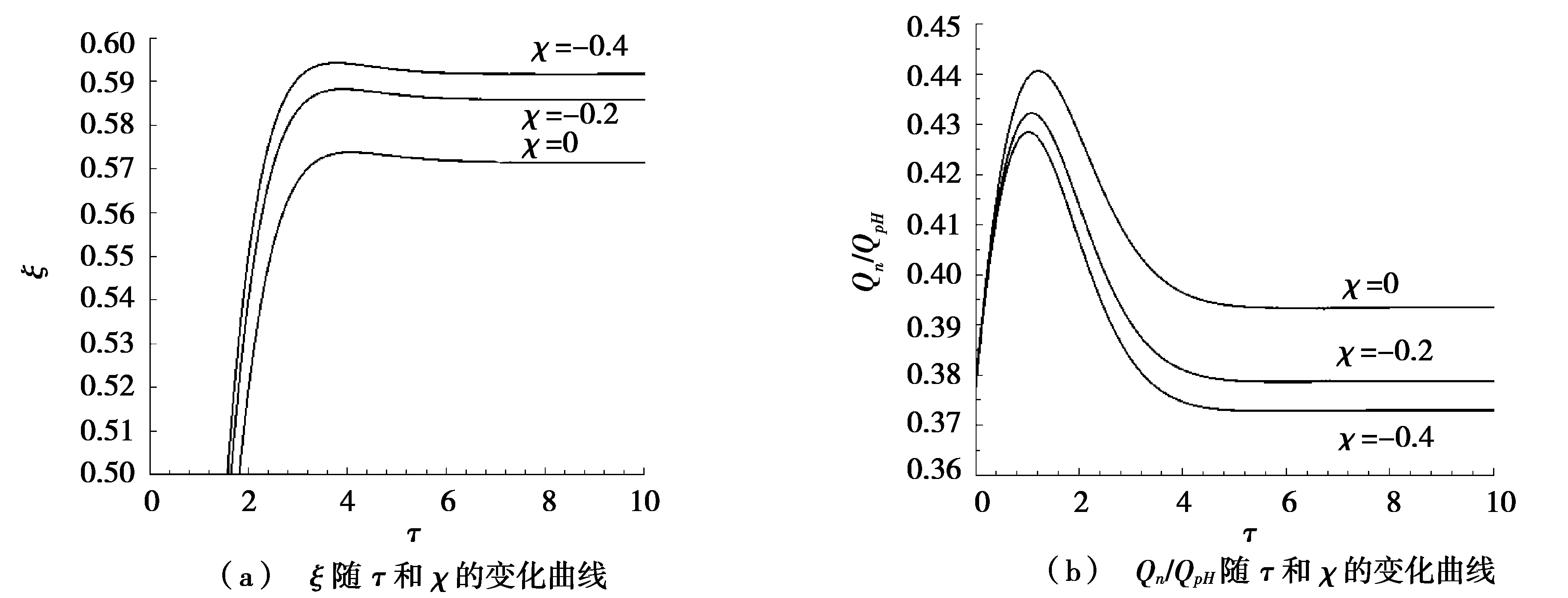
图3 机械排风时，ξ及Qn/ QpH随τ和χ的变化(μ=1.0，αt=2.0)

2.2 αt和χ对稳态下的无量纲热分层高度和无量纲自然通风量的影响

图4显示了系统达到稳态时，无量纲热分层高度ξ、无量纲自然通风量Qn/QpH及Qt/QpH(排风时)或Qb/QpH(送风时)随无量纲特征时间μ和开口面积比αt及无量纲机械通风量χ的变化规律。图4中，在μ=0.5的曲线上，有箭头标示，沿箭头方向为αt值的变化方向。μ=1.0和μ=2.0的曲线上，αt值的变化规律同μ=0.5。

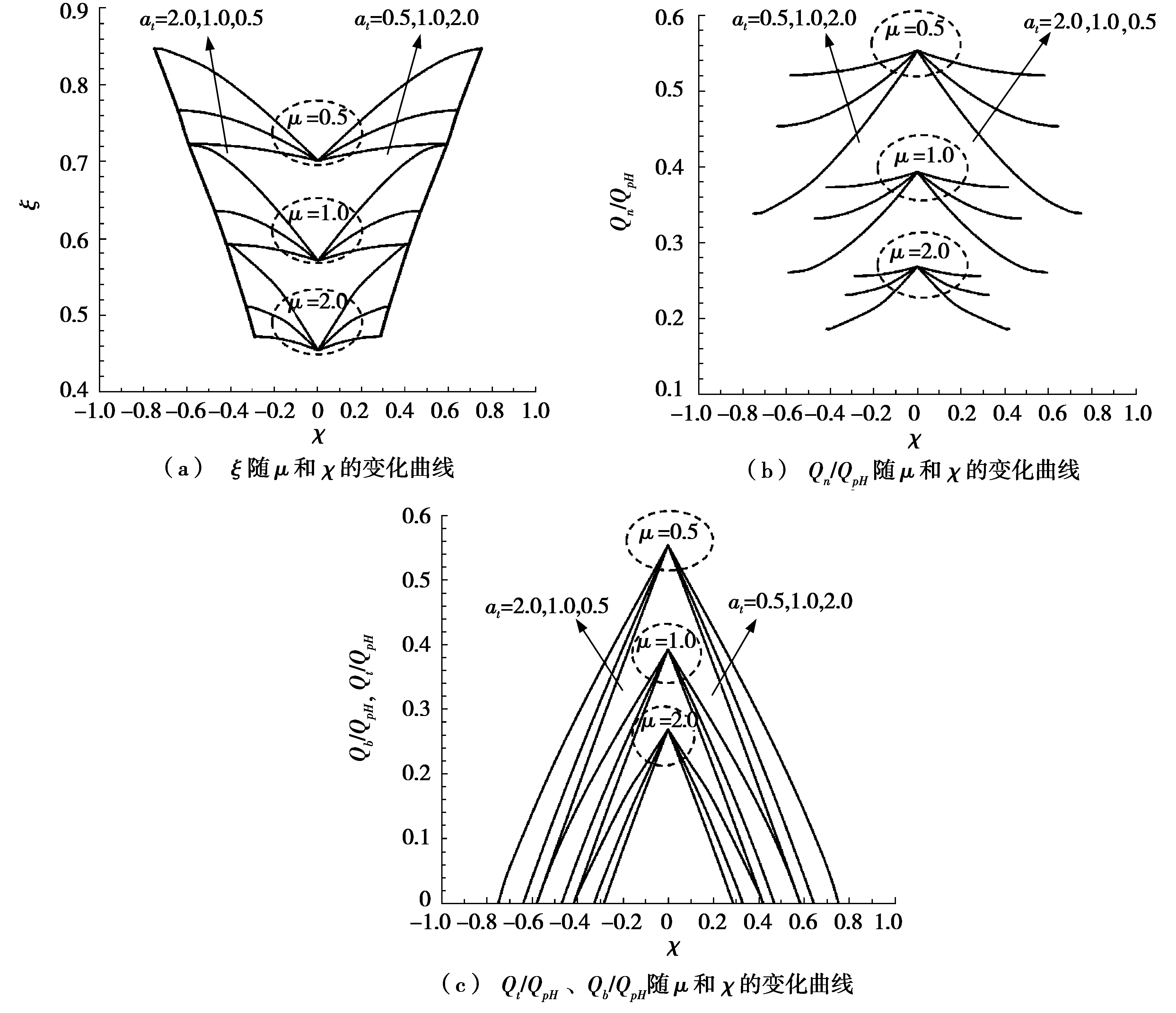
图4 ξ、Qn/ QpH及 Qt/ QpH或 Qb/ QpH随 μ和χ的变化

本文只涉及到热压主导模式的复合置换通风。很显然，图4a为3个对称图形，其中右半部分为送风时的情况，左半部分为排风时的情况。其中μ=0.5,1.0,2.0，αt=0.5,1.0,2.0。

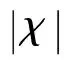
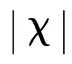
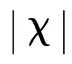
3 结论

(1)机械风量的增大使热分层高度、折减加速度及自然通风量达到稳定值所花时间减小。当αt>1时，无量纲特征时间、开口面积比相同的情况下，机械送风时的无量纲热分层高度及无量纲自然通风量随机械风量的变化幅度，比机械排风时的无量纲热分层高度及无量纲自然通风量随机械风量的变化幅度大；而当αt<1时，情况就相反。

(2)当无量纲特征时间和开口面积比一定时，热分层高度随着机械通风量的增大而增大。

(3)当开口面积比一定时，无量纲特征时间增大，热压主导模式存在所对应的无量纲机械通风量的上限值减小，热压主导通风模式区域缩小。

(4)当无量纲特征时间一定时，开口面积比增大，对于机械送风，热压主导模式对应的无量纲通风量的上限值增大，热压主导通风模式区域增大；而对于机械排风，热压主导模式对应的无量纲通风量的上限值减小，热压主导通风模式区域减小。当两开口面积相等时，采用机械送风和机械排风的效果是一样的。

[1]HeiselbergP.PrinciplesofHybridVentilation[R].Denmark:AalborgUniversity,2002:75-81.

[2] 李龙宇,李强民.置换通风的原理及应用[J].通风除尘,1996(1):27-31.

[3] 高春艳,梁坤峰,李军号,等.变压器室3种通风散热方案模拟研究[J].河南科技大学学报:自然科学版,2013,34(3):63-67.

[4]KayeNB,HuntGR.Time-dependentFlowsinanEmptyingFillingBox[J].FluidMJ，2004,520:135-156.

[5]KayeNB,JiY,CookMJ.NumericalSimulationofTransientFlowDevelopmentinaNaturallyVentilatedRoom[J].BuildingandEnvironment,2009,44:889-897.

[6]BolsterD,MaillardA,LindenP.TheResponseofNaturalDisplacementVentilationtoTime-varyingHeatSources[J].EnergyandBuildings,2008,40:2099-2110.

[7]BolsterD,CaulfieldCP.TransientsinNaturalVentilation-ATime-periodicallyVaryingSource[J].BuildingServEngResTechnol,2008,29:119-135.

[8]XavierF,NicolasLR.TimeDependentFlowsinDisplacementVentilationConsideringtheVolumeEnvelopeHeatTransfers[J].BuildingandEnvironment,2012,50:221-230.

[9]EconomidouM,HuntGR.TransientFlowsinEnclosures:AGeneralisedApproachforModellingtheEffectsofGeometry,HeatGainsandWind[J].BuildingandEnvironment,2010,45:2607-2619.

[10] Morton B R,Taylor G I,Turner J S.Turbulent Gravitational Convection from Maintained and Instantaneous Sources[J].Proc Roy Soc Lond A,1956,234:1-23.

[11] Leung H.Analysis of Natural and Hybrid Ventilation in Simple Buildings[D].Hong Kong:The Degree of Master of Philosophy at the University of Hong Kong,2003:60-83.

[12] 杨世铭,陶文铨.传热学[M].4版.北京:高等教育出版社,2006:266-267.

国家自然科学基金项目(51208442)

段双平(1974-),女,湖北浠水人,副教授,硕士,主要从事自然通风和太阳房热特性研究;敬成君(1965-),男,通信作者,四川南充人,教授,博士,主要从事工程热物理问题的研究.

2014-10-13

1672-6871(2015)04-0062-06

TU834.1

A