基于压缩感知的粒子滤波跟踪算法

吴晓雨，吴凌琳，杨 磊

（中国传媒大学信息工程学院，北京100024）

基于压缩感知的粒子滤波跟踪算法

吴晓雨，吴凌琳，杨 磊

（中国传媒大学信息工程学院，北京100024）

针对运动目标跟踪存在的目标遮挡和光照变化问题，提出一种基于压缩感知的粒子滤波跟踪算法。将改进的压缩感知跟踪算法提取的特征融合到粒子滤波跟踪框架中，并对压缩感知提取的特征和原始粒子滤波中的颜色特征进行可信度判定，能够较好地处理图像序列中由于目标遮挡和光照变化所带来的影响。此算法在公开数据库中进行测试，实验结果表明，提出的算法与已有改进压缩感知跟踪算法和粒子滤波跟踪算法相比，鲁棒性更好，能准确实时地对目标进行跟踪。

运动目标跟踪；粒子滤波；压缩感知；可信度判定

0 引 言

运动目标跟踪作为机器视觉研究领域中的一个研究热点，已经被广泛应用到智能人机交互、交通安全监控、医疗成像、军事指导、天文探测、电视制作等领域。作为一个研究热点，运动目标跟踪针对不同的环境场景存在不同的问题，如目标旋转、大小改变、光照变化、目标遮挡等，这些问题都给目标跟踪带来不同方面的难题。

近年来，针对这些问题，学者们提出了不同的跟踪算法。文献［1］提取了目标区域的SIFT特征并结合meanshift的跟踪算法，较好地解决了跟踪目标的尺度及旋转变化的问题。文献［2］提出的局部无序跟踪（locally orderless tracking，LOT）算法，对于运动目标大小变化，都能有效地跟踪。但文献［1- 2］对于光照变化和有遮挡的运动跟踪鲁棒性有待提高。文献［3- 5］基于粒子滤波框架实现对目标的跟踪，粒子重采样策略较好应对了目标被遮挡问题，但在目标环境的光照发生变化时，粒子滤波的鲁棒性很差。文献［7］基于文献［6］的压缩感知跟踪（compressive tracking，CT）算法提出了改进的算法，在原始的特征提取矩阵的基础上，生成一个提取灰度的特征提取矩阵，该算法能在目标形态和光照发生剧变等情况下准确实时地跟踪目标。但当目标被遮挡时，改进的CT算法则由于正负样本不断更新，正样本被遮挡物取代，导致遮挡后无法跟上。

视频序列中，经常会同时出现目标遮挡和光照变化的情况，而上述算法都不能对其进行有效的跟踪。针对上述存在的跟踪问题，本文首先剖析了粒子滤波跟踪和压缩感知跟踪算法的优缺点，而后提出了一种基于压缩感知的粒子滤波跟踪算法，即在粒子滤波框架下结合改进的CT算法中的压缩感知提取特征。在公开测试库上的实验结果表明，提出的跟踪算法同时解决光照变化和目标遮挡时跟踪失败的问题，在复杂场景下具有较好的跟踪效果。

1 相关算法介绍

1.1 粒子滤波跟踪算法

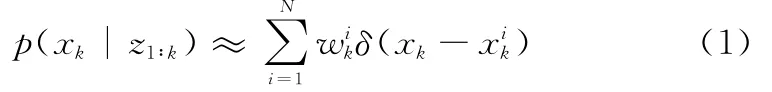
式中，δ（·）为狄克拉函数；N为粒子总数；k为序列帧数；i为粒子标志。

总体来说，粒子滤波跟踪［810］主要步骤总结如下：首先随机采样一个粒子集并提取粒子特征；其次通过特征计算粒子权重来表示后验密度函数，找到最相似粒子作为跟踪目标；最后对粒子进行重采样。

1.2 压缩感知跟踪算法

文献［6］提出了基于压缩感知的跟踪算法，利用图像的稀疏性和压缩感知［1113］算法生成了一个稀疏的随机测量矩阵，然后图像原始特征通过向此随机测量矩阵投影，去除了大量的冗余信息，并得到压缩的低维特征。对这些低维特征采用朴素贝叶斯分类学习的跟踪算法框架进行目标分类跟踪。上述压缩感知提取特征的公式为

式中，X∈Rm×1为目标候选区域转换成1维后的信号；R∈Rn×m（n≪m）为特征提取矩阵；V∈Rn×1为特征。而式（2）中不同的R会提取出不同的特征。文献［6］对R定义如下：

式中，s通过平均概率在2～4中随机选取，文献［7］指出实际特征提取为

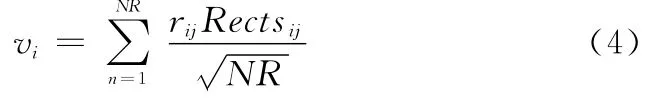
2 基于压缩感知的粒子滤波算法

由于粒子滤波跟踪算法中粒子随机采样和重采样的核心思想，使得该算法对于目标有遮挡的运动有很好的跟踪效果；但粒子滤波跟踪算法中仅用到颜色特征，对于光照的变化鲁棒性很差。而CT算法可以快速提取到低维且有效的灰度和纹理特征，有效解决粒子滤波存在的问题，然而由于对正样本的不断更新，导致在目标遮挡后正样本偏离原始目标而使跟踪丢失。因此，本文提出将CT算法中的压缩感知提取特征融合到粒子滤波框架中，能够同时解决视频跟踪过程中遮挡和光照变化的问题。本文算法流程图如图1所示，首先在目标区域周围采样两组粒子集，利用直方图和压缩感知分别提取颜色特征和灰度纹理特征；其次通过直方图距离和贝叶斯分类分别计算两组粒子的权重；再以一定的决策方法对两组粒子的跟踪结果进行可信度判定来确定当前的跟踪结果；最后进行重采样来防止粒子退化。

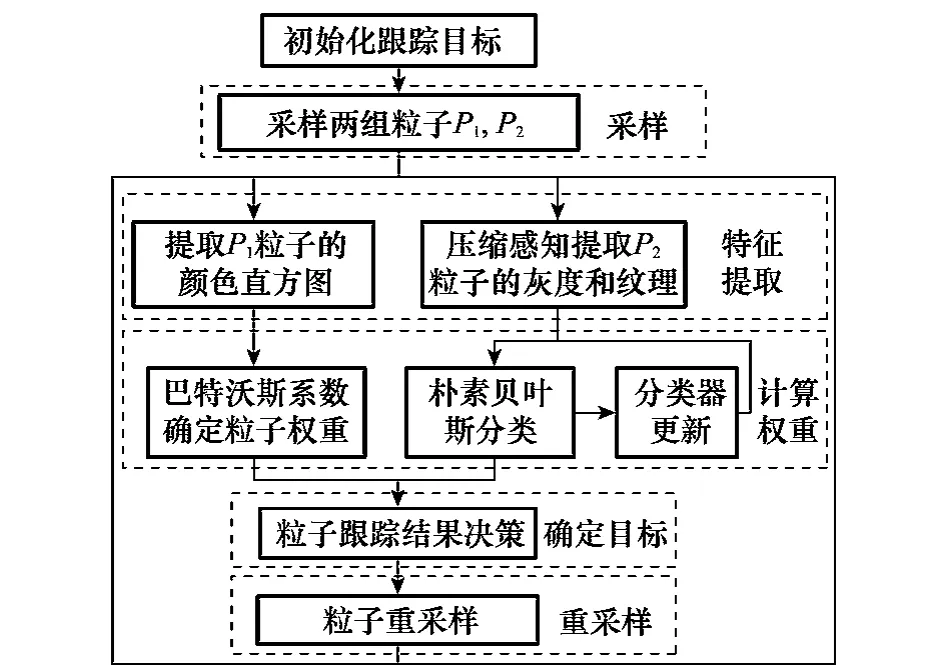
图1 本文算法流程图

2.1 粒子滤波框架下的特征提取

第一组粒子P1利用直方图来提取粒子特征，颜色直方图在目标遮挡前后变化不大，并且在目标区域周围选用了高斯分布随机采样，让采样粒子尽可能覆盖目标的各种状态。另外利用重采样降低粒子退化现象，保持粒子的有效性和多样性。因此，粒子滤波能够有效地解决目标遮挡问题。但对于跟踪过程中的光照变化，颜色直方图鲁棒性很差。

为了减少光照的影响，需要加入图像灰度和纹理等特征，而这些特征的提取比较又会大大增加算法的计算量。而压缩感知中心思想是采样和压缩共同进行，得到的压缩样本数据量远远小于传统采样所得的数据量。因此，第二组粒子P2采用压缩感知来提取图像灰度和纹理特征。

文献［7］指出特征提取矩阵（见式3）每行中1和－1同时存在的概率为0.71，提取的特征更多地表现为图像的纹理特征，纹理特征在目标形态和光照发生剧变等情况下并不稳定。为了增强跟踪的稳定性，文献［7］中利用式（3）生成R1，而后根据R1生成新的特征提取矩阵R2，从而利用R1和R2提取具有互补的纹理特征和灰度两种特征。新的特征提取矩阵生成公式如下：式中，i表示特征提取矩阵R1和R2的第i行；k表示R1中第i行中第k个非零值。因此本文参考文献［7］，将两个特征矩阵融入到粒子滤波跟踪框架中，对采样的粒子集P2提取纹理特征和灰度均值特征。

2.2 粒子权重

2.2.1 提取颜色特征的粒子权重计算

本文通过计算两组粒子的权重来表示两个后验密度函数。其中针对粒子集P1，本文采用经典的巴特沃斯距离来表示粒子与目标模板之间颜色直方图的相似度（存放的是粒子的颜色直方图），希望找到与目标颜色分布最接近的粒子。因此，巴特沃斯距离越大相似度越高，而粒子的权重也就越大。

2.2.2 提取灰度和纹理特征的粒子权重计算

针对粒子集P2，本文通过朴素贝叶斯分类器对压缩感知提取的特征进行相似性判别，寻找与标准目标最相似的粒子。对每个样本X∈Rm×1，它的低维表示是V∈Rn×1（n≪m），假定V中的各元素是独立分布的，构建朴素贝叶斯分类器为

其中，假设两个类的先验概率相等p（y＝1）＝p（y＝0），y∈｛0，1｝代表二值样本标签，y＝0表示负样本，y＝1表示正样本。文献［14］指出高维向量随机投影向量几乎满足高斯分布。所以，分类器H（V）中的条件概率p（vi｜y＝1）和p（vi｜y＝0）被假定属于高斯分布，那么

H（V）为后验概率，其值越大则与标准目标特征区域越相似，因此第二组粒子以H（V）值作为粒子权重。选取H（V）值最大的粒子作为新一帧的目标区域，并对相关系数和进行更新

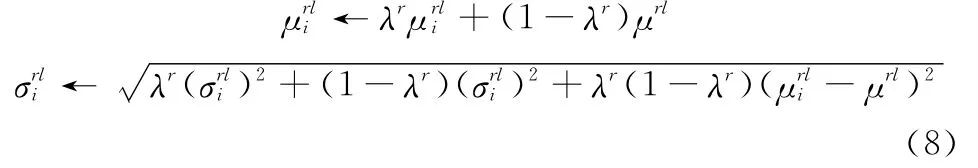
式中，l＝1代表目标样本，l＝0对应背景样本；r＝1时利用R1求取特征，r＝2时利用R2计算特征；λ对应着更新率，其值越大更新越慢，保留之前特征越多。

2.3 粒子跟踪结果决策

以两组粒子中权重最大粒子位置作为最相似粒子位置，P1和P2的最相似粒子位置分别为pk和ck，可以确定目标的最优估计位置：lk＝αpk＋（1－α）ck。这里α是融合的权重。由于两组粒子的特征都不能同时解决目标遮挡和光照变化的情况，因此需要有个判断条件来调整粒子融合权值α。

对于粒子集P1采用颜色直方图特征，粒子集越聚合，估计的目标位置方差就会越小，故基于颜色直方图特征估计的目标位置被赋予高的可信度。当在画面出现光照变化时，粒子空间位置会从原来较为集中变得相对分散，其位置方差随之变大，因此当方差大于某一阈值T1时，可判定为粒子滤波不可信（本文取T1＝45），则α＝0。

对于粒子集P2采用压缩感知提取特征，当目标被遮挡时，采样的图像片与负样本更为相似，因此H（V）将突然变小，即小于某一阈值T2（本文取T2＝2），以此来判断压缩感知提取的特征是否可信，则α＝1。

当第一组粒子空间位置方差D和第二组压缩感知概率值H（V）均在设定的阈值内，则代表两组粒子都可信。对两组粒子的结果进行归一化来确定α取值。对于P1粒子，归一化值为a＝（T1－D）／T1；对于P2粒子，归一化值为b＝（H（V）－T2）／T3，T3为设定的一个压缩感知概率中可能存在的最大值，本文取T3＝100，当b＞1时，将b置为1。那么两组粒子的融合权重为：α＝a／（a＋b）。

2.4 粒子重采样

粒子滤波器在历经几轮迭代后，大多数粒子权重都变得很小，即出现粒子退化现象，此时的粒子集将无法准确描述实际的目标后验概率分布。为解决粒子退化问题，重采样方法思想在保证粒子采样总数不变的基础下，通过复制权重较大的粒子，增多了权值大的粒子数量，消除了权值小的粒子，提高了粒子的多样性。本文对两组粒子都采用此重采样方法来防止粒子的退化。

2.5 本文算法流程

概括起来本文算法主要步骤如下：

步骤1初始化跟踪目标。手动框选初始化跟踪区域，确定跟踪目标。

步骤2采样粒子。在目标区域周围按照高斯分布采样两组粒子集P1和P2。

步骤3粒子特征提取。粒子集P1以颜色直方图提取颜色特征；粒子集P2通过压缩感知提取灰度和纹理特征。

步骤4粒子权重计算。采用巴特沃斯距离计算P1粒子与目标模板之间颜色直方图的相似度，以确定第k帧粒子集P1各个粒子的权重；以贝叶斯分类器计算P2粒子的权重，在目标位置周围进行采样正负样本，用第2.1节中提到的R1和R2，对这些样本进行压缩感知特征提取，得到特征向量V1和V2，使用式（6）对P2粒子集的特征向量V1和V2进行分类，以H（V）值大小作为P2粒子的权重。

步骤5确定跟踪目标。对粒子集P1的权重进行降序排列，找到最大权重粒子作为粒子滤波的参考位置pk，并计算粒子空间位置方差D；找到粒子集P2中最大分类值Hmax的粒子作为压缩感知的参考位置ck。

将两组粒子的参考位置pk和ck加权：lk＝αpk＋（1－α）ck。当D＞T1时，α＝0；当Hmax＜T2时，α＝1（本文T1取45，T2取2）；当D≤T1且Hmax≥T2时，将两组粒子的值分别归一化为a和b，则α＝a／（a＋b）。

步骤6对两组粒子进行重采样，粒子权重大的位置粒子数增加，权重小的位置粒子数减少。

3 实验结果与分析

3.1 算法实验结果

实验基于文献［15］中的测试库（http：∥visualtracking.net），该测试库包含目标遮挡、光照变化等多种情况的视频序列。实验在Win7系统上利用vs2010结合OpenCV2.4.5实现本文算法、粒子滤波算法［5］和改进的CT算法［7］3种算法，并在Matlab上对实验数据进行分析比较。

针对目标遮挡的情况，本文以序列David3为例进行分析。图2为3种算法对David3序列中发生目标遮挡的第81帧前后序列图像的跟踪效果。由图2可以看出，因目标遮挡，改进的CT算法因正样本更新为目标遮挡物导致跟踪错误，而粒子滤波算法因保留初始目标作为跟踪模板跟踪正确，本文提出的的自适应算法跟踪正确。因本文算法将改进的CT算法和粒子滤波结合，根据第2.3节提到的算法可信度判定准则，依据H（V）的值判定CT算法不可信，及时将其特征排除，即只利用粒子滤波算法计算的第一组粒子位置有效地在目标遮挡后恢复跟踪。

图2 3种算法对David3序列的测试效果

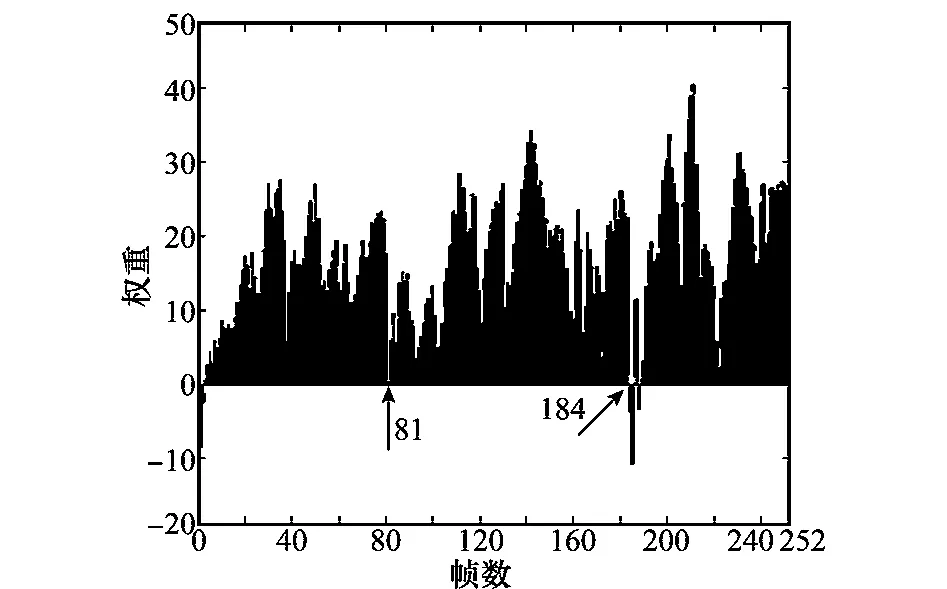
图3 每帧图像P2粒子集中最相似粒子的H（V）值

图3是本文算法中每帧P2粒子集中最相似粒子的H（V）值数据统计图，在第81帧和第184帧时，H（V）都出现急剧变小的情况。根据第2.3节的算法可信度判定准则，判定在第81帧和第184帧时压缩感知提取的特征不可信，而该序列正是在第81帧和第184帧处出现目标被遮挡，因此本文提出的依据H（V）的判定准则对于CT算法不可信时，能准确地进行判定。

针对光照变化的情况，本文选取序列Singer2来进行分析，Singer2是歌手在舞台表演的视频，其中多次出现灯光闪烁，即光照变化的情况。本文选取第11帧处的光照变化进行分析。图4是3种算法在视频序列中出现光照变化的第11帧前后序列图像的跟踪效果。

由图4可以看出，在第11帧处由于光照变化导致标准位置模板与目标模板相似度低，导致后续帧（如第33帧）基于粒子滤波跟踪失败；而改进CT算法由于正样本的不断更新，在后续帧（如第33帧）跟踪结果正确。本文算法根据第2.3节提到的算法可信度判定准则，通过计算粒子集P1粒子位置方差判定粒子P1失效，自动利用粒子集P2压缩感知的粒子位置估计准确地跟踪到了目标。

图4 3种算法对Singer2序列的测试效果

图5中可以明显看到，第11帧处，粒子位置方差有突然变大的现象，可见本文采用粒子位置方法作为粒子滤波对于光照变化不可信的判定准则是可行的。因此，本文算法能有效利用改进的CT算法对于光照变化的鲁棒性，很好地在灯光闪烁等光照变化环境下对目标进行跟踪。

图5 每帧图像粒子空间位置方差

图2和图4也说明了，本文提出的融入压缩感知特征的粒子滤波算法能同时解决目标遮挡和光照变化两个问题，较单一的粒子滤波算法和改进CT算法取得了更佳的跟踪效果。

3.2 算法性能评估

评估跟踪算法的性能，除了视觉上看到的跟踪效果，在跟踪数据上也有一定的评估方法。文献［15］中提出的对跟踪算法性能评估的方法，能够从准确率和成功率两方面对算法进行客观的评估。

为进一步评估本文提出的算法，利用文献［15］的测试评估方法及给出测试库对本文算法、改进的CT算法和粒子滤波算法进行测试。将错误阈值设置为0～50，重叠阈值设置为0～1。对于测试库中25个视频共16 970帧，3种算法的准确率和成功率曲线如图6所示。从图中可以看出，本文算法在总体上准确率和成功率都优于改进的CT算法和粒子滤波算法。在图6（a）中，当错误阈值大于8时，本文算法的准确率就一直高于另外两种算法。另外，由于本文将两种算法的跟踪结果作平均，所以在较小错误阈值范围内，准确率稍微偏低一点。但结合了两种算法的核心思想后，本文算法对于目标遮挡和光照变化都有较好的跟踪效果，因此整体上的准确率也就相应地提高了。同理，在图6（b）中，本文算法的成功率整体上高于改进的CT算法和粒子滤波算法，但当重叠阈值大于0.6时，成功率略有偏低。

图6 3种算法的性能评估图

另外，算法运算速度也是评价跟踪算法的标准之一。本文对David3（640×480），Singer2（624×352），Dudek（720 ×480），Boy（640×480）等4个不同分辨率的视频序列进行测试（测试环境CPU：Intel Core i3＠2.3GHz，RAM：4GB），计算出3种算法对每帧图像的平均运算时间，如表1所示。可以看出，加入压缩感知提取的特征后，本文算法运算速度仍然满足跟踪实时性要求。本文算法对每帧图像运算时间仅比粒子滤波算法慢2～3 ms，这是由于加入的压缩感知提取的特征数据量极少，整个算法运算速度几乎不受影响。本文还将CT算法的每帧采样图像片用粒子滤波的每帧重采样替换，运算量比CT算法降低很多，因此每帧图像的运算速度比CT算法提高了一倍。

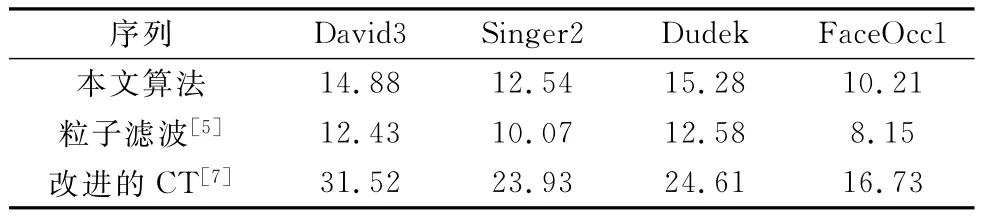
表1 算法运行速度比较 ms／fp

4 结 论

针对目标跟踪存在目标遮挡和环境光照变化的情况，本文提出将改进的CT算法中的压缩感知特征融合入粒子滤波框架中。由于利用压缩感知提取灰度和纹理特征，使得在图像信号压缩后数据量大大减少的情况下，可以有效地缓解光照变化对目标跟踪的影响。而粒子滤波中采用了颜色直方图特征，以及随机采样和重采样的核心思想，从而能在目标有遮挡的情况下，对其进行有效的跟踪。因此，融入压缩感知特征的粒子滤波算法在运算速度并没有降低的情况下，能同时解决目标遮挡和光照变化两个问题，从而提高了算法的鲁棒性。未来，如何自适应地调节判定算法可信度的阈值来使跟踪算法更为稳定是本文的研究重点。

［1］Zhao Q J，Zhang Y，Zhao D B.A scale and rotation adaptive algorithm for object tracking［J］.Journal of Central South University-Science and Technology，2013，44（6）：2354- 2360.（赵钦君，张勇，赵东标.一种尺度和旋转自适应的目标跟踪算法［J］.中南大学学报（自然科学版），2013，44（6）：2354- 2360.）

［2］Oron S，Bar-Hillel A，Levi D，et al.Locally orderless tracking［C］∥Proc.of the IEEEConference on Computer Vision and Pattern Recognition，2012：1940- 1947.

［3］Nummiaro K，Koller-Meier E，Van Gool L.An adaptive colorbased particle filter［J］.Image and Vision Computing，2003，21（1）：99- 110.

［4］Mei X，Ling H.Robust visual tracking and vehicle classification via sparse representation［J］.IEEE Trans.on Pattern Analysis and Machine Intelligence，2011，33（11）：2259- 2272.

［5］Hess R，Fern A.Discriminatively trained particle filters for complex multi-object tracking［C］∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition，2009：240- 247.

［6］Zhang K，Zhang L，Yang M H.Real-time compressive tracking［C］∥Proc.of the 12th European Conference on Computer Vision，2012：864 -877.

［7］Zhu Q P，Yan J，Zhang H，et al.Real-time tracking using multiple features based on compressive sensing［J］.Optics and Precision Engineering，2013，21（2）：437- 443.（朱秋平，颜佳，张虎，等.基于压缩感知的多特征实时跟踪［J］.光学精密工程，2013，21（2）：437- 443.）

［8］Hu S Q，Jing Z L.Overview of particle filter algorithm［J］.Control and Decision，2005，20（4）：361- 365.（胡士强，敬忠良.粒子滤波算法综述［J］.控制与决策，2005，20（4）：361- 365.）

［9］Sanjeev A M，Maskell S，Gordon N，et al.A tutorial on particle filters for online nonlinear／non-Gaussian Bayesian tracking［J］.IEEE Trans.on Signal Processing，2002，50（2）：174- 188.

［10］Djuric P M，Kotecha J H，Zhang J，et al.Particle filtering［J］.IEEE Trans.on Signal Processing Magazine，2003，20（5）：19- 38.

［11］Donoho D.Compressed sensing［J］.IEEE Trans.on Information Theory，2006，52（4）：1289- 1306.

［12］Candes E，Tao T.Near optimal signal recovery from random projections and universal encoding strategies［J］.IEEE Trans. on Information Theory，2006，52（12）：5406- 5425.

［13］Candes E，Wakin M.An introduction to compressive sampling［J］.IEEE Trans.on Signal Processing Magazine，2008，25（2）：21- 30.

［14］Diaconis P，Freedman D.Asymptotics of graphical projection pursuit［J］.The Annals of Statistics，1984，12（3）：793- 815.

［15］Wu Y，Lim J，Yang M H.Online object tracking：a benchmark［C］∥Proc.of the IEEE Conference on Computer Vision and Pattern Recognition，2013：2411- 2418.

吴凌琳（199-0- ），通信作者，女，硕士研究生，主要研究方向为图像处理、视频智能分析。

E-mail：carinel＠163.com

杨 磊（1960- ），男，教授，主要研究方向为安防领域、视频分析。

E-mail：yanglei＠cuc.edu.cn

Particle filtering tracking based on compressive sensing

WU Xiao-yu，WU Ling-lin，YANG Lei
（School of Information Engineering，Communication University of China，Beijing 100024，China）

To deal with the target occlusion problem and illumination changes in moving target tracking，a particle filtering algorithm based on compressive sensing is proposed.The extracted features are added by compressive sense of the improved compressive tracking（CT）algorithm into the framework of particle filtering tracking.The credibility of extracted features including the color features of original particle filtering and compressive sensing features is judged，which deals with the target occlusion effects and illumination changes.The algorithm is tested in public database and experimental results show that the proposed algorithm brings about better robustness and tracks targets accurately in real time in comparison with the improved CT algorithm and particle filtering algorithm.

moving target tracking；particle filter；compressive sensing；credibility judge

TN 911.73

A

10.3969／j.issn.1001-506X.2015.11.30

吴晓雨（1979- ），女，副教授，博士，主要研究方向为图像处理、视频智能分析。

E-mail：wuxiaoyu＠cuc.edu.cn

1001-506X（2015）11-2617-06

2014- 12- 29；

2015- 04- 24；网络优先出版日期：2015- 07- 06。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150706.1705.015.html

国家科技支撑计划（2014BAH10F00，2012BAH01F01- 01）资助课题