考虑轮胎侧偏特性的跨座式单轨车桥耦合振动模型
2015-06-05刘羽宇王永虎
刘羽宇,王永虎
(中国民用航空飞行学院 飞行技术学院,四川 广汉 618307)
考虑轮胎侧偏特性的跨座式单轨车桥耦合振动模型
刘羽宇,王永虎
(中国民用航空飞行学院 飞行技术学院,四川 广汉 618307)
为研究跨座式单轨交通车辆-轨道梁系统的耦合振动,以重庆市跨座式单轨交通-预应力混凝土简支梁为研究对象,建立了车辆和轨道梁的耦合振动模型。每节车辆简化为15个自由度的动力系统,并考虑所有轮胎的侧偏特性。车辆运动微分方程由拉格朗日方程导出,轨道梁简化为欧拉梁,用模态综合法建立其运动微分方程。计算了列车以不同车速通过时轨道梁的动力响应,并与实测结果和不考虑轮胎侧偏特性的模型做了比较。计算结果表明:考虑轮胎侧偏特性的模型的计算值及变化规律更接近实测值;研究竖向耦合振动问题时可不考虑轮胎的侧偏特性,研究横向耦合振动问题时应该考虑侧偏特性的影响。
桥梁工程;跨座式单轨交通;车辆-轨道梁耦合振动;侧偏特性
0 引 言
作为一种中等运量客运交通系统,跨座式单轨交通系统已在很多发达国家得到了广泛运用[1],而我国仅重庆采用。我国的跨座式单轨交通是引进日本的技术,但设计运量较日本大得多。因此,日本未出现的问题有可能会在我国出现,有必要结合我国的具体情况,对其进行深入地研究,使之成为适用于我国城市轨道交通的制式。
目前,关于跨座式单轨交通车桥耦合振动问题的研究较少,少量文献也主要见于日本[2-4]。我国对单轨交通各种问题的系统研究始于重庆单轨交通线路的修建[5],对单轨车辆与轨道梁耦合振动的研究较少,轮轨接触关系也较简单。如刘羽宇,等[6],郭文华,等[7]在简化轮胎模型时未考虑轮胎的侧偏特性;马继兵,等[8]虽然考虑了轮胎的侧偏特性,但未考虑列车行驶过程中轨道梁振动与轮胎侧偏特性的耦合因素。
笔者将在文献[6]的模型基础上,对轮胎的侧偏特性以及轨道梁振动与轮胎侧偏特性的耦合因素进行考虑,计算列车以不同车速行驶时轨道梁的动力响应,并与实测值和不考虑轮胎侧偏特性的模型比较,以验证该改进模型的可靠性,为类似工程应用提供理论依据。
1 车辆与轨道梁耦合振动模型
1.1 车辆系统
1.1.1 车辆简化模型
与普通轮轨交通车桥耦合模型中的车辆一样,跨座式单轨车辆也被简化为多个刚体,且不计车辆间的相互作用;不计转向架扭曲变形;假定各车轮始终与轨道梁接触[9-10]。将车辆离散为1个车体和2个转向架,均考虑浮沉(Z)、横摆(Y)、侧滚(θ)、摇头(ψ)、点头(φ)这5个自由度,每节车辆共15个自由度,如图1。
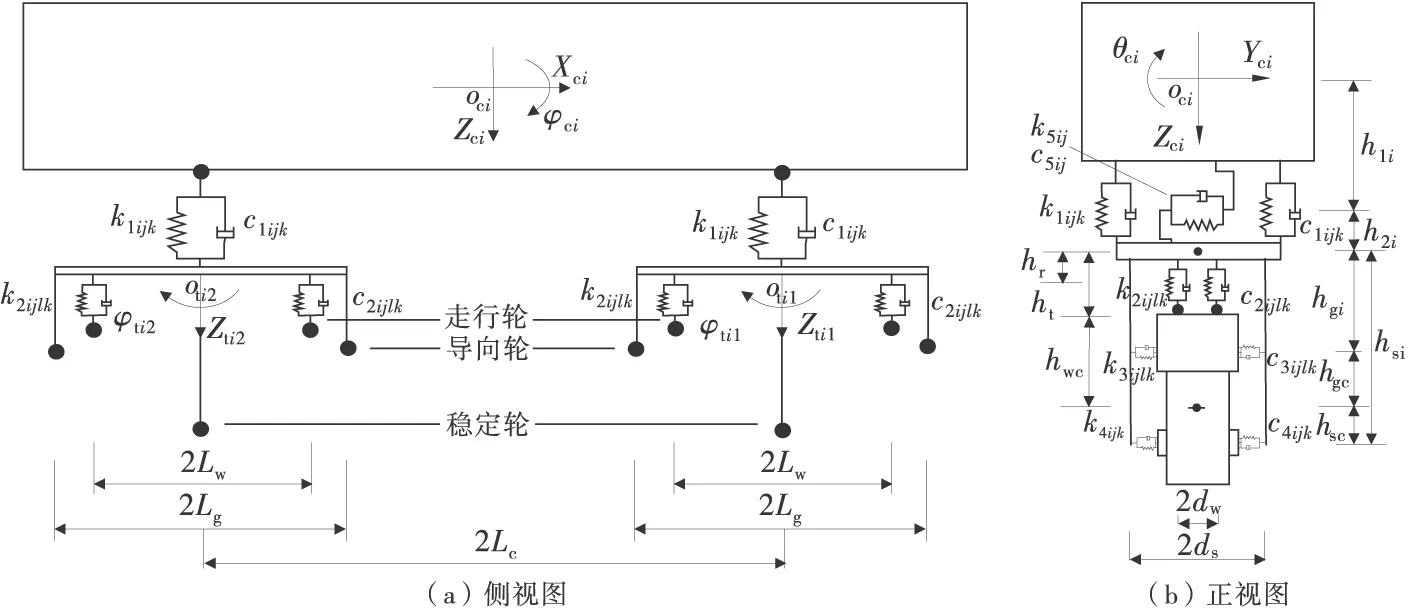
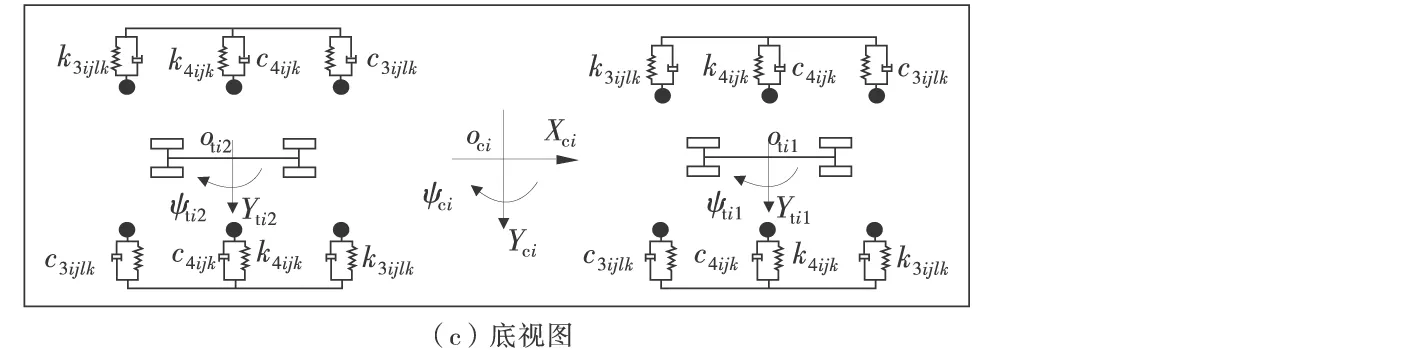
图1 跨座式车辆简化模型
图1中,Zci为车体的浮沉位移;Yci为车体的横向位移;ψci为转向架的摇头位移;θci为车体的侧滚位移;φci为车体的点头位移;Ztij为转向架的浮沉位移;Ytij为转向架的横向位移;ψtij为转向架的摇头位移;θtij为转向架的侧滚位移;φtij为转向架的点头位移;k1ijk,c1ijk分别代表空气弹簧竖向刚度、阻尼;k2ijlk,c2ijlk分别代表走行轮径向刚度、阻尼;k3ijlk,c3ijlk分别代表导向轮径向刚度、阻尼;k4ijk,c4ijk分别代表稳定轮径向刚度、阻尼;k5ij,c5ij分别代表空气弹簧横向刚度、阻尼(其中:下标i代表桥上行驶的车辆号,下标j=1和2分别代表每辆车的前后转向架,下标l=1和2分别代表每个转向架上的前后轮对,下标k=1和2分别代表车辆右侧和左侧);2dw代表走行轮横向距离;2ds代表二系悬挂横向距离;2Lc代表车辆定距;2Lg代表两导向轮轴距;2Lw代表两走行轮轴距;h1代表车体质心至空气弹簧上平面垂向距离;h2代表空气弹簧下平面至构架质心垂向距离;hg代表导向轮至构架质心垂向距离;hs代表稳定轮至构架质心垂向距离;hgc代表导向轮至梁体截面质心垂向距离;hsc代表稳定轮至梁体截面质心垂向距离;ht代表转向架至走行轮轨道面垂向距离;hr代表转向架至走行轮轮心垂向距离;hwc代表走行轮轨道面至梁体截面质心垂向距离。
1.1.2 轮胎模型
1)轮胎的径向力学特性。笔者采用的是目前应用较广的点接触式线性弹簧-黏性阻尼模型。
2)轮胎的侧偏特性。轮胎滚动时受横向力激扰会产生侧偏力和回正力矩。其大小与侧偏角(轮胎运动方向与其滚动面之间的夹角)有关,在侧偏角不超过5°时,可表示为:
Fα=kαα
(1)
(2)

当车辆速度为V时,对于走行轮可表示为:
(3)
式中:Ywijl为走行轮与轨道梁接触位置处轨道梁的横向位移。
当车辆速度为V时,对于导向轮可表示为:
(4)
式中:ag为导向轮轮心距转向架质心的横向距离;Zgijlk为导向轮与轨道梁接触位置处轨道梁的竖向位移。
当车辆速度为V时,对于稳定轮可表示为:
(5)
式中:as为稳定轮轮心距转向架质心的横向距离;Zsijlk为稳定轮与轨道梁接触位置处轨道梁的竖向位移。
3)轮胎的纵向滑转。表1列出了侧滚和摇头产生的轮胎摇头力矩。其中,r0为走行轮名义滚动半径;θwijl为走行轮与轨道梁接触位置处轨道梁的扭转角;kτ为走行轮切向刚度。

表1 转向架侧滚和摇头产生的轮胎摇头力矩
1.1.3 车辆的运动微分方程
车体运动微分方程在文献[6]中已详细列出,限于篇幅,这里仅列出转向架的运动微分方程。
转向架横摆:

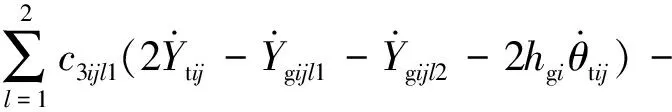
(6)
转向架沉浮:

(7)
转向架侧滚:
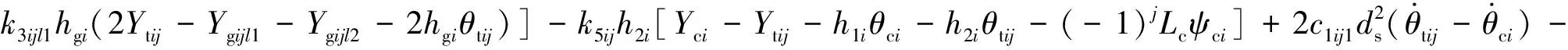
(8)
转向架摇头:
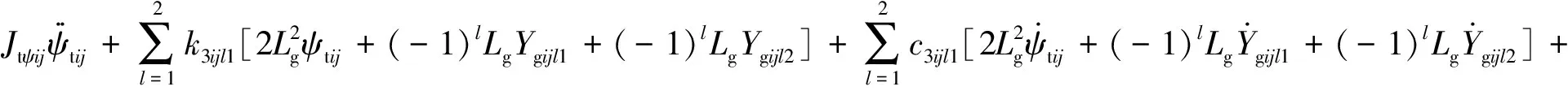
θwijl)]=0
(9)
转向架点头:
(10)

1.2 轨道梁系统
跨座式单轨交通的轨道梁一般采用I形预应力混凝土等截面简支梁,将其简化为欧拉梁,用模态综合法来计算,运动微分方程及推导过程可见参考文献[6]。轨道表面不平度采用日本的实测功率谱函数[3],并用三角级数叠加法模拟得到轨道表面不平度样本。
1.3 车辆与轨道梁的耦合振动模型
将车辆方程和轨道梁方程及轮轨关系式组合起来,即可得到车辆与轨道梁的耦合振动模型:
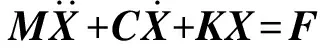
(11)
式中:M,C,K,F分别为质量、阻尼、刚度矩阵及力荷载;X为位移矢量。
2 计算结果与分析
2.1 计算参数及初始条件
由于重庆的跨座式单轨列车车辆参数与日本接近[5],故计算模型选取K.Goda[2],C.H.Lee,等[3]介绍的日本大阪车辆参数。轮胎的主要参数见表2,计算列车由两节车辆组成。选取的轨道梁计算跨径21.2 m,截面尺寸150 cm×85 cm,竖向基频6.84 Hz,横向基频3.51 Hz。计算步长0.000 1 s,轨道梁振型竖向、横向和扭转各取5阶。

表2 轮胎模型的主要参数
笔者建立的改进模型简称模型1,不考虑轮胎侧偏特性的模型简称模型2,实测数据由西南交通大学结构工程试验中心提供。
2.2 轨道梁竖向响应分析
图2为轨道梁跨中竖向动力响应随车速的变化规律,图3为车速30 km/h时轨道梁跨中竖向挠度和加速度的时程曲线。
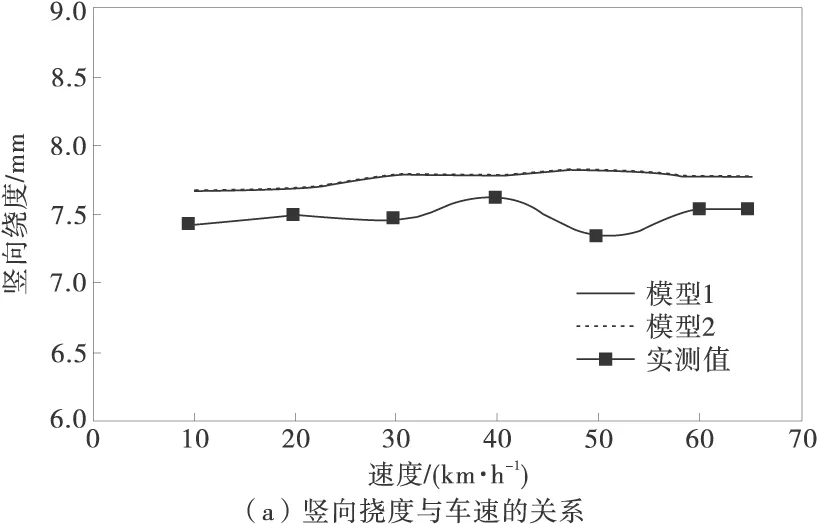
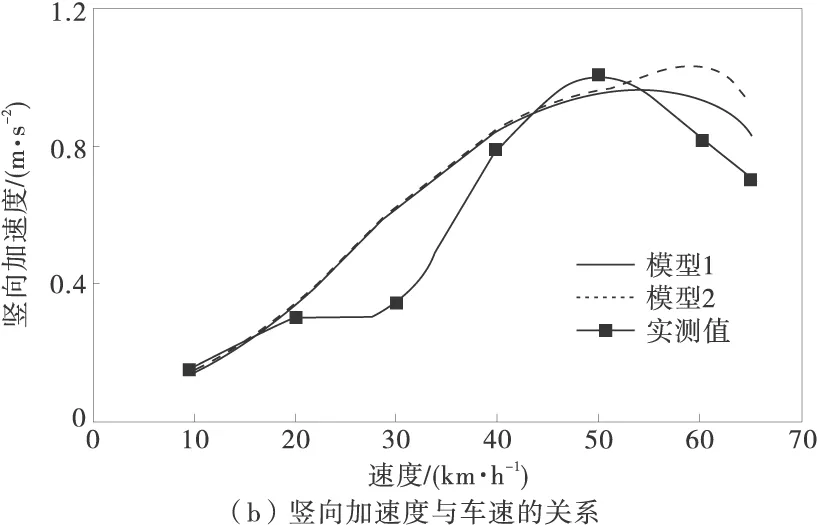
图2 跨中竖向挠度、加速度与车速的关系
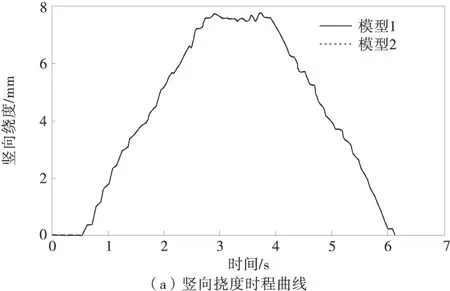
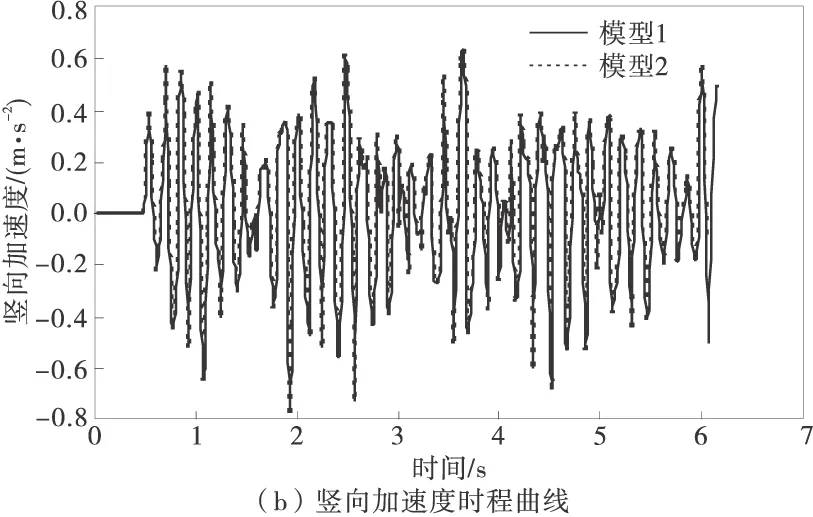
图3 跨中竖向挠度、加速度时程曲线
由图2、图3可以看出,模型1和模型2所计算的竖向挠度值和加速度值接近,时程曲线也相同,说明轮胎的侧偏特性对系统的竖向挠度和加速度影响非常小,这是导向轮和稳定轮的径向力较小的原因。因此,研究轨道梁的竖向耦合振动特性时可不考虑轮胎的侧偏特性。模型1和模型2的竖向挠度的计算值与实测值都接近,最大相对误差4.9%,竖向加速度的计算值与实测值具有相同的变化趋势,除30 km/h车速外相对误差均小于8%,说明两种模型均能较好的模拟车辆轨道梁系统的竖向耦合振动。
2.3 轨道梁横向响应分析
图4为轨道梁跨中横向挠度随车速的变化规律。由图4可见,横向挠度受车速影响较小,两种模型计算值有相似的变化规律,但模型1的挠度幅值与实测值更加接近。由此可见,考虑轮胎侧偏特性的模型1能更好的反映轨道梁的横向挠度响应。
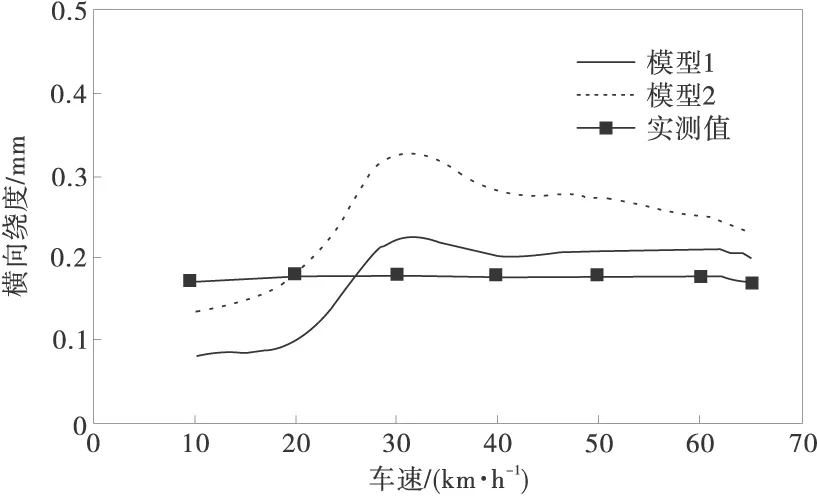
图4 跨中横向位移与车速的关系
图5为轨道梁跨中横向加速度的变化规律。由图5可以看出,横向加速度受车速的影响较大,两种模型的计算值与实测值有相同的变化趋势,均随车速增大而增加,在50 km/h时达到最大值,随后随车速的增大而减小;相比而言,模型1较模型2更加接近实测值。

图5 跨中横向加速度与车速的关系
模型1的横向位移和加速度值均小于模型2,这是因为考虑了轮胎侧偏力后增加了计算模型的阻尼的原因。因此,研究轨道梁的横向耦合动力特性时考虑轮胎的侧偏特性更符合实际情况。
图6为列车以30 km/h通过轨道梁时,轨道梁跨中的横向挠度和加速度的计算时程曲线。由于轮胎侧偏特性的原因,模型1的挠度幅值和加速度幅值比模型2明显偏小。
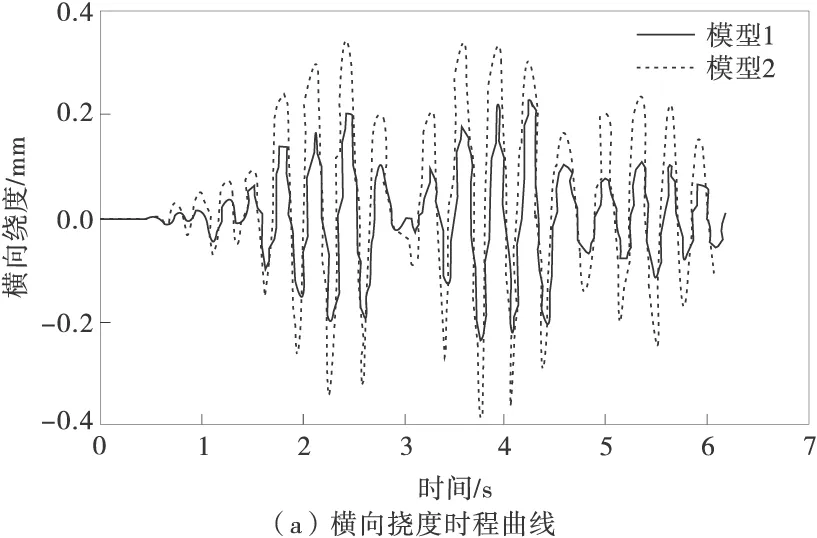

图6 横向挠度、加速度时程曲线
2.4 车辆响应分析
图7为车辆加速度随车速的变化规律。由图7可以看出,两种模型车辆的竖向和横向加速度具有相似的变化规律;模型1的车辆竖向加速度与模型2接近,但横向加速度则明显比模型2小,这也是由轮胎侧偏特性增大了系统阻尼引起的。因此,研究车辆的竖向耦合振动时,可不考虑轮胎的侧偏特性;但研究车辆的横向耦合振动时则需考虑。


图7 车辆竖向、横向加速度与车速的关系
3 结 论
1)考虑轮胎侧偏特性的模型的计算结果和变化趋势更加符合实际情况。
2)轮胎的侧偏特性对车辆-轨道梁的竖向耦合振动影响不大,但对横向振动影响较大。因此,研究车辆-轨道梁的竖向耦合振动问题时可不考虑轮胎的侧偏特性,研究横向耦合振动问题时则应该考虑。
3)轮胎侧偏特性与车辆的行驶速度和系统的振动速度有关,因此可通过增加系统的阻尼,来减小系统的振动响应。
[1] 王省茜.跨座式单轨铁路的特点及其应用前景[J].中国铁道科学,2004,25 (1) :131-135. Wang Shengqian.Characteristics of straddle type monorail railway and its application prospects[J].China Railway Science,2004,25(1):131-135.
[2] Goda K,Nishigaito T,Hiraishi M,et al.A curving simulation for a monorail car [C]// Railroad Conference.Proceedings of the 2000 ASME / IEEE Joint.Newark,New Jersey:IEEE,2000:171-177.
[3] Lee C H,Kawatani M,Kim C W,et al.Dynamic response of a monorail steel bridge under a moving train[J].Journal of Sound and Vibration,2006,294(3):562-579.
[4] Lee C H,Kim C W,Kawatani M,et al.Dynamic response analysis of monorail bridges under moving trains and riding comfort of trains[J].Engineering Structures,2005,27(14):1999-2013.
[5] 邢佶慧,宋月箫,杨庆山.跨座式单轨交通系统动力学问题研究[J].科学技术与工程,2007,7(11):2724-2726. Xing Jihui,Song Yuexiao,Yang Qingshan.Dynamic response research of straddle type monorail traffic system[J].Science Technology and Engineering,2007,7(11):2724-2726.
[6] 刘羽宇,葛玉梅,杨翊仁.跨座式单轨交通系统耦合振动特性[J].交通运输工程学报,2010,10(2):46-53. Liu Yuyu,Ge Yumei,Yang Yiren.Vibration characteristic of coupled system for straddle type monorail beam and train[J].Journal of Traffic and Transportation Engineering,2010,10(2):46-53.
[7] 郭文华,刘海涛.跨座式轻轨车与连续轨道梁空间振动分析[J].振动与冲击,2009,28(7):139-142. Guo Wenhua,Liu Haitao.Dynamic analysis of a coupled system of a monorail train of straddle type and a continuous track beam[J].Journal of Vibration and Shock,2009,28(7):139-142.
[8] 马继兵,蒲黔辉,霍学晋.跨座式单轨交通PC轨道梁车桥耦合振动分析[J].西南交通大学学报,2009,44(6):806-811. Ma Jibing,Pu Qianhui,Huo Xuejin.Vehicle-bridge coupling vibration analysis of PC rail beam of straddle-type monorail transportation[J].Journal of Southwest Jiaotong University,2009,44(6):806-811.
[9] 易晋生,顾安邦,王小松.车桥耦合振动理论在桥面不平度研究中的应用[J].重庆交通大学学报:自然科学版,2013,32(4):560-563. Yi Jinsheng,Gu Anbang,Wang Xiaosong.Application of vehicle- bridge coupling vibrations theory in the study of bridge surface roughness[J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(4):560-563.
[10] 谢秉敏,向中富,王小松,等.基于ANSYS 的车桥耦合动力分析[J].重庆交通大学学报:自然科学版,2012,31(5):935-938. Xie Bingmin,Xiang Zhongfu,Wang Xiaosong,et al.Dynamic analysis method of vehicle-bridge coupling based on ANSYS[J].Journal of Chongqing Jiaotong University:Natural Science,2012,31(5):935-938.
Vehicle-Bridge Coupled Vibration Model of Straddle Type Monorail Considering with Cornering Characteristics
Liu Yuyu, Wang Yonghu
(Flight Technology College, Civil Aviation Flight University of China, Guanghan 618307, Sichuan, China)
In order to study the interaction between vehicle and straddle type monorail beam, a simply-supported PC track beam of straddle type monorail line in Chongqing was taken as the research object to establish the coupled vibration model. Each car in the monorail train was idealized as a dynamic system of 15-degrees-of-freedom. The cornering characteristics of the tires were taken into consideration. Vehicle’s differential equations were derived by using Lagrange formulation. The track beam was idealized as Euler beam and its differential equations were derived by using modal synthesis method. The dynamic responses of the coupled system were studied at different running velocities, which were compared with the field-test data and the results of the model which has no cornering characteristics. The results show that a proper correlation is found and the model which considers cornering characteristics gives a more actual result. The cornering characteristics can be ignored when studying the vertical coupled vibration problem and should be taken into consideration when studying the lateral problem.
bridge engineering; straddle type monorail; coupled vibration system of vehicle and beam; cornering characteristic
10.3969/j.issn.1674-0696.2015.03.02
2013-10-31;
2014-05-08
国家自然科学基金-民航联合基金项目(U1333133);中国民用航空飞行学院科学研究基金项目(J2014-09);中国民用航空飞行学院青年基金项目(Q2014-007)
刘羽宇(1981—),男,四川自贡人,讲师,博士,主要从事结构振动与控制方面的研究。E-mail:mars-1@163.com。
U441.3
A
1674-0696(2015)03-007-05
