风电叶片单点疲劳加载试验振动自同步特性研究
2015-06-04张磊安王忠宾刘卫生黄雪梅
张磊安,王忠宾,刘卫生,黄雪梅
(1.山东理工大学 机械工程学院,山东 淄博 255091;2.中国矿业大学 机电工程学院,江苏 徐州 221116;3.连云港中复连众复合材料集团有限公司,江苏 连云港 222000)
振动自同步是指在一定条件下,两个同步振动系统由于存在着较强的能量和力学耦合,某些特征参数能自动趋于某个固定值的现象[1-2]。疲劳破坏是风电叶片最主要的失效方式之一,因此为了在叶片服役之前确定其抗疲劳性能,通过激励源对风电叶片进行疲劳加载试验是最有效的检测方式,试验过程中加载源与风电叶片之间构成了一个非线性能量传递系统,它们之间固存的振动自同步现象一定程度上影响着疲劳试验结果。
针对振动自同步现象,国内外若干学者均进行了研究。Abdelghani等[3]分析了系统阻尼对非理想系统稳定转速的影响,得到移动阻尼分段变化时系统振动自同步的高次谐波频率俘获区域图。Cusumano等[4-5]通过简化自同步振动非理想系统的力学模型,揭示了系统阻尼变化导致非理想系统稳态转速变化的规律,提出了增大系统阻尼可避免共振的策略。Suykens等[6-7]对单加载源系统的自同步特性进行了仿真和试验研究,再现了耦合情况下振动机械的自同步特性。国内李小号[8]对单质体非线性系统在锐共振(共振比z=0.9~1.1)情况下,双激振器作反向回转的振动自同步进行理论研究和数值仿真,运用Hamilton原理,推导出锐共振情况下非线性系统的双激振电机振动自同步运行条件。韩清凯等[9]以反向回转激励的振动系统为对象,建立了考虑电机机械特性的动力学方程,通过数值仿真计算,研究了激振器的偏心距、电机功率、偏心转子回转摩擦阻尼等参数对振动自同步的影响。张楠等[10]为了研究偏移式自同步振动机的同步特性,通过数值分析的方法,对自同步振动机从系统启动到各参数稳定运转过程进行了合理的仿真,充分验证了该类自同步振动机的同步特性。以上研究成果为本文的振动自同步特性研究提供了很好的借鉴。
本文通过构建相应的机电耦合数学模型,描述疲劳加载试验过程中的振动自同步现象,得到影响因素;然后基于相平面法构建相应的仿真模型进行数值模拟,再现了初始相位差对振动自同步现象的影响规律;最后搭建一套风电叶片单点疲劳试验加载装备,通过现场试验来检验数学模型与仿真模型的准确性,进一步揭示了单加载源与风电叶片疲劳试验过程的振动自同步特性。
1 单点疲劳加载数学模型
1.1 风电叶片单点疲劳加载方案
目前国内外风电叶片疲劳加载试验方法均以设计方提供的理论弯矩分布曲线和激振次数为依据,分别在叶片面向(xoy平面,垂直于z轴)和弦向(xoz平面,垂直于y轴),使沿叶片展向约70%处的单加载源与叶片产生共振,并按照等幅加载模式(应力比R=-1)和等效激振次数完成单点疲劳试验。疲劳试验系统的加载源为变频电动机带动偏心块回转产生的激振力,疲劳加载方案如图1所示。

图1 风电叶片疲劳加载示意图Fig.1 Wind turbine blade fatigue loading scheme
1.2 变频电动机数学模型
在二相同步旋转坐标系下,电动机的状态方程可表示为[11]
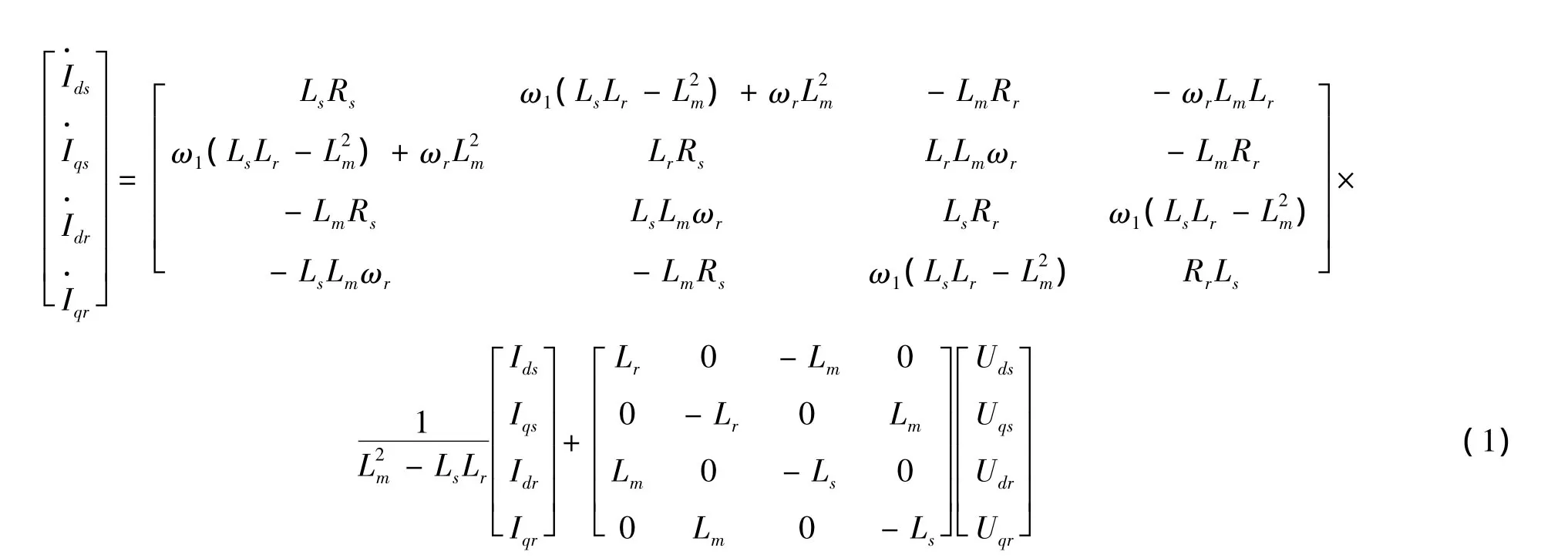

式中:Uds,Uqs,Udr,Uqr为二相同步旋转坐标系下定子端电压、转子端电压;
Ids,Iqs,Idr,Iqr为二相同步旋转坐标系下定子端电流、转子端电流;
Rs,Rr,Ls,Lr,Lm为定、转子电阻、自感和互感;
ω1、ωr为同步旋转角速度和转子角速度;
D,TL,np,Jm为阻力矩系数、电动机负载转矩、极对数和转动惯量;Id1,Id2为定子电流在d轴系上的分量;Iq1,Iq2为定子电流在q轴系上的分量。
1.3 振动系统数学模型构建
对风电叶片单点疲劳加载系统建模时做如下假设:① 叶片为弹性体,加载源及夹具等为匀质绝对刚体;② 叶片振动时,阻尼力和弹性力分别为振动速度和位移的线性函数。
在上述假设条件下,建立的风电叶片单点疲劳加载系统的动力学模型如图2所示。

图2 加载系统动力学模型Fig.2 Dynamic model of loading system
图中,oxyz为绝对坐标系;o'x'y'z'为动坐标系;φ为oxyz与动坐标系o'x'y'z'之间的夹角;o″为整个系统(叶片和加载源)的质心;om为偏心块的回转中心;M为整个系统的质量,m为偏心块质量;l=oo″,lm=oom;β为lm与x轴正方向夹角,α为l与z轴负方向夹角;ω为加载源偏心块的旋转角速度,且;r为偏心块回转半径。
针对图2,系统动能T表示为:
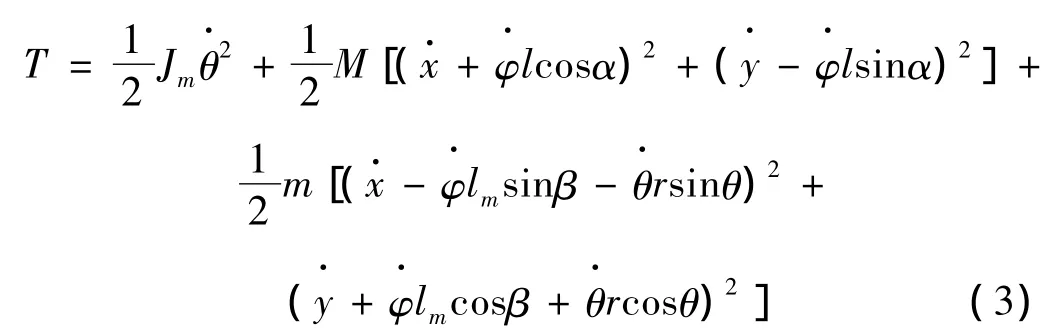
系统势能V为:
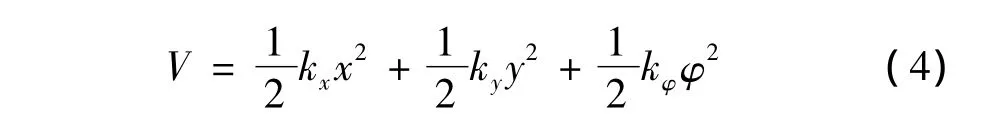
系统外力Q为:

以x、y、φ、θ为广义坐标,将系统的动能、势能代入拉格朗日方程,推导出疲劳加载系统的动力学方程:
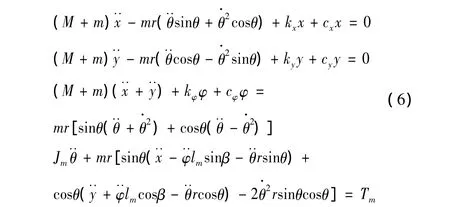
式中:kx、ky、kφ为 x、y、φ 方向上叶片刚度系数;cx、cy、cφ为x、y、φ方向上的阻尼系数;Jm为电动机的转动惯量;Tm为电动机转轴上的电磁转矩。
上式构成了风电叶片单点疲劳加载系统的机电耦合数学模型,可以得出影响振动自同步的因素很多,如初始相位差、叶片固有频率、偏心块回转半径等,它描述的是一个加载系统与振动系统相互耦合的非线性系统。
2 振动自同步仿真模型
2.1 自治系统仿真模型构建
限于篇幅,本文仅研究初始相位差对加载系统振动自同步的影响规律。为了直观地得到单加载源与风电叶片疲劳加载试验之间的振动自同步特性,拟采用相图法来表示非线性二阶系统的动态特性,将式(6)表示的数学模型简化修改成如下的自治系统。
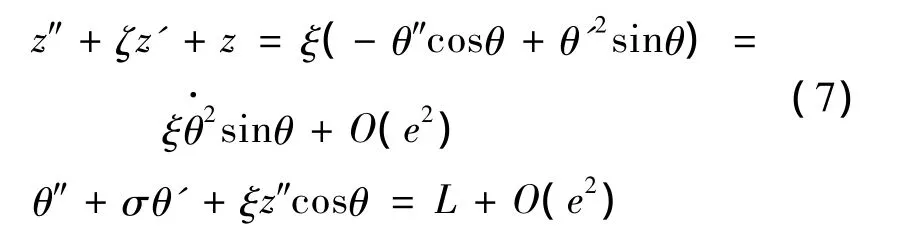
式中:

O(e2)为误差,非常小,近似为0。
2.2 振动自同步仿真特性分析
采用Matlab/Simulink软件建立仿真模型对上文构建的自治系统进行数值仿真,定量揭示风电叶片单点疲劳加载系统的振动自同步现象。针对四维相空间,定义共振超平面ω=dθ/dt=1,θ为加载源的初始相位。初始参数取:叶片初始振幅z(0)=0,叶片初始振动速度,加载源的初始相位 θ(0)=π/20,加载源回转系统初始角速度,偏心块质量m=250 kg,回转半径r=1 m,加载点刚度k=43421 N/m(通过静力试验获取),异步电动机选择Matlab软件自带的单元模块,电动机功率选择Tm=22 kW,叶片质量M=8745 kg,近似认为 β =30,cx=cy=cφ=1,仿真结果如图3所示。
从图3的运动曲线中得出,当两者的相位差为π/20时,随着加载源回转角速度的增加,叶片振幅在逐渐增大,在300 s左右时,回转角速度不再增加,而是在共振点附近上下振荡,此时回转加载系统与振动体发生“振动自同步”,振动方向的速度趋于稳定,振动位移在逐渐增大,最后趋于稳定。轴心轨迹近似是以初始轴心位置为中心的一个椭圆,轨迹大小随着角速度的增大而增大,最终趋于稳定。

图3 θ=π/20时,系统振动仿真曲线Fig.3 Wind turbine blade amplitude simulation curve,θ=π/20

图4 θ=π/8,系统振动仿真曲线Fig.4 Wind turbine blade amplitude simulation curve,θ=π/8
从图4的运动曲线中得出:在初始相位差为π/8时,随着回转角速度的递增,轴心轨迹也是近似以初始轴心位置为中心的一个椭圆。当时间到80 s时,回转角速度出现了一段水平(此时系统处于振动自同步临界点),该阶段椭圆的轨迹最大,即振动方向的振幅最大,但马上又超越了该临界点,此时,虽然回转角速度继续增大,但z方向的振幅反而变小。
从图5的运动曲线中得出:当两者初始相位差接近π时,整个过程不会产生振动自同步现象,加载源与振动体之间振动互相抵消。振动体在z方向的振动杂乱无章,整个过程的振幅较小且不稳定。

图5 θ=π,系统振动仿真曲线Fig.5 Wind turbine blade amplitude simulation curve,θ= π
3 试验研究
3.1 试验方法
将风电叶片通过若干个高强度螺栓固定在筒型加载支座上,沿叶片展向约70%处安装一个单点疲劳加载试验装备,该装备主要由三相异步电动机、变频器、齿轮减速箱、旋转偏心块和叶片夹具等组成,如图6所示。偏心质量块的臂长与重量均可调节,激光测距仪完成叶片加载点振幅的测量,12位相对式编码器完成偏心块的转速和相位测量,每个脉冲代表0.088°。监控数据通过RS485串行总线双向传输,零相位基准则通过接近开关实现,初始相位通过在夹具上安装不同夹角的木楔实现,加载试验的部分参数如表1所示。

表1 试验参数Tab.1 Test parameter

图6 疲劳加载试验Fig.6 Fatigue loading test
3.2 结果与讨论
从图7(a)中可以看出:当两者的初始相位差小于π/20时,叶片振幅从零逐渐平稳地增大,当增大到1 m左右时趋于稳定,说明两者发生了振动自同步现象,两者的步调逐渐趋于一致。根据图7(b)的试验结果,当初始相位差为π/8时,叶片振幅在经历一段先增大后减小的过程后,也逐渐趋于稳定,但是幅值比较小,仅维持在300mm左右,说明产生了较弱的振动自同步现象,这个过程中加载系统的绝大部分能量耗散在两者之间的振动自同步过程。根据图7(c)的试验结果可以得出,初始相位差为π时,叶片振幅先增大后减小,且幅值较小,整个过程中叶片振幅始终在无规律地波动,说明加载系统没有发生振动自同步现象。以上试验结论与前文的数值仿真规律基本一致。

图7 (a) θ=π/20时,风电叶片振幅变化曲线Fig.7 (a)Wind turbine blade amplitude variation curve,θ=π/20

图7 (b) θ=π/8时,风电叶片振幅变化曲线Fig.7 (b)Wind turbine blade amplitudevariation curve,θ=π/8

图7 (c)θ=π时,风电叶片振幅变化曲线Fig.7 (c)Wind turbine blade amplitudevariation curve,θ=π
4 结论
(1)风电叶片单点疲劳加载试验过程存在较强的机电耦合作用,在一定条件下机电耦合出现的结果使叶片振幅逐渐趋于稳定,即出现振动自同步现象。
(2)风电叶片单点疲劳加载系统的振动自同步特性与初始相位密切相关,数值仿真和试验均证明其一般影响规律。在加载源驱动频率与叶片固有频率相同前提下,两者的初始相位差较小时,能产生振动自同步现象,表现为叶片振幅稳定且幅值较大;随着初始相位差的逐渐增大,振动自同步现象逐渐变弱,稳定阶段时叶片的幅值也逐渐减小;当初始相位差为π时,两者不会产生振动自同步现象,表现为叶片振幅不稳定且发生絮乱。
(3)由于“加载源-风电叶片”系统之间动力响应的复杂性,使得加载系统机电耦合的影响因素很多,振动自同步过程变得比较复杂,并且机电耦合现象是固有存在的。本文的研究结果对设计解耦控制算法均具有极强的指导意义和参考价值。
[1]Anderson R G,Lorenz R.Web machine coordinated motion control via electronic line-shafting[J].IEEE Transactions on Industry Application,2001,37(1):247 -254.
[2]李小号,刘杰,刘劲涛.单质体非线性系统谐波锐共振的谐振同步分析[J].机械工程学报,2010,46(1):86 -91.LI Xiao-hao,LIU Jie,LIU Jin-tao.Analysis of harmonic oscillation synchronization for the single-mass nonlinear system under harmonic wave sharp resonance condition[J].Journal of Mechanical Engineering,2010,46(1):86 -91.
[3]Abdelghani Z D,Dane Q.Resonance capture in a damped three degree of freedom system:experimental and analytical comparison[J]. International Journal of Non-Linear Mechanics,2009,39:1128 -1142.
[4]Cusumano P,Chatterjee A.A dynamical systems approach to damage evolution tracking. part1: description and experimental application [J].Journal of Vibration and Acoustics,2012,124(2):250 -257.
[5]Boccaletti S,Bragard J,Arecchi F T.Synchronization in nonidentical extended systems[J].Physical Review Letters,2013,16(3):287-294.
[6]Suykens J A,Gestel T V,Brabanter J D.Least squares support vector machine[M].Singapore:World Scientific,2009,8(7):134 -141.
[7]Zhang T X,Wen B C,Fan J.Study on synchronization of two eccentric rotors driven by hydraulic motors in one vibrating systems[J].Shock and Vibration,2011,4(6):305 -310.
[8]李小号,刘杰,刘劲涛,等.单质体非线性系统的锐共振振动自同步研究[J].工程设计学报,2012,15(6):418-421.LI Xiao-hao,LIU Jie,LIU Jin-tao,et al.Research on vibration synchronization of single-mass nonlinear system under sharp resonance condition[J].Journal of Engineering Design,2012,15(6):418 -421.
[9]韩清凯,杨晓光,秦朝烨,等.激振器参数对振动自同步振动系统的影响[J].东北大学学报:自然科学版,2013,28(7):1009-1013.HAN Qing-kai,YANG Xiao-guang,QIN Zhao-ye,et al.Effects of exciter parameters on self-synchronous vibration system[J].Journal of Northeastern University:Natural Science,2013,28(7):1009 -1013.
[10]张楠,候晓林,闻邦椿.偏移式自同步振动机的同步特性[J].东北大学学报:自然科学版,2009,30(9):1302-1309.ZHANG Nan, HOU Xiao-lin, WEN Bang-chun.Characteristics of synchronization for self-synchronous vibration machine with center of mass deviated vibrator[J].Journal of Northeastern University:Natural Science,2009,30(9):1302-1309.
[11]来鑫,乌建中,王伟达,等.多锤联动系统的振动耦合理论及试验研究[J].机械工程学报,2012,48(3):108 -114.LAI Xin,WU Jian-zhong,WANG Wei-da,et al.Theoretical and experimental study on electromechanical coupling of joint pile-hammer system[J].Journal of Mechanical Engineering,2012,48(3):108-114.
