2DPCA 在人脸识别算法中的应用研究

李扬　周冬梅

摘要：人脸识别是借助于摄像手段采集与跟踪人脸的图像或视频流，将人脸的形状、属性等特征反映给计算机的技术。该文在人脸特征识别PCA算法基础上进一步完善的2DPCA算法，通过二者模拟实验的对照，发现后者不仅是对前者的升华补充，而且可以大幅度降低识别时间，提高识别速率。

关键词：人脸识别；PCA；2DPCA

中图分类号：TP18 文献标识码：A 文章编号：1009-3044（2015）09-0193-02

计算机视觉技术的全面发展，使得人们愈来愈将目光投入到便捷独特的智能處理中，其中包含智能监控、安全交易、交互设计等，而人脸识别技术是其中很重要的一个方面。它不但可以验证和静态使用面部特征匹配的身份，被动识别，而且易于被用户接受，友好和方便，所以成为现在人工智能领域的一个研究热点。

1 人脸识别概述

人脸识别是模式识别的一个重要组成部分，它是通过计算机为平台，处理以及规划人脸图像的分类分析，并获得有效的识别信息来描述面部特征和实现有效的识别，是一种应用于身份识别的新兴计算机技术。它主要囊括了如下几个部分：人脸图片的采集、检测、预处理、特征提取、匹配与识别[1]。

1.1 图像的采集

不同的人脸图像，如静态图像和动态图像，不同位置和不同的表情，通过相机拍摄的结果往往也不同。当用户在采集设备的拍摄范围内时，采集设备会自动搜索并拍摄用户的人脸图像。通过数学矩阵转换成计算机能自动辨别的信息，交给计算机有效的数学处理后，最终达到对人脸图像进行识别的效果。

1.2 图像的检测

人脸图像中有非常丰富的模式化特性，比如结构特性和Haar特性等。检测的目的就是寻找出其中有用的信息，主流的检测方式叫做Adaboost算法，该算法将筛选出的面部矩形特征按照加权的方式逐层升级，起着“提升树”的作用，即把一系列的弱检测算法提升成为强检测算法，进而增强检测的准确度。

1.3 图像的预处理

对于人脸的图像预处理是基于人脸检测结果，对图像进行处理并最终服务于特征提取的过程。拍摄的原始图片一般不可以直接模式转换，需要灰度校正、噪声过滤等预处理后才能清晰直观的使用。预处理的方法有很多，例如光线补偿、直方图的均衡化、归一化等。

1.4 图像的特征提取

视觉特征、像素统计特征等是很常见的特征提取方法。人脸特征提取就是针对人脸的某些特征进行的。人脸特征提取，也称为人脸表示，它是一种人脸特征建模过程。主要有两种特征提取方法：一是基于知识的表征方法；二是基于统计特性的代数方法。

1.5 图像的匹配与识别

经过预处理的特征图片发送至计算机，与计算机硬盘中的数据库进行搜索匹配，然后软件设定一个阈值，当采集的图片与原始图片的相似度接近于阀值时，将识别结果输出。图像识别是根据人脸特征模板的相似度比较来确定验证和识别人脸身份信息的过程。

2 PCA概述

在一般情况下，人脸图像的数据量非常大，庞大的计算相当繁琐，所以必需对初次采集得到的数据作适当的处理，降低计算难度，得到反映分类本质等特征。

基于以上的考虑，采用Eigenface方法（即特征脸）来进行测试，该算法可以有效地减少数据量，降低计算的难度，进而提高效率和速度。特征脸方法是人脸识别算法的经典算法，即主成分分析的核心（主成分分析的降维算法，PCA）。

PCA基本原理是数据降维，借助于特征向量矩阵，把获取的图像从高维的向量空间投影到低维，即是用维数较低的空间去重构对应的维数高的向量空间，并且还不会丢失任何图像信息。这种方法既能达到模式样本的维数压缩的效果，也能达到消除模式样本之间的相关性的作用。

3 2DPCA概述

在一般情况下，人脸图像的维数较大，而对人脸图像处理维度的PCA算法的使用局限造成计算复杂度的增加，费时又费力，故而便引进了处理图片的2DPCA二维主成分分析方法）。2DPCA方法是直接计算人脸图像，不同于PCA需要首先先将原始图像的矩阵转化为一维列向量那样，2DPCA保留了更多的结构信息，计算协方差矩阵更为准确，在图像特征提取上更加简单和直观。以下是2PDCA图像重构的原理：

设X表示n维单位列向量。可以设该图像A（m行n列）是通过线性变换的随机矩阵[2]：

[Y=AX] （1）

因此，得到图像[A]的投影特征向量Y。再令

[Yk=AXk，k=1，2，…，d] （2）

设[X1，X2，…，Xd]为最图片优投影向量，可以计算出一系列特征向量组[Y1，Y2，…，Yd]，叫做图片A的主成分向量。则[B=[Y1，Y2，…，Yd]]构成A的特征图像。

假设[X1，X2，...，Xd]在协方差矩阵最大特征值（前d个）的图像产生的特征向量经由投影后得到相应的主成分向量为[Yk=AXk，k=1，2，...，d]。令[V=Y1，Y2，...，Yd]，[U=X1，X2，...，Xd]，如果[V=AU]，那么A重构后得到：

[A=VUT=k=1dYkXTk] （3）

令 [Ak=YkXTk（k=1，2，...，d）]，这是一个和A相同大小的图片。所以，图片A的重建取决于前d个子图像，当主分量向量的个数d等于矩阵特征向量的总数时，[A=A]，样本图片重构无损；如果[d4 PCA与2DPCA的实验对比

调用ORL人脸库中[3]的头像作为原始数据，该人脸库共有[112×92]大小的照片400幅，分别来自40个人，这些照片具有不同的表情。然后使用每个人的前五张图片作为实验，筛选10个拥有最大特征值的特征向量作为投影轴投影轴上的图像，可以获得10个主成分向量，确定一个向量重构图。为清晰起见，其中的一些子图像在图2中进行了反射。此外，在图2中对特征值的递减进行了大小绘制。

在图1中观察到，第一张子图包含了大部分的原始图像的能量。k值的增加，包含的信息（能量）逐渐减小。图2显示了特征值的快速收敛至零，与图1有相同的结果。因此，用向量表示这些能量的分布来实现图片识别是合理的。所以，通过增加特征值获得的人脸图像的图像重建，作为子图像的数目愈增加，重建图像愈清晰。

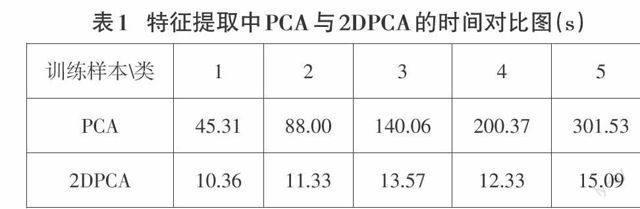
另外，PCA和2DPCA在特征向量维度相同的情形下，识别精度方面，2DPCA性能优于PCA。二者的计算速度与效率方面，表1可以看出，采用2DPCA特征提取所消耗的时间比PCA要少很多。综上所述，2DPCA比PCA有两个明显的优势：第一，它更容易准确地评估协方差矩阵；第二，在确立特征向量时，2DPCA有显著的优越性。

5 结束语

基于2DPCA的人脸特征提取方法是在研究了经典的PCA算法的基础上提出并加以改进的，通过二者的对比，2DPCA在效率和计算量方面都优于PCA，同时，人脸识别作为一种复杂的生物技术，为了达到更好的识别效果，需要在理论成熟的同时也要综合各方面科技的优势，相信在国内外学者的不懈努力下，人脸识别技术必将得到更加长足的发展！

参考文献：

[1] 肖冰，王映辉.人脸识别研究综述[J].计算机应用研究，2005（8）：1-5.

[2] LIU Ke，CHENG Yongqing，YANG Jingyu，et al.Algebraic feature extraction for image recognition based on an optimal discriminant criterion[J]. Pattern Recognition， 1993，26（6）：903-911.

[3] AT&T Laboratories Cambridge.The ORL Database of Faces.