正断层错动致地铁变形计算模型

黄 芸， 蔡奇鹏， 郭子雄， 郭力群， 苏世灼， 陈星欣

(1. 华侨大学土木工程学院， 福建 厦门 361021； 2. 华侨大学建筑设计院， 福建 泉州 362021)

正断层错动致地铁变形计算模型

黄 芸1， 蔡奇鹏1， 郭子雄1， 郭力群1， 苏世灼2， 陈星欣1

(1. 华侨大学土木工程学院， 福建 厦门 361021； 2. 华侨大学建筑设计院， 福建 泉州 362021)

针对正断层错动引起的地铁隧道变形破坏仍缺乏有效的理论预测模型的情况， 基于不排水条件下上覆土体的变形机理， 建立地铁隧道变形的计算方法. 理论模型表明， 影响隧道衬砌纵向线应变的参数有隧道半径、 土层厚度、 基岩断层错动量、 断层倾角、 隧道埋置深度和形状参数. 正断层错动影响下， 隧道拱顶衬砌分别在基岩下盘和基岩上盘一侧出现受拉区和受压区. 而隧道拱底衬砌则分别在基岩下盘和基岩上盘一侧出现受压区和受拉区. 随着隧道埋深的增加， 需要进行拉裂破坏加固的范围逐渐缩小， 并向基岩断层附近趋于集中. 而随着基岩断层倾角的增加， 隧道拉裂破坏加固区域则往基岩上盘一侧偏移， 但加固区域的大小范围受断层倾角的影响并不显著.

正断层错动； 地铁； 隧道； 计算模型

0 引言

基岩断层错动引起的地层永久变形， 对地面建筑物及地下结构物均造成严重破坏. 尤其是长距离线性构筑物， 如隧道和地下管线等[1-3]. 汶川地震造成了16条国省干线公路的隧道、 桥梁等建筑物大范围损坏， 其中穿越断层破碎带的隧道受损严重， 甚至出现衬砌垮塌. 位于希腊Rion-Antirrion峡谷的潜在正断层带， 对跨越其上的隧道修筑提出了巨大挑战[4]. 对于地铁建设选线， 同样很多情况下不可避免需要穿越潜在断层带. 不同类型断层错动引起的地层变形特征不同， 需要针对具体断层形式， 深入研究基岩断层错动引起上覆土体中地铁隧道结构的变形破坏.

熊炜等[5]采用有限元方法研究正断层环境下公路山岭隧道衬砌的受力变形特征， 并分析断层错动量、 断层倾角、 隧道埋深以及隧道与断层的交角4个因素的影响. 刘学增等[6]通过模型试验研究正交穿越75°倾角逆断层的公路隧道的破坏规律. 黄强兵等[7]通过大型物理模型试验和有限元数值模拟研究穿越地裂缝带的隧道受地裂缝活动的影响宽度以及受力特征， 得出地铁隧道斜交穿越地裂缝带的纵向设防长度. 这些针对公路隧道的研究为认识其它地下结构物的断错效应奠定了基础.

目前， 针对正断层活动引起上覆土体中地铁隧道变形破坏的研究相对不足， 相关的理论计算模型更是缺乏. 针对该问题建立一个隧道变形计算模型， 并通过独立的物理模型试验数据对计算模型进行验证， 进而展开关键因素的参数分析.

1 土体变形预测公式推导

1.1 土体变形机理的简化

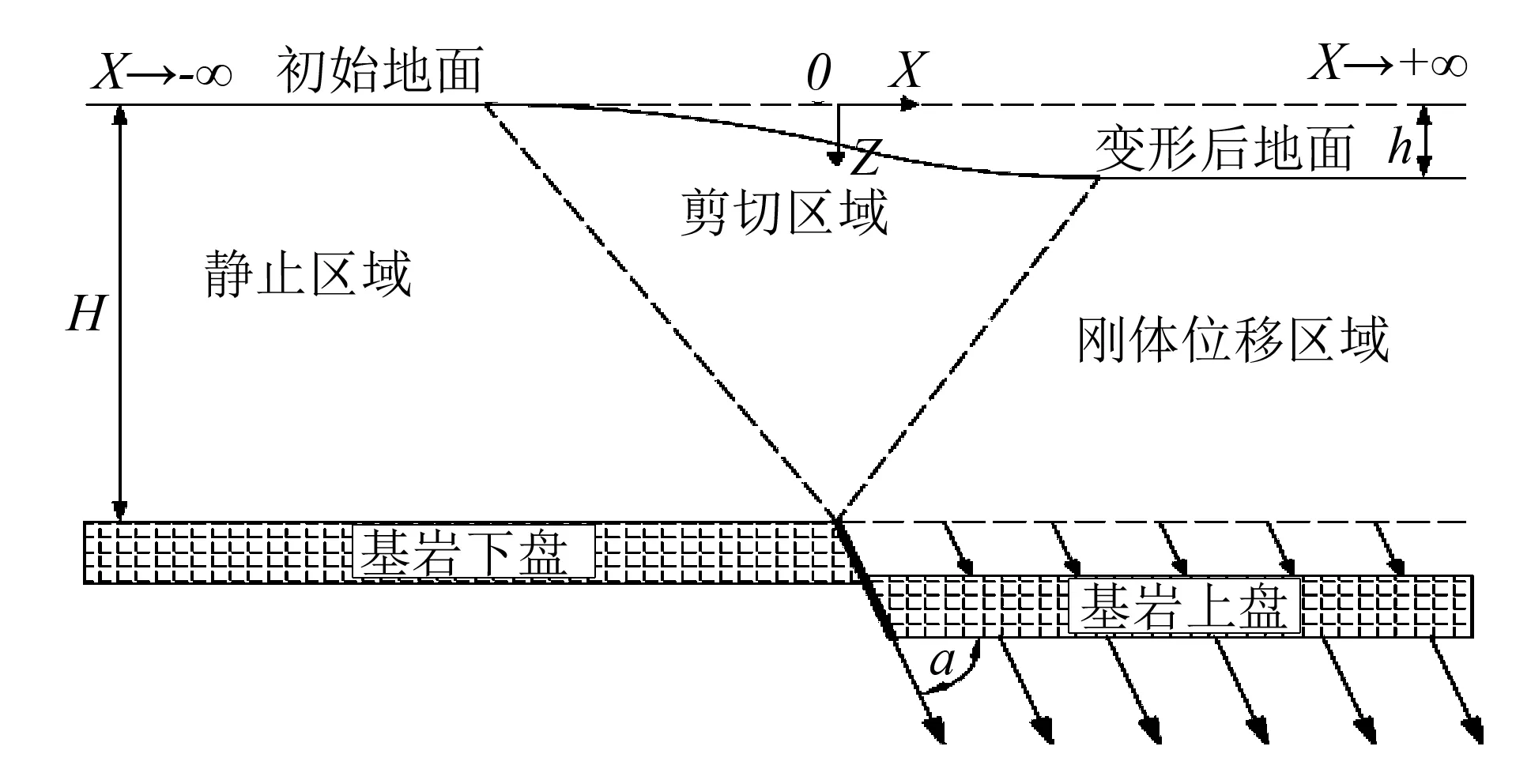
图1 正断层引起上覆土体变形机理Fig.1 Deformation mechanism of overlying soil induced by normal faulting

Cai等[8]基于离心机试验研究发现， 基岩正断层错动引起的上覆粘土变形可以简化为一个剪切变形机理. 如图1所示， 厚度为H的上覆土层受倾角为α， 错动量为h的正断层错动影响时， 土层变形区域可划分为静止区域、 剪切区域和刚体位移区域， 并可假定粘土的变形是连续的. 其中， 刚体位移区位于基岩断层上盘一侧， 区内土层厚度同样为H. 该区域内土体在基岩错动中沿着断层倾角方向移动， 移动幅值与基岩错动量近似相等. Faccioli等[9]在对1999年土耳其的Kocaeli地震震后现场调查表明， 地表断裂带集中在一有限范围内. 而紧邻地表断裂带附近， 位于断层下盘一侧的建筑物则随着基岩的正断层错动做整体斜向下位移， 建筑物结构保存完好. 这一现象与本文假定的刚体位移区的特征一致， 表明位于该区域的建筑物不会因为临近地表的永久变形而发生结构破坏.

若取基岩断层在地表的投影位置为坐标原点并建立相应坐标(见图1)， 土层变形的一般表达式可记为：dZ=dZ(X,Z,h,H,α,S)和dX=dX(X,Z,h,H,α,S). 其中：dZ是土层竖直沉降位移；dX是土层水平位移；X是土体离开基岩断层的水平距离；Z是土体与地表的竖向距离；S表示影响土体变形的相关特性.

为满足上述剪切变形机理， 土层变形的一般表达式需符合下列条件：

1) 对于位于静止区域的土体， 在断层错动的过程中保持静止(当X→-∞时，dX=0，dZ=0);

2) 对于位于刚体位移区域的土体， 在断层错动的过程中始终与基岩断层保持相同的错动方向和错动量(当X→+∞时，dX=hcotα，dZ=h).

1.2 表征土体沉降的误差方程

Roboski[10]发现， 补余误差方程可以拟合从基坑开挖角落最小土体位移到基坑开挖中心最大土体位移这一特征. 进而通过现场数据验证了选用这一拟合方程的可行性.

正断层错动引起的地表变形曲线与误差方程也有着相似的曲线特征， 可选用误差方程来拟合正断层错动引起的上覆土体变形[8, 11]. 误差方程的一般表达式为：

其中：A，B，C，D为4个控制误差方程曲线形状及位置的参数.

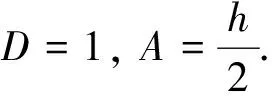
因此， 地表土体竖向位移表达式为：

此处，BZ为不随土体深度变化而变化的形状参数. 由此， 深层土体沉降曲线可表征为：

1.3 表征土体水平位移的方程

由于基岩错动的时间相对较短， 上覆粘土的变形可视为不排水变形. 因此， 可以合理地假定上覆土体变形时满足不排水条件. 上覆土体变形应满足以下方程：

将式子(4)代入(5)进行积分， 再代入①和②两个边界条件： ①当X→-∞时，dX=0; ②当X→+∞时，dX=hcotα， 可得：

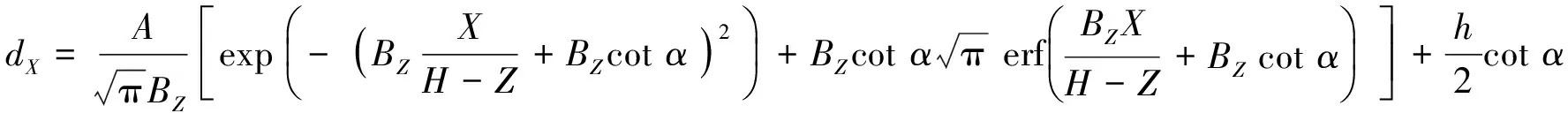
因此， 不排水条件下正断层错动引起的上覆粘土变形方程为：

和

1.4 地表及地下土体变形曲线

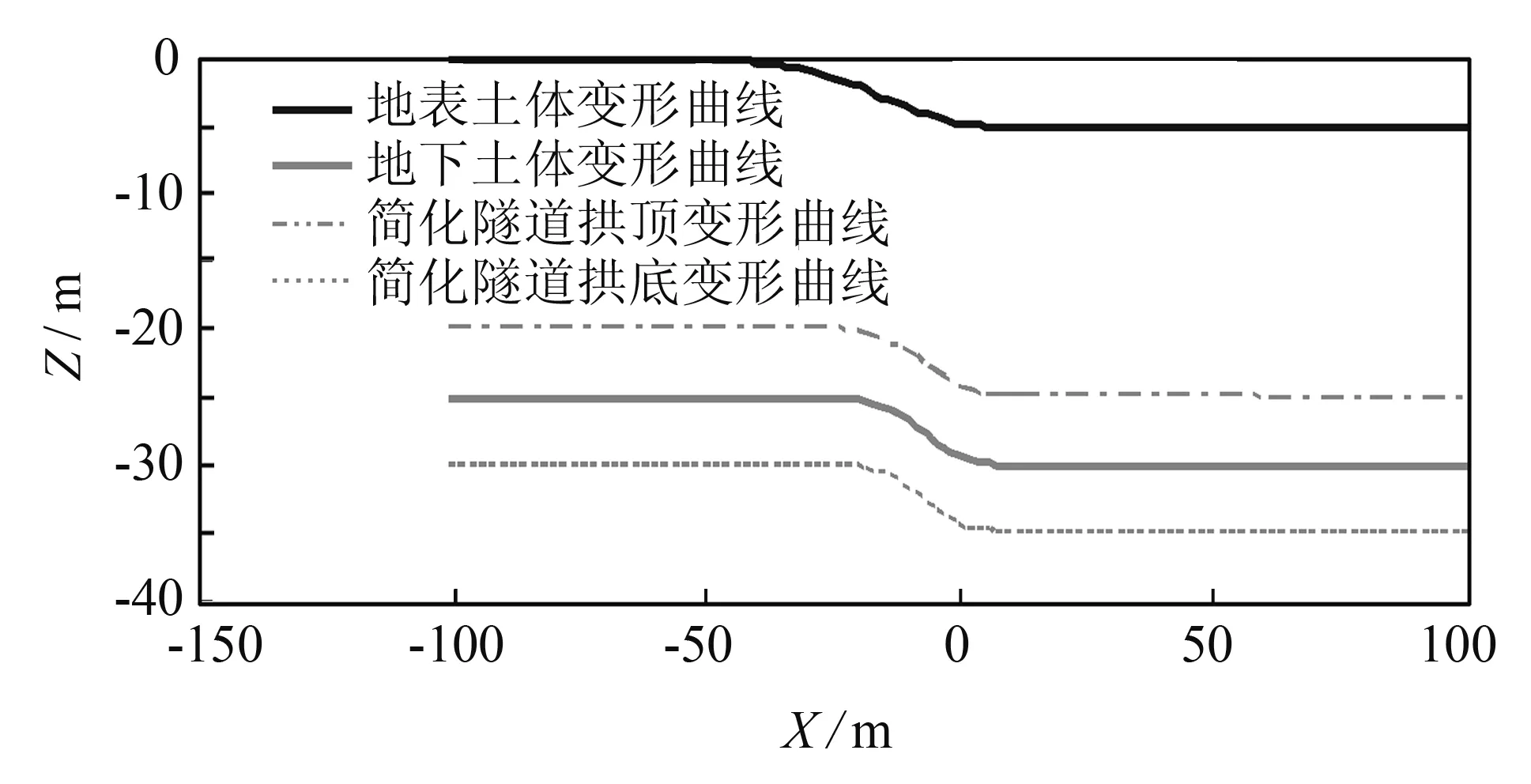
图2 地表及地下土体的变形曲线Fig.2 Ground and under ground deformation

公式(7)、 (8)可用于计算地表及地下土体的水平向和竖向位移. 例如， 取一上覆土层厚度 、 基岩断层倾角、 基岩正断层错动量、 土体埋深Z分别取0和25 m. 图2中深色和灰色实线分别为计算得到的地表和地表以下25 m处土体的变形曲线. 从图中可以看出， 基岩正断层错动引起地表土体变形集中在离开基岩断层水平距离-40～10 m， 25 m深处的地下土体变形则主要集中在-25～0 m. 图2中计算得到的土体变形特征符合图1所示的变形机理， 即土体变形主要集中在剪切区域， 且土体剪切区域的宽度随深度增加而减小.

2 隧道变形预测

2.1 隧道变形预测模型的建立

对于地表以下Z深度处的隧道(以隧道轴线位置计)， 当基岩正断层错动量较小时， 可假设隧道与原有土层变形在竖直方向趋于一致， 即隧道轴线处的竖向变形与相应土层的竖向变形处处相等. 由此， 不排水粘土中正断层错动引起的隧道竖向变形可根据上述方程(7)计算. 图2中虚线给出了隧道拱顶和隧道拱底变形示意图.

由于隧道的高跨比较小， 可假定隧道变形符合平面假设.

其中：L为隧道衬砌离开隧道轴线的竖向距离； dθ为从隧道中截取的长为dX的单元体左右两横截面的相对旋转角度.

在小变形情况下， 隧道的挠度远小于其长度， 隧道变形后的轴线是一条平坦的曲线. 此外， 横截面形心沿X轴方向的线位移与挠度相比属于高阶微量， 可略去不计. 因此， 离开隧道轴线高度为L处的衬砌纵向线应变为：

将方程式(7)代入方程式(10)求导得：

对于隧道拱顶、 拱底处的L分别为R和-R， 从而拱顶和拱底衬砌的纵向线应变分别为：

和

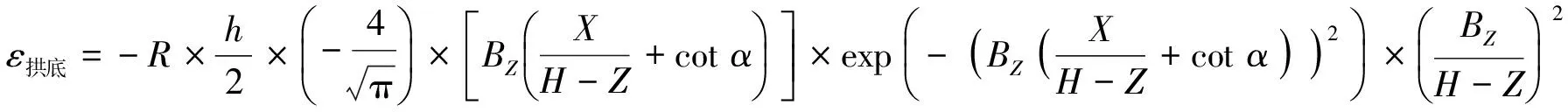
2.2 隧道变形计算实例

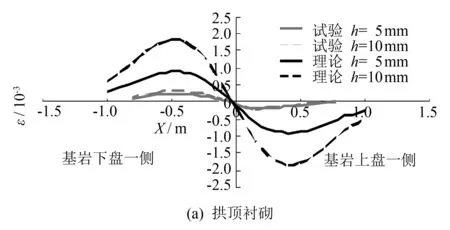
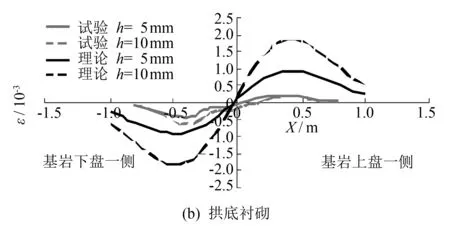
图3 隧道纵向应变分布曲线

图3(a)中的理论和试验数据均表明， 在正断层错动影响下， 隧道拱顶衬砌在基岩下盘一侧受拉， 在基岩上盘一侧则表现为受压.Anastasopoulos等[4]和熊炜等[5]对正断层错动引起隧道变形的数值研究中同样发现类似的破坏特征. 计算结果表明， 在相同的错动量下， 受压区和受拉区的应变峰值和分布范围相当. 随着断层错动量的增加， 衬砌受拉区和受压区的应变峰值均逐渐增大. 如图3(b)所示， 隧道拱底衬砌则呈现出与拱顶不同的应变分布. 拱底衬砌在基岩下盘一侧以受压为主， 在基岩上盘一侧则表现为受拉. 由于混凝土的拉裂应变往往小于相应的压裂应变， 隧道在断层错动影响下会先呈现拉裂破坏. 对比图3(a)和3(b)还可以发现， 无论是隧道拱顶还是隧道拱底， 其受拉区的范围受错动量的影响并不明显. 由此， 本理论模型可用于确定隧道针对拉裂破坏需要进行加固的范围. 值得注意的是， 图3中的理论计算结果相比试验数据偏大， 这可能是由于理论计算模型假定隧道与土体竖向变形一致， 而忽略隧道刚度对自身变形的影响.

对于汶川地震， 虽然以逆断层错动为主， 不同于本文的正断层错动， 但现场的隧道震害统计发现， 洞身段震害主要发生在拱部和仰拱[2]， 这与本文分析结果表明拱顶和拱底衬砌会发生拉裂破坏是一致. 进一步对比逆断层错动引起隧道破坏的模型试验表明， 逆断层错动引起拱顶拉裂破坏区域偏向断层上盘一侧， 而拱底拉裂破坏区域则偏向断层下盘一侧[6]. 由此可见， 由逆断层引起的隧道拉裂破坏区的分布规律与正断层引起的分布规律不同.

2.3 隧道加固区域计算

由图3分析可知， 基岩断层错动会引起隧道衬砌结构的拉裂破坏. 拉裂破坏区域的分布受衬砌离开隧道轴线高度的影响. 为了进一步利用本计算模型确定隧道拉裂破坏加固区域， 现以一理想隧道为基本算例， 采用公式(11)计算不同高度处隧道衬砌的纵向线应变分布. 假定上覆饱和粘土厚度为50m， 半径为5m的隧道埋置于地表以下25m深度处. 基岩断层与隧道轴线正交， 断层倾角为70°. 根据文献研究，Bray等[13]认为基岩断层的错动量上限介于1到5m之间. 为对比基岩错动量对拉裂破坏区域的影响， 断层错动竖向分量取为0.5和5m. 对于饱和粘土可取形状参数BZ为3.04[8]. 进一步假定隧道衬砌的极限拉应变为75×10-6， 则由公式(11)可计算不同高度处隧道衬砌出现拉裂破坏的分布区域， 从而为隧道加固区域提供理论依据. 图4阴影部份给出了计算得到的隧道拉裂破坏区域.

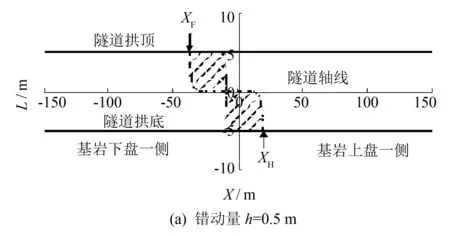
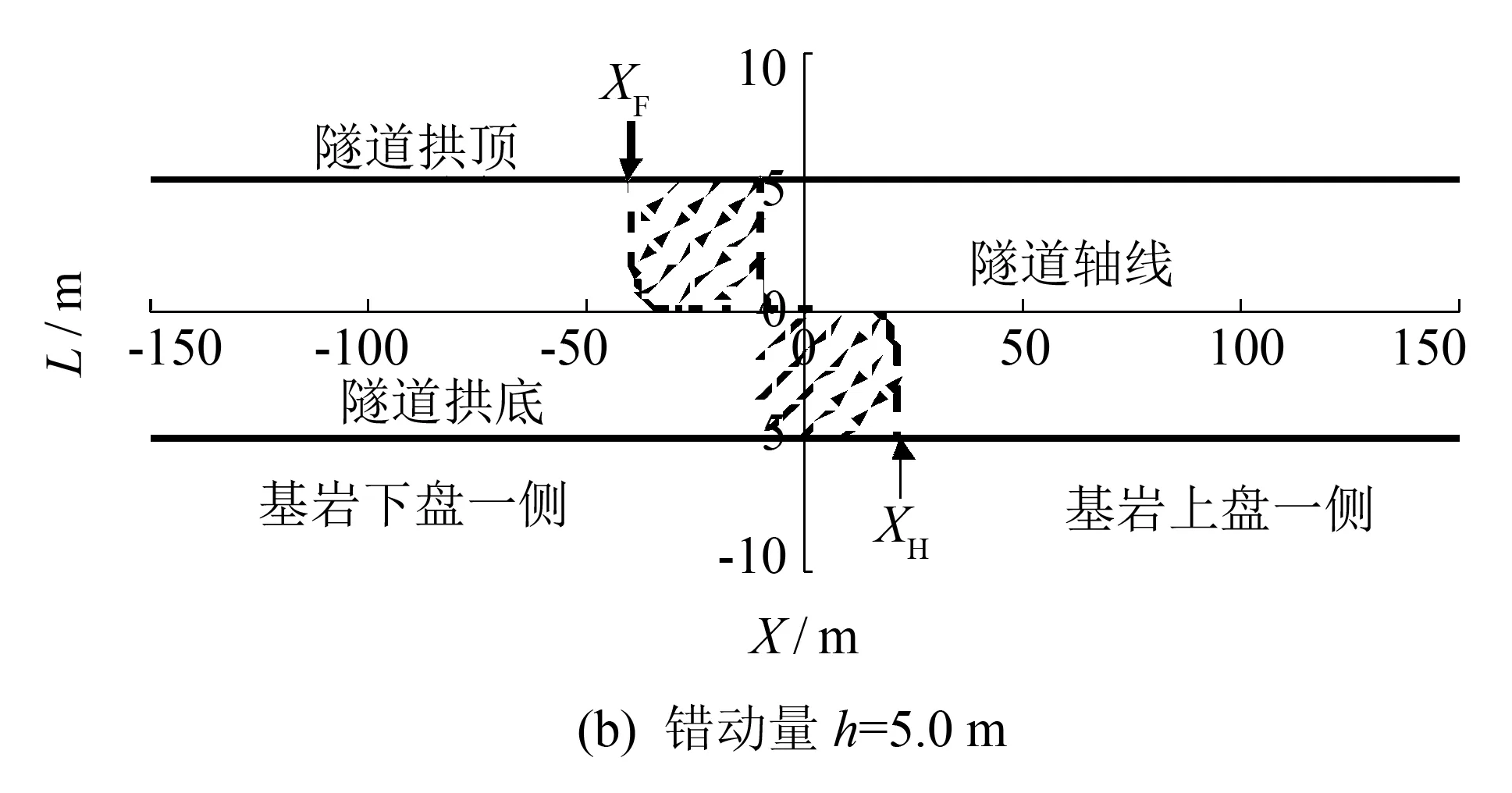
(XF为拱顶拉裂破坏区域靠近基岩下盘一侧边界， XH为拱底拉裂破坏区域靠近基岩上盘一侧边界)

由图4(a)可知当基岩错动量为0.5 m时， 隧道衬砌在基岩下盘一侧的拉裂破坏区域位于隧道轴线以上， 而在基岩上盘一侧则位于隧道轴线以下. 在隧道拱顶和隧道拱底形成的拉裂破坏区域宽度基本一致， 约为30 m. 此外， 两个拉裂破坏区域的宽度受衬砌离开隧道轴线竖向距离的影响并不显著. 但对于靠近隧道轴线处的衬砌， 拉裂破坏区域的宽度急剧缩小. 这是由于理论计算模型假定隧道变形符合平面假设， 隧道轴线高度处衬砌的纵向线应变为零. 图4(b)中， 基岩错动量虽增加至5.0 m， 隧道拉裂破坏区域的分布规律与小错动量下的分布规律基本一致. 对比图4(a)和(b)还可以发现， 隧道拱顶和拱底的拉裂破坏区域宽度受基岩断层错动量的影响并不显著.

基于上述分析， 为提高隧道在断层活动中抵抗拉裂破坏的能力， 可对图4所示的潜在拉裂破坏区域进行加固. 为了便于工程操作， 可取拱顶拉裂破坏区域靠近基岩下盘一侧边界(XF)和拱底拉裂破坏区域靠近基岩上盘一侧边界(XH)作为加固区域的两个边界. 对于新建隧道， 可对加固边界XF和XH内的衬砌提高配筋等级进行加固. 对于既有隧道， 可在加固边界XF和XH内进行植筋加固[14-15]. 由于本研究从隧道变形符合平面应变假定出发， 关注隧道变形区域的分布特征， 暂未能考虑地铁隧道的结构特性和构造特点的影响， 相关研究需要进一步展开.

3 隧道变形关键影响参数分析

为了进一步考察理论计算模型， 现以上述基本算例为研究对象， 改变隧道埋深和断层倾角两个关键参数， 计算隧道衬砌的纵向线应变. 由图4已知， 隧道拉裂破坏区域基本不受基岩断层错动量的影响. 因此， 在下列分析中均采用基岩断层错动量h=0.5 m. 同样假定隧道衬砌的极限拉应变为75×10-6.

3.1 隧道埋深的影响规律

图5给出了在断层倾角为70°时， 隧道埋深Z(以隧道轴线埋深计)对隧道拉裂破坏加固区域的影响. 由图5可以看到， 随着隧道埋深的增加， 需要加固的区域逐渐缩小. 这与图1中所揭示的上覆土体变形机理相一致. 土体主要变形区域(剪切区域)的宽度随埋深的增加而减小， 从而使得隧道的破坏区域随埋深的增加而集中于基岩断层附近. 根据土体变形计算公式(7)， 土体变形曲线拐点(即土体剪切变形最严重的位置)位于基岩断层延长线上(X=-cotα·(H-Z)). 图5中虚线给出了不同隧道埋置深度处的土体变形曲线拐点位置. 可以看出， 隧道拉裂破坏加固区域对称分布于曲线拐点两侧. 此外加固区域随隧道埋深的增加而偏向基岩上盘一侧， 符合土体变形曲线拐点随深度的变化趋势.

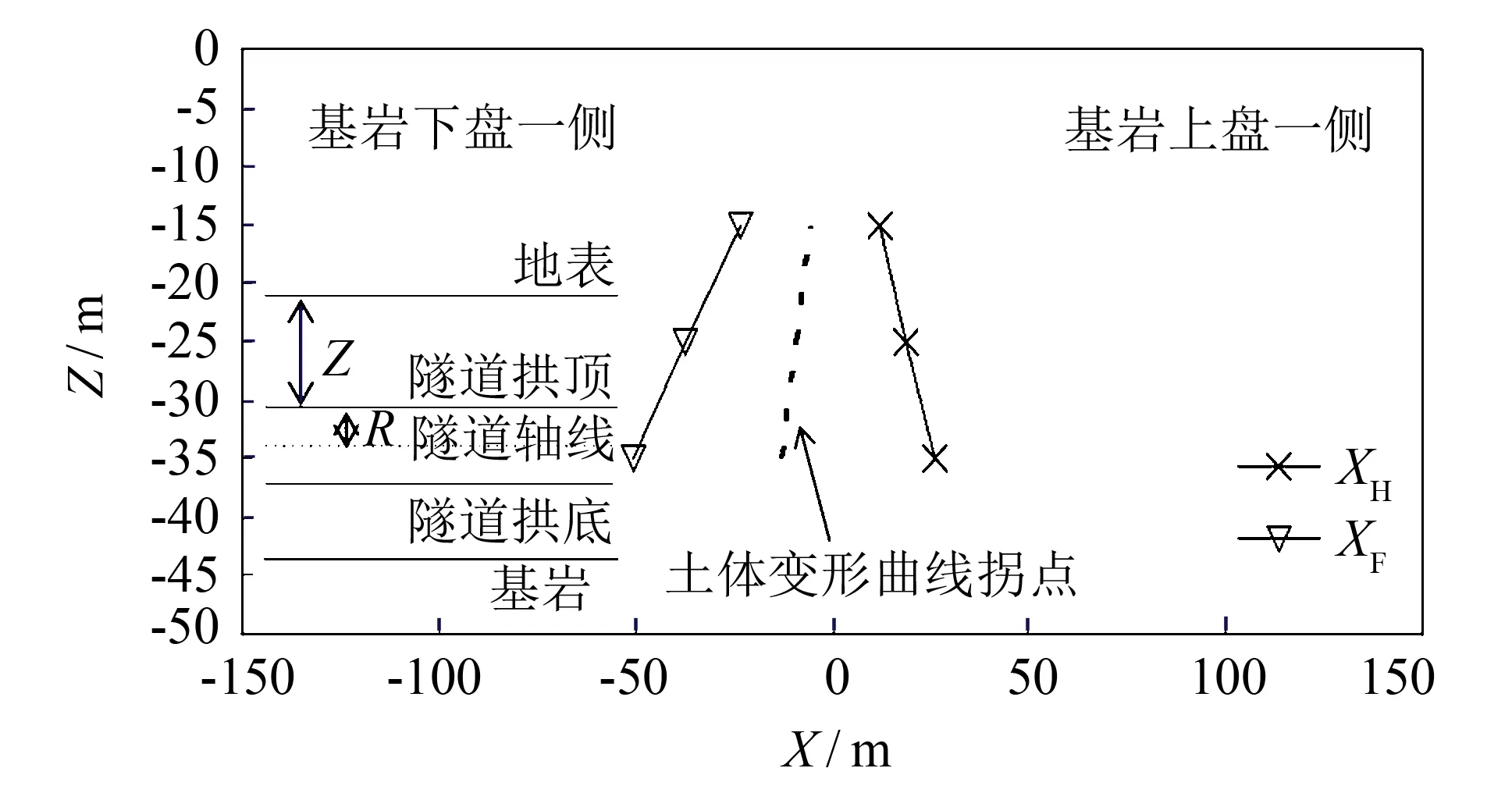
图5 隧道埋深对隧道拉裂破坏加固区域的影响Fig.5 The effects of tunneling depth on width of reinforcing zone

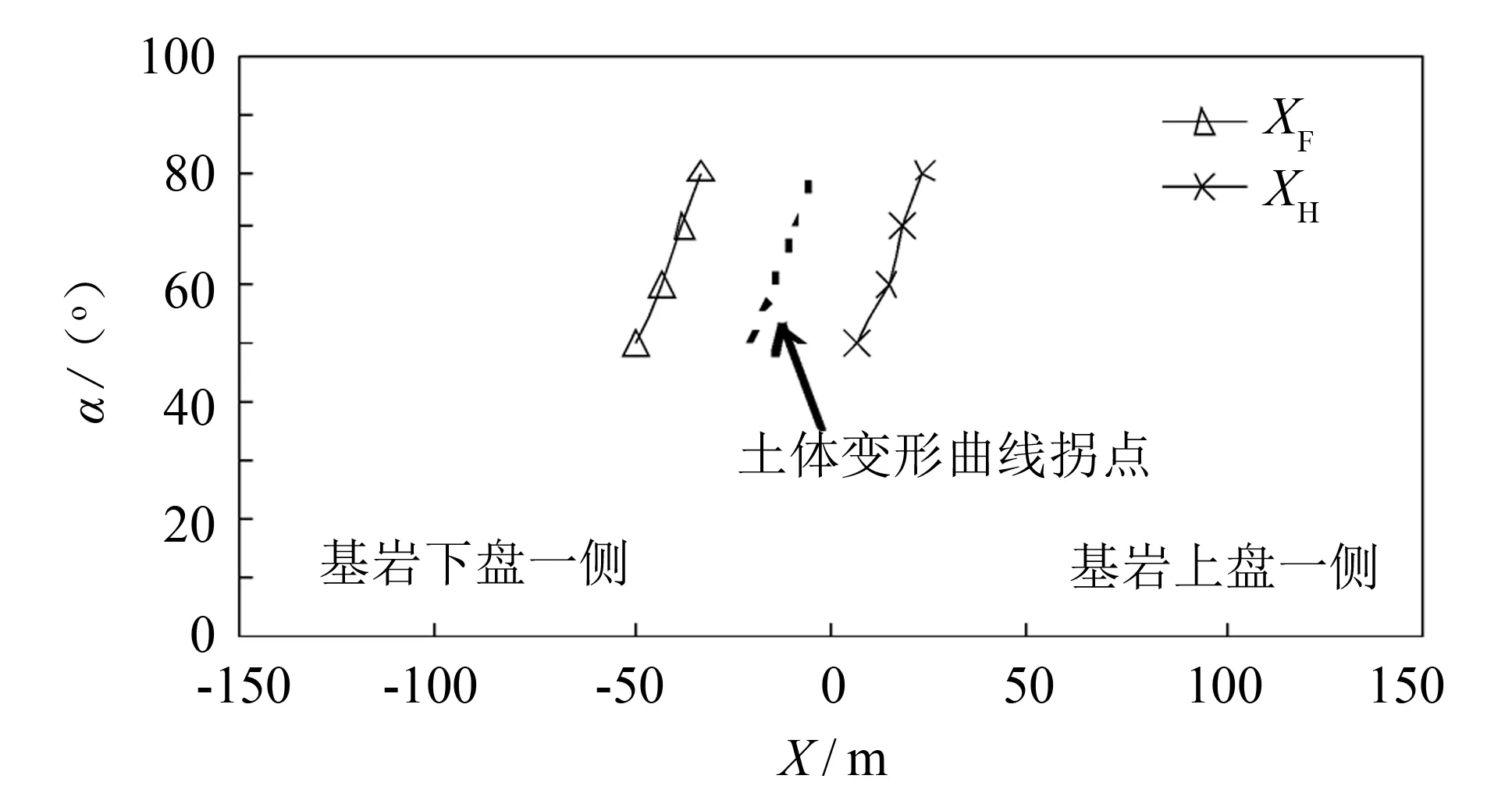
图6 断层倾角对隧道拉裂破坏加固区域的影响Fig.6 The effects of dip angel of normal fault on width of reinforcing zone

3.2 断层倾角的影响规律

图6给出了在同一隧道埋深情况下(Z=25 m)， 断层倾角对隧道拉裂破坏加固区域的影响. 由图6可以看到， 随着基岩断层倾角的增加， 隧道拉裂破坏加固区域向基岩上盘一侧偏移. 图6中虚线给出了不同倾角下， 隧道埋置深度处的土体变形曲线拐点的位置. 同样可以看出， 隧道主要加固区域对称分布于变形曲线拐点两侧. 隧道加固区域的大小范围受断层倾角的影响并不显著.

4 结语

基于正断层错动引起的上覆土体变形规律， 建立上覆土体中地铁隧道变形的理论计算模型， 为地铁隧道的断层效应防治提供了理论依据. 在结合试验数据验证的基础上， 进一步研究了隧道埋深、 断层倾角两个关键因素的影响规律， 得到了以下主要结论：

1) 根据理论计算模型分析， 影响隧道拱顶、 拱底的纵向线应变的参数有： 隧道半径R， 土层厚度H， 基岩断层错动量h， 断层倾角α， 隧道埋置深度Z(按隧道轴线埋深计)和形状参数BZ. 根据本文建立的计算模型， 这些影响因素得以量化分析.

2) 在正断层错动影响下， 隧道拱顶衬砌分别在基岩下盘和基岩上盘一侧出现受拉区和受压区. 而隧道拱底衬砌则相反， 分别在基岩下盘和基岩上盘一侧出现受压区和受拉区. 但无论是拱顶还是拱底， 拉裂破坏区域宽度受基岩断层错动量的影响并不显著.

3) 针对隧道埋深关键因素的参数分析表明， 随着隧道埋深的增加， 需要进行拉裂破坏加固的区域逐渐缩小， 并向基岩断层趋于集中.

4) 针对断层倾角关键因素的参数分析表明， 随着基岩断层倾角的增加， 隧道拉裂破坏加固区域往基岩上盘一侧偏移. 但加固区域的大小范围受断层倾角的影响并不显著.

[1] 刘学增， 滨田政则. 活断层破坏在土体中传播的试验研究[J]. 岩土工程学报， 2004， 26(3)： 425-427.

[2] 崔光耀， 王明年， 林国进， 等. 汶川地震区典型公路隧道衬砌震害类型统计分析[J]. 中国地质灾害与防治学报， 2011， 22(1)： 122-127.

[3] 郝建斌， 门玉明， 李凯玲. 地铁隧道正交穿越地裂缝的结构变形预测[J]. 广西大学学报： 自然科学版， 2011， 36(1)： 128-131.

[4] Anastasopoulos I, Gerolymos N, Drosos V,etal. Behavior of deep immersed tunnel under combined normal fault rupture deformation and subsequent seismic shaking[J]. Bulletin of Earthquake Engineering， 2008， 6(2)： 213-239.

[5] 熊炜， 范文， 彭建兵， 等. 正断层活动对公路山岭隧道工程影响的数值分析[J]. 岩石力学与工程学报， 2010， 29(增刊1)： 2 845-2 852.

[6] 刘学增， 林亮伦. 75°角逆断层黏滑错动对公路隧道影响的模型试验研究[J]. 岩石力学与工程学报， 2011， 30(12)： 2 523-2 530.

[7] 黄强兵， 彭建兵， 高虎艳， 等. 地铁隧道斜交穿越地裂缝带的纵向设防长度[J]. 铁道学报， 2010， 32(1)： 73-78.

[8] Cai Q P， Ng C W W. Analytical approach for estimating ground deformation profile induced by normal faulting in undrained clay[J]. Canadian Geotechnical Journal， 2013， 50(4)： 413-422.

[9] Faccioli E, Anastasopoulos I, Gazetas G,etal. Fault rupture-foundation interaction: selected case histories[J]. Bulletin of Earthquake Engineering， 2008， 6(4)： 557-583.

[10] Roboski J， Finno R J. Distributions of ground movements parallel to deep excavations in clay[J]. Canadian Geotechnical Journal， 2006， 43(1)： 43-58.

[11] Cai Q P， Huang Y, Meng F Y. Normalized soil deformation induced by underlying bedrock fault[J]. Advanced Materials Research， 2013， 790： 150-154.

[12] 李凯玲， 门玉明， 严静平， 等. 地铁隧道正交穿越地裂缝的相互作用机制试验研究[J]. 岩石力学与工程学报， 2011， 30(3)： 556-563.

[13] Bray J D， Seed R B， Cluff L S，etal. Earthquake fault rupture propagation through soil[J]. Journal of Geotechnical Engineering， 1994， 120(3)： 543-561.

[14] 胡奕东， 郭子雄， 柴振岭， 等. 嵌缝加固条石砌筑石墙的抗震性能初探[J]. 工程抗震与加固改造， 2009， 31(6)： 24-27.

[15] 蒋程， 管东芝， 邢晨曦， 等. 植筋连接混凝土梁抗剪承载力试验研究[J]. 建筑技术， 2011， 42(7)： 653-654.

(责任编辑： 沈芸)

Theoretical model for calculation of subway deformation induced by normal faulting

HUANG Yun1， CAI Qipeng1， GUO Zixiong1， GUO Liqun1， SU Shizhuo2， CHEN Xingxin1

(1. College of Civil Engineering， Huaqiao University， Xiamen， Fujian 361021， China；2. Architectural Design Institute， Huaqiao University， Quanzhou， Fujian 362021， China)

There is no a theoretical model for deformation prediction of subway tunneling induced by normal faulting. Based on the deformation mechanism of overlying soil under a undrained condition, a theoretical model was developed to calculate deformation of subway tunneling. This theoretical model show that the main influencing factor includes radius of tunnel, soil thickness, magnitude of bedrock fault movement, dip angle of bedrock fault, depth of the tunnel and a shape parameter. After normal faulting, a tensile zone and a compressive zone were observed at the crown of the lining on the side of foot wall and hanging wall, respectively. Regarding the invert of the lining, the compressive zone and the tensile zone were observed on the side of foot wall and hanging wall, respectively. With the increase in depth of tunnel, the width of reinforcing zone of lining was reduced and localized around bedrock fault. With increase in dip angel of bedrock fault, enhancing zone of lining moved towards the side of hanging wall with almost the same width.

normal faulting； subway； tunneling； theoretical model

10.7631/issn.1000-2243.2015.04.0523

1000-2243(2015)04-0523-07

2014-02-26

蔡奇鹏(1982-)， 讲师， 博士， 主要从事岩土与隧道工程研究， cqp@hqu.edu.cn

国家自然科学基金资助项目(51208218)； 中国博士后科学基金资助项目(2013M541854, 2014T70608)； 福建省自然科学基金资助项目(2014J01194)

U45

A