Two-Dimensional Terahertz Time-Domain Spectroscopy and Its Applications

Jia-Yu Zhao and Wei-Wei Liu

Two-Dimensional Terahertz Time-Domain Spectroscopy and Its Applications

Jia-Yu Zhao and Wei-Wei Liu

—In this work, we review the developing progress of two-dimensional terahertz time-domain spectroscopy (THz-TDS) and its diverse applications, including analyzing the polarization of THz radiation from a laser-induced plasma source and studying the corresponding physical mechanism, and characterizing the optical properties of crystals, etc.

Index Terms—Application, laser-induced plasma, optical property, physical mechanism, polarization, two-dimensional terahertz time-domain spectroscopy.

1. Introduction

In recent decades, terahertz (THz) science and technology have become a cutting-edge research topic attracting intense interest from all over the world[1]. THz wave, with frequencies in the range of 0.1 THz to 10 THz, can be coherently detected by the means of THz time-domain spectroscopy (TDS)[2]–[16], allowing measurement of the transient electric field, not only its intensity. THz-TDS was first reported by Austonet al.[2]in 1984 for the detection of THz radiation via photoconductive antenna (PCA). Later in 1995 to 1996, THz detection by free space electro-optic sampling (EOS) was realized due to significant efforts of Nahataet al.[3], Jepsenet al.[4], and Wuet al.[5].

A typical characteristic of a traditional THz-TDS is that only one component of the electric field vector is measured, which is usually not enough, for example, in the case of understanding the optical properties of birefringent materials. In order to obtain full information of THz waves, it is necessary to measure the orthogonal electric field components of a THz pulse. Therefore, two-dimensional THz-TDS is gradually developed[6]–[16]. Being able tomeasure the polarization state of THz radiation, twodimensional THz-TDS is suitable for studying the anisotropic responses of materials induced by factors such as structure, stress, and electromagnetic fields[17], and characterization and identification of chemicals and biological materials which have spectral features within the THz region[18].

2. Developing Progress of Two-Dimensional THz-TDS

Among various kinds of two-dimensional THz-TDS, the most obvious approach may be the use of a THz linear polarizer, e.g., a wire grid, being able to be rotated after the sample, to selectively measure the horizontal and vertical THz electric field components, respectively[6]. Similarly, a rotation of a conventional (two-contact, single metal slit) PCA, which acts as the detector of the THz-TDS, has almost the same effect[7], that is, measuring one THz electric field component, then rotating the PCA receiver by 90 degree, and measuring the orthogonal component. What’s more, a heterodyne detection system, which itself acts as a THz linear polarizer[6], could be used as a THz detector to measure the THz components polarized along two orthogonal axes at approximately 0.1 THz[8].

However, in practice, the rudimentary two-dimensional THz-TDS mentioned above has two major disadvantages[19]: firstly, the rotation of the THz linear polarizer or the PCA receiver may result in slight optical path misalignment, which will shift the relative phase of the orthogonal THz electric field components; secondly, the THz signal acquisition time is doubled because both components are separately recorded.

Alternatively, simultaneous measurement of two THz polarization components seems to be a better choice than sequential detections. One can simultaneously record two THz orthogonal components by splitting the THz polarizations to two separate PCA detectors, oriented by 90 degree to each other[9]. Similarly, the use of a dual EOS detection scheme was reported by [10], in which the split horizontal and vertical THz components are independently measured by two identical EOS systems.

A rather convenient way to simultaneously detect two orthogonal THz polarization components is the use of a multi-contact PCA receiver[11]–[15], which has more than one metal slit to detect multi-THz polarization components, without additionally splitting the THz beam. For example, a three-contact PCA[11],[12]with a pair of orthogonal metalslits is able to simultaneously measure two orthogonal electric field components of an arbitrary polarized THz wave. Moreover, an improved THz air-biasedcoherent-detection (THz-ABCD)[16], by providing an orientation-modulated bias field at the focus of the probe beam with two orthogonally arranged pairs of electrodes, could also be a polarization-sensitive scheme to directly measure the amplitude and polarization angle of THz electric field in the time domain.

Comparing THz-TDS by means of EOS and PCA, [20]–[22] have suggested the THz pulse is best detected via free space EOS rather than with PCA when using an amplified laser system. One may also notice the significant THz signals differences between EOS and PCA[23]–[25], due to the carrier lifetime of the PCA material and the frequency dependent response of the PCA receiver[23]. Furthermore, EOS is preferred[26]because of its simplicity and spectral broadness for the broadband detection of THz pulse, compared with the PCA technique.

Hence, in this work, we focus on the EOS based twodimensional THz-TDS. A traditional THz-TDS via freespace EOS requires that the THz field is focused onto an EO detection crystal. As the optical probe pulse passes through the EO crystal, its polarization is rotated according to the birefringence induced by the electric field of the THz pulse at that time. The relatively long THz pulse (～1 ps) is coherently reconstructed by sweeping the relative time delay of the much shorter optical probe pulse (～50 fs) throughout the duration of the THz waveform. For two-dimensional THz-TDS measurement, a THz polarizer, e.g., a wire grid, is generally inserted in the THz beam path for high transmission of THz wave along the wire grid’s polarization axis. In order to measure the orthogonal polarized THz component, the wire grid, EO crystal, and polarization of the probe beam are all needed to be rotated by 90 degree[27].

The abovementioned disadvantages, i.e., the alignment errors and the long data acquisition time, could be overcome by a technique based on the fast mechanical rotation of EO crystal and lock-in detection, allowing for stable, precise, and fast two-dimensional TDS measurement of a THz wave[28],[29].

3. Applications of Two-Dimensional THz-TDS

3.1 Analysis of Polarization of THz Radiation from a Laser-Induced Plasma Source

Two-dimensional THz-TDS can be used to investigate the polarization of THz emission during filamentation. In the single-color case, a wire grid linear polarizer was used in front of a heterodyne detection system[6]. By rotating the wire grid, the amplitude of the THz signal as a function of the wire grid polarization angle was measured, and radially linear polarization at around 0.1 THz was suggested[6]. In the two-color case, however, the results are more complicated. There are two points of view raised by Zhanget al.[27], Chenet al.[30],and Dietzeet al.[31]that the THz wave could be considered as linear[27]or elliptical polarized[30],[31].

Firstly, in 2009, Zhanget al.[27]confirmed that in the commonly used two-color laser mixing experiment, the generated THz wave in air is mainly linearly polarized, as shown in Fig. 1, and its predominant polarization direction is orthogonal to that of the second harmonic. They achieved this conclusion by using the experimental configurations of EOS as shown in Fig. 2. The generated THz pulse was focused onto a (110)-oriented ZnTe crystal. A wire grid polarizer was inserted in the THz beam path. The probe beam was combined with a THz pulse by a pellicle beam splitter to perform EOS measurement. TheXaxis and theYaxis were along the horizontal and vertical directions, respectively. For measuring theX-polarized THz component, the rotation angle of the wire grid was optimized for high transmission of theX-polarized THz wave, under which circumstance, the polarization of the probe beam was also parallel to theXaxis. And the (001) axis of the (110)-oriented ZnTe crystal was set to be perpendicular to theXaxis[32]. For measuring theY-polarized THz component, the wire grid, probe beam polarization, and ZnTe crystal were all rotated by 90 degree. That is, the (001) axis of the ZnTe crystal and the polarization of the probe were needed to be rotated in accordance with the rotation of the wire grid to minimize the orientation dependence of THz pulse detection in the ZnTe crystal[30],[32].

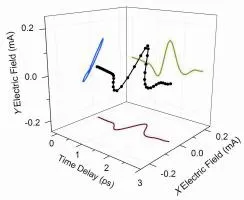
Fig. 1. A representative THz electric field trajectory (line with solid circles) and its predominant polarization direction (line in theX-Yplane).

Then, in the same year, Chenet al.[30]and Dietzeet al.[31]analyzed the polarization of the THz pulse emitted from the two-color filament in the similar way as Zhanget al.[27]did. They both mounted the EO crystal on a rotation stage, which allowed them to measure theX- andY-components of the THz electric field independently. Especially, Chenet al.also placed a wire grid polarizer before the ZnTe crystal for a better polarization analysis. Different from Zhanget al., however, Chenet al.and Dietzeet al.demonstrated the elliptical polarized THz wave. These two different experimental observations have made the THz polarization from two-color filament remain fuzzy.

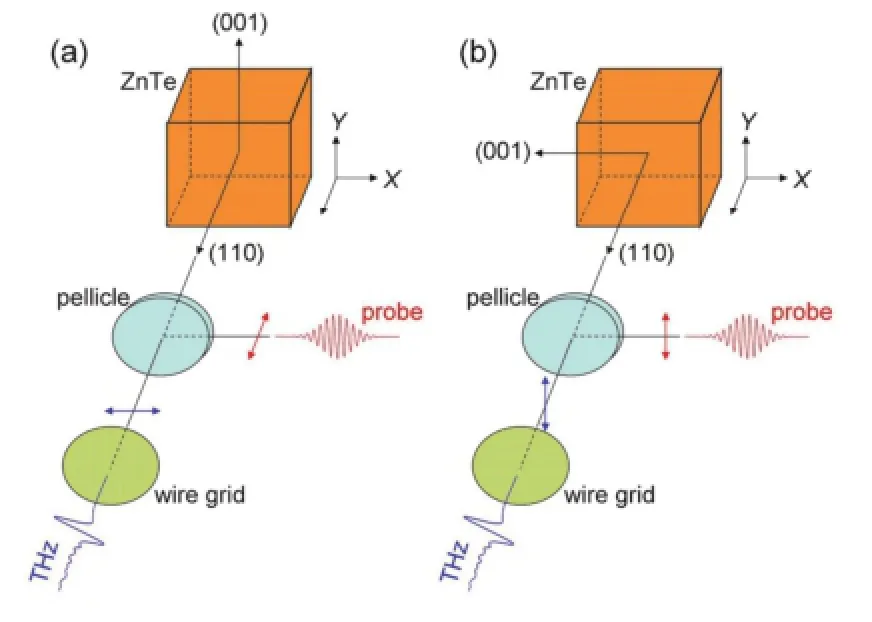
Fig. 2. Wire grid, ZnTe crystal and probe polarization were rotated by 90 degree to measure the two orthogonal components of the THz electric field: (a) for measuring theX-polarized THz component, the (001) axis of ZnTe crystal and probe polarization is vertical and horizontal, respectively and (b) for measuring theY-polarized THz component, the (001) axis of ZnTe crystal and probe polarization is horizontal and vertical, respectively.

Later in 2013, with the similar EOS detection scheme shown in Fig. 2, Youet al.[33]seemed to bridge these two different ideas: the THz polarization could evolve from linear to elliptical with increasing plasma length, which was controlled by a 2-mm aperture scanned along the plasma filament. With even longer plasma filament generated by accurate control of the two-color filament surrounding gas pressure, Manceauet al.[34]even obtained circularly polarized THz pulses. During their experiment, the filament radius decreased with an increase of the surrounding gas pressure, while the length of the filament extended as the gas pressure increased. The emitted THz radiation was collected and refocused onto a thermal pyroelectric detector, before which a THz polarizer was used to conduct the polarization analysis.

It is worth mentioning that, the EOS sensitivity depends on the polarization of incident THz waves and the orientation of the EO crystal[32],[35],[36], and thus an EO crystal could be regarded as a polarization-sensitive THz detector[36]–[39]. That is, for a certain EO crystal orientation, only the desired THz polarization component produces a signal[40]–[42]. Hence, when performing two-dimensional THz-TDS measurement, an appropriate rotation of the crystallographic axis of the EO crystal to maximize the desired THz polarization component signal is necessary. As mentioned before, for a (110)-oriented ZnTe crystal, the (001) axis of ZnTe crystal should always be set to be perpendicular to the coming THz polarization component, which is usually projected onto the polarization axis of a wire-grid polarizer. The relative orientations of these two optical devices, i.e., EO crystal and THz linear polarizer, should always be kept the same to ensure a constant response in EOS system for THz components with any polarization.

However, to the best of our knowledge, not all the previous reports have paid enough attention to this point. Either their EO crystals are held fixed[43],[44], or there is little information describing their detection principle details[45]. On the other hand, even if one adopts PCA based THz-TDS to measure polarization dependent THz signals, it is also crucial to rotate the PCA receiver[46], after the rotation of the THz linear polarizer. No rotation of the EO crystal or the PCA receiver may lead to quantitative errors of the recorded THz amplitude and wrong polarization angle of THz electric field.

3.2 Study of Physical Mechanism of THz Radiation from a Laser-Induced Plasma Source

Achieving the polarization of THz emission during filamentation by two-dimensional THz-TDS, one can further investigate the underlying physical mechanisms of THz emission from a laser-induced plasma source. The mechanism of the reported radially polarized THz pulse generation[6], in the case of single-color laser field pumping scheme, has been generally understood as the transition Cherenkov emission from the plasma space charge moving behind the ionization front at light velocity[6]. In two-color case, however, different points of view have been brought forward to explain the polarizations of the generated THz pulse.

As for the linearly polarized THz wave, Zhanget al.[27]have confirmed that the theoretical calculation based on the four-wave mixing could reproduce the experimental results, as shown in Fig. 3. Open circles in Fig. 3 (a) and open triangles in Fig. 3 (b) are experimental results of the peak-to-peak amplitudes ofETHz,XandETHz,Y, respectively.θis the rotation angle of the BBO crystal, which is defined as the angle between theXaxis and the extraordinary refractive index axis (eaxis) of the BBO crystal. The solid lines in Fig. 3 (a) and (b), given by analytic expressions in (1):

are used to fit the experimental results. Equation (1) is deduced from the four-wave mixing model, whereais a proportionality factor containing the nonlinear susceptibility tensor related to the four-wave mixing process, andEωis the electric field of the input pump beam. It can be seen that the fitting curves closely follow the measurement data.

In this article, we have further tried the well-known photocurrent model[47]in order to provide a basis for the linear polarized THz pulse generated in Zhang’s work. By projectingETHz,X(θ) andETHz,Y(θ) onto theoandeaxes of the BBO crystal,ETHz,o(θ) andETHz,e(θ) can be retrieved by

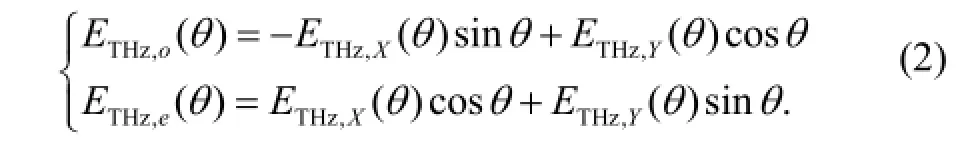
The peak-to-peak amplitude ofETHz,oandETHz,eare shown as open circles in Fig. 4 (a) and open triangles in Fig. 4 (b), respectively. The fitting solid lines in Fig. 4 are simulated based on the photocurrent model[47]. The experimental parameters in Zhang’s work were adopted as the initial parameter of the simulations.

Fig. 3. Variation of THz peak-to-peak amplitude as a function ofθ: (a)ETHz,X(open circles). The solid line is calculated according to (1) and (b) the same as (a) forETHz,Y(open triangles).

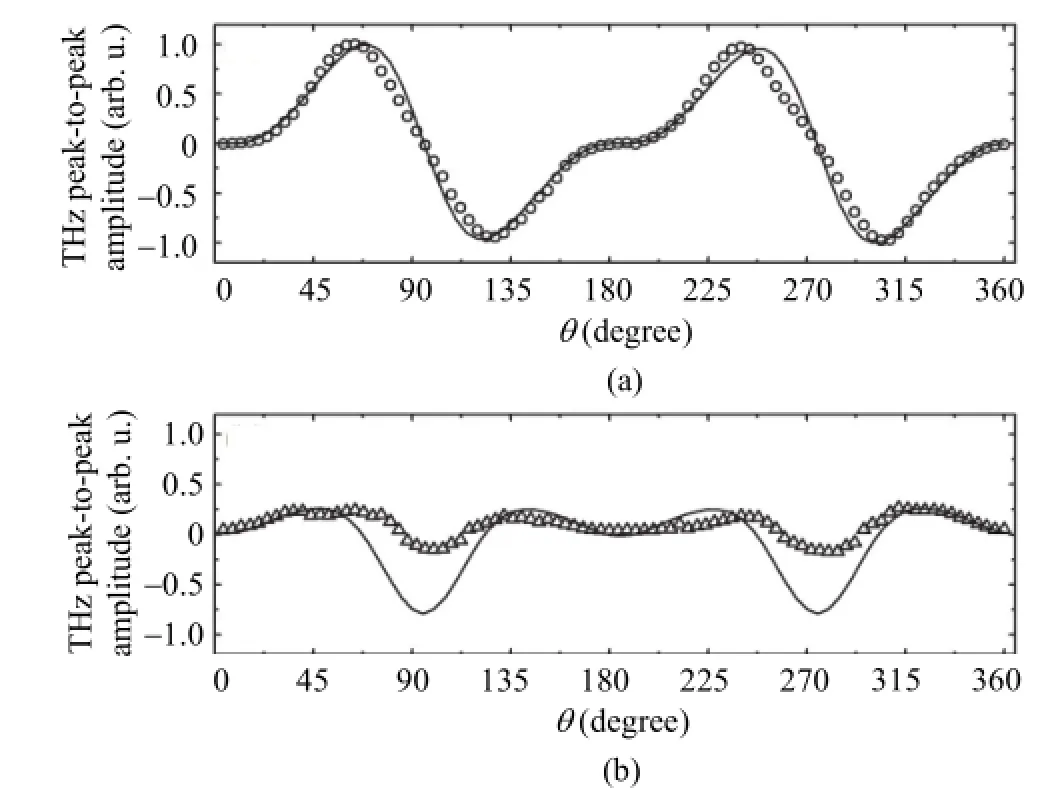
Fig. 4. Variation of THz peak-to-peak amplitude as a function ofθ: (a)ETHz,o(open circles). The solid line is simulated according to the photocurrent model and (b) the same as (a) forETHz,e(open triangles).

On the other hand, whenθwas varied, the nitrogen (N2) fluorescence signal at 337 nm, which was emitted from the plasma column, has also been collected by a fused silica lens onto a photomultiplier tube (PMT)[48]. The strength of theN2fluorescence signal, which is a good indication of the free electron density (Ne)[49], is depicted in Fig. 5 as the open circles, and the fitting result (solid line) is given by the static tunneling ionization model[50].

After carefully reading Fig. 4 and Fig. 5, one can see an obvious discrepancy located in the vicinity ofθ= 90 and 270 degree, where the experimental peak-to-peak amplitude ofETHz,eis much smaller than that of simulation (Fig. 4 (b)), and the maximums ofNe(θ) are also recorded atθ= 90 and 270 degree (Fig. 5). These observations guide us to pay attention to the correlation between the evolution of peak-to-peak amplitude ofETHz,e(θ) andNe(θ), and a question is naturally raised: could it be possible that the interaction between THz wave and plasma results in the inconsistence shown in Fig. 4 (b), since it has been suggested that THz wave could propagate inside plasma filament[51],[52]. An extension of the photocurrent model including the propagation effect of the THz pulse during the filamentation might give better descriptions of the generated THz polarization states. The further investigation has been planned and underway in order to establish connections between the photocurrent model and the four-wave mixing model.

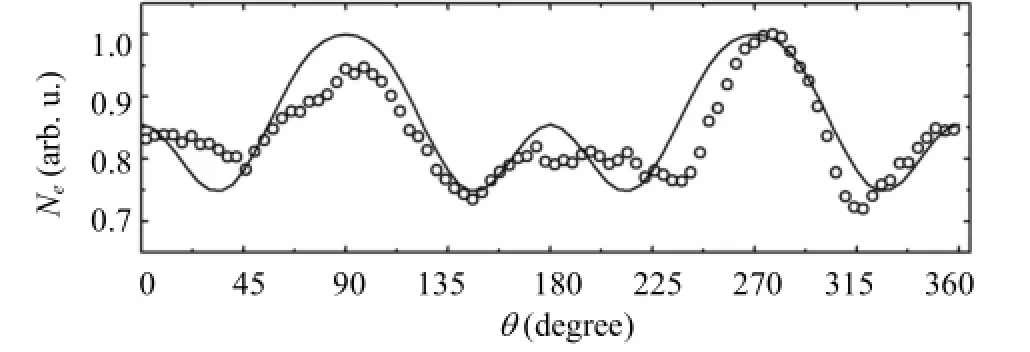
Fig. 5. Variation ofNe(open circles) as a function ofθ. The solid line is simulated according to the static tunneling ionization model.

As for the aforementioned elliptical polarized THz wave, Dietzeet al.[31]and Chenet al.[30]had different ideas about the underlying mechanisms. Dietzeet al.also found that the four-wave mixing model correctly described the measured dependence of THz peak amplitude on relative angle between fundamental and second-harmonic pulses. They considered the four-wave mixing in the neutral air as the dominant process for typical parameters used in two-color THz emission experiments from the plasma filament, rather than the photocurrent model. Nevertheless, Chenet al.attributed the discovered elliptically polarized THz pulse to four-wave optical rectification inside the filament zone where the inversion symmetry of air was broken.

As for the evolution of THz polarization from linear to elliptical achieved with increasing plasma length, Youet al.[33]and Manceauet al.[34]offered different explanations. The former has attributed the polarization evolution to two joint effects occurring on the plasma filament: a successive polarization rotation of local THz plasma sources, caused by laser phase and polarization modulations, and the velocity mismatch between laser and THz, which produced an elliptical THz pulse from a series of time-delayed, polarization rotating local THz fields. On the other hand, Manceauet al.interpreted the variation of the THz polarization to the increasing birefringence induced by the extended filament. As the plasma was getting elongated, the local THz radiation generated along the filament would experience a stronger birefringence, which in turn resulted in an increased THz ellipticity, up to the point where the polarization became fully circular.

3.3 Characterization of Optical Properties (Mainly Birefringence and Nonlinear) of Crystals

With one-dimensional THz-TDS, one can measure the absorption coefficient, refractive index, and dispersion in THz frequency region of various kinds of materials such as crystalline dielectrics and semiconductors[53]. As for the measurement of material absorption coefficient, the observed THz signal decreases after the THz pulse travels through a sample is commonly explained as being caused bymaterial absorption or scattering[42].

However, crystal birefringence can also result in transmission signal minimum, i.e., the so-called fake absorption feature[42], induced by a polarization rotation of the light signal within the detected frequency range. For example, at one certain THz frequency, the phase retardation between two axes of a sample crystal isπ, and at this moment, the crystal acts as a THz half-wave plate. Since a typical characteristic of one-dimensional THz-TDS is that only one component of the THz electric field vector is measured, the observed transmission minimum would be misunderstood as an absorption peak.

For instance, Estacioet al.[54]have attributed the observed transmission spectrum minimum of a 1-mm-thick beta barium borate (BBO) crystal at 0.65 THz to a low-frequency phonon absorption mode. However, in [55], no significant feature below 1 THz in BBO crystal was found, and the authors suggested that the birefringence effect, instead of material absorption, might be responsible for the observed transmission minimum. Fake absorption feature was discovered in a 2-mm-thick quartz crystal by Zhanget al.[42]that the observed absorption peak at 1.57 THz is caused by the birefringence instead of the phonon absorption.

With two-dimensional THz-TDS, due to both orthogonal polarization components of a THz electric field vector can be measured, one can exactly and immediately know if the transmission loss is real or fake absorption feature, by rotating the THz linear polarizer, together with the EO crystal, by 90 degree[42]. If the transmission minimum of the detected THz signal still exists, then it is a real absorption; otherwise, the minimum is caused by the THz polarization rotation induced by birefringence effect in the sample crystal, in which situation the crystal acts as an analogous quarter- or half-wave plate[56].

Another advantage of two-dimensional THz-TDS, when characterizing birefringent material, is no need to have a priori knowledge of the exact crystal orientation[42], compared with previous works[54],[55]. One can tell the optical axis orientation by measuring the azimuthal angle dependence of orthogonal THz transmissions of the sample[42]. Thus, two-dimensional THz-TDS is a significant complement to the traditional optical property characterization of crystals, especially when the measurement of absorption coefficient or birefringent is the central concern, and the exact optical axis orientation of the sample is unknown.

Via two-dimensional THz-TDS, linear optical characteristics of various types of crystals in the THz region have been extensively studied[42],[53]–[59]. For instance, BBO crystal, Estacioet al.[54]and Liuet al.[55]reported the birefringence and refractive index of BBO crystal in the THz region. Their results have also suggested that the absorption coefficients of BBO crystal are lower than those of LiNbO3and LiTaO3at low frequencies, making BBO crystal more attractive for THz applications, such as the optical rectification in BBO crystal to generate the THz wave. Nevertheless, the nonlinear optical properties of BBO crystal in the THz band are rarely known, and there is a lack of knowledge about the nonlinearity tensor which governs the optical rectification process. Hence, Zhanget al.[26]have studied the nonlinearity of BBO crystal via two-dimensional THz-TDS. By measuring the instantaneous electric field of the THz generated through the optical rectification process inside the BBO crystal, Zhanget al. experimentally studied the second order nonlinearity tensor coefficients of BBO crystal in the THz band.

Their experiment setup is similar to that in [27]. A 0.1-mm-thick type-І BBO crystal with a cutting angle a 29.2 degree was inserted in the pumping beam path to produce THz pulse. Especially, a Teflon plate was placed before the geometry focus of the beam to prevent the generation of plasma in air. Thus, the THz signal only came from the BBO crystal. Laboratory coordinate systemXYZand the BBO rotation angleθwere defined exactly the same as in Section 3.1 and Section 3.2. The electric field ofETHz,XandETHz,Ywere obtained for variedθ. By retrieving the instantaneous THz electric field vector withETHz,XandETHz,Y, it is found that the polarization of the THz wave remains linear, and the ordinary THz wave almost vanishes. That is,ETHz,ois absent for all theθ. This observation has resulted in the conclusion thatd22≈0 for BBO crystal in the THz band during the THz generation by optical rectification, sinceETHz,ois proportional tod22according to (5) in Zhang’s work. It is known thatd22is one of the effective optical susceptibilitiesdeffused to investigate the nonlinear susceptibility tensor, andd22generally has the largest value among the nonlinearity tensor coefficients in the visible and near-infrared region.

Then, the peak-to-peak amplitudes ofETHz,X(θ) andETHz,Y(θ) have been retrieved and shown in Fig. 6 (a) as open circles and Fig. 6 (b) as open triangles, respectively. According to (8) in [26], the best fitting of the experimental data can be achieved when a proportional relationship among three independent coefficients, i.e.,d15,d31, andd33, reachd33=-5.6d31-6.5d15, as indicated by the solid lines in Fig. 6. A relative ratio of a number of nonzero nonlinearity tensor coefficients has been empirically revealed for the optical rectification process in BBO crystal which effectively gives a rise to THz generation. This method is also applicable to similar nonlinearity study in THz region of other types of crystals.

3.4 Other Applications

Apart from the applications of two-dimensional THz-TDS mentioned above, there are many other applications, such as inspection of metamaterial-based THz polarization rotator[60],[61], carbon nanotube polarizer[62],[63], circular dichroism of protein[64]–[66], THz Hall effect on semiconductor[9], and THz polarization imaging[38],[67]–[69]. In all situations, orthogonal THz polarization components need to be detected, so that the different sample information encoded in different THz polarizations could be fully achieved. Hence, two-dimensional THz-TDS is undoubtedly an invaluable tool.

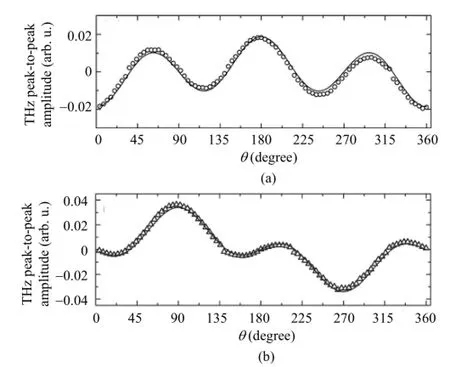
Fig. 6. Variation of THz peak-to-peak amplitude as a function ofθ: (a)ETHz,X(open circles). The solid lines are the corresponding fitting curves according to (8) in [26], and (b) the same as (a) forETHz,Y(open triangles).

4. Conclusions

In this review, the developing progress of two-dimensional THz-TDS over the past few decades has been introduced. One can perform two-dimensional THz-TDS measurement either by a rotation of a THz linear polarizer, or by two separate PCA detectors or EOS systems. For the sake of convenient, the use of a multi-contact PCA receiver or an improved THz-ABCD is another good choice. Then, our central concern lies on the EOS based two-dimensional THz-TDS and its diverse applications, like the analysis of the polarization of THz radiation from a laser-induced plasma source. Radial, linear, elliptical, and circular polarized THz emissions from plasma filaments have all been observed via twodimensional THz-TDS. With total polarization information contained in a THz pulse, the study of the underlying physical mechanism of THz radiation during filamentation has been carried out consequently. We have also presented the characterization of the optical properties of crystals, such as birefringence effect, as well as nonlinear, and briefly introduced other applications of two-dimensional THz-TDS that range from inspection of metamaterial-based THz optical devices to THz polarization imaging.

Acknowledgment

Authors acknowledge the support of the open research funds of State Key Laboratory of High Field Laser Physics, Shanghai Institute of Optics and Fine Mechanics (SIOM).

[1] M. Tonouchi, “Cutting-edge terahertz technology,”Nature Photonics, vol. 1, pp. 97–105, Feb. 2007.

[2] D. H. Auston, K. P. Cheung, and P. R. Smith, “Picosecond photoconducting Hertzian dipoles,”Applied Physics Letters, vol. 45, pp. 284–286, May 1984.

[3] A. Nahata, D. H. Auston, T. F. Heinz, and C. Wu, “Coherent detection of freely propagating terahertz radiation by electro-optic sampling,”Applied Physics Letters, vol. 68, pp. 150–152, Oct. 1996.

[4] P. U. Jepsen, C. Winnewisser, M. Schall, V. Schyja, S. R. Keiding, and H. Helm, “Detection of THz pulses by phase retardation in lithium tantalite,”Physical Review E, vol. 53, pp. R3052, Apr. 1996.

[5] Q. Wu and X.-C. Zhang, “Free-space electro-optic sampling of terahertz beams,”Applied Physics Letters, vol. 67, pp. 3523–3525, Oct. 1995.

[6] C. D’Amico, A. Houard, M. Franco, B. Prade, A. Mysyrowicz, A. Couairon, and V. T. Tikhonchuk, “Conical forward THz emission from femtosecond-laser-beam filamentation in air,”Physical Review Letters, vol. 98, pp. 235002, Jun. 2007.

[7] B. Scherger, N. Born, C. Jansen, S. Schumann, M. Koch, and K. Wiesauer, “Compression molded terahertz transmission blaze-grating,”IEEE Trans. on Terahertz Science and Technology, vol. 2, pp. 556–561, Aug. 2012.

[8] A. Houard, Y. Liu, B. Prade, and A. Mysyrowicz,“Polarization analysis of terahertz radiation generated by four-wave mixing in air,”Optics Letters, vol. 33, pp. 1195–1197, Jun. 2008.

[9] D. M. Mittleman, J. Cunningham, M. C. Nuss, and M. Geva,“Noncontact semiconductor wafer characterization with the terahertz Hall effect,”Applied Physics Letters, vol. 71, pp. 16–18, May 1997.

[10] M. B. Byrne, M. U. Shaukat, J. E. Cunningham, E. H. Linfield, and A. G. Davies, “Simultaneous measurement of orthogonal components of polarization in a free-space propagating terahertz signal using electro-optic detection,”Applied Physics Letters, vol. 98, pp. 151104, Mar. 2011.

[11] E. Castro-Camus, J. Lloyd-Hughes, M. B. Johnston, M. D. Fraser, H. H. Tan, and C. Jagadish, “Polarization-sensitive terahertz detection by multicontact photoconductive receivers,”Applied Physics Letters, vol. 86, pp. 254102, May 2005.

[12] E. Castro-Camus, J. Lloyd-Hughes, L. Fu, H. H. Tan, C. Jagadish, and M. B. Johnston, “An ion-implanted InP receiver for polarization resolved terahertz spectroscopy,”Optics Express, vol. 15, pp. 7047–7057, May 2007.

[13] H. Makabe, Y. Hirota, M. Tani, and M. Hangyo,“Polarization state measurement of terahertz electromagnetic radiation by three-contact photoconductive antenna,”Optics Express, vol. 15, pp. 11650–11657, Sep. 2007.

[14] A. Hussain and S. R. Andrews, “Ultrabroadband polarization analysis of terahertz pulses,”Optics Express, vol. 16, pp. 7251–7257, May 2008.

[15] M. Tani, Y. Hirota, C. T. Que,et al., “Novel terahertz photoconductive antennas,”Int. Journal of Infrared and Millimeter Waves, vol. 27, pp. 531–546, Apr. 2006.

[16] Z. Lü, D. Zhang, C. Meng, L. Sun, Z. Zhou, Z. Zhao, and J. Yuan, “Polarization-sensitive air-biased-coherent-detection for terahertz wave,”Applied Physics Letters, vol. 101, pp.081119, Aug. 2012.

[17] T. Nagashima, M. Tani, and M. Hangyo,“Polarization-sensitive THz-TDS and its application to anisotropy sensing,”Journal of Infrared, Millimeter, and Terahertz Waves, vol. 34, pp. 740–775, Nov. 2013.

[18] W. Xiong and J. Shen, “Fingerprint extraction from interference destruction terahertz spectrum,”Optics Express, vol. 18, pp. 21798–21803, Oct. 2010.

[19] E. Castro-Camus, “Polarization-resolved terahertz time-domain spectroscopy,”Journal of Infrared, Millimeter, and Terahertz Waves, vol. 33, pp. 418–430, Apr. 2012.

[20] C. A. Schmuttenmaer, “Exploring dynamics in the far-infrared with terahertz spectroscopy,”Chemical Reviews, vol. 104, pp. 1759–1780, Mar. 2004.

[21] M. C. Beard, G. M. Turner, and C. A. Schmuttenmaer,“Transient photoconductivity in GaAs as measured by time-resolved terahertz spectroscopy,”Physical Review B, vol. 62, pp. 15764, Dec. 2000.

[22] K. Reimann, R. P. Smith, A. M. Weiner, T. Elsaesser, and M. Woerner, “Direct field-resolved detection of terahertz transients with amplitudes of megavolts per centimeter,”Optics Letters, vol. 28, pp. 471–473, Mar. 2003.

[23] S. G. Park, M. R. Melloch, and A. M. Weiner, “Comparison of terahertz waveforms measured by electro-optic and photoconductive sampling,”Applied Physics Letters, vol. 73, pp. 3184–3186, Sep. 1998.

[24] S. G. Park, M. R. Melloch, and A. M. Weiner, “Analysis of terahertz waveforms measured by photoconductive and electrooptic sampling,”IEEE Journal of Quantum Electronics, vol. 35, pp. 810–819, May 1999.

[25] S. Kono, M. Tani, and K. Sakai, “Ultrabroadband photoconductive detection: Comparison with free-space electro-optic sampling,”Applied Physics Letters, vol. 79, pp. 898–900, Jun. 2001.

[26] Y. Zhang, Y. Zheng, S. Xu, and W. Liu, “Empirical study of nonlinearity tensor dominating THz generation in barium borate crystal through optical rectification,”Applied Physics B, vol. 103, pp. 831–835, Jun. 2011.

[27] Y. Zhang, Y. Chen, S. Xu,et al., “Portraying polarization state of terahertz pulse generated by a two-color laser field in air,”Optics Letters, vol. 34, pp. 2841–2843, Sep. 2009.

[28] N. Yasumatsu and S. Watanabe, “Precise real-time polarization measurement of terahertz electromagnetic waves by a spinning electro-optic sensor,”Review of ScientificInstruments, vol. 83, pp. 023104, Jan. 2012.

[29] S. Watanabe, N. Yasumatsu, K. Oguchi, M. Takeda, T. Suzuki, and T. Tachizaki, “A real-time terahertz time-domain polarization analyzer with 80-MHz repetition-rate femtosecond laser pulses,”Sensors, vol. 13, pp. 3299–3312, Mar. 2013.

[30] Y. Chen, C. Marceau, S. Génier, F. Théberge, M. Châteauneuf, J. Dubois, and S. L. Chin, “Elliptically polarized terahertz emission through four-wave mixing in a two-color filament in air,”Optics Communications, vol. 282, pp. 4283–4287, Nov. 2009.

[31] D. Dietze, J. Darmo, S. Roither, A. Pugzlys, J. N. Heyman, and K. Unterrainer, “Polarization of terahertz radiation from laser generated plasma filaments,”JOSA B, vol. 26, pp. 2016–2027, Nov. 2009.

[32] P. Planken, H. K. Nienhuys, H. J. Bakker, and T. Wenckebach, “Measurement and calculation of the orientation dependence of terahertz pulse detection in ZnTe,”JOSA B, vol. 18, pp. 313–317, Mar. 2001.

[33] Y. S. You, T. I. Oh, and K. Y. Kim, “Mechanism of elliptically polarized terahertz generation in two-color laser filamentation,”Optics Letters, vol. 38, pp. 1034–1036, Apr. 2013.

[34] J. M. Manceau, M. Massaouti, and S. Tzortzakis, “Coherent control of THz pulses polarization from femtosecond laser filaments in gases,”Optics Express, vol. 18, pp. 18894–18899, Aug. 2010.

[35] Q. Chen, M. Tani, Z. Jiang, and X.-C. Zhang, “Electro-optic transceivers for terahertz-wave applications,”JOSA B, vol. 18, pp. 823–831, Jun. 2001.

[36] N. C. J. van der Valk, T. Wenckebach, and P. Planken, “Full mathematical description of electro-optic detection in optically isotropic crystals,”JOSA B, vol. 21, pp. 622–631, Mar. 2004.

[37] A. J. Adam, J. M. Brok, P. C. Planken, M. A. Seo, and D. S. Kim, “THz near-field measurements of metal structures,”Comptes Rendus Physique, vol. 9, pp. 161–168, Mar. 2008.

[38] R. Zhang, Y. Cui, W. Sun, and Y. Zhang, “Polarization information for terahertz imaging,”Applied Optics, vol. 47, pp. 6422–6427, Dec. 2008.

[39] L. Zhang, H. Zhong, C. Deng, C. Zhang, and Y. Zhao,“Terahertz polarization imaging with birefringent materials,”Optics Communications, vol. 283, pp. 4993–4995, Dec. 2010.

[40] K. Wiesauer and C. Jördens, “Recent advances in birefringence studies at THz frequencies,”Journal of Infrared, Millimeter, and Terahertz Waves, vol. 34, pp. 663–681, Nov. 2013.

[41] J. N. Heyman, D. Bell, and T. Khumalo, “Terahertz photo-Hall measurements of carrier mobility in GaAs and InP,”Applied Physics Letters, vol. 88, pp. 162104, Jan. 2006.

[42] L. Zhang, H. Zhong, C. Deng, C. Zhang, and Y. Zhao,“Polarization sensitive terahertz time-domain spectroscopy for birefringent materials,”Applied Physics Letters, vol. 94, pp. 211106, May 2009.

[43] Y. Zhang, Y. Chen, C. Marceau,et al., “Non-radially polarized THz pulse emitted from femtosecond laser filament in air,”Optics Express, vol. 16, pp. 15483–15488, Sep. 2008.

[44] Y. Chen, C. Marceau, W. Liu,et al., “Elliptically polarized terahertz emission in the forward direction of a femtosecond laser filament in air,”Applied Physics Letters, vol. 93, pp. 231116, Nov. 2008.

[45] Y. Ikebe, T. Morimoto, R. Masutomi, T. Okamoto, H. Aoki, and R. Shimano, “Optical Hall effect in the integer quantum Hall regime,”Physical review letters, vol. 104, pp. 256802, Jun. 2010.

[46] K. Kozuki, T. Nagashima, and M. Hangyo, “Measurement of electron paramagnetic resonance using terahertztime-domain spectroscopy,”Optics Express, vol. 19, pp. 24950–24956, Dec. 2011.

[47] K. Y. Kim, J. H. Glownia, A. J. Taylor, and G. Rodriguez,“Terahertz emission from ultrafast ionizing air in symmetry-broken laser fields,”Optics Express, vol. 15, pp. 4577–4584, Apr. 2007.

[48] S. Xu, Y. Zhang, Y. Zheng, and W. Liu, “Study of physical mechanism of two-color laser field pumped THz wave in air plasma,”Terahertz Science and Technology, vol. 3, pp. 130, Sep. 2010.

[49] S. Xu, Y. Zhang, W. Liu, and S. L. Chin, “Experimental confirmation of high-stability of fluorescence in a femtosecond laser filament in air,”Optics Communications, vol. 282, pp. 4800–4804, Dec. 2009.

[50] H. G. Roskos, M. D. Thomson, M. Kreß, and T. Löffler,“Broadband THz emission from gas plasmas induced by femtosecond optical pulses: From fundamentals to applications,”Laser & Photonics Reviews, vol. 1, pp. 349–368, Nov. 2007.

[51] J. Zhao, Y. Zhang, Z. Wang,et al., “Propagation of terahertz wave inside femtosecond laser filament in air,”Laser Physics Letters, vol. 11, pp. 095302, Jul. 2014.

[52] J. Zhao, W. Chu, L. Guo,et al.“Terahertz imaging with sub-wavelength resolution by femtosecond laser filament in air,”Scientific Reports, vol. 4, pp. 3880, Jan. 2014.

[53] D. Grischkowsky, S. Keiding, M. V. Exter, and C. Fattinger,“Far-infrared time-domain spectroscopy with terahertz beams of dielectrics and semiconductors,”JOSA B, vol. 7, pp. 2006–2015, Oct. 1990.

[54] E. Estacio, S. Saito, T. Nakazato,et al., “Birefringence of β-BaB2O4 crystal in the terahertz region for parametric device design,”Applied Physics Letters, vol. 92, pp. 091116, Feb. 2008.

[55] J. Liu, X. Guo, J. Dai, and X.-C. Zhang, “Optical property of beta barium borate in terahertz region,”Applied Physics Letters, vol. 93, pp. 171102, Oct. 2008.

[56] J. Lloyd-Hughes, S. P. P. Jones, E. Castro-Camus, K. I. Doig, and J. L. MacManus-Driscoll, “Modifying the polarization state of terahertz radiation using anisotropic twin-domains in LaAlO3,”Optics Letters, vol. 39, pp. 1121–1124, Mar. 2014.

[57] L. Zhang, H. Zhong, C. Deng, C. Zhang, and Y. Zhao,“Characterization of birefringent material using polarization-controlled terahertz spectroscopy,”Optics Express, vol. 18, pp. 20491–20497, Sep. 2010.

[58] C. Jördens, M. Scheller, M. Wichmann, M. Mikulics, K. Wiesauer, and M. Koch, “Terahertz birefringence for orientation analysis,”Applied Optics, vol. 48, pp. 2037–2044, Apr. 2009.

[59] M. Pfleger, H. Roitner, H. Pühringer, K. Wiesauer, H. Grün, and S. Katletz, “Advanced birefringence measurements in standard terahertz time-domain spectroscopy,”AppliedOptics, vol. 53, pp. 3183–3190, May 2014.

[60] L. Cong, W. Cao, X. Zhang,et al., “A perfect metamaterial polarization rotator,”Applied Physics Letters, vol. 103, pp. 171107, Oct. 2013.

[61] X. Wen and J. Zheng, “Broadband THz reflective polarization rotator by multiple plasmon resonances,”Optics Express, vol. 22, pp. 28292–28300, Nov. 2014.

[62] L. Ren, C. L. Pint, L. G. Booshehri,et al., “Carbon nanotube terahertz polarizer,”Nano Letters, vol. 9, pp. 2610–2613, Jun. 2009.

[63] X. L. Xu, P. Parkinson, K. C. Chuang, M. B. Johnston, R. J. Nicholas, and L. M. Herz, “Dynamic terahertz polarization in single-walled carbon nanotubes,”Physical Review B, vol. 82, pp. 085441, Aug. 2010.

[64] E. Castro-Camus and M. B. Johnston, “Conformational changes of photoactive yellow protein monitored by terahertz spectroscopy,”Chemical Physics Letters, vol. 455, pp. 289–292, Apr. 2008.

[65] J. Xu, G. J. Ramian, J. F. Galan,et al.“Terahertz circular dichroism spectroscopy: A potential approach to the in situ detection of life’s metabolic and genetic machinery,”Astrobiology, vol. 3, pp. 489–504, Jul. 2003.

[66] J. Xu, J. Galan, G. Ramian,et al., “Terahertz circular dichroism spectroscopy of biomolecules,”Optical Technologies for Industrial, Environmental, and Biological Sensing. Int. Society for Optics and Photonics, 2004, pp. 19–26.

[67] N. C. J. Van der Valk, W. A. M. van der Marel, and P. Planken, “Terahertz polarization imaging,”Optics Letters, vol. 30, pp. 2802–2804, Oct. 2005.

[68] N. Yasumatsu and S. Watanabe, “T-ray topography by time-domain polarimetry,”Optics Letters, vol. 37, pp. 2706–2708, Jul. 2012.

[69] S. Katletz, M. Pfleger, and H. Pühringer,et al., “Polarization sensitive terahertz imaging: Detection of birefringence and optical axis,”Optics Express, vol. 20, pp. 23025–23035, Oct. 2012.

Jia-Yu Zhao was born in Liaoning, China in 1988. He received the B.S. degree from Nankai University, Tianjin in 2011. He is currently pursuing the Ph.D. degree with Nankai University. His research interests include terahertz optoelectronics and spectroscopy.

Wei-Wei Liu was born in 1976 in Huai’an, China. He received his Ph.D. degree from Laval University, Canada. Currently, he is a professor with the Institute of Modern Optics of Nankai University. His recent research interests focus on THz science and technology.

Manuscript received February 1, 2015; revised March 10, 2015. This work was supported by the National Basic Research Program of China under Grant No. 2014CB339802, No. 2011CB808100, and the National Natural Science Foundation of China under Grant No. 11174156.

J.-Y. Zhao is with the Key Laboratory of Optical Information Science and Technology of Ministry of Education, Nankai University, Tianjin 300071, China (e-mail: zhaojiayu@mail.nankai.edu.cn).

W.-W. Liu is with the Key Laboratory of Optical Information Science and Technology of Ministry of Education, Nankai University, Tianjin 300071, China (Corresponding author e-mail: liuweiwei@nankai.edu.cn).

Color versions of one or more of the figures in this paper are available online at http://www.journal.uestc.edu.cn.

Digital Object Identifier: 10.3969/j.issn.1674-862X.2015.01.003