Pairing-Free ID-Based Key-Insulated Signature Scheme

Guo-Bin Zhu, Hu Xiong, and Zhi-Guang Qin

Pairing-Free ID-Based Key-Insulated Signature Scheme

Guo-Bin Zhu, Hu Xiong, and Zhi-Guang Qin

—Without the assumption that the private keys are kept secure perfectly, cryptographic primitives cannot be deployed in the insecure environments where the key leakage is inevitable. In order to reduce the damage caused by the key exposure in the identity-based (ID-based) signature scenarios efficiently, we propose an ID-based key-insulated signature scheme in this paper, which eliminates the expensive bilinear pairing operations. Compared with the previous work, our scheme minimizes the computation cost without any extra cost. Under the discrete logarithm (DL) assumption, a security proof of our scheme in the random oracle model has also been given.

Index Terms—Identity-based cryptography, keyinsulated, random oracle mode, signature.

1. Introduction

As more and more cryptographic primitives have been applied in insecure environments, the key-evolving protocols in the public key setting, such as the key-insulated[1],[2], intrusion-resilience[3],[4], and forward secure[5],[6]cryptosystems, have been put forward independently to deal with the key exposure problem. It is the basic idea behind the key-evolving method that the secret key will be evolved over time, while the corresponding public key remains unaltered during the lifetime of the private key. In this manner, the exposure of the secret keys in a given time period will not affect the secret keys in other time periods. As one of the key-evolution mechanisms, the key-insulated cryptosystem[1],[2]achieves key exposure resilience by dividing the secret key of the user into two parts: a temporary secret key held by the user and a helper key keptby a physically-secure but computationally-limited “helper”. The temporary secret key will be refreshed in each time period with the support from the helper, instead of the public key corresponding to this secret key remaining fixed over the whole lifetime of this private key. Since then, many schemes in this area have been presented including many key-insulated signature schemes[7]-[11].

However, when the key-insulated signature is deployed in the public key infrastructure (PKI), a certificate should be issued by a certificate authority (CA) to establish the connection between the public key of the user and its corresponding identity. Before the signature is verified, the validity of this identity certificate should be guaranteed. Usually, the cost of maintaining, transferring, and validating the certificate is considered to be expensive. To reduce the overhead and complexity of the certificate management in traditional PKI, Shamir introduced the identity-based public key cryptography (ID-PKC)[12]. In ID-PKC environments, the public key of the user can be easily gained from his known identity information such as the email address or the telephone number. Meanwhile, a fully-trusted private key generator (PKG) is involved to generate the private key. In this case, the certificates in the conventional PKI can be eliminated in the ID-PKC. Observing the benefits of the key-insulated signature and ID-PKC, Zhouet al.[13]formalized the notion of the ID-based key-insulated signature (ID-KIS) scheme and proposed the first concrete construction from bilinear pairings. To afford a strong key-insulated property, Wenget al.[14]re-formalized the definition and security models of the ID-KIS scheme, and proposed a novel scheme along with the secure key-update. Taking different scenarios into account, extensions of the ID-KIS scheme, such as the ID-based parallel key-insulated signature[15],[16], ID-based key-insulated signcryption[17], ID-based key-insulated ring signature[18], ID-based key-insulated proxy signature[19], and ID-based key-insulated signature with batch verification[20], have also been investigated. Nevertheless, all of the existing ID-KIS schemes are constructed based on the bilinear pairings. Although the computation of the pairing is speeding up significantly, the pairing is still considered as the most expensive cryptographic operations so far[21]. Therefore, constructing an efficient and provably-secure ID-KIS scheme without pairing is an interesting and inspiring problem.

In this paper, we propose an efficient and simpleID-KIS scheme and show its security in the random oracle model with the assumption that the DL problem is intractable. Compared with the previous ID-KIS schemes, our scheme is very efficient in terms of computation cost since the expensive bilinear pairing operation is eliminated from our scheme. To the best of authors’ knowledge, this is the first pairing-free ID-KIS scheme in literature.

The rest of this paper is organized as follows. The mathematical background and the security model of ID-KIS scheme are given in Section 2. The concrete construction of the proposed scheme and the security proof is followed in Section 3 and Section 4, respectively. Finally, a concise conclusion is presented in Section 5.

2. Preliminaries

In this section, we will review some fundamental backgrounds such as the mathematical assumption, and the formal definition and security models of the ID-KIS scheme.

2.1 Mathematical Assumption

Definition 2.1[DL Assumption] On input a group G of prime orderqwith a generatorgand elementfor a random value, the DL problem consists of computing the elementx, whereis finite field with orderq.

The success probability of an algorithmAin solving the DL problem in G is defined as=Pr[A(g,gx)=x∈] and the DL assumption refers thatis negligible.

2.2 Security Notions

A. Syntax of ID-KIS Scheme

An ID-KIS scheme ID-KIS=(Setup, Extract, Update*, Update, Sign, Verify) is specified by the following six polynomial-time algorithms:

1) Setup: On inputting a security parameterk, this randomized algorithm, which is usually performed by the trusted PKG, outputs the master public/secret key pair (mpk, psk) along with the total number of time periodsN. The PKG publishes the public parameters (mpk,N) and keeps the master secret key msk secretly by itself.

2) Extract: On inputting user’s identity ID, this randomized algorithm, which is also executed by the PKG, generates the initial private key TSKID,0and the helper key HKID. TSKID,0is sent securely to the corresponding user, and HKIDis stored in a physically-secure but computationally-limited device named “helper”.

3) Update*: On inputting user’s identity ID, the helper key HKID, and the time period indicesiandj, this randomized algorithm, which is run by the helper held by the corresponding user, generates the partial secret key PSKID,i,j.

4) Update: On inputting the temporary secret key TSKID,jfor the time periodj, and the partial secret key PSKID,i,jfor time period indicesiandj, this randomized algorithm, which is run by the user itself, generates the temporary secret key TSKID,ifor the time periodi.

5) Sign: On inputting a temporary secret key TSKID,ifor the time periodi, and a messagem, this randomized algorithm outputs a signature (σ,i) ← Sign(TSKID,i,m,i), where ← means generating signature.

6) Verify: On inputting the master public key mpk, user identity ID, a time periodi, and corresponding signatureσ, this randomized algorithm outputs True if the signature is correct, or ⊥ otherwise.

The consistency of ID-KIS scheme requires that for∀i∈ {1 ,2,… ,N} ,ID ∈{0,1}*, ∀m∈M, Verify((σ,i),m, ID)=True always holds, where {}*⋅ is the string with arbitrary length, and (σ,i) ← Sign(TSKID,i,m,i) andMdenote the message space.

B. Adversaries Model of ID-KIS Scheme

We review the security model of ID-KIS scheme in the follows. The oracles, which can be accessed by the adversaryA, are depicted as follows.

a) Initial key extract query: Given an identity ID, this initial secret key oracle outputs the initial private key TSKID,0and helper key HKIDif this identity has not been queried yet; otherwise, nothing is to be carried out. Then the item (ID, TSKID,0, HKID) is stored into a listL.

b) Helper key extract query: Given an identity ID, this helper key extract oracle executes the extract algorithm to generate the helper key HKID.

c) Temporary secret key extract query: Given an identity ID along with the time periodi, this temporary secret key oracle executes the update algorithm to output the temporary secret key TSKID,i.

d) Signing query: Given a messagemfor ID in the time periodi, this signing oracle outputs a valid signatureσsuch that True ←Verify( m pk,ID,i,σ).

We define two games, one for formalizing the perfect key-insulated property and the other one for simulating the strong key-insulated property. Note that the adoption of helper key extract queries or initial key extract queries can be considered as the difference between these two games.

Game 1: LetSbe the challenger with the input of security parameterk.

·Sexecutes Setup(k) to get (mpk, msk).

·SrunsAonkand mpk. During the simulation,Acan make queries adaptively onto the initial key extract query, temporary secret key extract query, and signing query oracles.

·Ais to output a tuple (σ*,i*) for messagem*on identity ID*. We say thatAwins Game 1 if the followingconditions are satisfied:

1) True ←Verify((σ*,i*),m*,ID*);

2)Ais disallowed to issue an initial key extract query on identity ID*;

3) (ID*,i*) has not been submitted to the temporary secret key extract query;

4) The oracle signing query has never queried with (i*,m*, ID*).

Definition 2.2An ID-KIS scheme is said to be perfectly key-insulated if there is no probabilistic polynomial-time adversaryAwho wins Game 1 with non-negligible advantages.

Game 2: LetSbe the challenger with the input of security parameterk.

·Sexecutes Setup(k) to get (mpk, msk).

·SrunsAonkand mpk. During the simulation,Acan make queries adaptively onto the initial key extract query, helper key extract query, and signing query oracles.

·Ais to output a tuple (σ*,i*) for messagem*on identity ID*. We say thatAwins Game 2 if the following conditions are satisfied:

1) True ←Verify((σ*,i*),m*,ID*);

2)Ais disallowed to issue an initial key extract query on identity ID*;

3) The oracle signing query has never queried with (i*,m*, ID*).

Definition 2.3An ID-KIS scheme is said to be strong key-insulated if there is no probabilistic polynomial-time adversaryAwho wins Game 2 with non-negligible advantages.

In fact, the attacker who can compromise the helper device is captured in Game 2. During this game, the helper key for the target identity ID*can be extracted by the adversary, while only the temporary secret key can be derived by the adversary in Game 1.

3. Proposed Scheme

The concrete construction of the proposed ID-KIS scheme without pairing based on [22] is given in this section, which comprises the following parts.

Setup: Given a security parameterk, the algorithm works as follows:

1) Run the parameter generator on the inputkto generate a prime orderq, a multiplicative group G of prime orderq, and a generatorg∈G.

3) For, compute, where

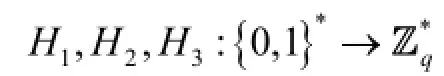
Extract: Given a user’s identity { }*ID∈0,1 , PKG generates the initial private key and the helper key as follows:

3) Return the initial secret key (R,TSKID,0) to the user ID secretly and store the helper key (HKID,R) in the helper.

Update*: The helper generates the partial temporary secret key PSKID,i,jfor the user ID and time period indicesiandjas follows:

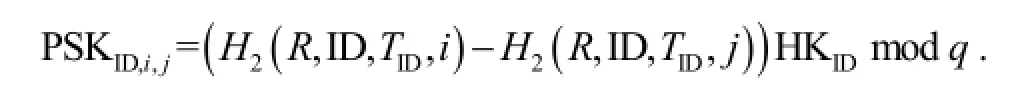
Update: Given the partial temporary secret key PSKID,i,jand the temporary secret key (R,TSKID,j) =(R,SID,j,TID) for a time periodj, the user associated with the identity ID computes his temporary secret key for time periodias TSKID,i=(R,SID,i,TID), whereSID,i=SID,j+ PSKID,i,j.

4) Output (Y,R,z,TID) as the signature onmin time periodi.

Verify: To verify a signature (Y,R,z,TID) signed by user ID on messagesm, the verifier performs the following steps:

1) Computeh=H3(i,Y,R,m).

2) Check whether the following equation:

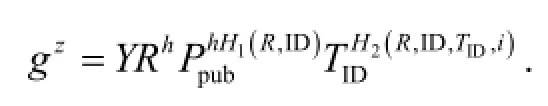
holds or not. If it holds, accept the signature; else reject it.

And the correctness of our scheme can be described as

4. Analysis of Proposed Scheme

4.1 Security Proof

Assuming that the DL problem is hard, we now show the security of our ID-KIS scheme as follows.

Theorem 4.1In the random oracle model, our ID-KIS scheme is perfectly key-insulated under the assumption that the DL problem in G is intractable. If a probabilistic polynomial-time forger Λ has forged a signature in an attack modeled by Game 1 of Definition 2.2, then the DL problem can be solved.

Proof. Letbe a random instance of the DL problem in G, wheregis a generator of G with the prime orderq, and the elementαis taken uniformly at random in. By using the forgery algorithm Λ, we will construct an algorithmSwhich outputs the DL solutionαin

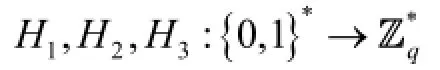
H1-queries: To respond toH1-queries, algorithmSmaintains a table of tuples (R,ID,h1) explained below, whereh1is randomly chosen from. We refer to this table as the TABH1. This table is initially empty. When Λ queries the oracleH1at a point (R,ID), algorithmSresponds as follows:

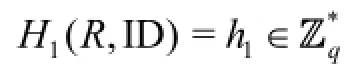
2) Otherwise,Spicks a randomh1∈G1, adds the tuple (R, ID,h1) to the TABH1, and responds withH1(R,ID) =h1as the answer.

H2-queries: To respond toH2-queries, algorithmSmaintains a table of tuples (R, ID,TID,i,h2), whereh2is chosen randomly from. We refer to this table as the TABH2. This table is initially empty. When Λ queries the oracleH2at a point (v, ID,i), algorithmSresponds as follows:

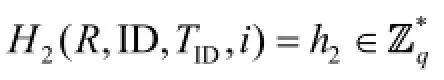
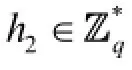
H3-queries: To respond toH3-queries, algorithmSmaintains a table of tuples (i,Y,R,m,h3) explained below, which is named as the TABH3. This table is initially empty. When Λ queries the oracleH3at a point (i,Y,R,m), algorithmSresponds as follows:

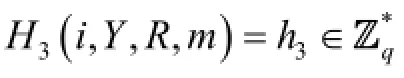
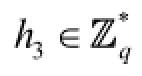
Initial key extract queries: Every time Λ asks for the initial secret key corresponding to an identity ID,Smaintains a table TABSKof tuples (ID,R,SID,0,TID,hkID,i), which is initially empty, and simulates the oracle as follows.

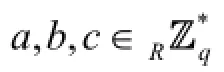
Temporary secret key queries: When Λ queries a temporary secret key with identity ID and time periodi, algorithmSresponds as follows:

1) If the query (i,ID) has already appeared in a tuple (ID,R,SID,0,TID,hkID,i) of TABSK, then algorithmSresponds (R,SID,0,TID) as the answer.

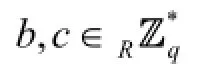
Signing queries: Regarding to the signing queries, the attacker Λ can ask for a valid signature on the messagem∈ {0 ,1}*, the identity ID, and the time periodi. If the item (i,ID) has already appeared in a tuple (ID,R,SID,0,TID,hkID,i) of TABSK, thenSsigns this message using this temporary secret key according to the sign algorithm depicted in Section 3. It outputs the signature (Y,R,z,TID) for the message and stores the value (i,Y,R,m,h3) in table TABH3, whereh3=H3(i,Y,R,m)to keep consistency. If the item (i,ID) has not been queried to temporary secret key oracles,Sperforms the simulation of the temporary secret key oracle and signs the message using the returning secret key.

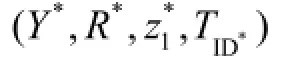
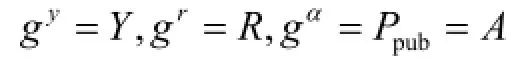
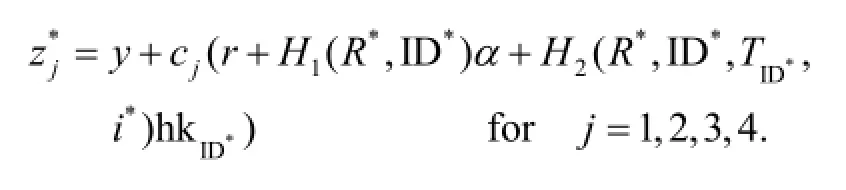
The algorithmScan solve the values ofy,r,α, andfrom the above four independent linear equations since onlyy,r,α,are unknown in these equations. Therefore, we can find a solution of the DL problem by outputtingα.

Theorem 4.2.In the random oracle model, our ID-KIS scheme is strong key-insulated under the assumption that the DL problem in G is intractable. If a probabilistic polynomial-time forger Λ has forged a signature in an attack modeled by Game 2 of Definition 2.3, then the DL problem can be solved.

The proof is similar to those of Theorem 4.1 and is omitted here.

Theorem 4.3.The proposed ID-KIS scheme has secure key updates.

This theorem follows from the fact that for any target identity ID and the corresponding time periodsiandj, only the partial temporary secret key PSKID,i,jalong with the temporary secret keys TSKID,iand TSKID,iwill be revealed.

4.2 Performance Analysis

We compare our scheme with the existing ID-KIS schemes[13],[14]in terms of the signature size and computation cost. According to [22], the exponentiation and multiplication are equivalent to point multiplication and point addition in elliptic curve cryptography (ECC), respectively. Thus, our ID-KIS scheme can be implemented by using ECC with. In view of the computational overhead, we only consider the costly operations and we omit the computation efforts which can be pre-computed. Par denotes a pairing operation, SM a scalar multiplications in G1(exponentiation in G), andEan exponential operation in G2(multiplication in G). The pairing computation Par is more time-consuming than multiplication and exponentiation computation, but Par is eliminated in our scheme. Thus, our scheme is more efficient than the existing schemes according to Table 1.

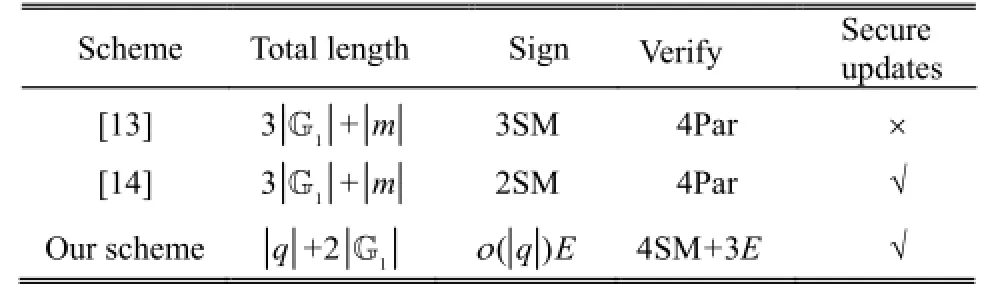
Table 1: Comparison between our scheme and related work

5. Conclusions

In this paper, we have proposed an efficient ID-KIS scheme that does not require any pairing operation in both signing and verification procedures. The scheme offers both perfect key-insulated and strong key-insulated properties. We also prove the security of our scheme under the DL assumption. Compared with previous schemes, our scheme minimizes the computation cost with no extra cost, which favors this scheme’s practical application.

[1] Y. Dodis, J. Katz, S. Xu, and M. Yung, “Key-insulated public key cryptosystems,” inPorc. ofInt. Conf. on the Theory and Applications of Cryptographic Techniques, Amsterdam, 2002, pp. 65-82.

[2] Y. Dodis, J. Katz J, S. Xu, and M. Yung, “Strong key-insulated signature schemes,” inProc. of the 6th Int. Workshop on Practice and Theory in Public Key Cryptography, Miami, 2002, pp. 130-144.

[3] G. Itkis. “Intrusion-resilient signatures: generic constructions,or defeating strong adversary with minimal assumptions,” inProc. of the 3rd Int. Conf. on Security in Communication Networks, Amalfi, 2003, pp. 102-118.

[4] J. Yu, F. Kong, X. Cheng, R. Hao, and J. Fan,“Intrusion-resilient identity-based signature: Security definition and construction,”Journal of Systems and Software, vol. 85, no. 2, pp. 382-391, 2012.

[5] R. Canetti, S. Halevi, and J. Katz. “ A forward-secure public-key encryption scheme,” inProc. of Int. Conf. on the Theory and Applications of Cryptographic Techniques, Warsaw, 2003, pp. 255-271.

[6] G. Itkis and L. Reyzin, “Forward-secure signatures with optimal signing and verifying,” inProc. of Int. Conf. on the Theory and Applications of Cryptographic Techniques, Santa Barbara, 2001, pp. 332-354.

[7] N. González-Deleito, O. Markowitch, and E. Dall’Olio, “A new key-insulated signature scheme,” inProc. of the 6th Int. Conf. on Information and Communications Security, Malaga, 2004, pp. 465-479.

[8] Z. Le, Y. Ouyang, J. Ford, and F. Makedon, “A hierarchical key-insulated signature scheme in the CA trust model,” inProc. of the 7th Int. Conf. on Information Security, Palo Alto, 2004, pp. 280-291.

[9] Y. Lee, J. Ahn, S. Kim, and D. Won, “A PKI system for detecting the exposure of a user’s secret key,” inProc. of the 3rd European PKI Workshop: Theory and Practice, Turin, 2006, pp. 248-250.

[10] G. Ohtake, G. Hanaoka, and K. Ogawa, “An efficient strong key-insulated signature scheme and its application,” inProc. of the 5th European PKI Workshop: Theory and Practice, Trondheim, 2008, pp. 150-165.

[11] D. H. Yum and P. J. Lee, “Efficient key updating signature schemes based on IBS,”Lecture Notes in Computer Sciencevol. 2898, pp. 167-182, 2003, doi: 10.1007/978-3-540-40974-8_14.

[12] A. Shamir, “Identity-based cryptosystems and signature schemes,” inProc. of Int. Conf. on the Theory and Applications of Cryptographic Techniques, Santa Barbara, 1985, pp. 47-53.

[13] Y. Zhou, Z. Cao, and Z. Chai, “Identity based key insulated signature,” inProc. of the 2nd Int. Conf. on Information Security Practice and Experience, Hangzhou, 2006, pp. 226-234.

[14] J. Weng, S. Liu, K. Chen, and X. Li, “Identity-based key-insulated signature with secure key-updates,” inProc. of the 2nd SKLOIS Conf. on Information Security and Cryptology, Beijing, 2006, pp. 13-26.

[15] J. Weng, X. Li, K. Chen, and S. Liu, “Identity-based parallel key-insulated signature without random oracles,”Journal of Information Science and Engineering, vol. 24, no. 4, pp. 1143-1157, 2008.

[16] J. Weng, S. Liu, K. Chen, and X. Li, “Identity-based parallel key-insulated signature: framework and construction,”Journal of Research and Practice in Information Technology, vol. 40, no. 1, pp. 55-68, 2008.

[17] J. Chen, K. Chen, Y. Wang, X. Li, Y. Long, and Z. Wan,“Identity-based key-insulated signcryption,”Informatica, vol. 23, no. 1, pp. 27-45, 2012.

[18] H. Wang and Y. Zhang, “Identity-based strong key-insulated ring signature scheme in the standard model,” inProc. of the 7th Int. Conf. on Mobile Ad-hoc and Sensor Networks, Beijing, 2011, pp. 451-455.

[19] Z. Wan, X. Lai, J. Weng, and Y. Wang, “Identity-based key-insulated proxy signature,”Journal of Electronics (China), vol. 26, no. 6, pp. 853-858, 2009.

[20] T. Y. Wu, Y. M. Tseng, and C. W. Yu. “ID-based key-insulated signature scheme with batch verification and its novel application,”Int. Journal of Innovative Computing, Information and Control, vol. 8, no. 7, pp. 4797-4810, 2012.

[21] L. Chen, Z. Cheng, and N. P. Smart. “Identity-based key agreement protocols from pairings,”Int. Journal of Information Security, vol. 6, no. 4, pp. 213-241, 2007.

[22] J. K. Liu, J. Baek, J. Zhou, Y. Yang, and J. W. Wong,“Efficient online/offline identity-based signature for wireless sensor network,”Int. Journal of Information Security, vol. 9, no. 4, pp. 287-296, 2010.

[23] D. Pointcheval and J. Stern. “Security arguments for digital signatures and blind signatures,”Journal of Cryptology, vol. 13, no. 3, pp. 361-396, 2000.

Guo-Bin Zhu was born in Shanxi, China in 1981. He received his B.S. and M.S. degrees from the University of Electronic Science and Technology of China (UESTC), Chengdu in 2002 and 2008, respectively. He is pursuing his Ph.D. degree with the School of Computer Science and Engineering, UESTC. His research interests include network security and cryptography.

Hu Xiong was born in Guizhou, China in 1982. He received the Ph.D. degree from UESTC, Chengdu in 2009 in information and communication engineering. He is currently an associate professor with the School of Computer Science and Engineering, UESTC. His research interests include network security and cryptography.

Zhi-Guang Qin was born in Sichuan, China in 1956. He received the Ph.D. degree from UESTC, Chengdu in 1996. He works as a full professor with the School of Computer Science and Engineering and the Dean of the School of Computer Science and Engineering, UESTC. His research interests include information security and wireless networks.

Manuscript received February 23, 2014; revised April 12, 2014. This work was supported by the National Natural Science Foundation of China under Grant No. 61003230, No. 61370026, No. 61103206, and No. 61300191, and Chongqing Key Lab of Computer Network and Communication Technology under Grant No. CY-CNCL-2012-02.

G.-B. Zhu is with the School of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu 610054, China (Corresponding author e-mail: zhugb@uestc.edu.cn).

H. Xiong and Z.-G Qin are with the School of Computer Science and Engineering, University of Electronic Science and Technology of China, Chengdu 610054, China (e-mail: xionghu.uestc@gmail.com; qinzg@uestc.edu.cn).

Digital Object Identifier: 10.3969/j.issn.1674-862X.2015.01.007