基于Mallat变换的时间序列模型在短期风速预测中的应用

王维志，陈海毅

(柳州市供电局，广西 柳州 545000)

基于Mallat变换的时间序列模型在短期风速预测中的应用

王维志，陈海毅

(柳州市供电局，广西 柳州 545000)

短期风速预测对风电并网发电系统的运行具有重要的意义。为了提高风电场短期风速预测的精度，提出了基于Mallat变换的时间序列模型应用于风电场的短期风速预测。首先利用二进正交Mallat算法将随机非平稳原始风速序列进行多层分解和单层重构，分离出高频信息和低频信息；然后对分离出来的信息进行回归分析，分别建立ARMA-ARIMA模型进行预测；最后将预测结果进行叠加，得到原始序列的预测值。通过实例数据验证分析，结果表明该模型可以有效提高预测的精度，有一定的实用价值。

短期风速预测；Mallat变换；分解；重构；时间序列

1 引言

近年来，风力发电技术发展迅速，风能作为一种清洁可再生能源，已引起世界各国的广泛关注和深入研究。风力发电具有很强的随机性，风速预测是风电场规划设计的一项重要工作[1]。随着风能的加速发展，越来越多的大型风电场并网，风电在电网中的比重逐步增大，风电的随机波动性将增大调度的难度，风速的准确预测可以减少电力系统运行成本和旋转备用，提高风电穿透功率极限，有利于调度部门及时调整发电计划，从而减轻对电网的影响[2]。对风电场风速进行较为准确的预测，可以降低电网所需的储备电能，增加电网的可靠性[3]。目前，风速预测的方法有：神经网络法(ANN)[4]、支持向量机法[5]、模糊层次分析法[6]、时间序列法[7]以及各种方法组合的预测模型[8-9]等。由原始风速时间序列可以建立各种预测模型进行风速预测，这些模型的预测精度存在不同程度的差异。

风速具有很强的随机性和波动性，可以看作多个不同频率分量的叠加。对风速序列进行频域分解的基础上，根据频域分量的特点分别建模是提高预测精度的有效途径[9]。由于二进正交小波Mallat的时频窗口具有可调性，当尺度较大时，时频窗口的时域部分较宽、分析频率低；当尺寸较小时，窗口时频部分较窄而分析频率高，适合作细节观察。本文利用Mallat算法将原始风速时间序列进行多层分解和单层重构，然后对重构后的各层分量进行回归分析，分别建立ARMA-ARIMA模型进行预测，最后将预测结果叠加。算例采用某风电场的原始风速数据，利用MATLAB7.0和Eviews软件综合编程，实验结果表明，基于该方法的风速预测模型具有较高的预测精度，具有一定的实用价值。

2 二进正交小波Mallat算法

Mallat从空间概念方面形象地说明了多分辨分析特性，并结合了信号分解不同频率通道的算法和重构算法[10]。

(1) 分解算法

将待分解的离散信号设为co，根据分解算法有：

cj+1=Lcj,dj+1=Hdj,(j=0,1,…,J)

(1)

其中L和H分别为低通滤波器和高通滤波器；cj+1和dj+1分别为原始信号在分辨率2-(j+1)下的低频信号和高频信号，是原始信号在相邻不同频域段上的成分；J表示最大的分解层数，最终信号co分解为d1,d2,…,dJ和cJ。该分解算法利用二抽取，使每层分解比分解前的信号数据长度减半，而总输出数据长度与输入数据co长度保持一致，信号个数的减少对预测是不利的，但经过Mallat算法分解后的信号可以进行二插值重构。

(2) 重构算法

Mallat重构表达式为：

Cj=L*Cj+1+H*Dj+1,(j=J-1,J-2,…,0)

(2)

式中，L*和H*分别为L和H的对偶算子，用(2)式对分解后的信号进行重构可以增加信号的个数，对d1,d2,…,dJ和cJ分别进行重构，得到D1,D2,…,DJ和CJ，则有

X=D1+D2+…+DJ+CJ

(3)

其中，D1:{d11,d12,…},…,DJ:{dJ1,dJ2,…}为第1层至第J层的高频重构信号；CJ:{cJ1,cJ2,…}为第J层低频信号。在Mallat算法中利用二插值，即在输入数据序列每相邻数据之间补一个零，以使数据长度增加一倍，从而恢复到抽取前的数据长度。

3 时间序列预模型

风速是一种随机变量，Box Jenkins 方法是随机时间序列分析的主要方法之一，已被用于风速预测。它利用历史数据来建模，经过模型识别、参数估计、模型检验来确定一个能够描述所研究时间序列的数学模型，再由该模型推导出预测模型。

3.1 预测模型

(1)ARMA(Auto Regressive Moving Average)模型是一类常用的随机时间序列模型，序列的当前值是现在和过去的误差以及先前的序列值的线性组合。ARMA(p,q)用数学模型描述为：

(4)

(2) ARIMA(Auto Regressive Integrated Moving Average)模型是指将非平稳时间序列转化为平稳时间序列，然后将因变量仅对它的滞后值以及随机误差项的现值和滞后值进行回归所建立的模型。一个实际的时间序列通常是含有多种成分的非平稳序列，经过d阶差分后，{▽dyt}是一个平稳的ARMA序列，则

φp(B)▽dyt=θq(B)αt

(5)

为(p,d,q)阶累计式自回归滑动平均模型，即为ARIMA(p,d,q)，其中yt为原始序列，B为后移算子。

3.2 平稳性检验

时间序列的平稳性是建立ARMA模型的前提，平稳性检验最常用的单根检验方法有：DF检验、ADF检验、PP检验、DF-GLS检验等。本文采用ADF检验法，检验方程如下：(6)

▽yt=γyt-1+ξ1▽yt-1+…+ξp-1▽yt-p+1+εt

(6)

式中p值视具体情况而定，一般选择保证εt是白噪声的最小p值，实际操作常借用赤池信息准则(AIC)进行判断。

3.3 模型识别和模型定阶

在ARMA模型的识别过程中，利用表1的性质，然后再根据自相关函数(简称ACF)、偏自相关函数(简称PACF)以及它们各自的相关图(即ACF、PACF相对于滞后长度描图)确定时间序列所采用的模型以及初步粗略确定ARMA(p,q)模型中的p和q的阶数。

3.4 参数估计

时间序列参数估计主要方法有：最大似然估计法、最小二乘估计法、偏最小二乘估计法等，本文采用最小二乘估计法进行参数φi(i=1,2,…,p)，θj(j=1,2,…,q)估计，使残差的平方和达到最小。

表1 时间序列模型识别准则

3.5 模型检验

(7)

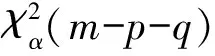
(2)采用AIC准则函数定阶，使准则函数达到极小是最佳模型。AIC函数定义为：

(8)

式中：L是对数似然数；n为观测数目；p和q是模型阶数。p和q的值由小到大逐步测试验证，当AIC最小时，综合考虑其他检验值，确定最终模型的阶数。

(3)平稳可逆性检验：当φ(B)=0以及θ(B)=0方程的根都在单位圆内时，满足稳定性和可逆性。

图1 预测模型的步骤

4 基于Mallat变换的时间序列模型

(9)

4.1 基于Mallat变换的时间序列预测步骤

4.2 误差评价指标

误差评价指标可以直接反映预测值与实际值的差异程度，同时反映各种模型的好坏。本文分别采用平均绝对误差(MAE)、均方根误差(RMSE)、平均百分比误差(MAPE)来评价和比较各个模型的预测值与实际值的差异程度。

(10)

(11)

(12)

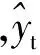
5 实例分析

本文以某风电场每小时测量一次的风速序列为算例，取2010年4月1日1:00:00时刻到4月11日10：00：00时刻250个风速数据，前200个风速数据作为训练样本，记为序列{yt}，后50个数据用作测试样本。原始风速序列如图2所示。

图2 原始风速数据

首先利用db3小波对训练样本序列{yt}进行3层分解，然后对分解后得到的低频信号c3和高频信号d1,d2,d3分别进行Mallat单层重构，得到C3和D1,D2,D3。原始风速训练样本经过Mallat分解和重构后的结果如图3所示。

由Mallat多层分解和重构的结果进行回归分析，分别建立ARMA/ARIMA模型进行估计预测。以分解重构后得到的低频信号C3为例，进行回归分析建模。由时间序列建模预测的步骤，先对C3进行ADF平稳性检验，利用Eviews软件测试，结果如表2所示。

表2 ADF检验结果

由表2可知，C3序列ADF检验统计量比10%的显著水平的临界值还大，所以在95%置信水平下有理由接受原假设，即C3序列是非平稳的，不满足ARMA建模的前提。对非平稳序列C3进行一阶差分再进行ADF检验，由检验结果可知，差分后的序列变得平稳。

图3 原始风速分解重构结果

对差分处理得到的平稳序列进行模型识别和定阶。求出平稳序列的自相关函数以及偏相关函数如图4、图5所示，可知ACF和PACF都是拖尾的，利用模型识别准则进行判断，该平稳序列选用ARMA模型；同时由下图的滞后阶数，初步判断模型为ARMA(2,4)。

图4 自相关函数

图5 偏相关函数

利用最小二乘估计法对模型ARMA的参数进行估计，并结合考虑模型检验中的各项指标参数，进行比较验证，最后确定模型的为ARMA(2,6)。模型检验结果：检验残差序列的自相关函数与零无显著差异；AIC准则函数值为1.566971；方程φ(β)=0的根分别为：0.53-0.1i，0.53+0.1i以及方程θ(B)=0的根分别为0.65-0.38i，0.65+0.38i，0.75i，-0.75i，0.65-0.38i，0.65+0.38i都在单位圆内。残差序列的平方和最小为0.2735。由以上结果分析可得，原始非平稳序列C3的回归预测模型为ARIMA(2,1,6)。

重构后得到的高频分量D1,D2,D3的回归预测模型的建立与上述步骤相同，详细过程不再重述；一层高频信号D1的回归预测模型为ARMA(5,1);二层高频信号D2的回归预测模型为ARMA(4,3)；三层高频信号D3的模型为ARIMA(1,1,3)。将上述得到的回归模型分别进行滚动预测，预测将来50小时内每小时的风速，最后将预测结果进行叠加。同时，对原始风速序列{yt}不经Mallat分解直接进行时间序列回归建模，最终模型为ARIMA(2,1,1)，利用该模型进行预测，预测结果与经过Mallat变化的预测结果进行比较，如表3所示。

表3 预测结果比较

由表3的预测结果与误差分析可知，利用二进正交Mallat算法对原始风速时间序列进行变换再分别建立预测模型，预测结果的MAE为0.4713m/s，RMSE为0.5815m/s，MAPE为10.7447%比直接用时间序列模型对原始风速序列进行预测的预测精度提高一倍左右，预测效果较好，具有实际可行性。从图6也可以看出，Mallat小波变换预测模型的拟合效果要优于直接用时间序列建立的模型。

图6 两种方法预测结果曲线

6 结论

本文将二进正交Mallat算法与时间序列预测方法相结合，先利用Mallat算法将原始风速序列多层分解和单层重构，再将分离出来的低频信号和高频信号分别进行回归分析，建立ARMA/ARIMA模型进行估计预测。文中详细阐述了Mallat分解与重构算法以及利用时间序列建立模型的步骤，最后通过实例分析，实验结果表明，本文提出的基于Mallat变换的时间序列模型应用于短期风速预测比直接对原始风速数据建立的时间序列模型有更好的预测效果，预测精度有很大的提高，具有一定的实际可行性。

[1] 常太华,王璐,马巍.基于AR、ARIMA模型的风速预测[J].华东电力,2010,38(1):59-62.

[2] 蒋金良,林广明.基于ARIMA模型的自动站风速预测[J].控制理论与应用,2008.25(2):374-376.

[3] 郭鹏.双自回归滑动平均模型风速预测研究[J].现代电力,2009,26(6):66-69.

[4] 梁岚珍,邵璠.时序神经网络算法的短期风速预测研究[J].控制工程,2011,18(1):43-50.

[5] 彭怀午,杨晓峰,刘方锐.基于SVM方法的风电场短期风速预测[J].电网与清洁能源.2009,25(7):48-52.

[6] 黄文杰,傅砾,肖盛.采用改进模糊层次分析法的风速预测模型[J].电网技术,2010,34(7):164:168.

[7] 邵璠,孙育河,梁岚珍.基于时间序列法的风电场风速预测研究[J].华东电力,2008,36(7):26-29

[8] 蔡凯,谭伦农,李春林,等.时间序列与神经网络法相结合的短期风速预测[J].电网技术,2008,32(8):82-90.

[9] 王晓兰,王明伟.基于小波分解和最小二乘支持向量机的短期风速预测[J].电网技术,2010,34(1):179-184.

[10] Stephane G M.A theory for multiresolution signal decomposition;The wavelet representation[J].IEEE Tran on Pattern Analysis and Machine Intelligence,1989,11(7):674-693.

Application for Short-term Wind Speed Forecast Based on Time Series Model of Mallat Transformation

WANGWei-zhi,CHENHai-yi

(Liuzhou Power Supply Bureau,Liuzhou 545000,Guangxi Zhuang Autonomous Region,China)

Short-term wind speed forecast has important meaning for the operation of the power system with wind power connected to it.In order to improve the precision of short-term wind speed forecast,the time series model for short-term wind speed forecast based on Mallat transformation is proposed.Multilayer decomposition and single layer reconfiguration have been applied in dealing with random non-stationary original wind series by using Mallat algorithm，separate high and low frequency information out;then do regression analysis for those information，ARMA-ARIMA model is created for forecasting;accumulate the forecasted results to get the predictive value of original series.Verified by living examples,the method of this paper can improve the forecast precision and have certain practical value.

short-term wind speed forecast;Mallat transformation;decomposition;reconfiguration;time series

1004-289X(2015)03-0094-05

TM76

B

2015-05-12

王维志(1986-)，男，柳州供电局。