On the Tangent Bundle of a Hypersurface in a Riemannian Manifold∗
2015-06-01ZhonghuaHOULeiSUN
Zhonghua HOU Lei SUN
1 Introduction
Let(M,g)be a Riemannian manifold,and TM be the tangent bundle of M.Let Gsbe the Sasaki metric on TM introduced by Sasaki[13]in terms of g.
The geometry of(TM,Gs)and the unit tangent sphere bundle(S(TM),Gs)have attracted many mathematicians in the last decades.Kowalski[5]showed that if(TM,Gs)is locally symmetric,then the base metric is flat and so does Gs.Musso and Tricerri[9]proved that(TM,Gs)has constant scalar curvature if and only if(M,g)is flat.Nagano[10],Tachibana and Okumura[15]studied the almost complex structure on(TM,Gs).Nagy[11]studied the geometry of the unit tangent sphere bundle of a surface.Klingenberg and Sasaki[2]showed that(S(TS2(1)),Gs)is isometric to the elliptic space of curvatureNagy[12],Sasaki[14],Konno and Tanno[3–4]studied the geodesics and Killing vector fields on(S(TM),Gs).Tashiro[16–17]studied the contact structure on S(TM).
Deshmukh,Al-Odan and Shaman[1]considered an orientable hypersurface Mnof the Euclidean space Rn+1and observed that the tangent bundle TM of M is an immersed submanifold of the Euclidean space R2n+2.They obtained expressions for the horizontal and vertical lifts of the vector fields on M and showed that the induced metric on TM is not a natural metric in general.In the special case that the induced metric on TM becomes a natural metric,they proved that the tangent bundle TM is trivial.
In this paper,we suppose that Mnis a hypersurface of a Riemannian manifold(Nn+1,G).We use the moving frame method to study the geometry of the tangent bundle TMnwith the induced metric from(TN,Gs).
In Section 3,we study the extrinsic geometry of TMnin(TNn+1(c),Gs)where Nn+1(c)is a space form of constant curvature c.In Section 4,we study the integrability of the almost complex structure J on TM and the K¨ahlerian form ω on TM induced by J.
2 Preliminaries
Suppose that(N,G)is an(n+1)-dimensional Riemannian manifold.Let D be the Levi-Civita connection in N,and π :TN →N be the natural projection.Through out this paper,we use the Einstein convention and the following ranges of indices:
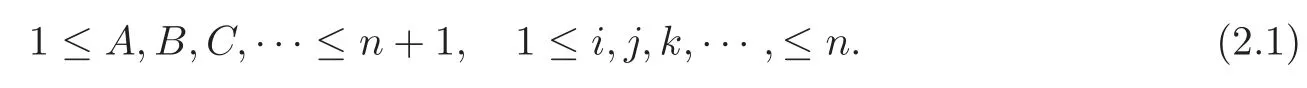
Let({yA})and({yA},{vB})be local coordinate systems in N and TN,respectively.Denote
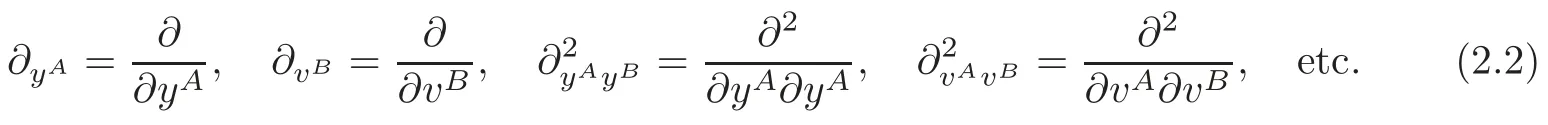
At first,we introduce the following lemmas.
Lemma 2.1(cf.[5])Let(N,G)be a Riemannian manifold and Y ∈ Γ(TN)be a vector field on N which is locally represented byThen the vertical and horizontal lifts YVand YHof Y over TN are given by
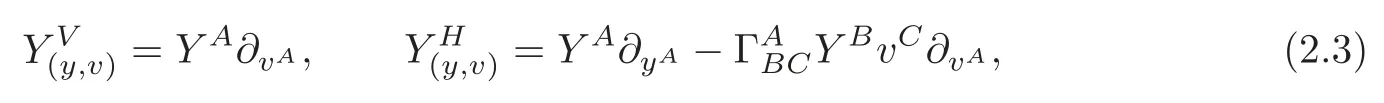
respectively,whereare the Christo ff el symbols of D.
Lemma 2.2(cf.[5])The Lie bracket of vector fields over TN is completely determined by
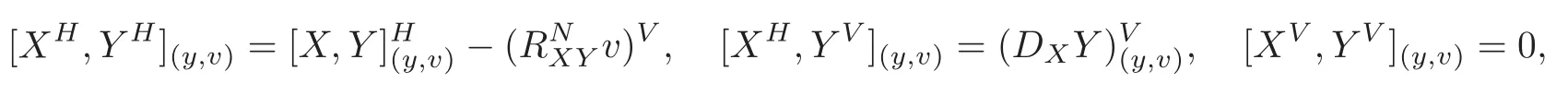
where X,Y ∈ Γ(TN)andis the Riemannian curvature operator of N.
The Sasaki metric Gson TN can be described as follows.
Definition 2.1(cf.[13])Let(N,G)be a Riemannian manifold.The Sasaki metric Gson TN is defined by

for any point(y,v)∈TN and vectors X,Y∈TyN.
By direct computation,we have the following lemma.
Lemma 2.3(cf.[7])Let(N,G)be a Riemannian manifold,and TN be the tangent bundle with the Sasaki metric Gs.Then the Levi-Civita connectionon(TN,Gs)is determined by

for any point(y,v)∈TN and vectors X,Y∈TyN.
3 Geometry of the Tangent Bundle of a Hypersurface
Suppose that f:Mn→Nn+1is a smooth immersion from Mninto Nn+1.Let
df(x):TxM→Tf(x)N
be the differential map of f at any x∈M.We define the smooth immersion F:TM→TN to be

for any point(x,u)∈TM.
Lemma 3.1Suppose that h and ν are the second fundamental form and the unit normal vector field of M in N,respectively.Let Xhand Xvbe the horizontal and the vertical lifts of X ∈ Γ(TM)onto TM,respectively,with respect to g=f∗G.Then the differential map dF of F is defined by

for any point(x,u)∈TM and the vector field X ∈ Γ(TM).
ProofFor any(x,u)∈TM,we have F(x,u)=(f(x),df(x)u)∈TN.Let()andbe the local coordinates around(x,u)and F(x,u).Letbe the Levi-Civita connection of the induced metric g.Then the local representation of f(x) is of the form
(f1(x1,···,xn),···,fn+1(x1,···,xn)).
Moreover,we have
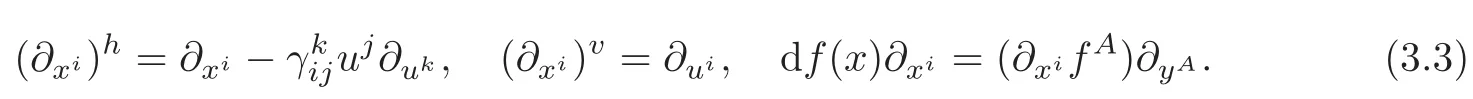
Therefore,
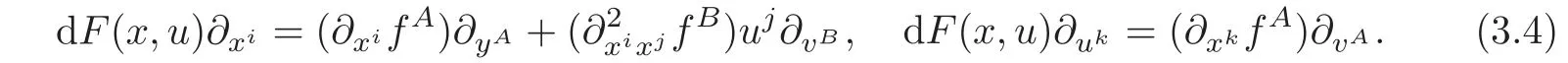
It follows from(3.3)–(3.4)that
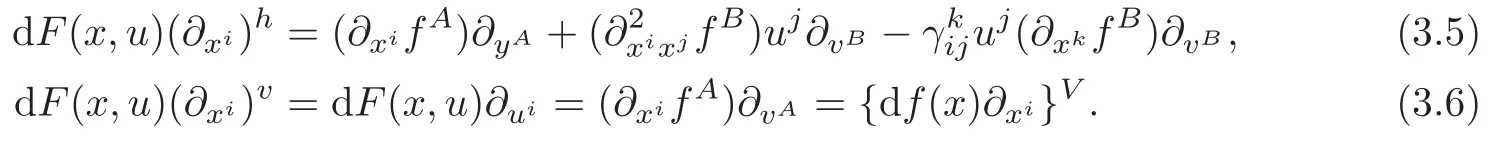
On the other hand,from Lemma 2.1,we have

Therefore,
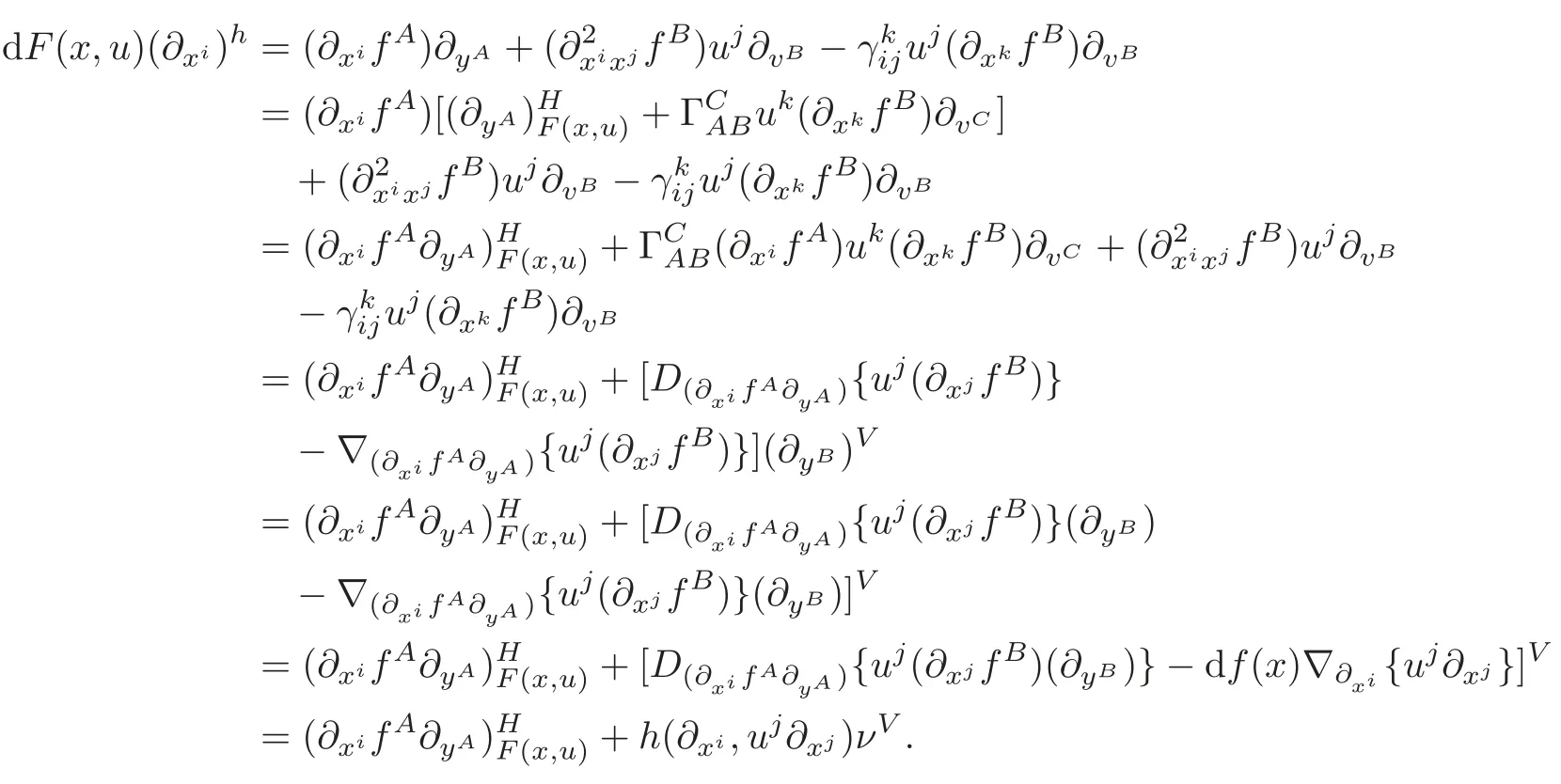
It follows from(3.3)that

Lemma 3.1 follows immediately from(3.6)and(3.8).
From Lemma 3.1,we have the following lemma.
Lemma 3.2Denote=F∗Gs.Then at any point(x,u)∈ TM,we have
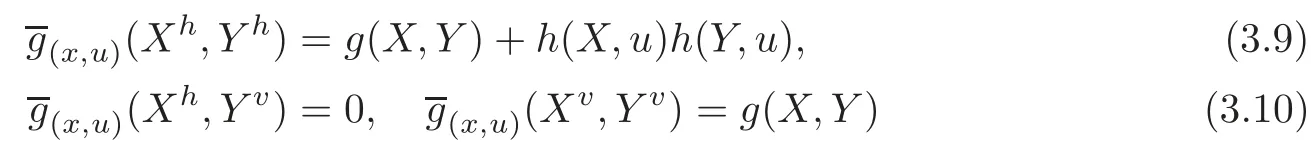
for any X,Y ∈ Γ(TM).
Remark 3.1From(3.9)of Lemma 3.2,we can see that(TM,g)is not a natural metric.
Suppose that(Nn+1(c),G)is a space form of constant section curvature c.The Riemannian curvature operator of(Nn+1(c),G)is given by
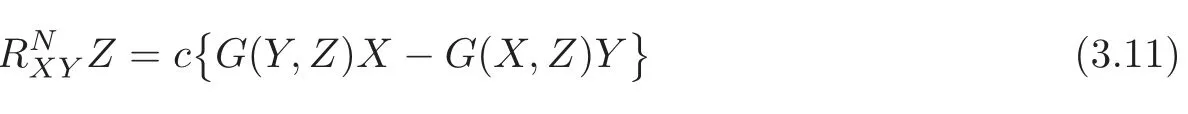
for any X,Y,Z∈Γ(TN).
Suppose that f:(M,g)→(Nn+1(c),G)is an isometrical immersion of Mninto Nn+1(c).Let A be the shape operator of M in Nn+1(c).Consider F:(TM,g)→(TNn+1(c),Gs)defined by(3.1).Then TM is a submanifold of TN with codimension 2.
In the sequel,we proceed to study the extrinsic geometry of TM in(TNn+1(c),Gs).
The two local orthonormal normal vector fields ν1,ν2of TM in TNn+1(c)are given by
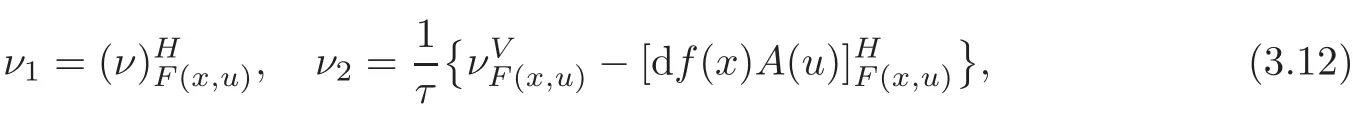
where τ2=1+g(A(u),A(u))with τ>0 at any point(x,u) ∈ TM,so that the normal bundle T⊥(M)of TM in TN is locally spanned by ν1and ν2.
From now on,we denote brie fly X:=[df(x)X]f(x)and
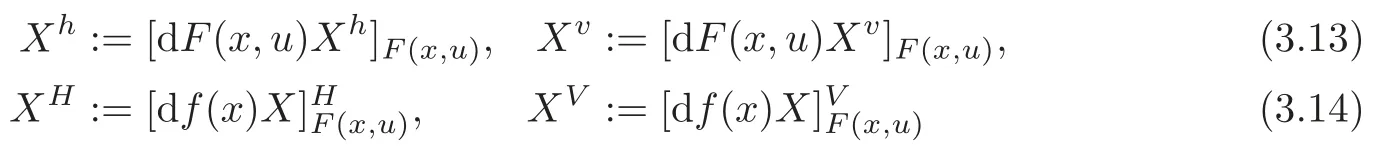
for any X∈TxM.
Let{e1,···,en}be a local orthonormal frame field on(M,g),and{θ1,···,θn}be its dual frame field.We denote

for any u=Γ(TM).It follows from(3.9)that
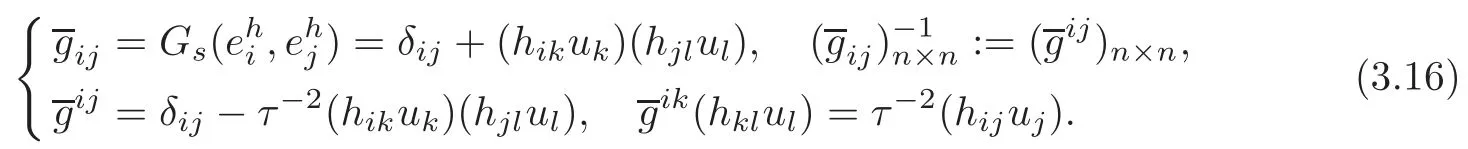
Moreover,(3.2)and(3.12)turn into
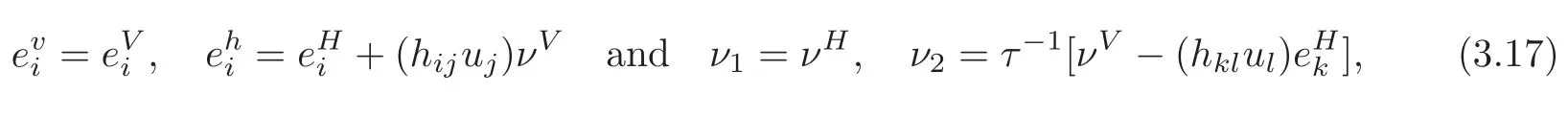
respectively.From(3.17),we obtain
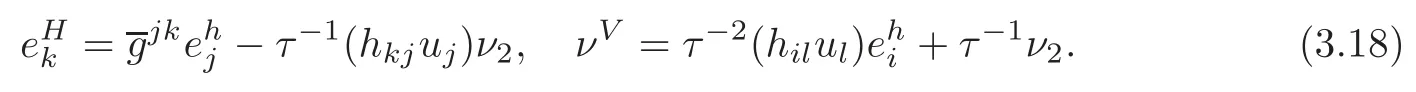
Using(3.11),from Lemma 2.3,we have
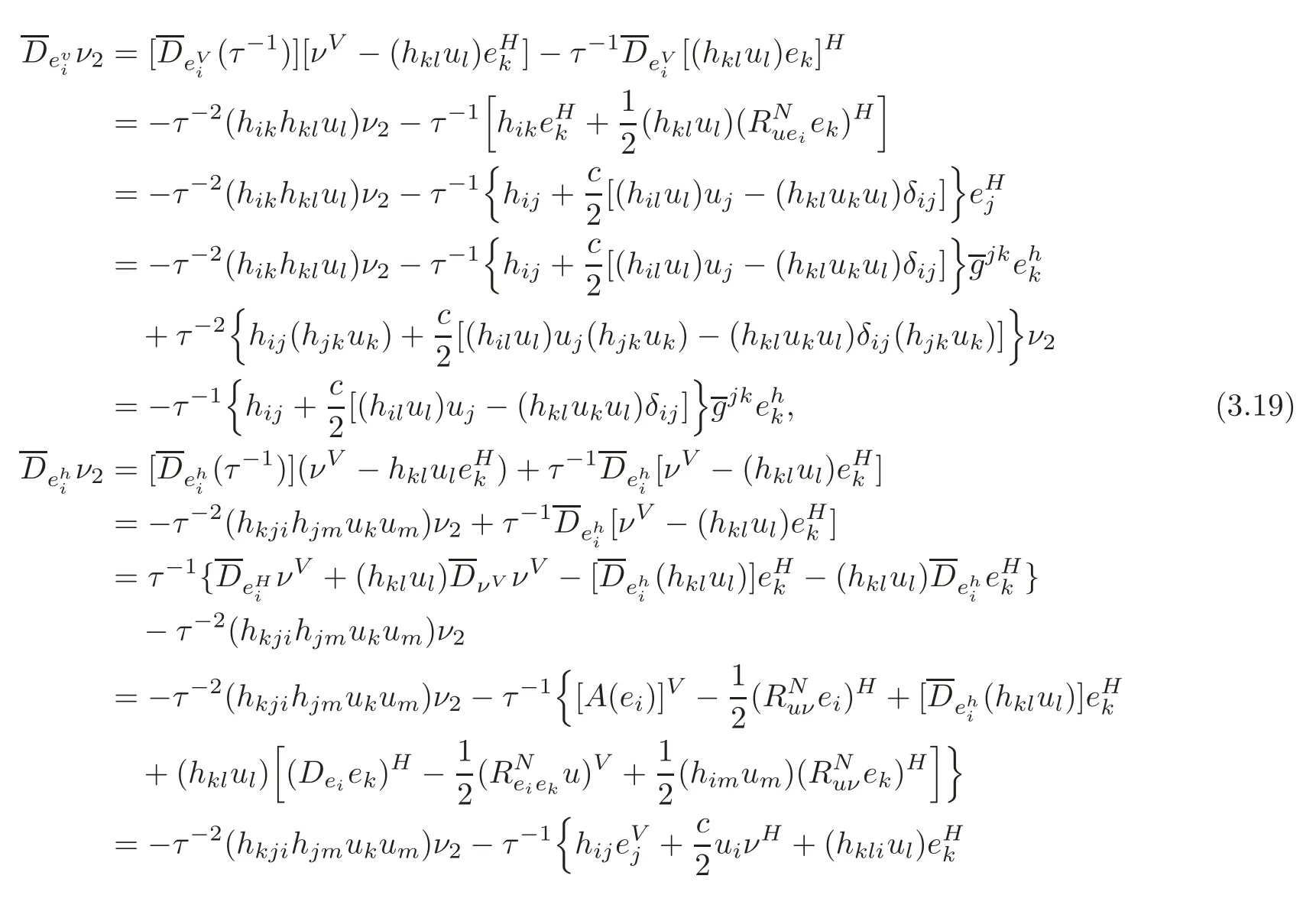
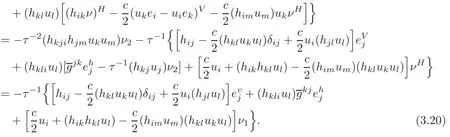
Moreover,we also have
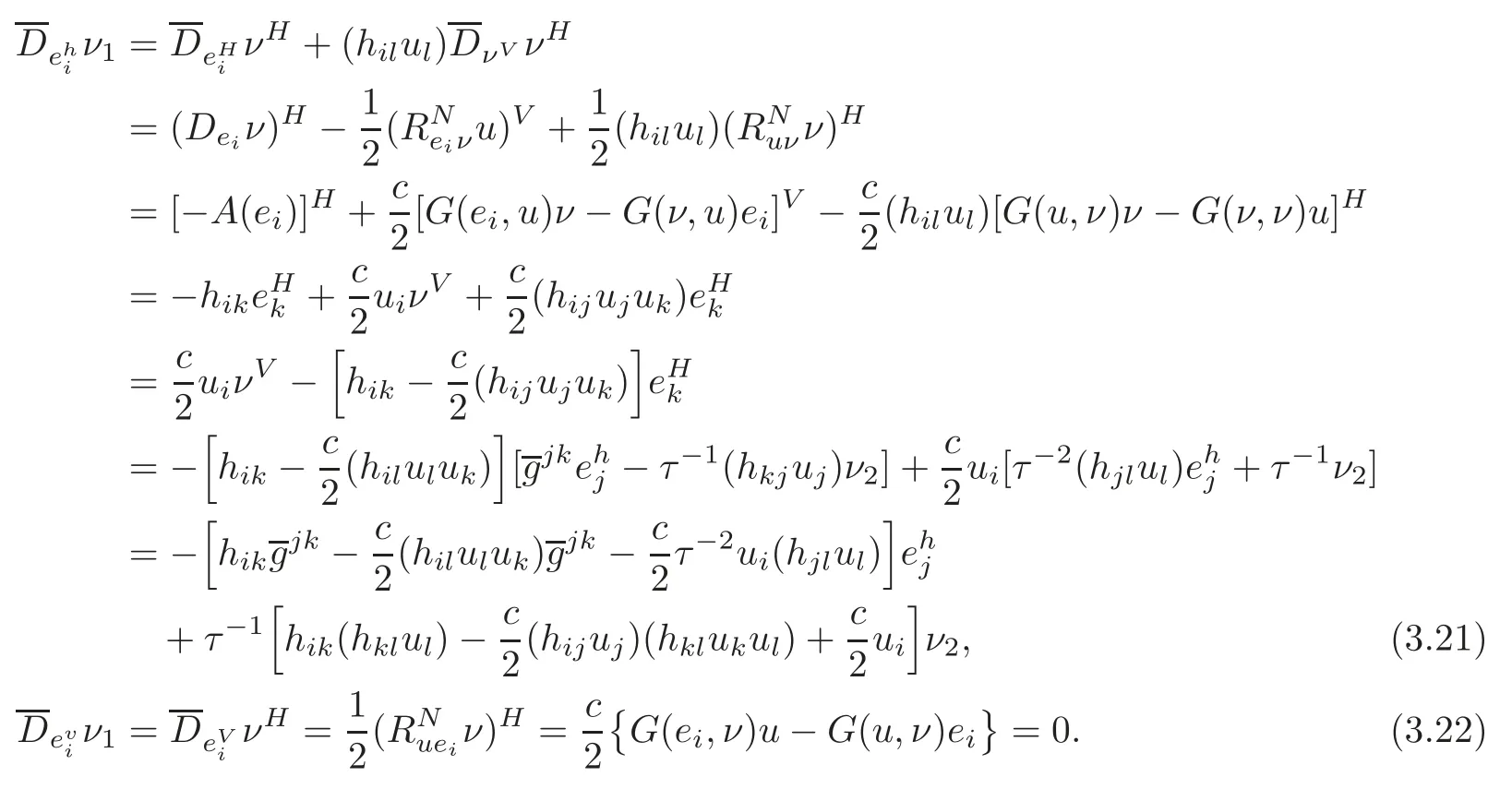
From(3.19)–(3.20),we can see that
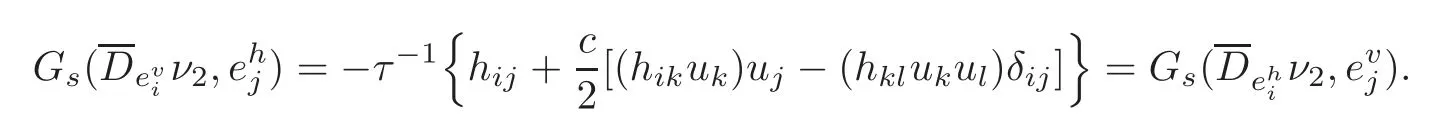
From(3.19)to(3.21),we immediately obtain the following proposition.
Proposition 3.1Let∇⊥be the normal connection of(TM,)in TNn+1(c).Then

where for any 1≤i≤n,
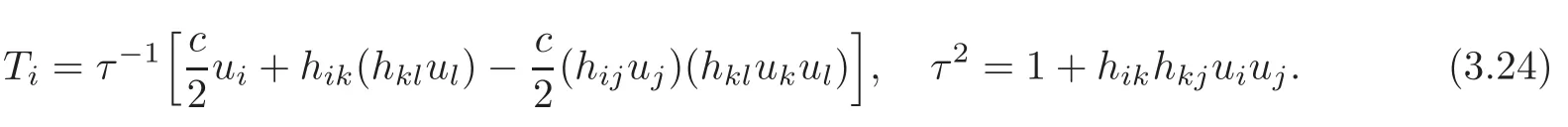
ProofSince{ν1,ν2}is a local orthonormal frame field of T⊥M,we have
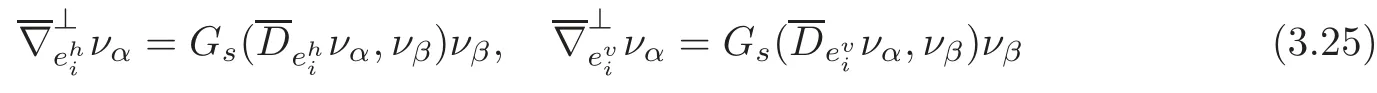
for any 1 ≤ i≤ n and α =1,2.Substituting(3.19)–(3.21)into(3.25),we obtain(3.23).The proof of Proposition 3.1 is completed.
From(3.19)–(3.21),we can immediately obtain the following lemma.
Lemma 3.3Denote byαthe shape operator of TM with respect to ναfor α =1,2.Then
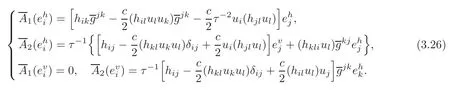
Using Lemma 3.3,we can prove the following proposition.
Proposition 3.2The second fundamental form σ of TM is determined by
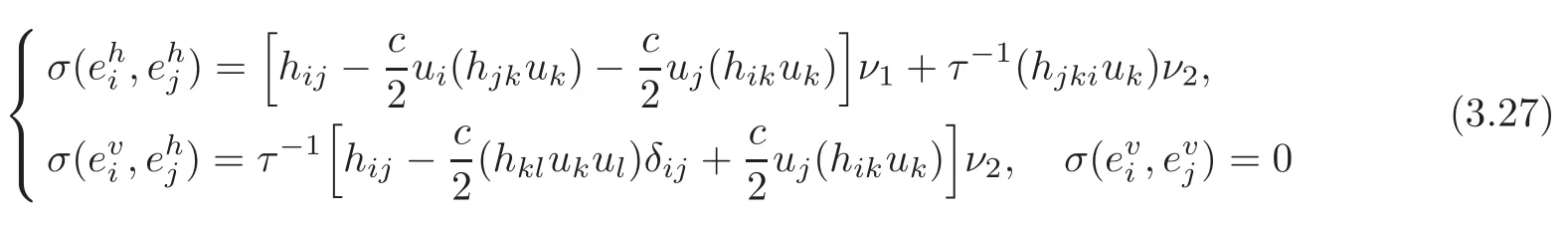
for any 1≤i,j≤n.

ProofIt is well-known that σ = σανα,where for any,∈Γ(TF(x,u)TM).Substituting(3.26)into(3.28),we obtain.
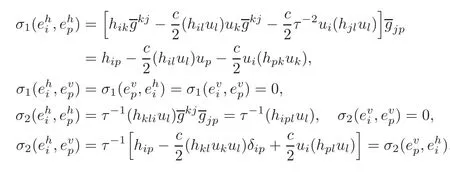
This completes the proof of Proposition 3.1.
Theorem 3.1Let Mnbe an immersed hypersurface of a space form Nn+1(c).Denote bythe mean curvature vector field of TM in TNn+1(c).Suppose that the length ofis invariant along every fibre of TM.Then we have that
(1)If c≥0,M is totally geodesic in Nn+1(c).
(2)If c<0,M is an isoparametric hypersurface with at most three distinct principal curvatures{−√−c,0,√−c}with multiples{m−,m0,m+},whose second fundamental form is parallel.
ProofLetbe the mean curvature vector field of TM.Choose{ei}such that hij= λiδij.Then it follows from Proposition 3.2 that
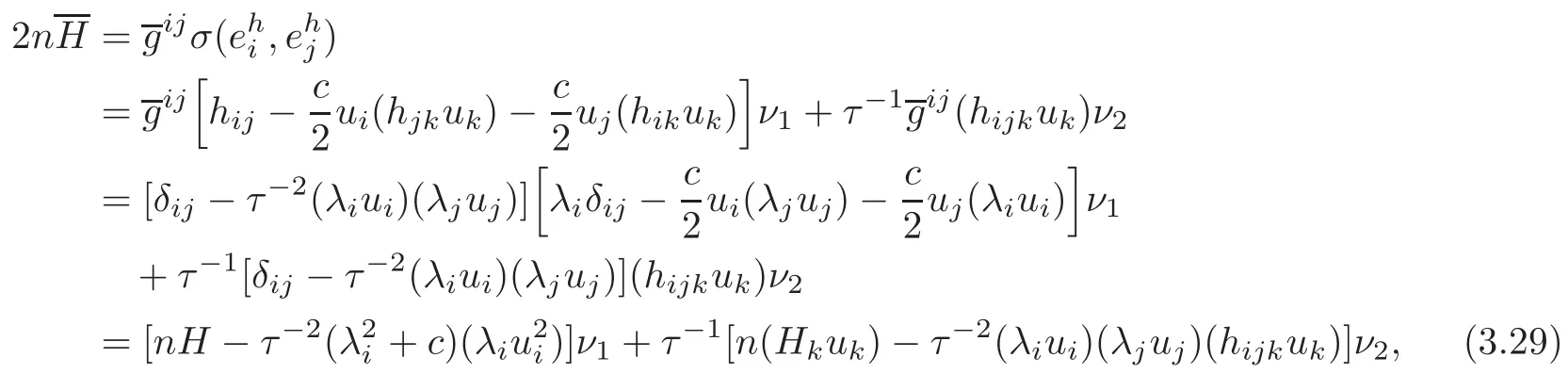
where H is the mean curvature of M,and{Hk}are the coefficients of the covariant derivative of H.Taking the squared length on both sides of the above equation,we obtain
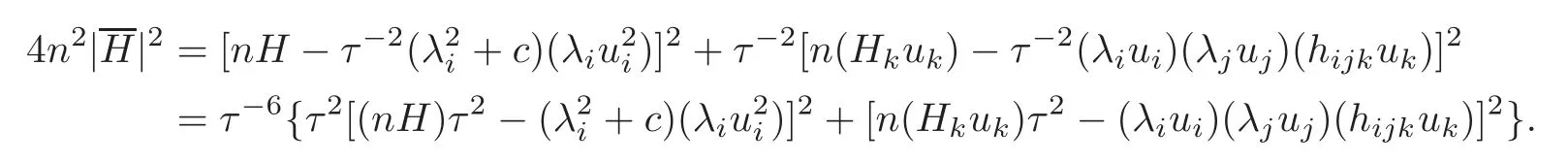
Since the length ofis invariant along the fibres,by the above equation,we have
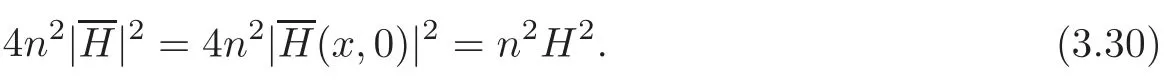
It follows that
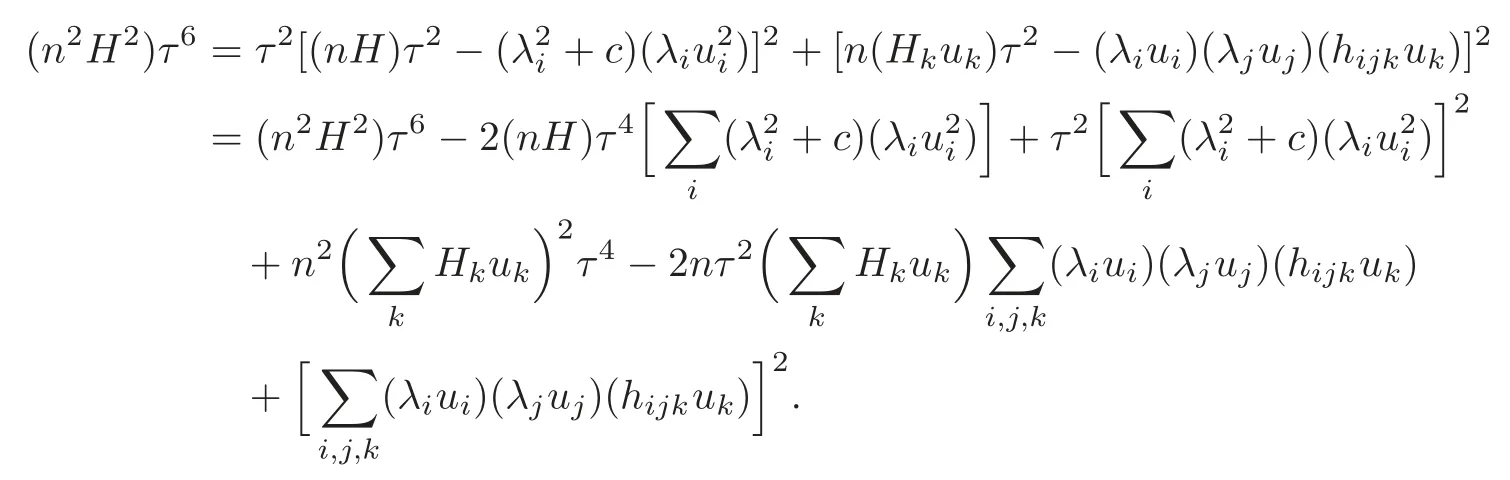
So we have
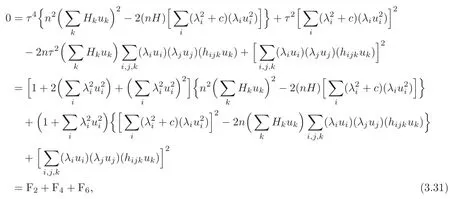
where

From(3.31),we have F2=F4=F6=0 for any(u1,···,un),which is equivalent to
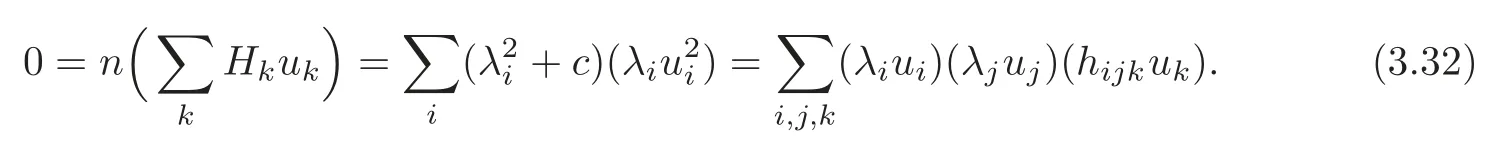
From the first equality of(3.32),we have Hk=0 for any 1≤k≤n,which means that M is of the constant mean curvature.
The second equality of(3.32)implies that λi(+c)=0 for any 1 ≤ i≤ n.It follows that every principal curvature λiis constant for all 1 ≤ i≤ n.
When c≥ 0,λi=0,for all 1≤ i≤ n.In this case,Mnis totally geodesic in Nn+1(c).
When c<0,λi=0,−√−c or√−c.We suppose that λi=0 for 1≤ i≤ m0,λi= −√−c for m0+1≤i≤m0+m−and λi=−√−c for m0+m−+1≤i≤m0+m−+m+=n.
The third equality of(3.32)turns into

It follows from the above equality and the assumptions that
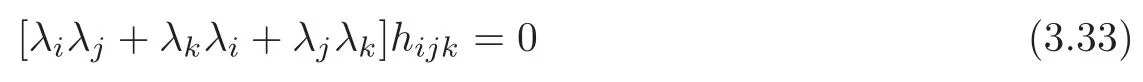
for any 1≤i Suppose that 1≤i≤j≤k≤n.It is seen from(3.34)that hijk=0,and now that i,j or j,k lie in the same range of indices.For i,j,k lying in the di ff erent ranges of indices,from(3.33),we have hijk=0.It follows that hijk=0 for any 1≤i,j,k≤n,which means that Mnhas a parallel second fundamental form in Nn+1(c).This completes the proof of Theorem 3.1. Remark 3.2Miyaoka[6]studied the geometries of isoparametric hypersurfaces with at most three distinct principal curvatures in a space form Nn+1(c)of the constant curvature c with c≥0.Our result gives a geometrical description of this kind of hypersurfaces with c<0. By Theorem 3.1,we immediately obtain the following corollary. Corollary 3.1Let Mnbe a smooth hypersurface of a space form Nn+1(c)with c≥0.Then the following statements are equivalent: (1)The length of the mean curvature fieldof TM is invariant along the fibres of TM; (2)TM is totally geodesic in(TNn+1(c),Gs); (3)TM is minimal in(TNn+1(c),Gs); (4)M is totally geodesic in Nn+1(c). Munteanu[8]computed the Riemannian curvature tensor of TN endowed with the general metric Ga,b.For(TNn+1(c),Gs),we have the following lemma. Lemma 3.4(cf.[8])Suppose that(Nn+1(c),G)is a space form of the constant sectional curvature c.Then the Riemannian curvature tensorof(TNn+1(c),Gs)is given by for any X,Y,Z∈Γ(TN)at point(y,v)∈TN. By direct computation,we obtain the following lemma. Lemma 3.5Let Mnbe a hypersurface of(Nn+1(c),G).Let{e1,···,en}be a local orthonormal frame field on M,and ν be the unit normal vector field of M.Then where V=and Lemma 3.6Under the assumptions as in Lemma 3.5,suppose in addition thatand{ν1,ν2}are chosen as in(3.17).Then we have Denote bythe Riemannian curvature tensor and by⊥the normal curvature tensor of TM in TNn+1(c).Then we have the following Gauss-Codazzi equations: for any X,Y,Z ∈ Γ(T(TM))and ξ∈ Γ(T⊥(TM)). By Proposition 3.1,we have the following theorem. Theorem 3.2Let Mnbe a smooth hypersurface of a space form Nn+1(c).If the normal bundle of TM in TN is flat,then Mnis flat and totally geodesic in Nn+1(c),and vise versa. ProofLet{e1,···,en}be a local orthonormal frame field on M such that hij= λiδij.Then(3.16)and(3.26)–(3.27)turn into where Since the normal curvatures of TM are determined by it follows that the normal bundle of TM is flat in TN if and only if for any(x,u)∈TM and 1≤i,j≤n.From the Wiengarten formula(3.43),we have Using(3.41)and(3.44),we havefrom which we get It follows that By a direct but not difficulty computation,we can see that Substituting(3.49)–(3.50)into(3.47)and sorting it,we get for all 1≤i,j≤n.From(3.48)and(3.51),we obtain for all 1 ≤ i,j≤ n.Suppose in(3.52)that u=ukek=0,and fromat any point x∈M for all 1≤i,j≤n,we have+c=0 at any x∈M for all 1≤i≤n,which implies that Nn+1(c)is of the non-positive curvature.Suppose in(3.52)that δij=1 and c<0,i.e.,λi≠0 at any x∈M for all 1≤i≤n,and we have that which implies that λi=0 at any x ∈ M for all 1 ≤ i≤ n.It is contradictory to our assumption,and we have that=0 at any point x∈M for all 1≤i,j≤n if and only if M is flat and totally geodesic in Nn+1(c).It is seen from(3.53)that,in this case,=0 for all 1≤i,j≤n. The reverse is trivial.This completes the proof of Theorem 3.2. In this section,we study the almost complex structure J on TM,which is compatible withand the K¨ahlerian form ω on TM induced by J. Let{e1,e2,···,en}be a local orthonormal frame field and{}be the associated connection forms on M.We describe the almost complex structure J on TM as follows: where α,β,γ and ρ are the smooth functions on TM to be determined.Since J is compatible with,we have Substituting(4.1)into(4.2),we get Thus,J is determined by for any 1≤i≤n. The Nijenhuis tensor of J is defined to be NJ(X,Y)=[X,Y]+J[JX,Y]+J[X,JY]−[JX,JY] for any X,Y ∈ Γ(T(x,u)TM).It is easy to see that NJ(Y,X)=−NJ(X,Y),NJ(X,Y)=−NJ(JX,JY),NJ(X,Y)=JNJ(JX,Y). Therefore,we have NJ(Xv,Yv)=−NJ(JXv,JYv),NJ(Xv,Yh)=JNJ(JXv,Yh) for any point(x,u)∈TM and X,Y∈TxM.Since J is an isomorphism from H(x,u)to V(x,u),it follows that J is integrable if and only if NJ(Xh,Yh)=0 for any X,Y∈Γ(TM). Let us computefor any 1≤i≤n.It is known that from which we have At first,we have From the Definition of,we can see that Substituting(4.7)into(4.6)and using(4.5),we obtain Using(4.8)–(4.9),we have where we have used Therefore, It follows that Since=0,we have It follows that for any differentiable function ϕ on TM, By using(4.12),we have and Substituting(4.13)–(4.15)into(4.11),we obtain It follows from(4.5),(4.10)and(4.16)that where Theorem 4.1Let Mnbe a smooth hypersurface of Nn+1,and J be the almost complex structure on(TM,).Then J is integrable if and only if M is flat and is locally a product of a part of the principal curvature line and a piece of the(n−1)-dimensional totally geodesic submanifold of Nn+1. ProofFrom(4.17),one can see that J is integrable if and only ifat any point(x,u)∈TM for any 1≤i,j,k≤n. Let{ei}be a local orthonormal frame field on M such that hij= λiδij.ThenIt follows from(4.12)that for any 1≤l,p≤n.Therefore,we have for any 1≤l≤n,that Suppose thatfor any 1≤i,j,k≤n at any point(x,u)∈TM.Then()=0 for any 1≤i,j,k,l≤n at any point(x,u)∈TM. Computingand putting u=0,we get for any 1≤i,j,k,l≤n at any point x ∈ M.Substituting(4.23)into(4.19),we obtain At the point x∈M where(4.24)is trivial. Suppose thatat the given point x∈ M.For u ∈ TxM with τ≠1,we have Multiplying λkukon both sides of(4.25)and taking sum with respect to k,we obtain It follows that Substituting(4.26)into(4.25),we get for any i≠j.Suppose that λ1≠0.Then from(4.27),we have for any j>1.The condition that τ≠1 implies that It follows from(4.28)thatλ1u1≠0.Taking j=1 in(4.27),we obtain that λi=0 for any i>1. So there is at most one nonzero principal curvature of the shape operator A at any point of M.It follows that for any i≠j and k≠l,which together with(4.23)implies that=0 for any i≠j and k≠l,which implies that M is flat. Suppose that=0 for any 1≤i,j,k≤n at any point(x,u)∈TM.Then(4.18)turns into or equivalently for any fixed 1≤ i,j,r≤ n.Denote Λij=hpijup.Then(4.29)turns into for any fixed 1≤i,j,r≤n with i≠j. At the point x∈M where(4.30)is trivial.At the point x ∈ M where λk≠for some 1 ≤ k ≤ n,we can suppose that λ1≠0 and λk=0 for 2≤ k ≤ n. Suppose that i=1 in(4.30).Then for any fixed 1 for any fixed 1 for all 1 ≤ i,j,k ≤ n where λj,k=ek(λj).It follows from(4.33)that for any 1 which implies that for all 1 for all 1≤ j,k ≤ n.It follows from(4.36)–(4.37)that for any 1 Taking the partial derivative on both sides of(4.39)with respect to u1and using(4.20),we have It follows from(4.36)and(4.39)–(4.40)that for all 1 for all 1 for all 1 Let γ be a part of the curvature line with respect to the principal curvature λ1and Un−1be the maximal integral submanifold of Ln−1through every point of γ.Then it follows from(4.36)that Un−1is totally geodesic in Nn+1.The second equality of(4.41)implies that Mnis locally a Cartesian product of γ and Un−1. The proof of sufficiency is trivial.This completes the proof of Theorem 4.1. It is known that the Khlerian 2-form ω of TM is defined to be for all vector fields,∈(TM),where J is determined by(4.4).Let{e1,e2,···,en}be an orthonormal frame on M such that hij= λiδij.By direct computation,we have It is known that the exterior differential of ω is defined by for all vector fields,,∈(TM). By using(4.5),we have Theorem 4.2Suppose that Mnis a smooth hypersurface of Nn+1and ωis the K¨ahlerian2-form on(TM,g,J).If(TM,g,J,ω)is almost K¨ahlerian,then M is locally a product of a part of the principal curvature line and a piece of the(n−1)-dimensional totally geodesic submanifold of Nn+1. ProofBy Definition,(TM,g,J,ω)is almost K¨ahlerian if dω=0 onTM,which implies that the right-hand sides of(4.50)–(4.53)are zero. We suppose that dω=0 onTM.From(4.52),we have for any fixed j≠k and all(x,u)∈TM. Choose uk=1 and uj=0 in(4.54)for any other j≠k.Then it follows that which implies that there is at most one nonzero principal curvature at any x∈M,whose multiple is 1.When λ1= ···= λn=0 at x ∈ M,the right-hand sides of(4.50)–(4.53)are identically zero.Without loss of generality,we suppose that λ1≠0 and λk=0 for all 2 ≤ k ≤ n in an open subset W of M.From(4.51),we have for all 2≤j,k≤n at any(x,u)∈TM where x∈W.It follows immediately from(4.55)that for all 1≤i≤n and 2≤j,k≤n.Substituting(4.56)with i=1 into(4.56),we obtain from which we have for all 2≤j,p≤n at any(x,u)∈TM where x∈M and u∈TxM with u1≠0.Let u1tend to 0 in(4.59)and(4.60).It follows that Substituting(4.61)into(4.59)and(4.60),and using(4.61)once more,we obtain for all 1≤i≤n and 2≤j≤n at any x∈W.It follows from(4.57)and(4.62)that all of hijk’s are zero except for h111.Note that for hij= λiδij, for all 1 ≤ i,j,k ≤ n where λj,k=ek(λj).It follows that for any 2≤i,j≤n and 1≤k≤n.From(4.64),we can see that By applying the similar discussion as in the proof of Theorem 4.1,we can see that M is locally a product of a part of the principal curvature line and a piece of the(n−1)-dimensional totally geodesic submanifold of Nn+1.This completes the proof of Theorem 4.2. AcknowledgementThe authors wish to make a grateful acknowledgement to the referees for their advice on the original manuscript. [1]Deshmukh,S.,Al-Odan,H.and Shaman,T.A.,Tangent bundle of the hypersurfaces in a Euclidean space,Acta.Math.Acad.Paedagog.Nyh´azi(N.S.),23(1),2007,71–87. [2]Klingenberg,W.and Sasaki,S.,On the tangent sphere bundle of a 2-sphere,Tohôku Math.J.,27,1975,49–56. [3]Konno,T.,Killing vector fields on tangent sphere bundles,Kodai Math.J.,21,1998,61–72. [4]Konno,T.and Tanno S.,Geodesics and Killing vector fields on the tangent sphere bundle,Nagoya Math.J.,151,1998,91–97. [5]Kowalski,O.,Curvature of the induced Riemannian metric of the tangent bundle of Riemannian manifold,J.Reine Angew.Math.,250,1971,124–129. [6]Miyaoka,R.,Complete hypersurfaces in the space form with three principal curvatures,Math.Z.,179,1982,345–354. [7]Munteanu,M.I.,Cheeger Gromoll type metrics on the tangent bundle,Sci.Ann.Univ.Agric.Sci.Vet.Med.,49(2),2006,257–268. [8]Munteanu,M.I.,Some aspects on the geometry of the tangent bundles and tangent shpere bundles of a Riemannian manifold,Mediterr.J.Math.,5,2008,43–59. [9]Musso,E.and Tricerri,F.,Riemannian metrics on tangent bundles,Ann.Math.Pura Appl.,150(4),1988,1–20. [10]Nagano,T.,Isometries on complex-product spaces,Tensor,New Series,9,1959,47–61. [11]Nagy,P.T.,On the tangent sphere bundle of a Riemannian 2-manifold,Tohôku Math.J.,29,1977,203–208. [12]Nagy,P.T.,Geodesics on the tangent sphere bundle of a Riemannian manifold,Geom.Dedicata.,7(2),1978,233–243. [13]Sasaki,S.,On the differential geometry of tangent bundles of Riemannian manifolds I,II,Tohôku Math.J.,10,1958,338–354;14,1962,146–155. [14]Sasaki,S.,Geodesics on the tangent sphere bundles over space forms,J.Reine Angew.Math.,288,1976,106–120. [15]Tachibana,S.and Okumura,M.,On the almost-complex structure of tangent bundles of Riemannian spaces,Tohôku Math.J.,14(2),1962,156–161. [16]Tashiro,Y.,On contact structure of hypersurfaces in complex manifolds I,II,Tohôku Math.J.,15,1963,62–78;167–175. [17]Tashiro,Y.,On contact structures of tangent sphere bundles,Tohôku Math.J.,21,1969,117–143.
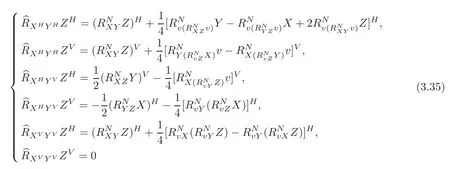

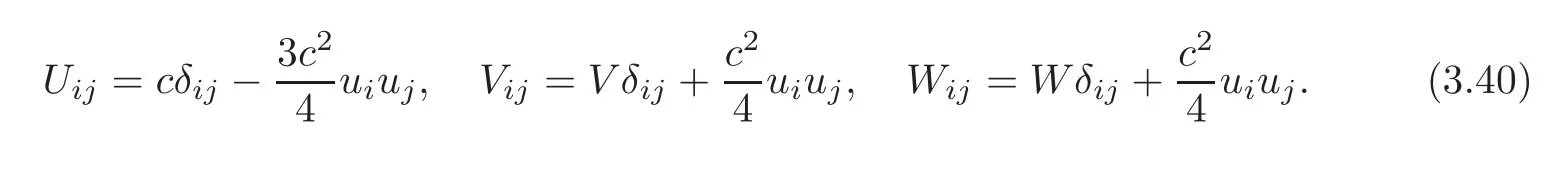
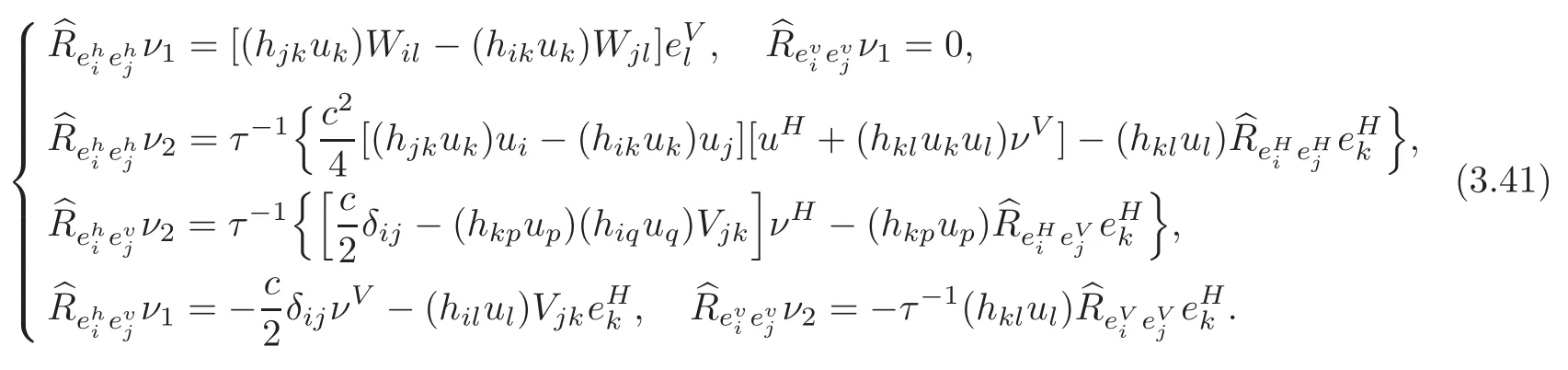
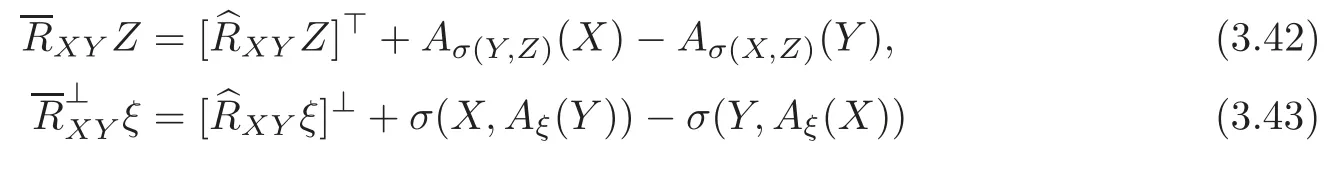
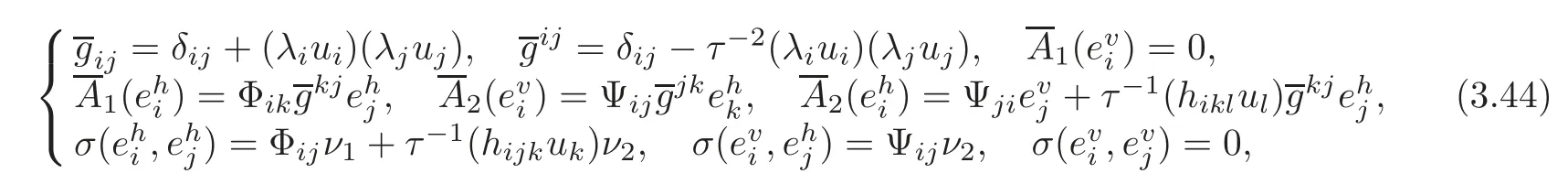
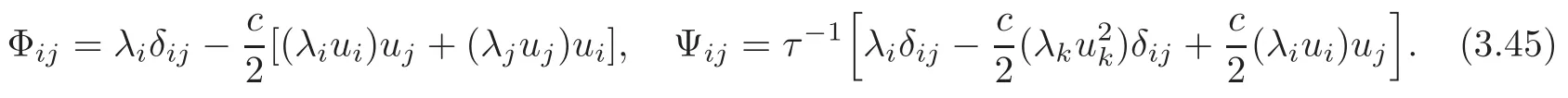
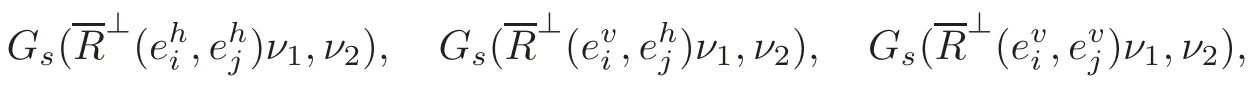
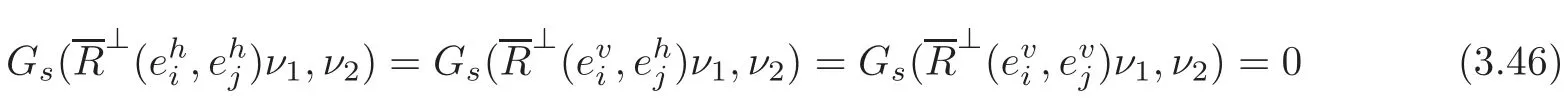
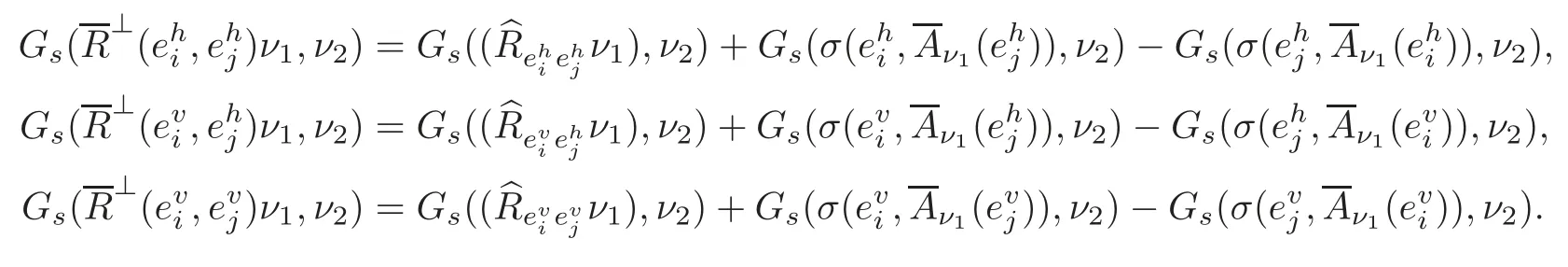
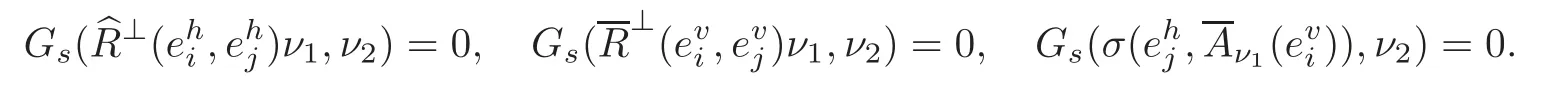
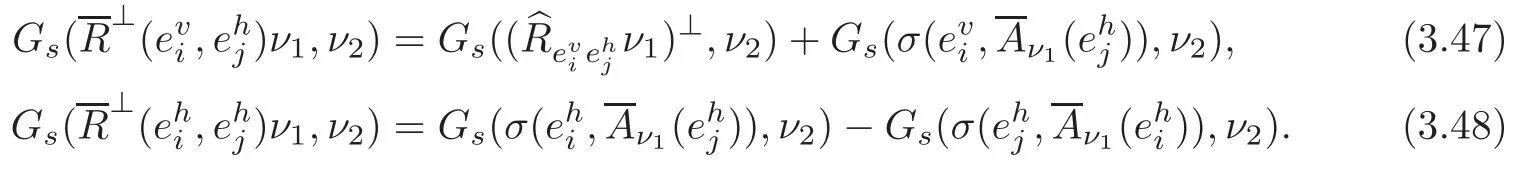

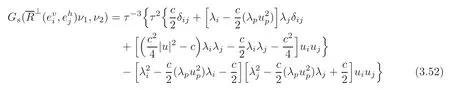
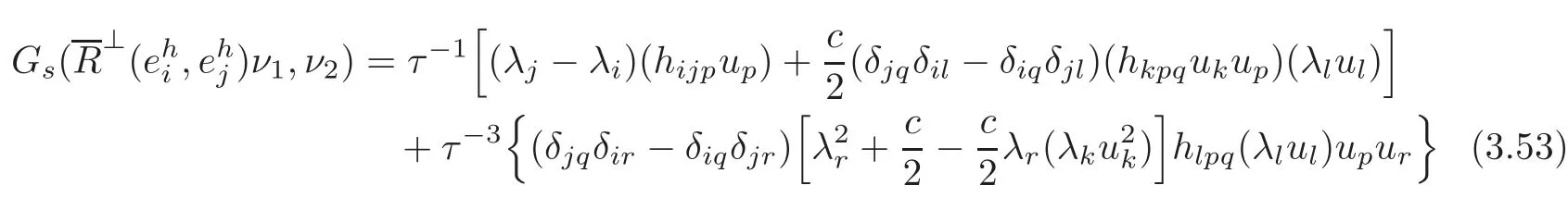
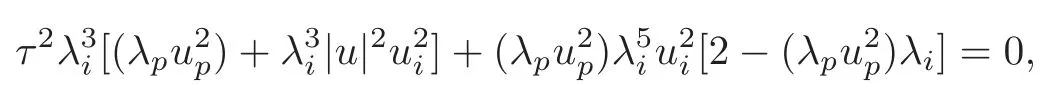
4 The Almost Complex Structure on TM
4.1 The induced almost complex structure on TM

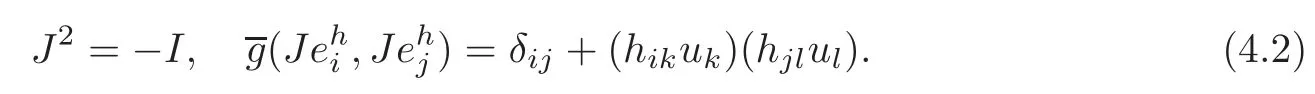
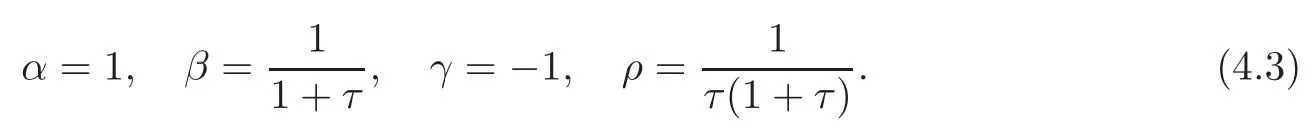
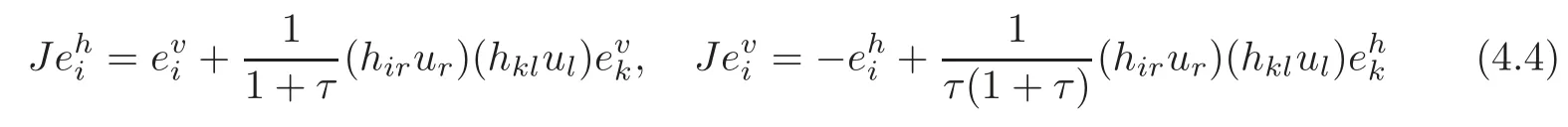
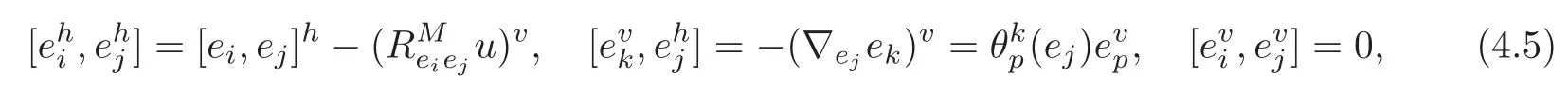
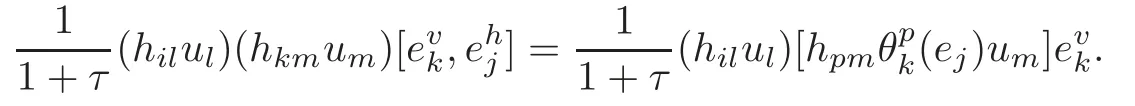

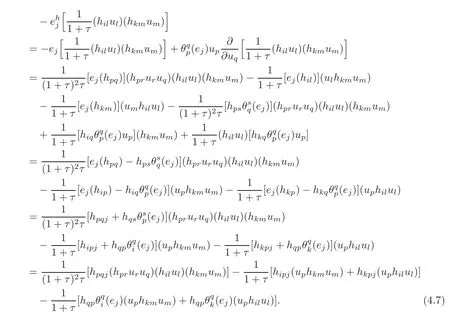

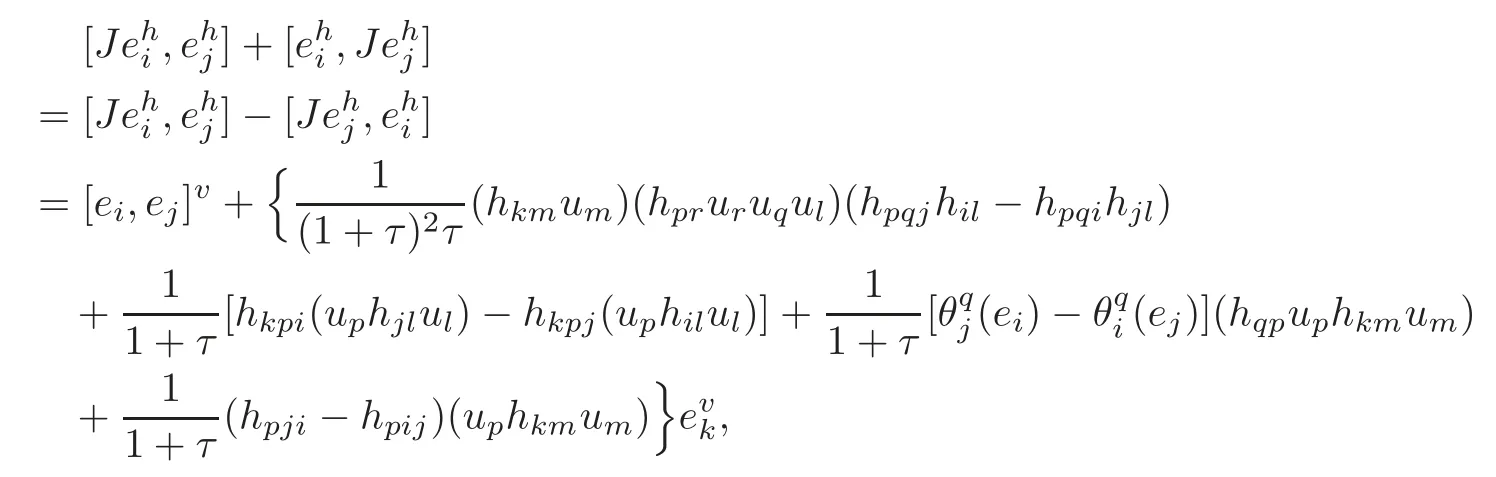
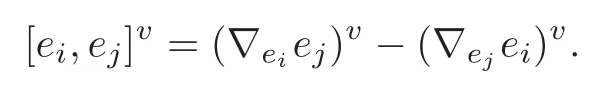

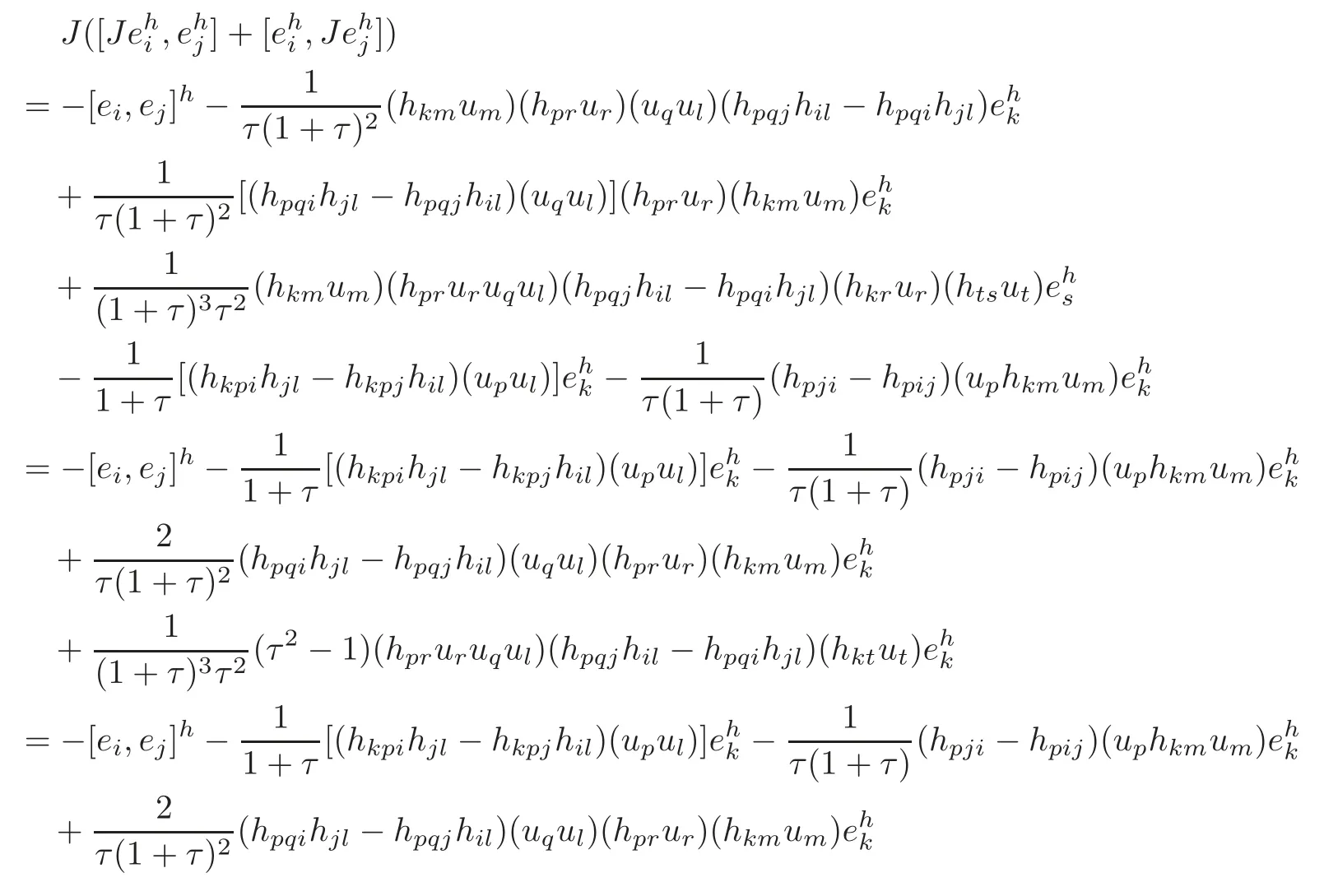
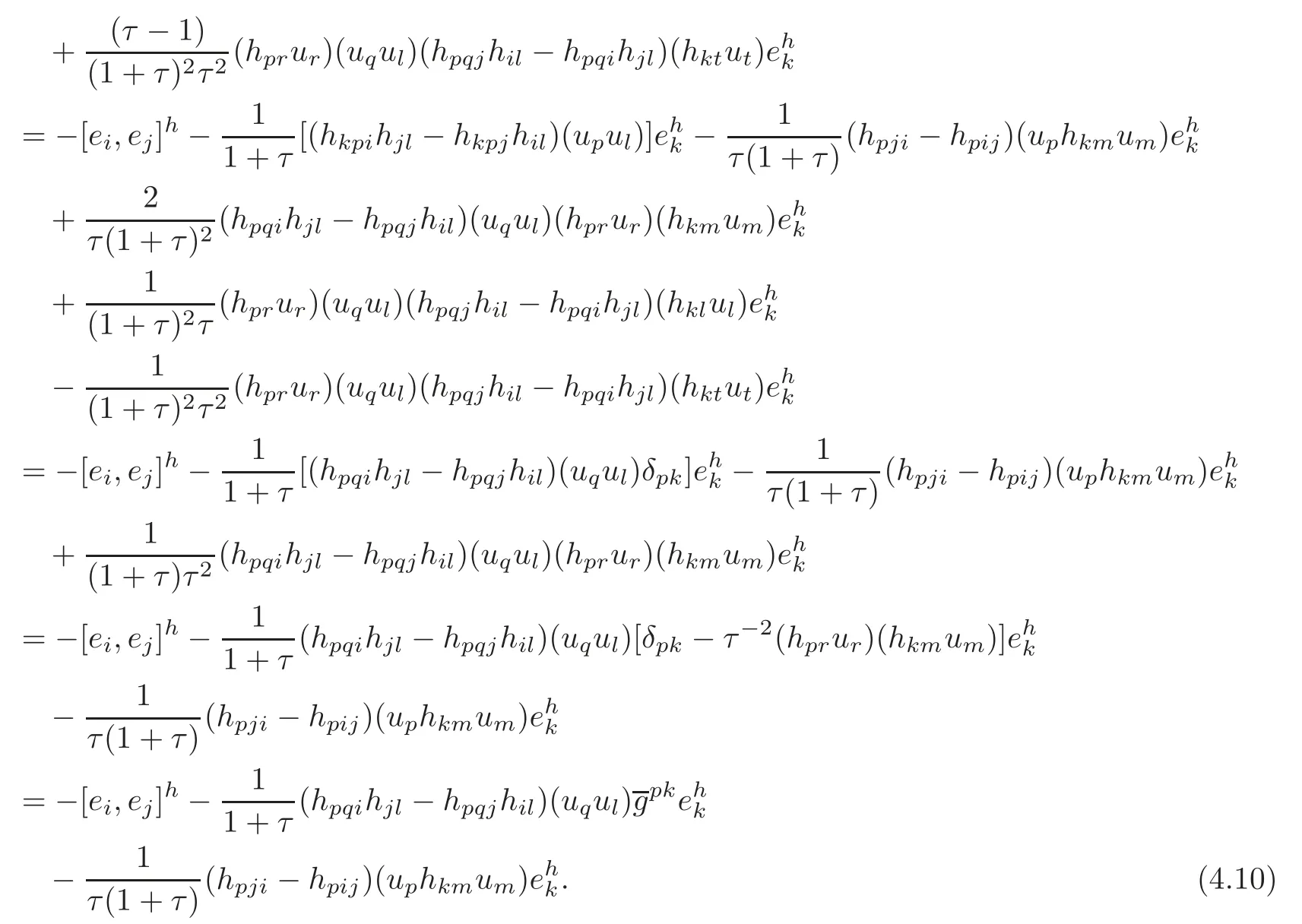
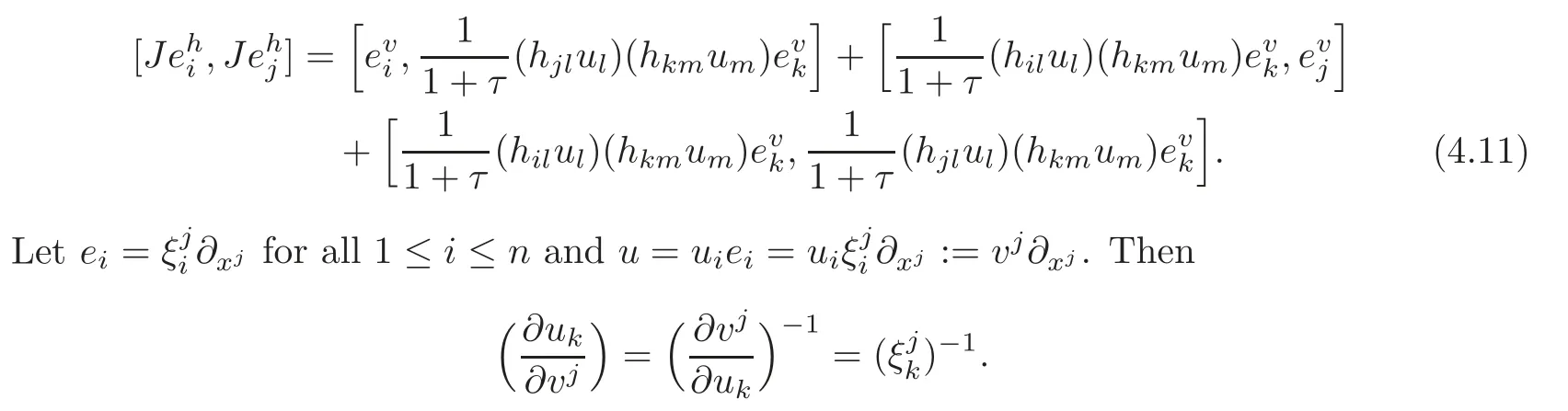
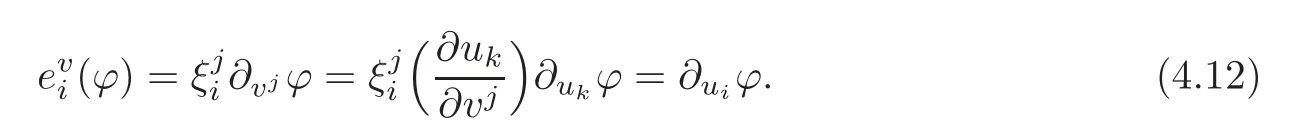

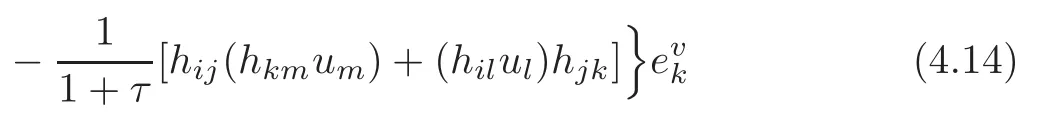
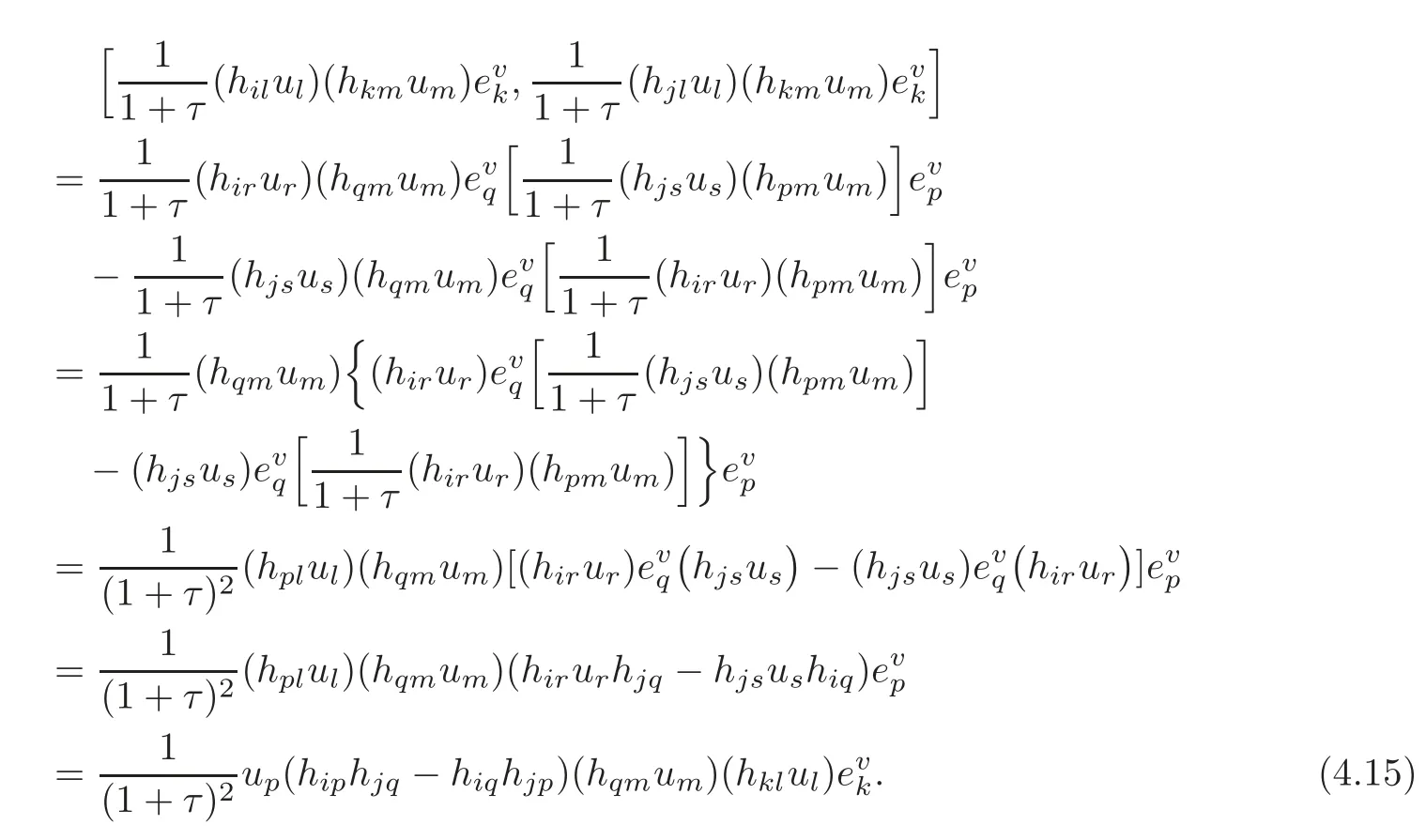
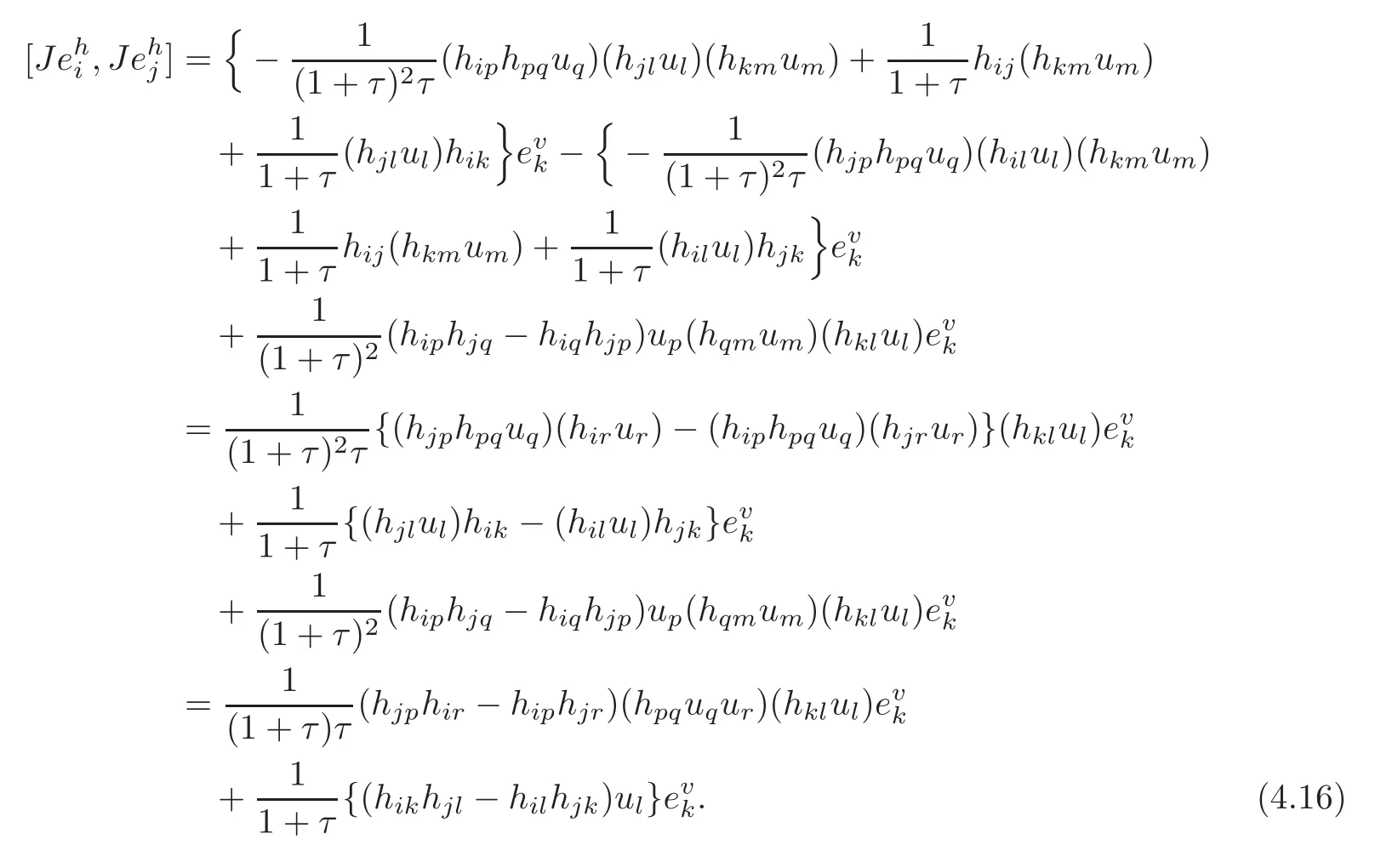



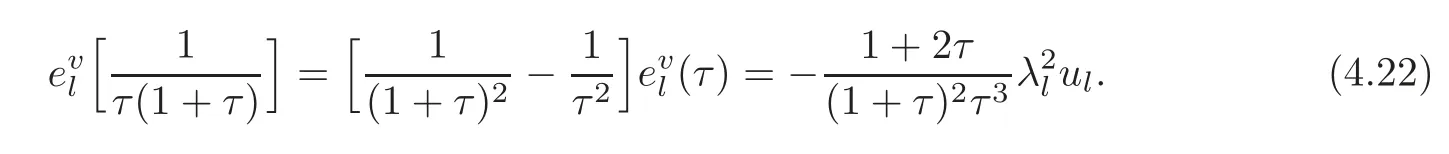

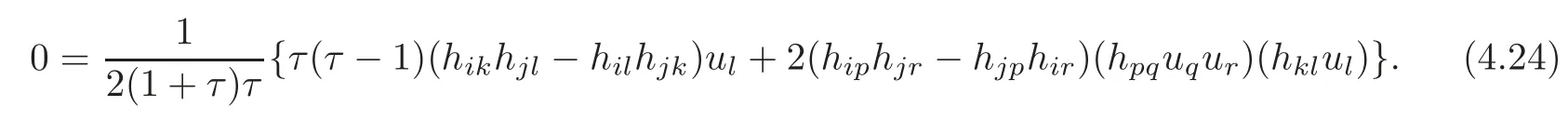
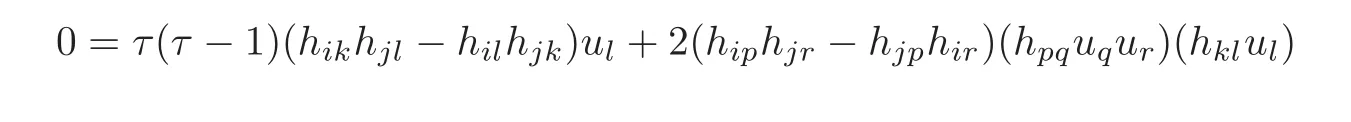
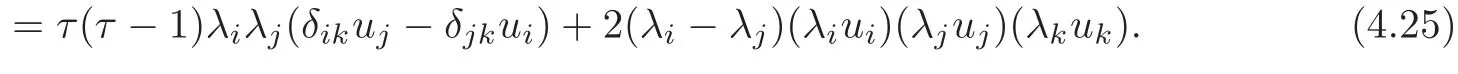
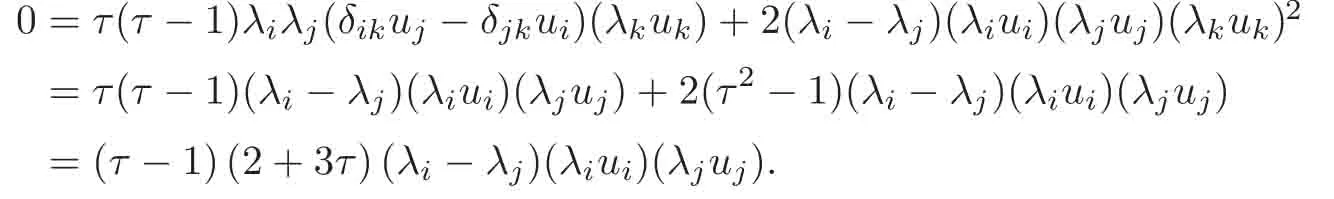



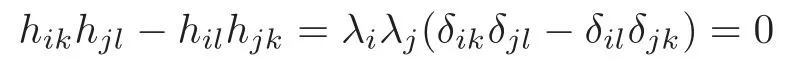

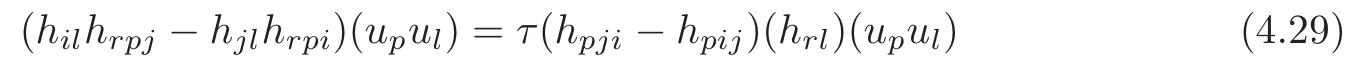
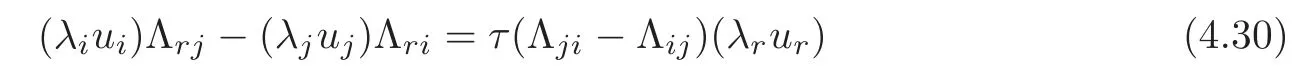
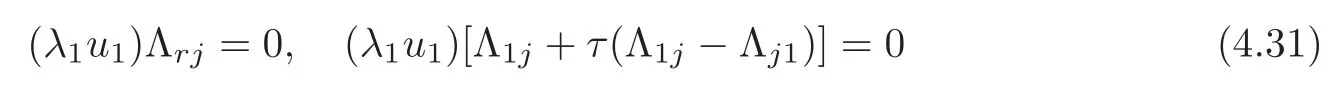

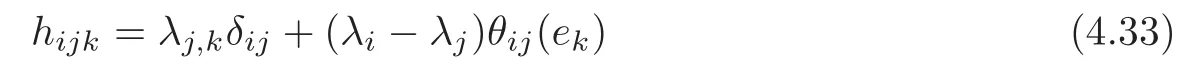



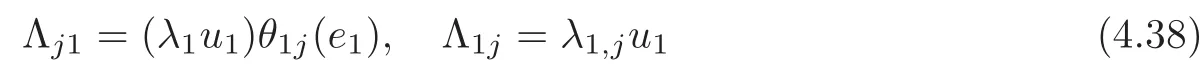



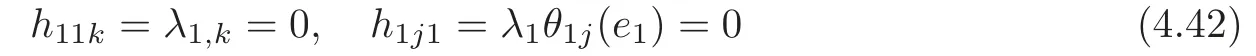
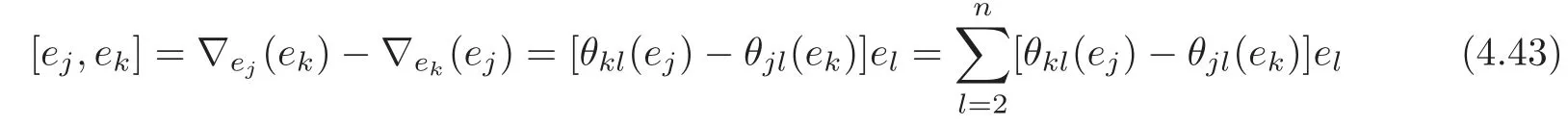
4.2 The induced Khlerian form on TM

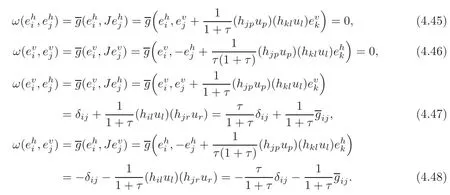
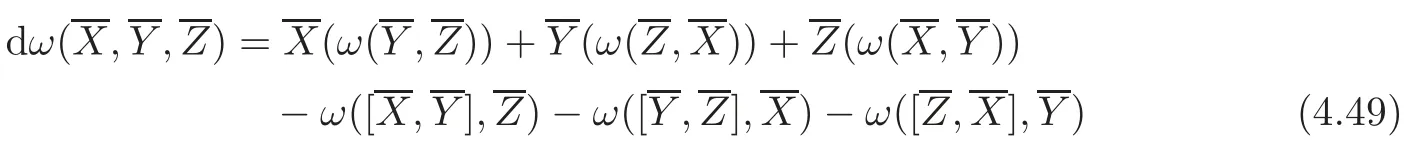
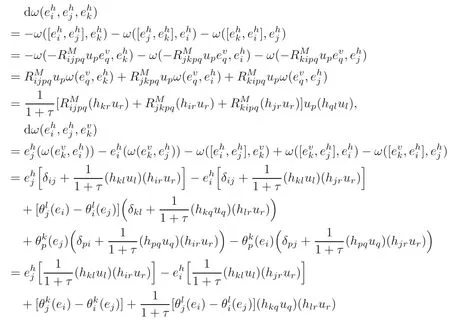

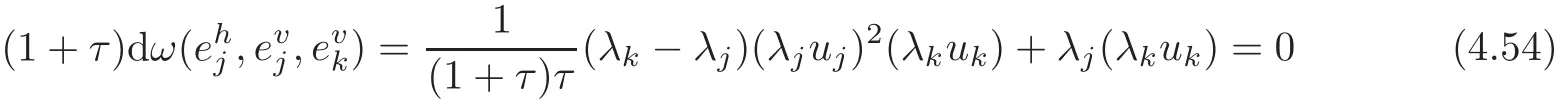

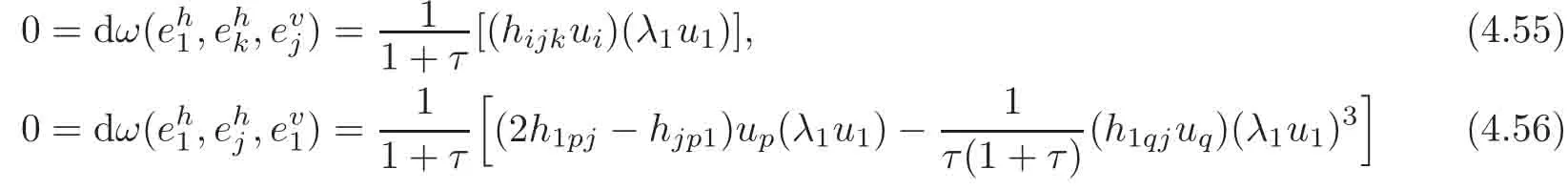

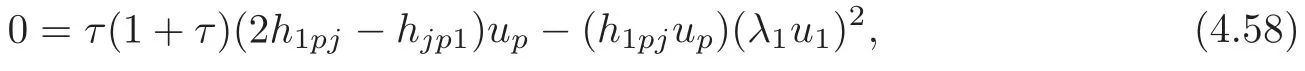

杂志排行
Chinese Annals of Mathematics,Series B的其它文章
- A Result on the Quasi-periodic Solutions of Forced Isochronous Oscillators at Resonance∗
- BSDEs with Jumps and Path-Dependent Parabolic Integro-Differential Equations∗
- Hochschild Cohomology Rings of Temperley-Lieb Algebras∗
- On the Dedekind Sums and Two-Term Exponential Sums∗
- Randomly Weighted LAD-Estimation for Partially Linear Errors-in-Variables Models
- On the Lie Algebras,Generalized Symmetries and Darboux Transformations of the Fifth-Order Evolution Equations in Shallow Water∗
