On the Lie Algebras,Generalized Symmetries and Darboux Transformations of the Fifth-Order Evolution Equations in Shallow Water∗

Shoufu TIAN Yufeng ZHANG Binlu FENG Hongqing ZHANG

1 Introduction

Group-theory methods are useful for finding symmetry reductions and corresponding groupinvariant solutions of a partial differential equations(PDEs)system(see[2,14,23]).The local theory of symmetries of differential equations has been well-established since the days of Sophus Lie.Generalized,or higher-order symmetries can be traced back to the original paper of Noether[22],and has acquired received added importance after the discovery that they play a critical role in integrable(soliton)partial differential equations(see[2,14,23]).While the local theory is very well developed,the theory of nonlocal symmetries of nonlocal differential equations remains incomplete.However,little importance is attached to the existence and applications of nonlocal symmetries[2–3,23].Recently,there is some outstanding literature on research of the generalized symmetries.Internal,external and generalized symmetries are investigated in[1].A loop algebra of nonlocal isovectors of the Korteweg-de Vries(KdV)equation is introduced in[10].By inverse recursion operators,in finitely many nonlocal symmetries and the conformal invariant forms(Schwartz forms)are researched in[6,20–21].Based on the geometric heat f l ows,symmetries,invariant solutions and reduced equations for the affine case are investigated in[11,19,25–26,38].ComplexPT-symmetric extensions of the non-PT-symmetric Burger’s equation are researched in[37].Furthermore,the introduction of potential-type symmetries(see[2])and pseudopotential-type symmetries(see[36])is proposed,which admits close prolongation extending the applicability of symmetry methods to obtain analytic solutions of evolution equations.In that context,the original given system can be embedded in some prolonged systems.Hence,these nonlocal symmetries with close prolongation are anticipated in[9,27].

Recently,together with Bluman et al.,we use the nonclassical method to construct“nonclassical symmetries”and time-dependent exact solutions for the dimensional nonlinear Kompaneets equation(see[4]).Interestingly,each of these solutions is expressed in terms of elementary functions.Three of the classes exhibit quiescent behavior,and the other two classes exhibit blow-up behavior in finite time.As a consequence,it is shown that the corresponding nontrivial stationary solutions are unstable.By virtue of the Riemann theta function,we obtain some periodic wave solutions of nonlinear evolution equations,discrete evolution equations and supersymmetric evolution equations(see[12,29–33]).In particular,we investigate the integrability of a generalized variable-coefficient Kadomtsev-Petviashvili equation and a forced Kortewegde Vries equation in fluids(see[34–35]),respectively.In this paper,we present a method to research generalized symmetries and their applications of a generalized fifth-order evolution equation by virtue of some new pseudo-potential systems.The method is applied to obtain the generalized symmetries of a generalized fifth-order Korteweg-de Vries equation,named the OWW equation.As applications of the symmetries,we further investigate Lie algebras,initial value problems and Darboux transformations of these fifth-order evolution equations.

In 1984,Olver[24]derived a one-dimensional model for describing long,small amplitude waves in shallow water.The model can take the wave velocity or,alternatively,the surface elevation as the principal variable.Exact solutions for the first case were obtained in the work[17].The second case leads to the equation

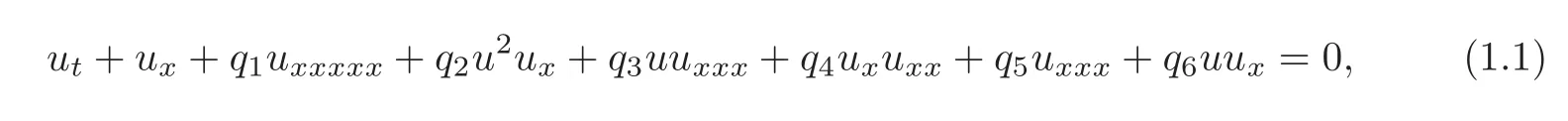
whereu=u(x,t)provides a surface elevation,xis the horizontal coordinate,and real constantsqi(i=1,···,6)depend on the surface tension,which are given by

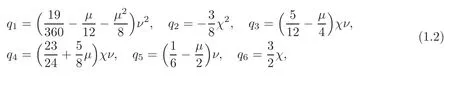
whereμdenotes a dimensionless surface tension coefficient,νis the square of the ratio of fluid depth to wave length,andχis the ratio of wave amplitude to undisturbed fluid depth.The small parametersνandχare assumed to be the same order of smallness.For no surface tension,all these coefficients are nonzero,otherwise some of them can be taken as zero values.

The purpose of this paper is to present the method of obtaining generalized symmetries,Lie algebras,initial value problems and Darboux transformations.Taking the well-known fifthorder evolution equation,the OWW equation(1.1),as a special example,we present some structures associated with the Olver water wave(AOWW)equations,such as a Lie algebra of the generalized symmetries,which consider some new smooth functions:and a restriction:Moreover,the generalized symmetries are applied to investigate initial value problems and Darboux transformations.The results are also extended to AOWW equations,such as Lax,Sawada-Kotera,Kaup-Kupershmidt,Itô and Caudrey-Dodd-Gibbon-Sawada-Kotera equations,et al.

The rest of the paper is organized as follows.In Section 2,for nonlinear partial differential equations,we propose a detailed description of the method to construct the generalized symmetries by considering the nonlocal condition.By virtue of the method,in Section 3,we introduce the corresponding pseudo-potential systems to obtain some generalized symmetries and Lie algebras of the OWW and AOWW equations,respectively.In Section 4,we present some applications for the generalized symmetries,such as initial value problems and Darboux transformations.Finally,conclusions and discussions are presented in Section 5.

2 Generalized Symmetries of Partial Differential Equations

In this section,based on[1–28],we mainly present a detailed description of the method to construct the generalized symmetries by considering the nonlocal condition.

Notational conventionsThroughout this paper,we suppose the following notations.Independent variables are denoted byxi,i=1,2,···,n,x=(x1,x2,···,xn),and dependent variables are denoted byuα,α=1,2,···,m,u=(u1,u2,···,um).Partial derivatives with respect toxiare indicated by sub-indices,andDiimplies the total derivatives with respect to some independent variablexi,

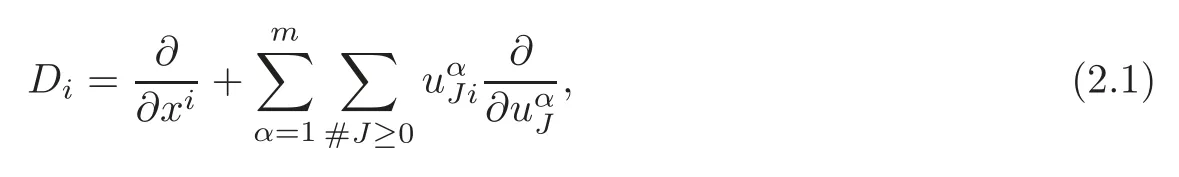
where the unorderedk-tupleJ=(j1,j2,···,jk),0≤j1,j2,···,jk≤nstands for a multi-index of order#J=k,andDJimplies the compositionDJ=Dj1Dj2···Djk.

Definition 2.1Suppose that N is a non-zero integer.An N-dimensional covering π of a system of partial differential equation(s)△σ[x,u]=0,σ=1,2,···,k,is a triplet

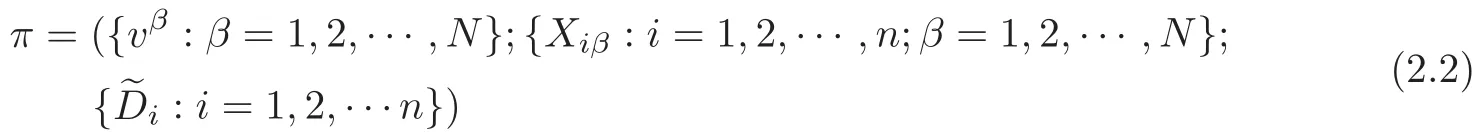
of variables vβ:v=(v1,v2,···,vN),where smooth functions Xiβdepend on xi,uα,vβand afinite number of partial derivatives ofuα,vβ,and linear operators

satisfy the following system:

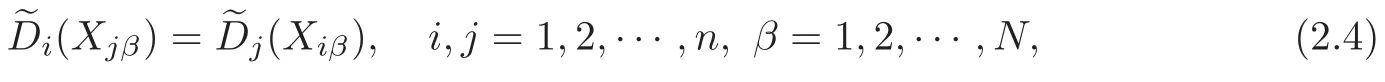
wheneveruα(xi)is a solution of

As we understand hereafter that the index i runs from 1 to n and that the index β runs from 1 to N,we replace(2.2)by writing π =(vβ;Xiβ;i).The variables vβare considered as new dependent variables(the “nonlocal variables” of the theory)and the operatorsisatisfying system(2.4)are new total derivatives which are used to consider the nonlocal variables vβ.Interestingly,the operatorsisatisfy

and these equations are compatible because the system(2.4)holds.Owing to the solutions o f systemthe total derivativesibecome ordinary partial derivatives.The system

holds for each index β and each index i whenever uα(xi)is a solution ofThese compatible equations specify the relations between the dependent variables uαand the nonlocal variables vβ.

The nonlocal version of the formal linearization of the systemis the matrix

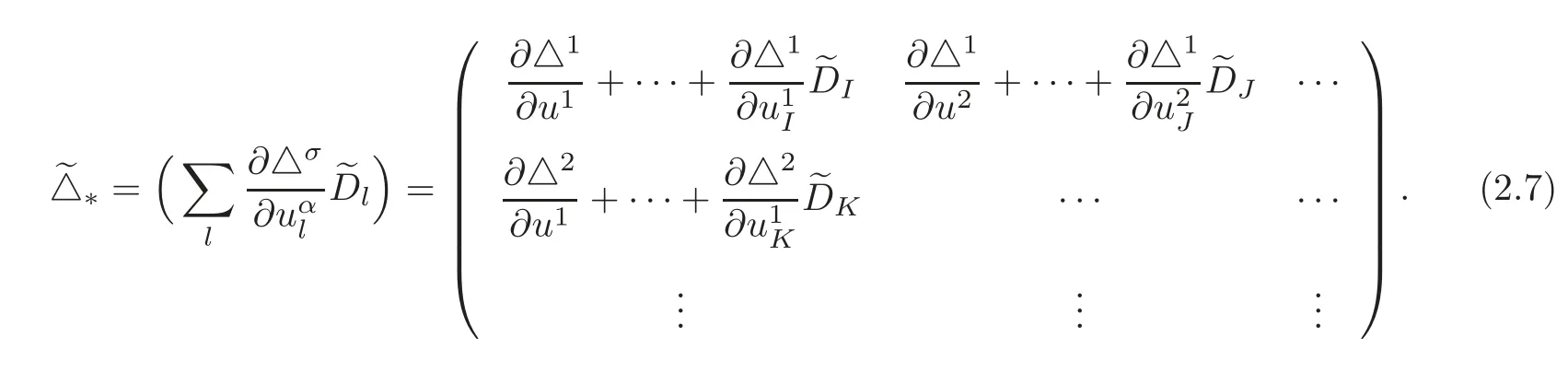
The following is our definition of nonlocal symmetries by considering the nonlocal condition.

De finition 2.2Suppose thatσ =1,2,···,k,is a system of differentialequations,and assume thatis a covering ofA nonlocalπ-symmetry ofgiven by a generalized vector field

of the augmented system

is a nonlocal symmetry if and only if X satisfies

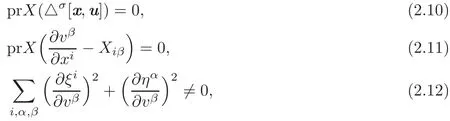
where prX is given by

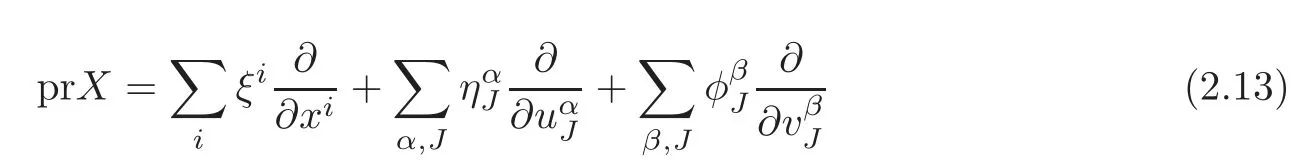
and

Otherwise,X is a local symmetry of the system △σ[x,u]=0.

Now,in order to capture all possible generalized symmetries of the augmented system(2.9),as explained in[23],it is enough to consider evolutionary generalized vector fields.Thus,hereafter we shall only consider the generalized vector field X of the form

where Gαand Hβare smooth differential functions.As we know,in this case the generalized symmetry conditions(2.10)and(2.11)imply that the in finitesimal deformation uαuα+εGαsatisfies the system △σ[x,u]=0 with first order for the deformation parameter ε,and that the in finitesimal deformation vβvβ+ εHβsatisfies the compatible system(2.9)with first order for ε.Then we have the following proposition.

Proposition 2.1Suppose that △σ[x,u]=0,σ =1,2,···,k,is a system of partial differential equations,and assume that π =(vβ;Xiβ;i)is a covering of △σ[x,u]=0.A nonlocal π-symmetry of △σ[x,u]=0 is a generalized vector field generated by an ordered(m+N)-tuple of functions(Gα,Hβ)depending on xi,uα,vβand a finite number of xi-derivatives of u,vβ

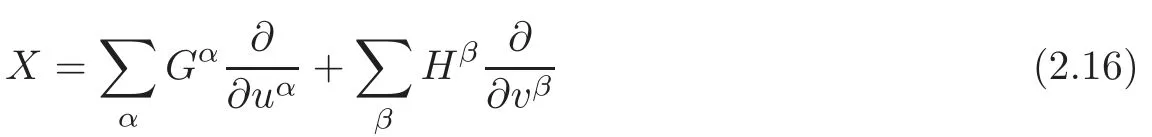
of the augmented system

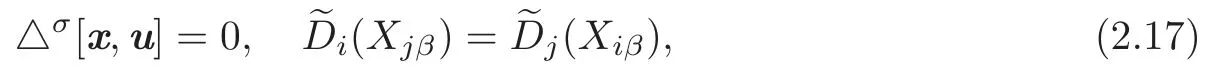
where Gαand Hβare differential functions,and

if and only if X satisfies

whenever uα(xi)is a solution of △σ[x,u]=0,where the operatorεappearing in(2.20)is given by

Otherwise,X is a local symmetry of the system △σ[x,u]=0.

It is worth emphasizing that(2.19)depends only on the vector G and the system △σ[x,u].From the view point of Krasil’shchik and Vinogradov[36],one can see that the vector G is the π-shadow of the nonlocal π-symmetry(Gα,Hβ).Also important to note is that the differential operatorεdefined in(2.22)is the nonlocal version of the in finite prolongation of the vector field

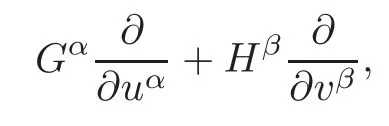
by considering the fact that the derivatives of the new nonlocal variables vβcan be written in terms of the variables xi,uα,,vβand

We always call“nonlocal symmetry” instead of“nonlocal π-symmetry”,and suppose that a covering(2.2)of the system △σ[x,u]=0 has been fixed.The fact that this method of nonlocal symmetries depends essentially on coverings indicates that one should perhaps consider nonlocal symmetries to be properly generalizing the class of intrinsic symmetries studied in[1].

Proposition 2.2Let(Gα,Hβ)be a nonlocal π-symmetry of the system △σ[x,u]=0,where the covering π is given by(2.2),and then the vector field

is a generalized symmetry of the augmented system(2.9).That is to say,if(Gα,Hβ)is a nonlocal π-symmetry of the system △σ[x,u]=0,the linearized system

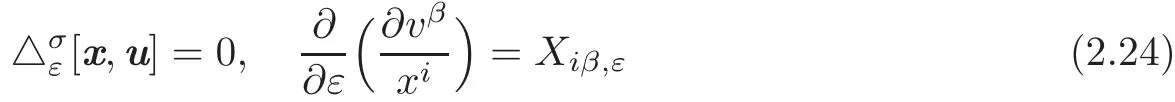
is satis fied withwhenever uα(xi)and vβ(xi)satisfy the augmented system(2.9).On the other hand,if the vector field(2.23)is a generalized symmetry of the augmented system(2.9),then(Gα,Hβ)is a nonlocal π-symmetry of △σ[x,u]=0,where π =(vβ;Xiβ;i)and

Because the generalized symmetry transforms a solution into another solution(see[23]),Proposition 2.2 indicates the following corollary.

Corollary 2.1Letandbe solutions of the augmented system(2.9),and the solution of the Cauchy problem

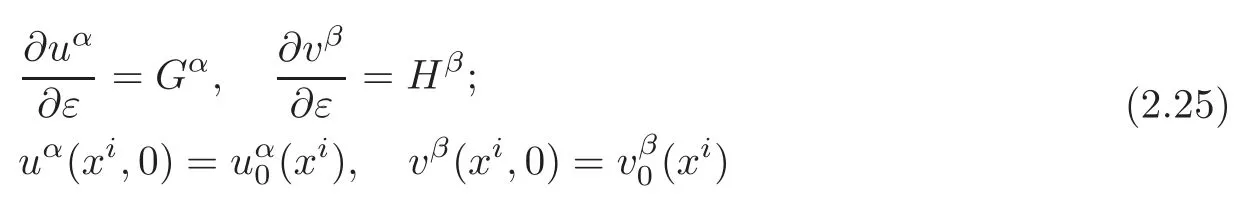
is a one-parameter family of solutions to the augmented system(2.9).In particular,nonlocal symmetries transform solutions of the system △σ[x,u]=0 to solutions for the same one.

We end this section by providing some examples.

Example 2.1A nonlinear telegraph(NLT)system reads

The functions

where X1=x−u2,X2=t−logu1,and f1,f2satisfy the following linear PDE system:

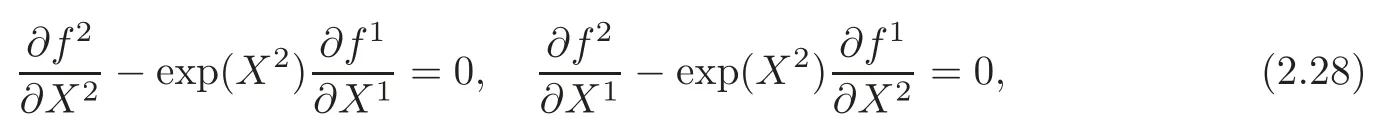
which admit the following condition:Let u1,u2be solutions of the NLT system(2.26),and the“deformation” u+ εη with x+ εξ1,t+ εξ2is also a solution of the first order in parameter ε,namely,the functions ξ1,ξ2and η satisfy the linearized NLT equation.On the other hand,in order to make this observation rigorous,we should take into account an extra nonlocal variable v1by satisfying

Therefore,the function η in(2.27)can be rewritten as η=exp(−t),and then η is a “local” and could perhaps be considered as the characteristic of a local symmetry for the following augmented system:

Example 2.2The Burger’s equation reads

The function

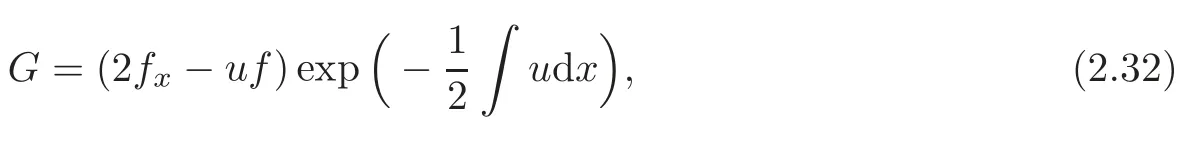
where f=f(x,t)satisfying ft−fxx=0,admits the following condition:Let u be a solution of the Burger’s equation(2.31),the “deformation” u+ εG is also a solution of the first order in parameter ε,namely,the function G satisfies the linearized Burger’s equation.On the other hand,in order to make this observation rigorous,we would take into account an extra nonloal variable v1by satisfying

Therefore,the function(2.32)can be rewritten asand then G is a “local” and could perhaps be considered as the characteristic of a local symmetry for the following augmented system:

Remark 2.1In Example 2.1,setting x1=x and x2=t,one has N=1,X11=u2,X21=u2,and the first two equations of(2.30)correspond to the system(2.6).Similarly,in Example 2.2,setting x1=x and x2=t,one has N=1,X11=u,and X21=ux+12u2,and the last two equations of(2.34)correspond to the system(2.6).

Remark 2.2Since we are allowed to replace all derivatives of vβappearing in the equation(2.16)by virtue of system(2.6),it is worth emphasizing that the coefficients Gαand Hβof the vector field(2.16)are supposed to depend not only on xi,uα, finite numbers of derivatives of uα,and the new variables vβ,but also finite numbers of derivatives of vβ.This simpli fication is crucial to obtain the classi fication results.

3 Lie Algebras and Generalized Symmetries of the OWW and AOWW Equations

Let’s begin this part with some classical reductions of physical and mechanical interests,recent examples of the OWW equation(1.1),among others,include the following:

(1)The Lax equation reads(see[18])

(2)The integrable Sawada-Kotera(SK)equation reads(see[29])

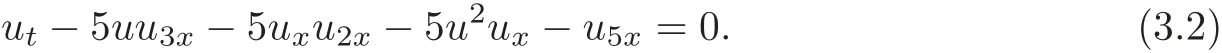
(3)The Kaup-Kupershmidt(KK)equation reads(see[15–16])

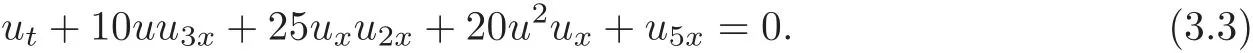
(4)The Itô equation reads(see[13])

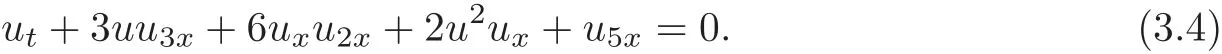
(5)The Caudrey-Dodd-Gibbon-Sawada-Kotera equation(CDGSK)reads(see[7–8,29–30])

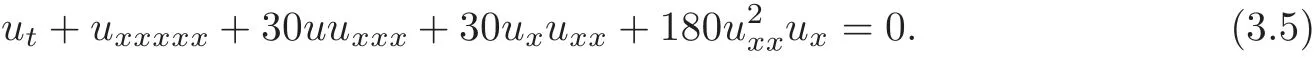
In what follows,we investigate some pseudo-potentials,generalized symmetries and Lie algebras for the OWW and AOWW equations,respectively.

Theorem 3.1The system of equations

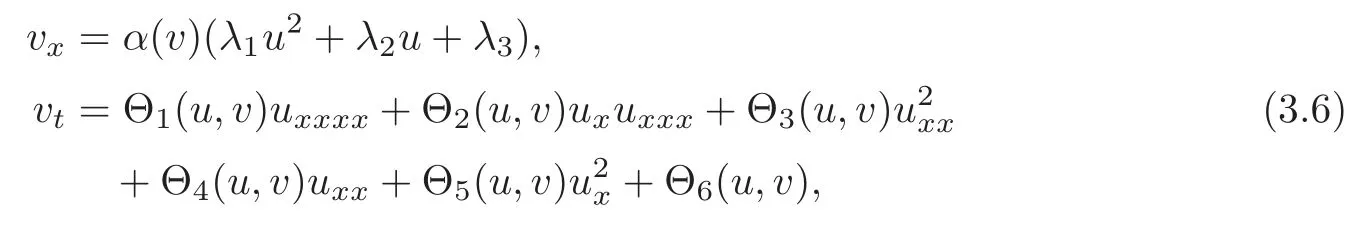
with

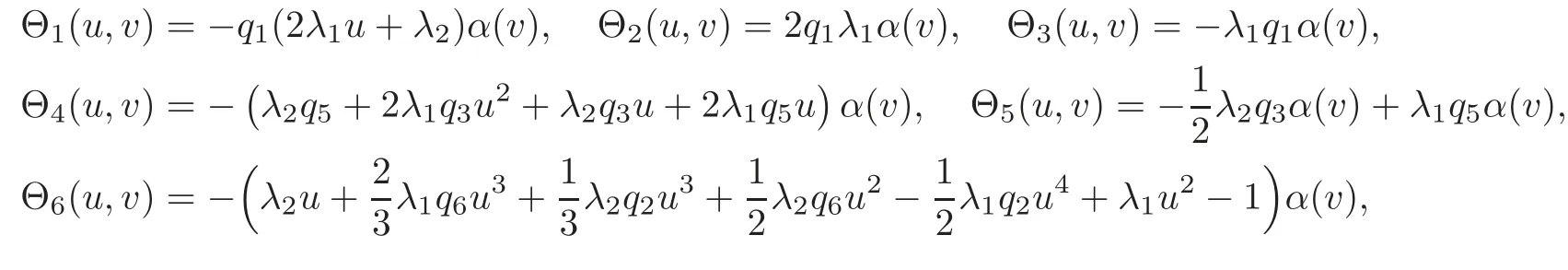
is completely integrable on solutions to the OWW equation for q4=2q3,where λ1,λ2,λ3are some nonzero real parameters and α(v)is an arbitrary function of v.Hence it determines a pseudo-potential v for the OWW equation.On the other hand,the following system of equations are compatible whenever u(x,t)is a solution of the OWW equation(1.1)and hence another potential w for(nonlocal)conservation laws of the OWW equation:

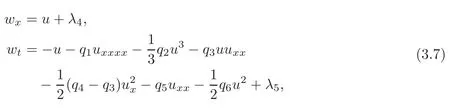
where λ4and λ5are also nonzero real parameters.

According to the idea of[5],the pseudo-potential v can be understood geometrically in terms of geodesics of the pseudo-spherical surfaces associated with the OWW equation(1.1).It is important to us that the compatible system of systems(3.6)–(3.7)yields a three-dimensional covering π of the Olver water wave equation with nonlocal variables v and w.

Remark 3.1By taking α(v)=here vi(i=1,2,···,n)are arbitrary constants.Theorem 3.1 is the“Riccati form”of the linear problem associated with the OWW equation(1.1)(see the classical paper by Chern et al[5]).

In what follows,we classify all first-order nonlocal π-symmetries of the OWW equation(1.1).In order to do this,one can see that it is necessary to assume that the parameter λiappearing in the systems(3.6)–(3.7)is also a ff ected by the symmetry transformation.Namely,the augmented system includes(1.1),(3.6)–(3.7)with the parameter λi.

The evolutionary vector field is of the form

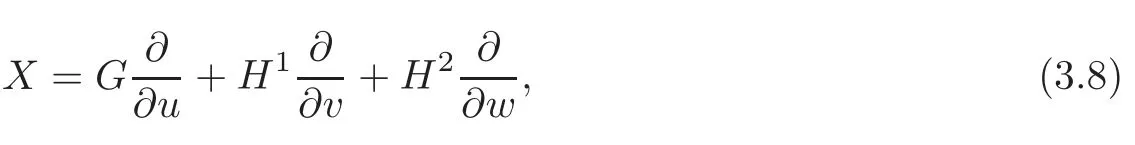
where G,H1and H2are functions of x,t,u,v,w,λiand the derivatives of u,v and w.

Theorem 3.2The first-order generalized symmetries of the augmented Olver water wave(AOWW)systems(1.1),(3.6)and(3.7),represented by vector fields(3.8),are linear combina-tions of

where β(v)=(λ2q5− 2λ3q3)α(v).Consequently,the vector field X9is a nonlocal π-symmetry of the OWW equation.

It is remarkable that the function β(v)is included in X9since it a ff ects the way in which λ varies with the in finitesimal symmetry transformation(3.17).This function is also of importance to our observations on the Lie algebra structure of nonlocal π-symmetries;see Corollary 3.1 below.We also note that X1and X2are simply the generators of shifts with respect to the independent variables:They are equivalent toandfor the OWW equation,respectively.

Corollary 3.1The nine symmetries(3.9)–(3.17)of the OWW equation generate a Lie algebra with the commutation Table 3.1,whenever u,v and w satisfy the augmented OWW system including(1.1),(3.6)and(3.7).

Table 3.1 The commutation table of the symmetry algebra for the OWW equationwith X0=X2−X1and X△=X0−qX4.

Table 3.1 The commutation table of the symmetry algebra for the OWW equationwith X0=X2−X1and X△=X0−qX4.

X1 X2 X3 X4 X5 X6 X7 X8 X9 X1 q3X1 q3X1 2q2q3X1 −q3X1 X2 q3X2 q3X2 2q2q3X2 −q3X2 X3 q3X3 2q2q3X3 X4 q3X4 q3X4 2q2q3X4 −q3X4 X5 −q3X1 −q3X2 −q3X4 52q33X4 −q23X0 X6 q3X6 2q2q3X6 −q33X4 X7 −q3X1 −q3X2 −q3X3 −q3X4 −52q33X4 −q3X6 −5q2q3X6 X?X8−2q2q3X1−2q2q3X2−2q2q3X3−2q2q3X4 −2q2q3X65q2q3X6 2q2q23X0 X9 q3X1 q3X2 q3X4 −q23X0 q33X4 −X? −2q2q23X0

Corollary 3.1 implies that the symmetries(3.9)–(3.17)generate a nine-dimensional Lie algebra G9.We stress the fact that this Lie algebra exists because we work on a fixed covering of the OWW equation:we cannot expect the “space of all nonlocal symmetries” of a given equation to possess a Lie algebra structure(see[36]).

It is worth emphasizing that the results of Theorems 3.1–3.2 and Corollary 3.1 depend on the condition q4=2q3.In what follows,replacing the condition by q3=q4,we consider the pseudo-potentials and nonlocal π-symmetries AOWW equations by taking the SK equation(3.2)for example,the results of which are quite di ff erent from those of Theorem 3.1 since the condition is changed.

We can obtain the following conclusions analogous to those obtained for the OWW equation.

Theorem 3.3The SK(AOWW)equation admits a pseudo-potential v determined by the compatible equations

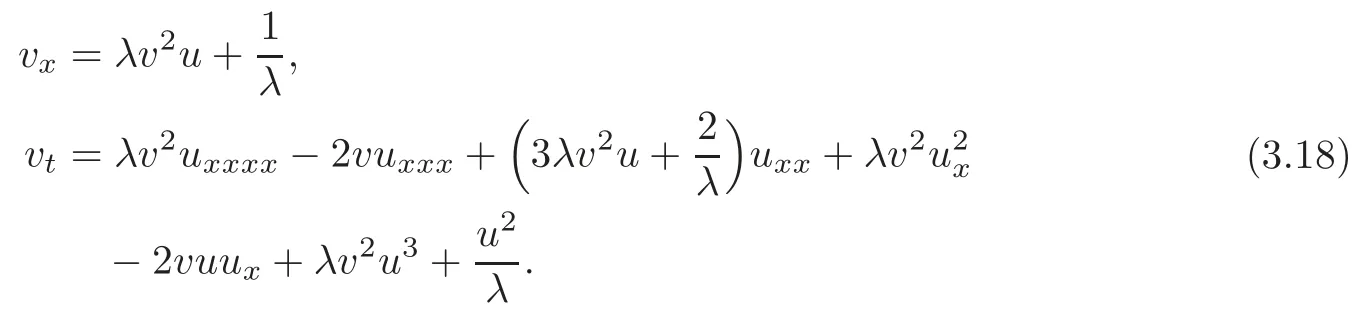
Moreover,the SK equation admits a potential w determined by the following two systems of equations,which are compatible whenever u(x,t)satisfies(3.2):

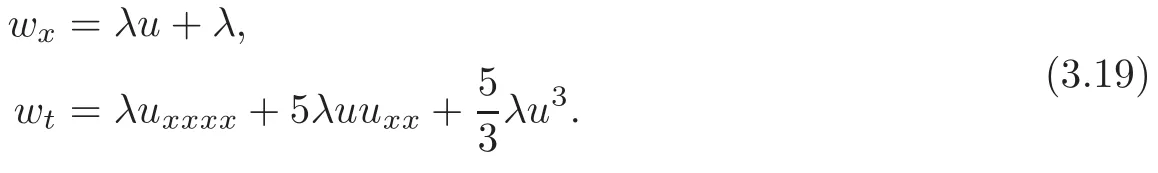
Theorem 3.4The first-order generalized symmetries of the augmented associated SK system(3.2),(3.18)and(3.19),represented by vector fields(3.8),with G,H1and H2being functions of the variables u,v,w,and the derivatives of u,v and w only,are linear combinations of

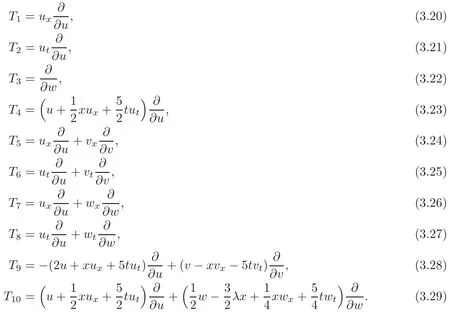
Corollary 3.2The ten symmetries(3.20)–(3.29)of the SK equation generate a Lie algebra with the commutation Table 3.2,whenever u,v and w satisfy the augmented SK systems(3.2),(3.18)and(3.19).

Table 3.2 The commutation table of the symmetry algebra for the SK equation.

4 Applications:The Finite Symmetry Transformation and Darboux Transformation

In this section,by virtue of the flow of the vector fields obtained in Theorems 3.2 and 3.4,we use our analysis to obtain explicit solutions to the OWW and AOWW(SK)equations.By using the standard theory of generalized symmetries(see[1,3,14,23–24]),we obtain a system of equations for the flow of the vector fields obtained in Theorem 3.2 and given by

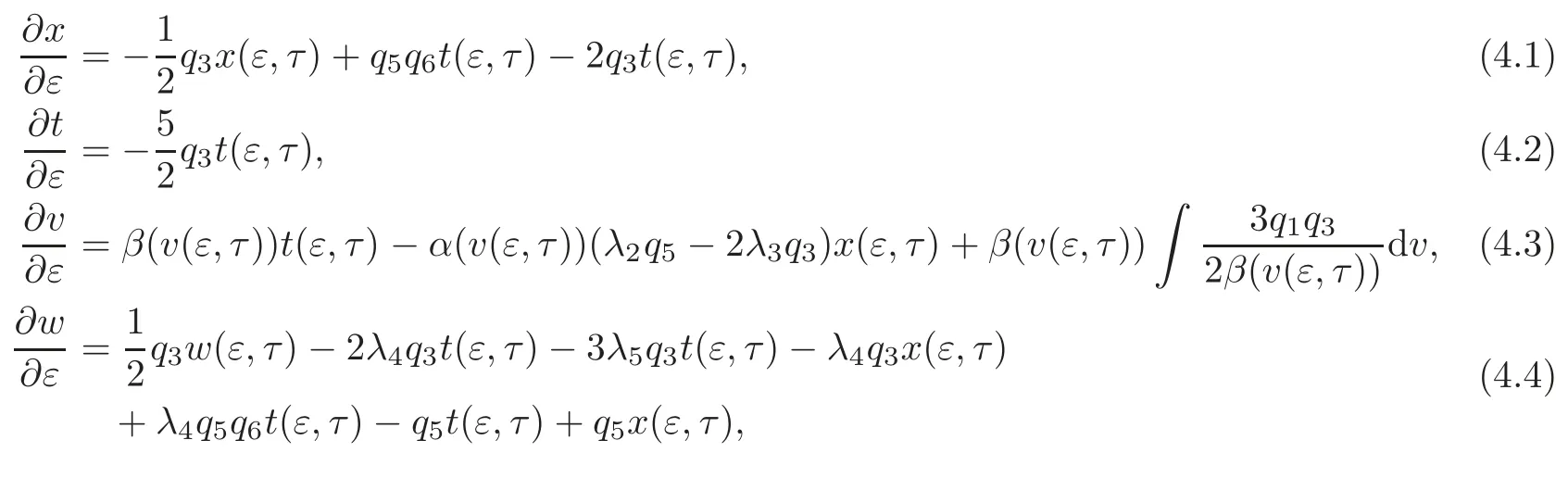
where ε denotes a flow parameter.There is no need to take into account an equation for u(ε,τ)since it is proven that actually u(ε,τ)is determined by the equations(4.1)–(4.4).

Proposition 4.1The initial value problem(4.1)–(4.4)with initial conditions

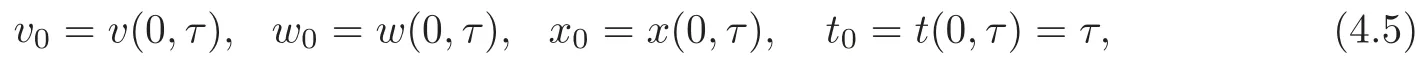
admits the following solution:

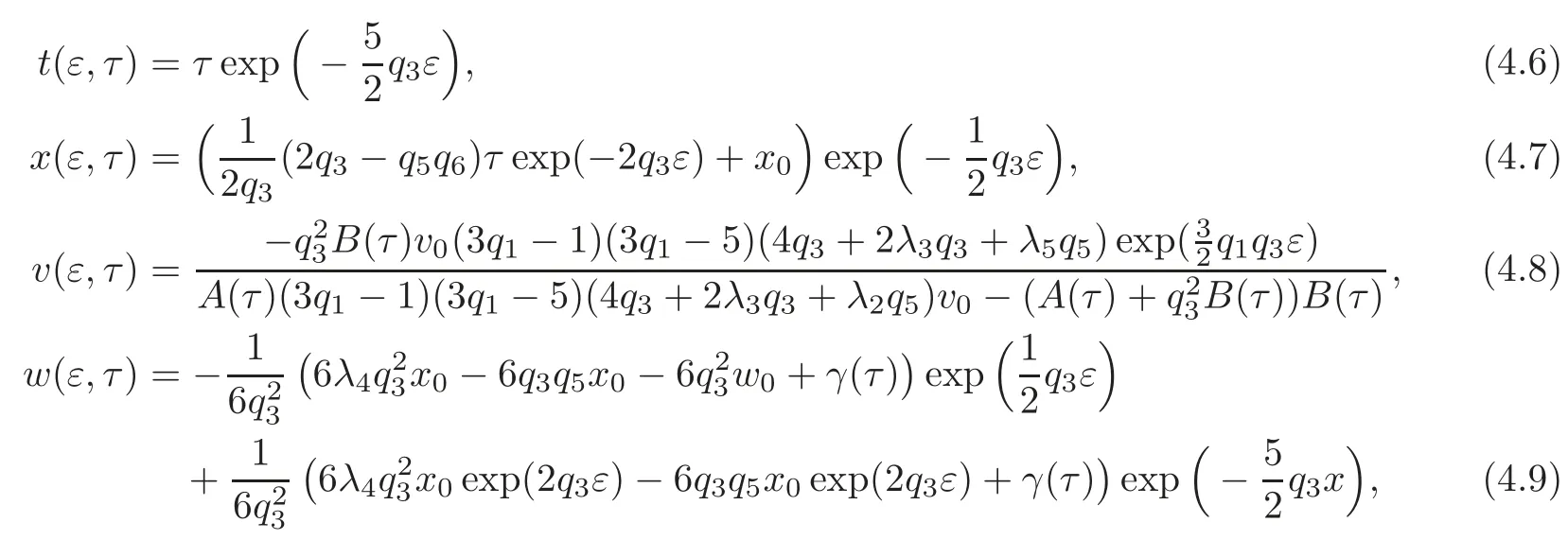
by taking α(v)=where γ(τ)is given by

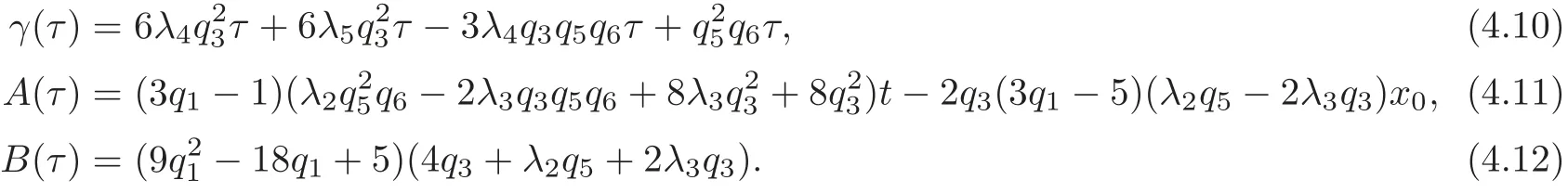
From this proposition,one can construct explicit families of solutions to the interesting OWW equation.In fact,it includes a Darboux transformation.Let us assume that the “old”independent variables are τ and t,and we can obtain the following results.

Theorem 4.1Suppose that the OWW equation(1.1),understood as an equation for v(τ,t),is invariant under the transformations τ→ x and v(τ,t)→ v(x,t).Then

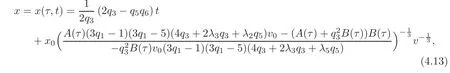
and(x,t)is obtained by inverting(4.13)as follows:

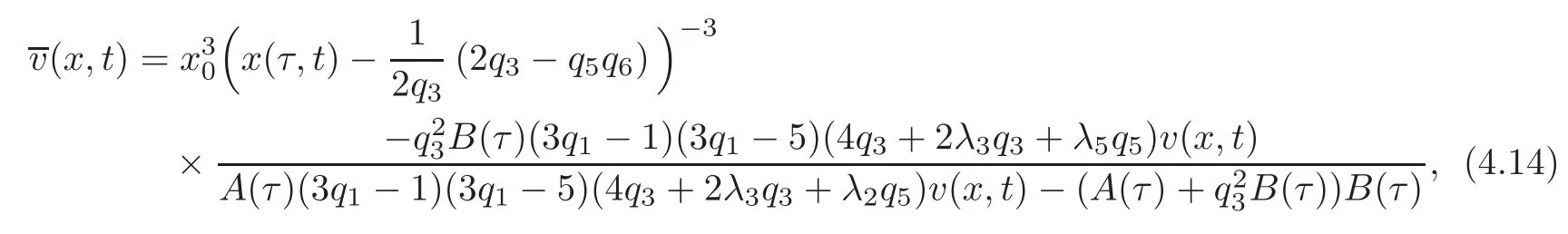
with A(τ)and B(τ)given by(4.11)and(4.12),respectively.

Theorem 4.2Assume that the OWW equation(1.1),understood as an equation for w(τ,t),is invariant under the transformations τ→ x and w(τ,t)→(x,t).Then

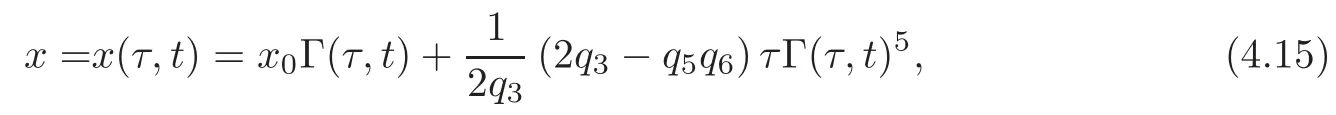
where Γ(τ,t)satisfies the following system:

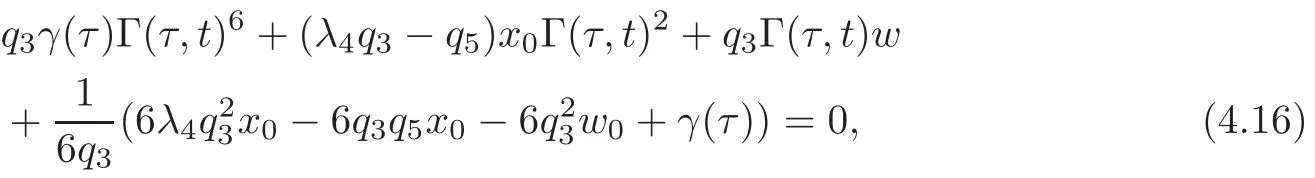
and(x,t)is obtained by inverting(4.15)–(4.16)as follows:

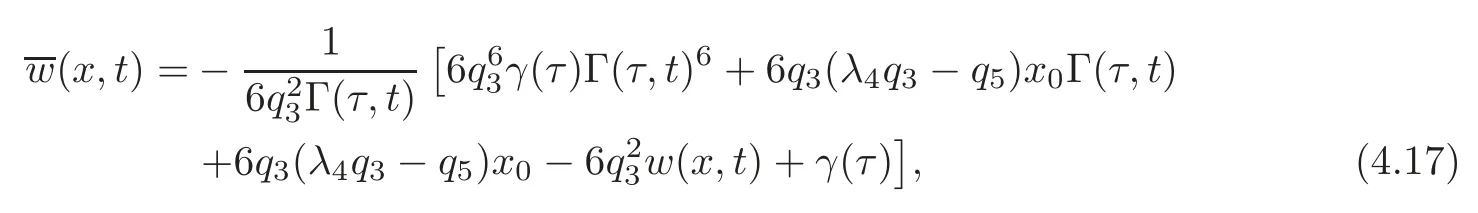
with

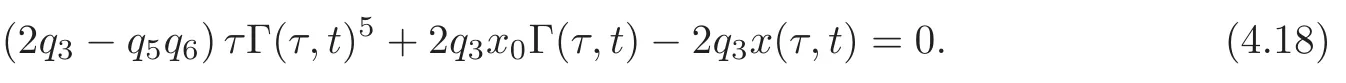
Similarly,taking τ and x as the “old” independent variables,we can obtain the following results.

Theorem 4.3Suppose that the OWW equation(1.1),understood as an equation for v(x,ε),is invariant under the transformations εt and v(x,ε)(x,t).Then

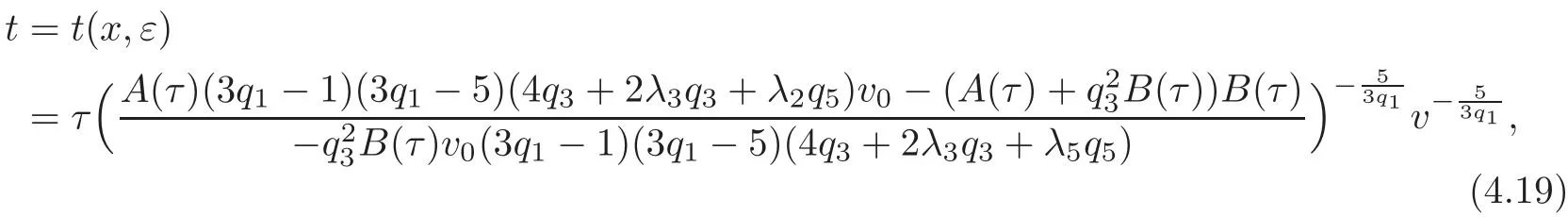
and(x,t)is obtained by inverting(4.19)as follows:

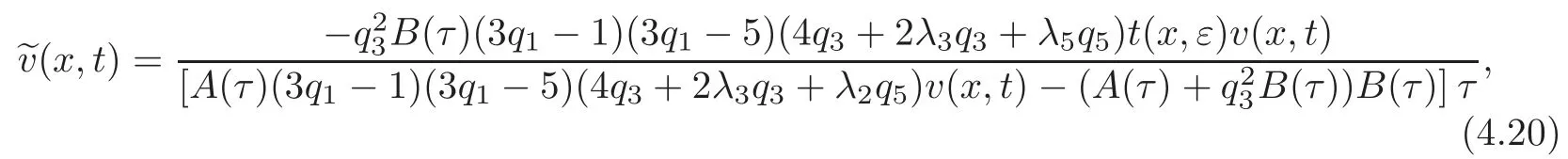
with A(τ)and B(τ)given by(4.11)and(4.12),respectively.

Theorem 4.4Assume that the OWW equation(1.1),understood as an equation for w(x,ε),is invariant under the transformations εt and w(x,ε)(x,t).Then

whereΓ(x,ε)satisfies the system(4.16),and(x,t)is obtained by inverting(4.21),(4.16)as follows:

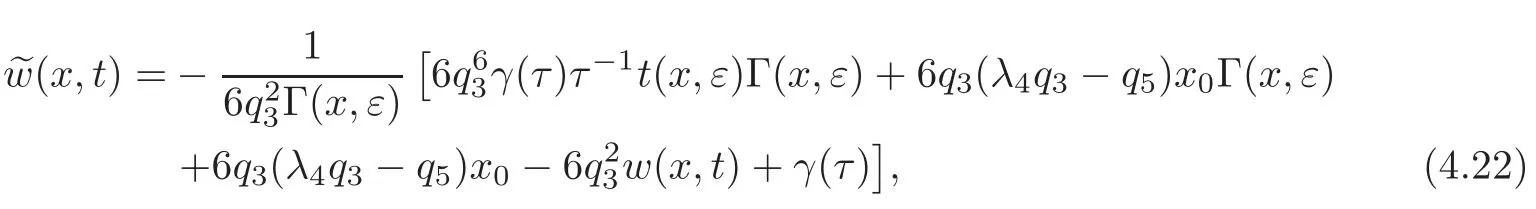
with

In what follows,we can investigate the SK(AOWW)equation.Following the foregoing theory,we can obtain similar Darboux transforms.

With initial conditions v0=v(0,τ),w0=w(0,τ),x0=x(0,τ)and t0=t(0,τ)= τ,we have a system for the flow of the vector fields obtained in Theorem 3.4 and given by

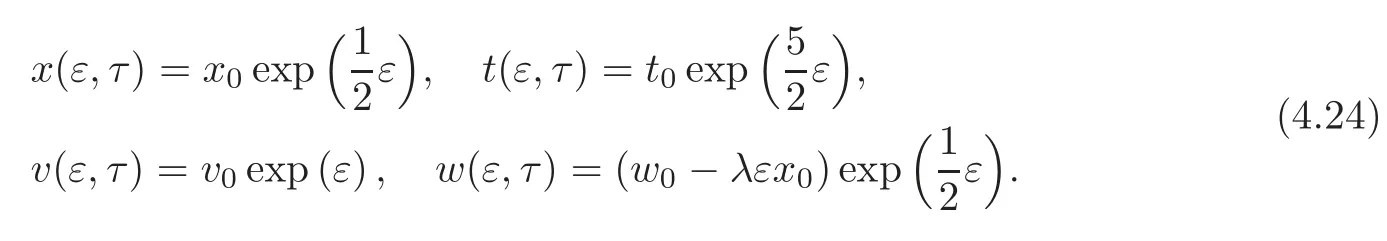
As in the OWW equation case,we do not calculate explicitly u(ε,τ),since this function is completely determined by v(ε,τ)and w(ε,τ).

For simplicity,we consider the SK equation(3.2)as an equation for w(τ,t)and w(x,ε).In the same way as stated in the OWW equation,we have the following theorem.

Theorem 4.5(i)Suppose that the SK(AOWW)equation(3.2),understood as an equationforw(τ,t),is invariant under the transformationsandw(τ,t)(x,t).Then

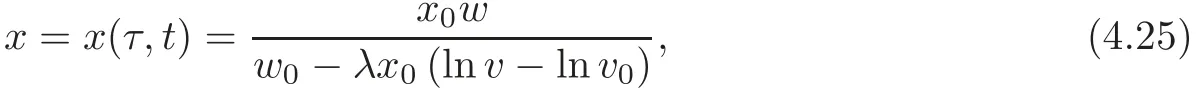
and(x,t)is obtained by inverting(4.25)and replacing into

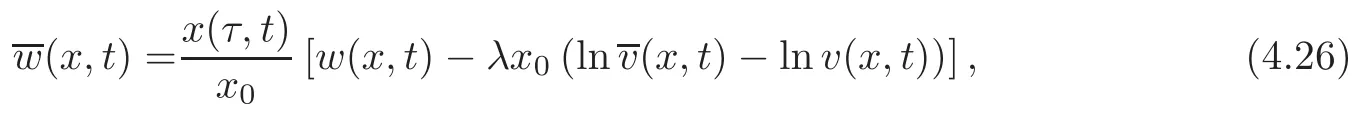
where(x,t)can be derived from(4.24)

withv(x,t)determined by(4.24).

(ii)Assume that the SK(AOWW)equation(3.2),understood as an equation forw(x,),is invariant under the transformationsεtandw(x,ε)(x,t).Then

and(x,t)is obtained by inverting(4.28)and replacing into

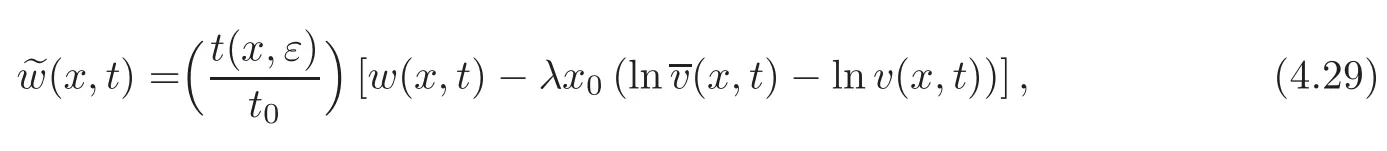
where(x,t)can be derived from(4.24)

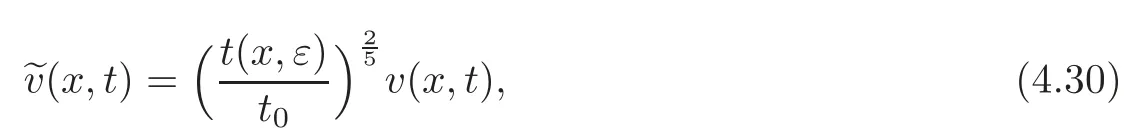
with v(x,t)is determined by(4.24).

Following the foregoing method,by virtue of the pseudo-potential variables v(x,t),w(x,t)and generalized symmetries,we present Darboux transformations of the OWW equation(1.1)and the(SK)AOWW equation(3.2),respectively.These formulae are used to find families of non-trivial solutions to the OWW equation and SK(AOWW)equation.

5 Conclusions and Discussions

In this paper,we have shown that combining generalized symmetries with the nonlocal condition can result in a variety of applications.The main new progresses made in this paper in the general aspect of evolution equations are given as follows:

(i)The generalized symmetries can be used to investigate the initial value problems.

(ii)The generalized symmetries can be used to construct Darboux transformations.

(iii)Lie algebras and generalized symmetries can be obtained from new pseudo-potential systems and vice versa.

(iv)Di ff erent kinds of Darboux transformations may assume the same in finitesimal forms,and then new kinds of Darboux transformations may be obtained from old ones.

(v)New finite-dimensional pseudo-potential systems can be solved by generalized symmetries and related Darboux transformations,and then the original evolution equation can be investigated from lower-dimensional ones owing to the existence of generalized symmetries.

The above results are realized especially for the fifth-order evolution equation,OWW and AOWW equations.For an OWW equation,it admits a new class of pseudo-potential systems resulting in its Lie algebras,generalized symmetries,initial value problems and Darboux transformations.Since such pseudo-potential systems are of the Riccati type,more information about their bilinear forms are also researched through the Cole-Hopf transformation.

For the purpose of extending applicability of the generalized symmetry to obtain analytic solutions of the OWW and AOWW equations,we introduce two new pseudo-potential variables v and w to form a new class of pseudo-potential systems,so that the original generalized symmetries can be transformed to some local symmetries of the new systems.Based on the generalized symmetries,we can investigate Lie algebras,initial value problems and Darboux transformations,et al.By means of the Darboux transformations,the analytic solutions of OWW and AOWW equations are obtained via the transformations of trivial solutions.Considering the complete local symmetries of the pseudo-potential systems,we can further achieve rich group invariant solutions,such as rational solutions,special function solutions,solitary wave solutions and periodic function solutions,et al.

However,in this paper,it still remains unclear what kind of pseudo-potential systems can be used to construct the generalized symmetries of the original evolution equation and what kind of generalized symmetries can be applied to obtain nontrivial solutions.The integrability of the pseudo-potential systems should be further investigated.Furthermore,one may consider soliton solutions,rational solutions,peakon solutions,breather solutions and algebraic geometry solutions of the completely integrable pseudo-potential systems to achieve corresponding solutions of the OWW and AOWW equations,respectively.It is quite reasonable and meaningful that these matters merit our further study.

AcknowledgementThe authors express their sincere thanks to the referees for their careful reading of the manuscript and constructive suggestions.

[1]Anderson,I.M.,Kamran,N.and Olver,P.J.,Internal,external and generalized symmetries,Adv.Math.,100,1993,53–100.

[2]Bluman,G.W.and Kumei,S.,Symmetries and Differential Equations,Springer-Verlag,New York,1989.

[3]Bluman,G.W.,Temuerchaolu and Anco,S.,New conservation laws obtained directly from symmetry action on a known conservation law,J.Math.Anal.Appl.,322,2006,233–250.

[4]Bluman,G.W.,Tian,S.F.and Yang,Z.Z.,Nonclassical analysis of the nonlinear Kompaneets equation,J.Eng.Math.,84,2014,87–97.

[5]Chern,S.S.and Tenenblat,K.,Pseudo-spherical surfaces and evolution equations,Stud.Appl.Math.,74(1),1986,55–83.

[6]Chen,Y.and Hu,X.R.,Lie symmetry group of the nonisospectral Kadomtsev-Petviashvili equation,Z.Naturforsch A.,62(a),2009,8–14.

[7]Dodd,R.K.and Gibbon,J.D.,The prolongation structure of a higher order Korteweg-de Vries equation,Proc.R.Soc.Lond.A,358,1978,287–296.

[8]Fan,E.G.,Multiple travelling wave solutions of nonlinear evolution equations using a uni fied algebraic method,J.Phys.A:Math.Gen.,35,2002,6853–6872.

[9]Galas,F.,New nonlocal symmetries with pseudopotentials,J.Phys.A:Math.Gen.,25,1992,L981–L986.

[10]Guthrie,G.A.and Hickman,M.S.,Nonlocal symmetries of the KdV equation,J.Math.Phys.,26,1993,193–205.

[11]Huang,Q.and Qu,C.Z.,Symmetries and invariant solutions for the geometric heat flows,J.Phys.A:Math.Theor.,40,2007,9343–9360.

[12]Hernandez-Heredero,R.and Reyes,E.G.,Nonlocal symmetries and a Darboux transformation for the Camassa-Holm equation,J.Phys.A:Math.Theor.,42,2009,182002.

[13]Itô,M.,An extension of nonlinear evolution equations of the K-dV(mK-dV)type to higher orders,J.Phys.Soc.,49,1980,771–778.

[14]Ibragimov,N.H.,CRC Handbook of Lie Group Analysis of Differential Equations,vol.1,CRC Press,Boca Raton,Florida,1994.

[15]Kaup,D.J.,On the inverse scattering problem for cubic eigenvalue problems of the class Ψxxx+6QΨx+6RΨ = λΨ,Stud.Appl.Math.,62,1980,189–216.

[16]Kupershmidt,B.A.,A super Korteweg-de Vries equation:An integrable system,Phys.Lett.A,102,1984,213–215.

[17]Kudryashov,N.A.and Sukharev,M.B.,Exact solutions of a non-linear fifth-order equation for describing waves on water,J.Appl.Math.Mech.,65,2001,855–865.

[18]Lax,P.D.,Integrals of nonlinear equations of evolution and solitary waves,Comm.Pure Appl.Math.,21,1968,467–490.

[19]Levi,D.and Winternitz,P.,Lie point symmetries and commuting flows for equations on lattices,J.Phys.A:Math.Gen.,35,2002,2249–2262.

[20]Lou,S.Y.,A(2+1)-dimensional extension for the sine-Gordon equation,J.Phys.A:Math.Gen.,26,1993,L789–L791.

[21]Lou,S.Y.and Hu,X.B.,In finitely many Lax pairs and symmetry constraints of the KP equation,J.Math.Phys.,38,1997,6401–6427.

[22]Noether,E.,Invariante variations probleme,Nachr.Konig.Gesell.Wissen.Gottingen,Math.Phys.Kl.,1918,235–257(see Transport Theory and Stat.Phys.1,1971,186–207 for an English translation).

[23]Olver,P.J.,Applications of Lie Groups to Differential Equations,2nd edition,Springer-Verlag,New York,1993.

[24]Olver,P.J.,Hamiltonian and non-Hamiltonian models for water waves,Lecture Notes in Physics,vol.195,Springer-Verlag,New York,1984.

[25]Qu,C.Z.,Potential symmetries to systems of nonlinear di ff usion equations,J.Phys.A:Math.Theor.,40,2007,1757–1773.

[26]Qu,C.Z.and Zhang,C.R.,Classi fication of coupled systems with two-component nonlinear di ff usion equations by the invariant subspace method,J.Phys.A:Math.Theor.,42,2009,475201.

[27]Reyes,E.G.,On nonlocal symmetries of some shallow water equations,J.Phys.A:Math.Theor.,40,2007,4467–4476.

[28]Reyes,E.G.,Nonlocal symmetries and the Kaup-Kupershmidt equation,J.Math.Phys.,46,2005,073507.

[29]Sawada,K.and Kotera,K.,A method for finding N-soliton solutions of the KdV and KdV-like equation,Prog.Theor.Phys.,51,1974–1355.

[30]Tian,S.F.and Zhang,H.Q.,Riemann theta functions periodic wave solutions and rational characteristics for the nonlinear equations,J.Math.Anal.Appl.371,2010,585–608.

[31]Tian,S.F.and Zhang,H.Q.,Lax pair,binary Darboux transformation and new grammian solutions of nonisospectral Kadomtsev-Petviashvili equation with the two-singular-manifold method,J.Nonlinear Math.Phys.,17(4),2010,491–502.

[32]Tian,S.F.and Zhang,H.Q.,A kind of explicit Riemann theta functions periodic waves solutions for discrete soliton equations,Commun.Nonlinear Sci.Numer.Simulat.,16,2011,173–186.

[33]Tian,S.F.and Zhang,H.Q.,Super Riemann theta function periodic wave solutions and rational characteristics for a supersymmetric KdV-Burgers equation,Theor.Math.Phys.,170(3),2012,287–314.

[34]Tian,S.F.and Zhang,H.Q.,On the integrability of a generalized variable-coefficient Kadomtsev-Petviashvili equation,J.Phys.A:Math.Theor.,45,2012,055203.

[35]Tian,S.F.and Zhang,H.Q.,On the integrability of a generalized variable-coefficient forced Korteweg-de Vries equation in fluids,Stud.Appl.Math.,132,2014,212–246.

[36]Vinogradov,A.M.and Krasil’shchik,I.S.,A method of calculation of higher symmetries of nonlinear evolution equations and nonlocal symmetries,Dokl.Akad.Nauk SSSR,253,1980,1289–1293.

[37]Yan,Z.Y.,The new tri-function method to multiple exact solutions of nonlinear wave equations,Phys.Scr.,78,2008,035001.

[38]Zhang,S.L.,Lou,S.Y.and Qu,C.Z.,New variable separation approach:Application to nonlinear di ff usion equations,J.Phys.A:Math.Gen.,36,2003,12223–12242.