应用型本科高校线性代数教学改革探讨
2015-06-01王贞
王 贞
(池州学院 数学与计算机科学系,安徽 池州 247000)
1 应用型本科高校线性代数教学现状
1.1 教材重理论轻应用
线性代数教材,以同济六版[1]为例,主要介绍定义、定理和相关计算,内容重理论、偏抽象,对一些概念的背景来源,知识的实际应用等方面则很少涉及。对于应用型本科高校来说,这样的教学内容很难使学生对其产生兴趣,更重要的是,它不符合应用型人才培养需求。
1.2 教学课时不足,教学内容受限
线性代数教学时数有限,一般为32-48课时。课时较少,内容抽象,其内容为:行列式、矩阵及其运算、矩阵的初等变化与线性方程组、向量组的线性相关性、相似矩阵与二次型等,对于其核心内容“线性空间与线性变换”就只能点到为止。由于课时不足,致使学生没学到线性代数的精华内容。
1.3 考核制度不完善
线性代数课程考核,主要考查平时出勤率以及期末卷面成绩。期末试卷,主要是考查学生对基本概念的理解,以及判断、计算、推理、证明等,缺少对解决实际问题能力的考核。这样的考核制度,导致很多学生只注重理论知识的学习,忽视了能力培养。
2 应用型本科高校线性代数教学改革思路
2.1 教学内容改革
2.1.1 增加实际应用背景知识 当前很多教材,主要介绍基础知识,缺乏知识来源和联系实际生活等内容,学生学习起来,感觉枯燥无味。因此,我们可以借鉴美国著名教育家David Lay教授编著的《线性代数及其应用》[2],适当插入一些背景知识或者与我们身边相关的实际生活问题,提高学生学习兴趣,促进学生自主学习。
2.1.2 精炼教学内容,突出重点内容 李尚志老师认为,线性代数主要内容:空间为体,矩阵为用[4]。我们讲解矩阵内容时,要突出其重点地位,根据应用型人才培养目标,引用一些具体实例,如人口迁移问题等,努力培养学生利用矩阵解决实际问题的能力。行列式的计算并不是线性代数的重点内容,我们只需利用行列式性质掌握一些基本的计算方法即可。我们需要向学生介绍如何利用Matlab计算行列式,在很多实际问题中关于行列式的计算都用Matlab执行。此外,对于克拉默法则,同学们只需知道这个法则即可,不需要利用这个法则来解给定的方程组。
2.1.3 根据内容采用分层教学 由于教学课时有限,教学内容很难满足所有同学的需求。为了解决这个问题,我们可以采取分层教学模式,在大二上学期,面向全体理工、经管等专业学生,开设线性代数公共课;在大三上学期或下学期,面向继续深造或者对线性代数感兴趣的学生,开设线性代数选修课。线性代数公共课,内容基础,突出应用;线性代数选修课,深化理论知识,培养学生的逻辑思维能力,为进一步夯实基础。
2.2 教学方法改革
2.2.1 整体性教学 在授课过程中,我们要善于引导学生注意前后知识的衔接,帮助学生系统性掌握基础知识。例如判断n维向量组A:α1,α2,…,αm的线性相关性,可以通过判断线性方程组x1α1+x2α2+…+xmαm=0 是否有非零解。而对线性方程组求解问题,我们只需比较矩阵A=(α1,α2,…,αm)的秩与m的大小关系。从这样问题出发,可以将矩阵、线性方程组的解、向量组的线性相关性内容联系起来,形成一个整体。
2.2.2 借助计算机辅助教学 当我们还一如既往地讲解行列式的计算方法、求逆矩阵、解线性方程组时,我们的学生很难解决实际生活中的数学问题。例如,Wassliy Leontief利用500个变量的500个线性方程问题描述美国经济问题[3]。解这样的线性方程组,如果纯粹手算,是一件繁冗复杂的事情。我们可以引入Matlab数学软件来解决这一问题。此外,Matlab软件还可以求解行列式、方阵的逆、线性方程组、特征值、特征向量等问题,有效帮助助学生解决实际生活问题。
2.2.3 以学生为中心 教学过程中,我们要以学生为中心,尊重学生经验。例如,我们在讲解施密特正交化的时候,可以先给定线性无关的向量组a1,a2,如何由这组向量组得出两个正交的向量组呢?我们可以以a1为给定向量,将a2沿着a1方向和垂直a1方向进行分解,分别得到向量a'2和b2,从而使得b2⊥a1,接下来如何由a1,a2表示b2呢?以问题为突破口,诱导学生思考,以几何为工具,加强学生感性认识。最后,由这样简单直观的情况延伸到空间中的3个线性无关组正交化,继而抽象到n(n>3)个线性无关的向量组如何正交化问题,施密特正交化过程也就不再生涩难懂了。
2.2.4 以应用为导向 我们在讲解某些知识点时,可以引入一些实际应用问题,从而激发学生学习兴趣,增强学习动力。例如,我们在讲解矩阵的运算以及矩阵的逆的时候,可以引入利用矩阵编制Hill密码问题[6]。比如我们要发出信息linear,现需要利用矩阵乘法给出加密方法和加密后得到的密文,并给出相应的揭秘方法。假定空格和26个英文字母依次对应整数0~26(见下表)。
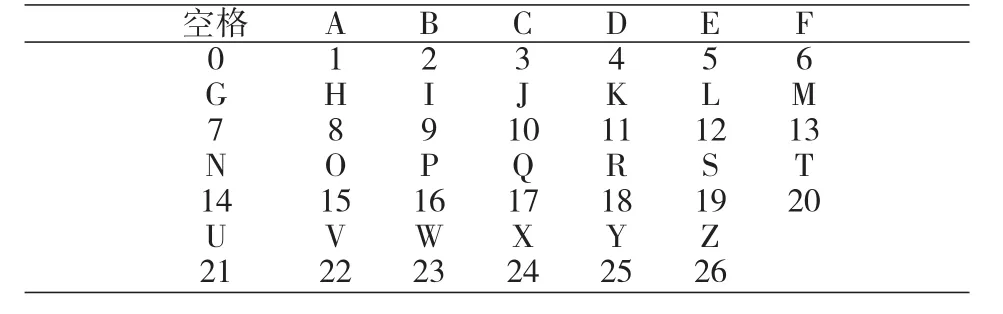
空格及字母的整数代码表
假设单词从左到右,每3个字母分为一组,并将对应的3个整数排成3维的行向量。
通过以上所述假定,信息linear对应两个向量x1=(12,9,14),x2=(5,1,18).我们给定可逆矩阵

使得密文
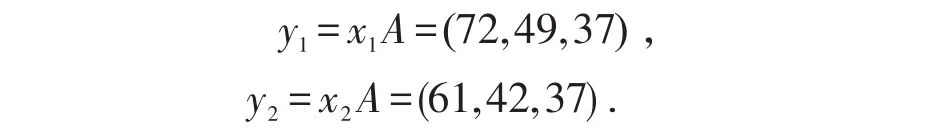
接收方收到的密文是72,49,37,61,42,37.接收方需要解码,则需要计算 (72,49,37)A-1和(61,42,37)A-1。
2.3 考核改革
对于线性代数的考核主要体现在三个方面:期末考试、实践教学、平时出勤与作业,它们占总评成绩比例可设为5:3:2。对于实践教学的考查,可以放在某些章节结束后即可考查,这样可以避免期末考前突击现象的发生。
3 结束语
MIT的G.Strang教授提出“让线性代数向世界开放”口号,我希望通过线性代数课程的教学改革,激发学生学习兴趣,让更多同学不仅能够掌握其基本知识,还善于利用这些知识去解决一些实际问题,提高自己在现代社会中的竞争力。
[1]同济大学数学系.工程数学线性代数[M].6版.北京:高等教育出版社,2014.
[2]David C Lay.Linear and its applications[M].4th Ed.New Jersey:John Wiley&Sons,Inc,2009.
[3]陈怀琛,龚杰民.线性代数实践及Matlab入门[M],北京:电子工业出版社,2005.
[4]李尚志.线性代数教学改革漫谈[J].教育与现代,2004(01):30-31.
[5]Stang G.Introduction to Linear Algebra[M].3rd ed.Wellesley MA:Welley-CambridgePress,2009.
[6]杨威,高树屏,线性代数计算与应用指导[M].西安:西安电子科技大学出版社,2009(4):98-102.
