基于实测载荷谱的侧架寿命分析*

韩朝霞，孙守光，赵方伟

(北京交通大学 机械与电子控制工程学院，北京100044)

基于实测载荷谱的侧架寿命分析*

韩朝霞，孙守光，赵方伟

(北京交通大学 机械与电子控制工程学院，北京100044)

随着铁路提速重载的发展，铁路货车转向架零部件的疲劳裂损率增加。本文通过我国几条典型线路实测，得到我国铁路货车的实测载荷谱。利用有限元仿真得到载荷—应力的转化系数，由实测载荷谱得到应力谱，基于该应力谱计算转向架侧架的疲劳寿命，并和AAR载荷谱的疲劳寿命对比分析，验证实测载荷谱的可用性。

侧架;实测载荷谱;疲劳寿命;循环特征

在随机载荷作用下，大部分工程结构的失效是由疲劳破坏造成的。因此，人们对工程结构疲劳问题的研究工作越来越重视。随着铁路货车运行速度以及载重的逐步提高，作为车辆转向架的侧架［1］疲劳裂纹［2］的失效问题显得日益突出，因此，对货车侧架的疲劳问题进行研究意义重大。

作为转向架的重要组成部分，运用中的侧架承受拉、压、冲击、弯曲等多种交变载荷的作用。目前，只有AAR的载荷谱［3］能够给我们提供一些数据及模型的参考。但是，由于我国地域广阔，地理形势复杂，修建的铁路远远比美国AAR标准建立时的试验条件复杂，因此若直接将AAR的载荷谱应用于我国铁路的货车设计、制造及寿命评估，不能满足我国铁路运输的发展需求。因此，我们迫切需要建立符合我国大铁路实际运营工况的载荷谱。本文就是在运营线路上进行侧架动态载荷测试，结合有限元分析［4］的数据，编制出符合我国铁路工况的载荷谱，并基于该载荷谱估算侧架寿命，验证了实测载荷谱的可用性，具有重要的意义。

1 有限元分析

(1)有限元模型的建立

利用三维软件Solidworks对侧架进行实体建模后，再导入有限元分析软件Hypermesh选用Solid45单元划分网格。划分单元后结构离散网格模型见图1，然后导入ANSYS进行有限元分析计算。

(2)约束设置及加载情况

基于AAR标准的侧架载荷谱是通过取摇枕浮沉总载荷之半近似作为侧架垂向载荷，由载重90.7 t敞车的重空车摇枕浮沉总载荷线路环境事件百分率谱换算

出相应的侧架垂向载荷谱。

图1 侧架离散网格模型

因此有限元分析计算时，分两种情况计算。一种是在侧架轴箱弹簧支撑处施加垂向弹性约束﹑导框处施加横向弹性约束，在弹簧承台处施加垂向载荷，载荷大小依据AAR机务标准M－203－05《铸钢转向架侧架设计和技术规范》取为349.9 kN。另一种是在弹簧承台处施加三向弹性约束，在侧架轴箱弹簧支撑处施加垂向载荷，载荷大小依据AAR机务标准M－203－05取为349.9 kN。

(3)有限元分析计算结果

两种约束载荷施加后，结果相近。侧架在垂直载荷工况下的应力分布如图2所示。列出各点的应力值如表1所示。比较各关键点的应力大小，并结合参考文献［1］选取最大应力位置的载荷—应力转化系数0.315。

2 载荷谱与应力谱转换

(1)动载荷测试与载荷谱编制

在转K6转向架处安装专门定制的承载鞍传感器。选用德国数字采集系统IMC SL宽温系列测试仪器，在北京到广州，北京到成都，北京到哈尔滨3条线路上分别往返3次进行全程连续测试，各条线路测试里程见表2。

图2 侧架在垂向载荷作用下应力云图

表1 损伤量最大的4个节点应力

表2 各线路测试里程

各条线路的测试里程都达到AAR标准的测试里程要求。试验时最高运行速度为80 km/h，牵引吨位为5 000 t，数据采集时采样频率为500 Hz。采用雨流计数法［5］对采集数据进行处理，最后得到侧架的载荷—时间历程，并编制载荷谱。

(2)侧架应力谱编制

试验测取同一个转向架的4个承载鞍。4个承载鞍的载荷在时间历程上若直接相加，则从载荷—时间历程上可以看出转向架一侧的承载鞍最大值的位置刚好同另一侧承载鞍最小值的位置同步，因此若取4个承载鞍载荷加和的一半作为侧架的载荷，则侧架载荷被拉低，计算出的寿命不准确，此获取侧架载荷的方法是不可取的。对同一侧架两端的承载鞍分别编制载荷谱，得出两者除了在载荷—时间历程上稍有不同之外，在载荷谱的统计分析方面一样，因此可以取单个承载鞍载荷的两倍作为侧架载荷，并进行处理得到侧架载荷谱。上文已计算出载荷—应力传递系数，按照准静态法将各损伤最大点的载荷谱转化为应力谱。

(3)AAR载荷谱编制

取摇枕总载荷之半近似作为侧架垂向载荷，由载重90.7 t敞车的重车摇枕浮沉总载荷线路环境事件百分率谱换算出相应的侧架垂向载荷谱。换算系数根据(试验车载重+自重)/(90.7 t敞车载重+自重)计算得0.76。按载荷与应力成线性关系由侧架载荷谱换算出侧架在垂向载荷谱作用下的应力谱。

3 基于载荷谱的侧架寿命估算

(1)对数S－N曲线斜率的确定

根据AAR设计基准推荐的S－N曲线如图3所示。经验表明，在大多数情况下，铸件疲劳裂纹始发于有明显铸造缺陷或局部应力集中的区域。对导致疲劳裂纹发生的铸造缺陷按3类进行分析:小缺陷(球状)，较少见，kf为疲劳降低系数，kf=1.25;大缺陷(裂纹状)，罕见，kf=2～3;中等缺陷(夹渣、疏松、缩孔)，最常见，kf= 1.5～2。有关数据表明，铸件中kf=1.5～2的中等缺陷有很高的出现概率。因此，kf=1.5～2的中等缺陷代表铸件的正常质量［6］。北美铁路协会AAR的统计数据表明，铸造缺陷是摇枕在运用中发生疲劳裂纹的主要原因。

图3 B级钢S－N曲线

考虑疲劳降低系数kf=1.5，2，2.5，3时的侧架寿命。已知kf=1时的侧架B级钢S－N曲线，对其取双对数，则双对数S－N曲线的绝对斜率为:，计算得到k=0.12，即k1=0.12，k2=k1/2;其中k1、k2为理想S－N曲线的绝对斜率，见图4。

图4 理想S－N曲线

图中Ni为第i个应力级下出现损坏的循环数;Si为按Ni次循环损坏计算的疲劳极限;Se为疲劳极限内出现损坏的应力;Ne为Se应力级下出现损坏的循环数。

(2)Goodman图的参数确定(图5)

图5 Goodman图

R为最小/最大应力比值。Smax为最大应力。Smin为最小应力。

由R=－1时的S－N曲线以及强度极限σb=483 MPa即可得到Goodman图的截距b和斜率m，列于表3中。

表3 Goodman图的截距和斜率

(3)按累积损伤理论进行疲劳寿命估算

用上文计算出的m，b，k值，结合S－N曲线以及应力谱计算侧架的疲劳寿命。其中，

式中k为S－N曲线斜率的绝对值，Sr是应力范围，αi为作用给第i应力级占总循环数的百分数，R为循环特征Smin/Smax，β是每公里谱循环数，各测试线路的每公里谱循环数见表4。

表4 测试线路每公里谱循环数

(4)计算结果及分析

空车运行对侧架产生的损伤极小，可以忽略不计。重车运行情况决定着侧架的疲劳寿命。因此，本文选择重车运用条件下的AAR载荷谱和线路实测载荷谱。

在AAR载荷谱和实测载荷谱作用下，假设以AAR载荷谱计算的寿命为基准，此处设为1，则侧架在实测载荷谱作用下的相对疲劳寿命为实测寿命除以AAR载荷谱寿命。侧架在AAR载荷谱以及实测载荷谱作用下的疲劳寿命见图6。

图6 侧架在不同载荷谱下的疲劳寿命

从图6中可以看出kf在1.5～2.0之间时，该系数对侧架寿命的影响较大。出现这种状况的原因是kf较小变化能引起应力较小变化，但是，应力与寿命之间不是线性关系，而是对数值的线性关系。因而kf较大时，应力变化较大，引起寿命的剧烈变化。或者可以说当疲劳缺口系数达到一定程度时，载荷对寿命的影响也变的不明显，此时侧架的寿命主要表现为疲劳裂纹扩展寿命。

由图6结果分析可知，不同线路计算结果随着疲劳降低系数的总趋势相同。但在同等疲劳降低系数下的AAR载荷谱计算的寿命要比实测载荷谱计算的寿命低。分析两者试验条件，可知AAR载荷谱的测试速度为39.7 km/h，而本次国内大铁路的试验速度最高达到80 km/h。速度对转向架零部件的疲劳寿命有很大影响。速度越高，侧架疲劳损伤越大，寿命越短。分析其原因，首先比较不同线路以及AAR载荷谱的循环特征所占百分比，如图7所示。从图中可知，AAR载荷谱试验的循环特征大部分集中在0.93～1之间，我国实测线路的循环特征集中在0.81～0.92之间。根据影响循环特征的因素分析可知，同样的材料，当循环特征不同时，疲劳曲线不同。低周疲劳区，循环特征越大，同样的应力下的寿命越大。高周疲劳区，循环特征越大，同等寿命下的应力越大。

其次，载荷谱的测试方法也不一样，实测载荷谱的动应力直接从轮对经过一系悬挂在承载鞍处测得，AAR载荷谱的动应力是从轮对经过一系悬挂和二系悬挂在摇枕处获得，因此两者具有明显的差别。实测载荷谱计算出的寿命更贴近以后实际运营中侧架的疲劳寿命。

国内大铁路上不同线路的疲劳寿命差别明显，见图8。

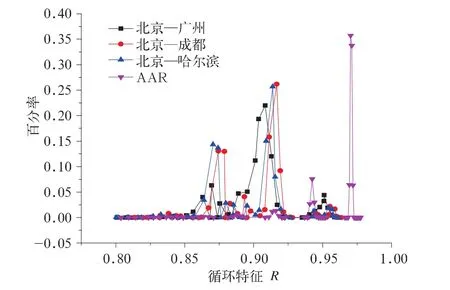
图7 循环特征对比图

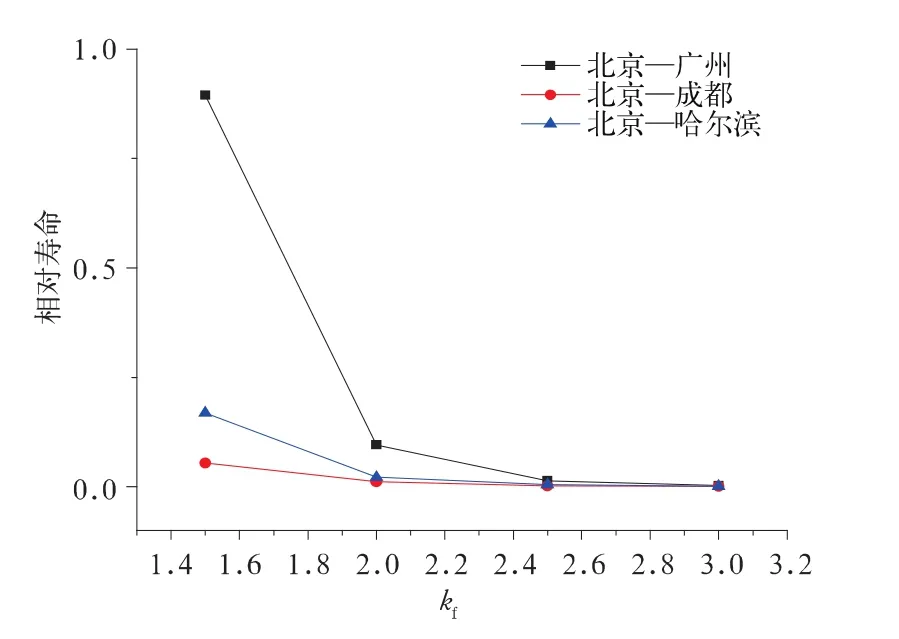
图8 各测试线路寿命

从图8中可以看出，北京—成都的线路测试出来的侧架寿命最短，北京到哈尔滨的侧架寿命次之，北京—广州的侧架寿命最长。分析3条线路可知，由于地理因素的差异，北京—成都的线路工况最差。该条线路上修建有最多的曲线和道岔。

由于试验条件的限制，本文忽略了侧架承受的横向载荷以及交叉杆载荷的作用。要想得到更精确的载荷谱，需要对侧架的横向载荷以及交叉杆载荷补充试验。

4 结 论

(1)不同因素对转向架侧架的寿命均有重要影响，包括疲劳降低系数，货车运行速度，线路工况等。

(2)在疲劳降低系数为1.5～2时，转向架侧架寿命较高，随着疲劳降低系数的增大，对寿命的影响明显。

(3)运行速度越快，动应力越明显，循环特征越小，应力越大，疲劳寿命越小。

(4)曲线、道岔越多，对动应力影响越大，侧架寿命越短。

需结合我国铁路线路工况、载重、速度以及生产侧架水平实际情况来编制载荷谱，为将来提速重载的稳定发展做好准备。

［1］ 丁 敏，吴作伟，王淑青，陈政南.货车侧架疲劳裂纹检修数据的统计分析［J］.电力机车技术，2002，25(3):42-44.

［2］ 高镇同.疲劳应用统计学［M］.北京:国防工业出版社，1986.

［3］ 刘德刚，侯卫星，王凤洲，等.基于有限元技术的构件疲劳寿命计算［J］.铁道学报，2004，26(2):47-51.

［4］ 周 俊，童小燕.雨流计数的快速实现方法［J］.科学技术与工程，2008，8(13):3545-3547，3558.

［5］ 刘志明.随机载荷下焊接构架疲劳寿命及可靠性研究［D］.北京:北方交通大学，2001.

Study of Side Frame Fatigue Life Based on Measured Load Spectrum

HAN Zhaoxia，SUN Shouguang，ZHAO Fangwei
(School of Mechanical，Electronic and Control Engineering，Beijing Jiaotong University，Beijing 100044，China)

The rate of fatigue crack on the side frame of freight vehicles is increasing with the acceleration and overloading of railway.This paper obtained measured load spectrum of freight vehicles on national railway through the experiment on several typical railways.The stress spectrum is then calculated with the load-stress transforming factors by FEM analysis.The comparison between fatigue life which is calculated by measured load spectrum and AAR load spectrum shows the reliability of measured load spectrum.

side frame;measured load spectrum;fatigue life;cycling characteristics

U272

A

10.3969/j.issn.1008－7842.2015.01.03

1008－7842(2015)01－0015－04

*铁道科技发展基金项目(2011J014－A)

0—)女，硕士研究生(

2014－07－20)