基于FIR滤波和数学形态学的心电信号预处理算法

郑秀玉，卢瑞祥

深圳市计量质量检测研究院 医疗器械实验室，广东 深圳 518055

基于FIR滤波和数学形态学的心电信号预处理算法

郑秀玉，卢瑞祥

深圳市计量质量检测研究院 医疗器械实验室，广东 深圳 518055

本文针对心电信号的工频干扰和基线漂移，提出一种基于有限长单位冲激响应（FIR）滤波器和数学形态学的综合滤波方法，该方法首先采用形式简单的FIR平滑滤波器滤除心电信号的50 Hz工频及其高频谐波，接着将数学形态滤波器应用于滤除基线漂移。实验结果表明，本文设计的综合滤波方法能够有效地滤除工频干扰和基线漂移，为心电信号进一步的分析提供良好的基础。

心电信号；数学形态学；有限长单位冲激响应滤波器

0 前言

心电图（Electrocardiogram，ECG）是临床上常规检查方法之一，它对某些疾病尤其是心血管疾病的诊断具有重要意义。心电信号作为心脏电活动在人体体表的表现，信号比较微弱，极易受环境的影响。其含有不同类型的噪声，主要有工频干扰和基线漂移。由于这些噪声与信号混叠，影响了心电各段波形特征的正确识别。为了消除心电信号中的主要干扰，提高检测准确率，人们提出了许多方法对心电信号进行预处理。如有限长单位冲激响应（Finite Impulse Response，FIR）滤波器、自适应滤波器、小波滤波器、神经网络滤波方法和数学形态学滤波器等。自适应滤波器算法复杂，且需要附加参考信号[1]。小波滤波方法计算量大，处理时间长，不适于对算法实时性要求较高的场合[2-3]。神经网络滤波方法计算复杂、速度较慢[4]。FIR滤波器虽然结构简单，易于实现，但由于ECG信号和基线漂移的频带相重叠，仅采用FIR滤波器方法在滤除噪声的同时，往往也会损失ECG信号中许多极有诊断价值的波形信息[5]。随着非线性滤波技术的发展，数学形态学提供了一种非常有效的非线性信号处理方法，其建立在积分几何和随机集合论基础上的，根据信号的局部特征对信号进行分析和识别，可以用于ECG信号的滤波处理，在滤除噪声的同时可以较好地保持必要的心电几何信息不变。

本文概述了FIR滤波器和数学形态学的应用于心电信号滤波的原理，结合FIR滤波器和数学形态学滤波方法的优点，设计出基于FIR滤波和数学形态学的综合滤波方法。该方法首先采用形式简单的FIR平滑滤波器滤除心电信号的50 Hz工频及其高频谐波，接着将数学形态滤波器应用于滤除基线漂移。本文采用PTB标准数据库[6]进行研究，该数据库工频干扰为50 Hz，采样频率为1000 Hz。实验结果表明，本文设计的综合滤波方法能够有效地滤除工频干扰和基线漂移，为心电信号进一步的分析提供良好的基础。

1 FIR平滑滤波和数学形态学在心电信号预处理原理

1.1 FIR平滑滤波器

FIR平滑滤波是数字滤波方法中常被人们采用的方法，该方法算法简单，处理速度快，滤波效果较好[7-8]。使用FIR平滑滤波器对信号滤波时，实际上是拟合了信号中的低频成分，而把高频成分“平滑”出去。由于人体心电信号的频率较低，主要频率范围是0.05~100 Hz，而大部分能量又集中在0.5~45 Hz。可以采用FIR平滑滤波器滤除工频噪声及其高频谐波。

本论文采用PTB标准数据库进行研究，该数据库工频干扰为50 Hz，采样频率为1000 Hz。将FIR平滑滤波器运用于滤除该数据库心电信号的50 Hz工频及其高频谐波，该滤波器阶数必须为N=1000 Hz/50 Hz=20，即该滤波器传递函数为：

该FIR平滑滤波器对50 Hz工频及其高频谐波截止，且对100 Hz以后信号基本衰减到原信号的10％，即-10 dB（图1）。将该滤波器应用于PTB数据库中s0001_re.dat文件的滤除噪声后结果见图2。本文设计的20阶FIR平滑滤波器可以有效的滤除心电信号中的50 Hz工频及其高频谐波，对100 Hz以上的高频噪声抑制效果也不错。

图1 FIR平滑滤波器幅频特性

图2 原信号与FIR平滑滤波器滤波后信号波形图

1.2 数学形态学滤波器

FIR平滑滤波器虽然有效的滤除心电信号中的50 Hz工频及其高频谐波，但信号存在基线漂移，对信号的检测及特征提取影响很大。本文将数学形态学运算应用于一维信号处理中，利用这种非线性滤波方法对于噪声带来的奇异点敏感性来滤除心电信号中的噪声，实现对一维的ECG信号进行数学形态学滤波的目的（图3）。

图3 从二维到一维的映射

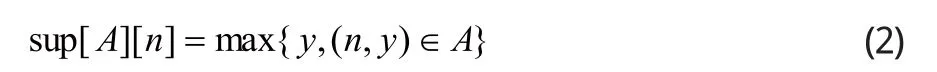
同理，对结构元素序列k(m）有

则信号f(n）关于结构元k(m）的形态学膨胀运算定义为：

信号f(n）关于结构元k(m）的形态学腐蚀运算定义为

图4 心电图信号进行运算处理后的结果

从图4可以清楚地看出，从原始ECG信号中分别减去其形态学开运算或闭运算后的结果，就可以得到原信号的峰值或谷值，这些波峰或波谷的宽度取决于所选择的结构元宽度。

对于含噪ECG信号而言，如果选择结构元的宽度小于ECG信号所有特征子波形的宽度，则对ECG信号进行开运算和闭运算后，ECG信号的所有特征子波形都会被保留，而信号中混杂的宽度小于结构元宽度的高频干扰则会被滤除。另一方面，有基线漂移的ECG信号可以认为是缓慢变化的信号上叠加宽度相对狭窄的ECG信号，因此，也可以用一组开、闭运算从原始信号中有选择地除去ECG特征波形，开运算移去正脉冲，而闭运算移去负脉冲。从而得到从原始信号中分离出来的基线漂移信号，再用原始信号减去基线漂移信号后，得到除去基线漂移的矫正后的ECG信号。

因此，本文选择了幅值为0的直线形的结构元素，设计了包含两组串联的数学形态学滤波器模块，这两个数学形态学滤波模块分别具有不同的结构序列。第一组结构序列宽度较大，其序列宽度大于心电特征波形P、Q、R、S、T宽度，进行开闭运算的结果，使得这些特征波形都被滤除，只剩下基线漂移信号，再用原信号减去获得的基线干扰信号，即可获得滤除了基线漂移干扰后的心电信号；第二组形态滤波器的结构序列宽度较窄，其序列宽度大于高频噪声信号宽度，而小于ECG特征波形P、Q、R、S、T的宽度，则开闭运算的结果，使得心电信号中的高频噪声信号被去除。这样在经过这两组不同的形态滤波器后，获得了滤除了高频干扰和基线漂移的信号（图5）。

图5 数学形态滤波流程图

采用上述数学形态学滤波器，对PTB标准心电数据库中的s0001_re.dat的第I导联的部分心电信号数据进行形态学滤波实验。对该信号采用第一组数学形态学滤波器模块滤波后结果见图6，其中开运算的结构元素的宽度M=190，闭运算的结构元素的宽度M=70。

图6 数学形态学滤波器去除心电图信号基线漂移效果

对滤除基线漂移后的心电信号采用第二组数学形态学滤波模块，此时结构元宽度M为6（图7）。从图8可以看到，第二组数学形态学滤波模块采用结构元宽度M为6对去除基线漂移后的心电信号进行去噪，虽然基本能够去除高频噪声，但是还是有部分宽度较大的噪声不能去除。改变第二组数学形态学滤波模块结构元宽度，加大结构元宽度令M=15，高频噪声去除效果良好，但是形态学滤波器在处理高频干扰时产生了一种近似矩形或梯形的小波动，使得ECG信号在高频小信号范围内产生了失真。

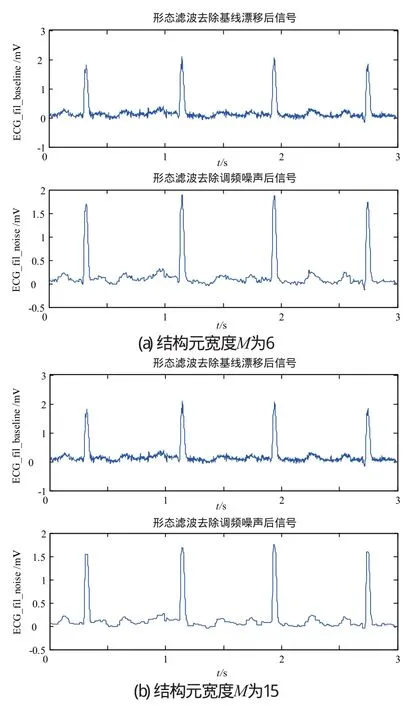
图7 形态学滤波去除心电图信号高频噪声效果

2 综合滤波算法及实验结果

实验结果表明，FIR平滑滤波器算法在处理高频干扰信号时，有很好的处理效果，但无法滤除基线干扰信号。而形态滤波算法在滤除基线干扰信号时，有较好的效果，但在滤除高频干扰信号时，则会产生截断误差。本文将这两种滤波算法相结合，提出了基于FIR平滑滤波器法与数学形态学滤波法相结合的综合滤波算法。该算法首先用FIR平滑滤波器对心电信号进行处理，去除50 Hz工频及其高频谐波，同时抑制频率大于100 Hz的高频噪声，获得了去除工频高频和高频噪声的输出信号，然后采用上一节设计的数学形态学滤波器滤除基线漂移，并进一步滤除高频噪声，该算法流程见图8。

图8 综合滤波处理算法流程图

采用上述综合滤波算法，在对PTB标准心电数据库中的s0001_re.dat的第I导联的部分心电信号数据进行滤波实验。运用综合滤波处理算法后的对ECG信号进行滤波，滤波效果比单独采用FIR平滑滤波器或数学形态学滤波器好。从实验结果比较可以看到，该算法不仅能够去除基线漂移、50Hz工频及其高频谐波，同时可以把宽度很小的噪声滤除，且不会产生了近似矩形或梯形的小波动，出现高频小信号失真（图9）。

图9 综合滤波算法处理结果

3 结论

本文从理论上论述了FIR平滑滤波和数学形态学应用于心电信号预处理的优缺点，并综合两者的优点，提出综合滤波算法，该算法能有效地滤波工频及其高频谐波、基线漂移和其他高频噪声。

[1]王坚,许小汉.一种基于自适应的新滤波技术[J].北京生物医学工程,1999,(3）：10-13.

[2]Agante PM,Marques de Sa JP.ECG noise filtering using wavelets w ith soft-thresholding methods[C].Proceeding of Computers in Cardiology,1999,26：535-538.

[3]季虎,孙即祥,毛玲.基于小波变换和形态学运算的ECG自适应滤波算法[J].信号处理,2006,22(3）：333-337.

[4]Xue Q,Hu YH,Tompkins W J.Neural-network-based adaptive matched filtering for QRS detection[J].IEEE Trans Biomed Eng,1992,39(4）：317-329.

[5]Wariar R.Inter-coefficient bandpass filter for the simultaneous removal of baseline wander,50Hz and 100Hz interference from the ECG[J].Med Biol Eng Comput,1991,29(3）：333-336.

[6]耿向南.基于排列熵的室性心律失常检测算法[J].中国医疗设备,2013,28(7）：17-19,37.

[7]胡广书.数字信号处理[M].北京：清华大学出版社,2003.

[8]Gonzalez RC,W oods RE.数字图像处理[M].北京：电子工业出版社,2007.

ECG Signals Pre-Processing Based on FIR Filtering and M athem atical M orphology

ZHENG Xiu-yu, LU Rui-xiang
Medical Equipment Laboratory, Shenzhen Academ yo
f M etrology and Quality Inspection, Shenzhen Guangdong 518055, China

According to power-line interference and baseline wander of ECG (Electrocardiogram）signals, a composed fi ltering method was proposed in this paper. A simple FIR (Finite Impulse Response）filter was used to elim inate the 50 Hz and high frequency harmonic power-line interference noise in ECG signals, and the baseline wander was removed by using a mathematical morphology filter. Test results showed that the composed fi ltering method proposed in this paper could elim inate the power-line interference and baseline wander of ECG signals effectively.

electrocardiogram signals；mathematical morphology；fi nite impulse response fi lter

TP391

A

10.3969/j.issn.1674-1633.2015.09.005

1674-1633(2015）09-0020-04

2015-07-09

2015-07-20

深圳市科技计划项目（SY200806300171A）；国家质量监督检验检疫总局科技计划项目（2009QK323）。

卢瑞祥，高级工程师。

通讯作者邮箱：luruixiang@126.com