林家有翘楚——中国科学院外籍院士林家翘

文 郭 梅

林家有翘楚

——中国科学院外籍院士林家翘

文 郭 梅

林家翘，力学家和数学家。1941年获加拿大多伦多大学硕士学位。1944年获美国加州理工学院博士学位。1953年迄今历任美国麻省理工学院数学教授、学院教授、荣誉退休教授。美国艺术和科学院院士(1951年），美国国家科学院院士(1962年），台湾“中央研究院”院士(1960年）。林家翘教授是当代应用数学学派的领路人。他在20世纪40年代开始的流体力学流动稳定性和湍流理论方面的工作，成功地解决了已争论几十年之久的两个平行平板间的流动稳定性问题，并带动了整整一代人在这一领域的研究探索。从20世纪60年代开始，他进入天体物理的研究领域，开创了星系螺旋结构的密度波理论，解释了星系旋涡结构的持续和旋臂缠绕等长期悬而未决的困难问题，推动了星系动力学的发展，并为国际学术界所公认。他在应用数学领域做出了多方面的重要贡献，特别是发展了WKBJ方法。1994年，当选为中国科学院外籍院士。著有《流体动力学稳定性理论》《应用到自然科学中的确定性问题的数学》《湍流的统计理论》等。

名门之后

说起林家翘(英文用名LinChia—Chiao，常被称为c.c.lin)，非相关学术领域的人恐怕很少知其名。但说起20世纪30年代清华“四大名将”——彭桓武、王竹溪、林家翘和杨振宁，我们就会发现林家翘列名其中，与杨振宁等并称。

林家翘，祖籍福建闽侯，一个位于福建省东部，福建最靠近省会城市的一个县。不过林家翘父辈很早就到了北京，而他则于1916年7月7日出生于北京，也是在北京长大的，没有回过福建。其父林凯是清末、民国初年于铁道部工作的交通部官员，属于文职人员而非技术人员。他的伯父林旭是“戊戌六君子”之一。

林凯英年早逝，抚养林家翘的任务就全落在了母亲邓氏的肩上。幼年林家翘在家中受教育，可见亦师亦母的邓氏对于林的早期影响是相当大的，然而她的资料却被淹没在时间的长河里——目前，后人只能通过一些其他文献知道林母邓氏是教育家邓萃英的妹妹。

邓萃英与林觉民等人一起参加同盟会，曾担任东京同盟会福建支部长。后又到美国哥伦比亚师范学院深造。辛亥革命后回闽执教，任福州师范学校校长。民国九年(1920年)任北京师范大学校长，民国十九年又为福建厦门大学校长，之后担任河南大学校长。他还担任过福建省督学、教育厅科长、教育部首席参事、次长、河南省政府委员兼教育厅长等行政职务。赴台湾后仍从事教育工作，被推崇为“当代儒宗”和“新闻学”的代表人物。由此可以想见，作为母亲，邓氏的学问也绝不一般，对林家翘早年的启蒙有很大的作用。

师从周培源

林家翘中学时就读于四存中学，然后转入北师大附中，那里有许多高水平的教师。化学教师是一位硕士，物理教师姓方，对林家翘影响很大。1933年中学毕业时，原想读哲学，但家人劝说：“哲学太空泛”，“要想格物致知，还是学物理。”这也与当时实业救国等思想相一致的。于是，21岁的林家翘以第一名的成绩考入清华大学物理系。

20世纪30年代的清华园只是一个方圆几百米的小学堂，但这里却汇集了一大批从海外留学归国的著名学者，大师辈出，人才济济。当时林家翘所在的物理系尤其繁荣，名师很多。近代著名物理学家叶企孙、周培源和吴有训等人都曾经是林家翘的老师。系主任是叶企孙，讲授普通物理的是编写中国第一本《物理学》大学教科书的萨本栋，其他著名教授还有周培源、吴有训、赵忠尧等，讲授课程内容完全能跟上时代。后来，王竹溪讲授统计力学，吴大猷教量子力学，都具有很高的水平。数学方面则有熊庆来、杨武之、赵访熊、曾远荣等名师。

在清华时，周培源、王竹溪、任之恭教授对林家翘都有较大的影响。在所有的老师中，对林家翘影响最深最广的，是后来被称为中国应用数学鼻祖的周培源先生。

林家翘初闻周培源先生的大名，是在大一的时候。1935年秋季，他第一次听了周先生的课。周先生讲课，非常认真、起劲，说话也相当快，听课的学生很受鼓舞。那时候的物理课本都是英文的，大家都必须用中英文记笔记——那时候，多半的物理名词还没有标准的中文译名。每周都有习题，学生看笔记和习题就可以知道是否学会了。

但是，好景不长，林家翘所喜爱的力学课并没有能正常结束，因为学校发生了抗日罢课风潮——那时候的青年，抗日情绪非常之高，“一二·九”、“一二·一六”两次大游行，就是那个学期发生的。汉密尔顿力学（Hamiltonian Mechanics），这门课的最后一部分是林家翘他们自学的。所以，林先生一直感到遗憾的就是没有听到周先生讲汉密尔顿力学。

1937年，林家翘从清华大学物理系毕业。时值抗日战争爆发，他就跟着清华大学的师生一起搬到长沙。清华与北大、南开三校成立长沙临时大学，接着，在1938年春，三校在昆明成立西南联合大学。林家翘他们到昆明那天，正好是2月底，下了40年来的第一次小雪。林家翘是以清华助教的资格随同学校迁移的，所以一方面工作，一方面听些研究院的课程。

在西南联大，林家翘毕业后留校，担任无线电研究所的助教。无线电研究所是林家翘的老师任之恭先生创办的，所以他当时就被送到无线电研究所去当助教。当时刚刚从美国加州理工学院获得博士学位的孟昭英先生从国外回来后被清华大学聘为无线电研究所的教授。因为当时孟先生的家眷还没有到校，所以他就和林家翘一起住在清华无线电研究所的宿舍里。林教授曾回忆说，当时自己是个小学生，孟先生是大教授，感觉到他是个非常脚踏实地的人，这一点给他的印象很深。

青年林家翘

热衷于待在实验室里的孟先生，强调学生的实际动手能力和实验技能。林家翘在无线电研究所做助研工作的时候，发现自己的强项并不在于做实验。对此，他有些苦恼。周培源先生和任之恭先生是非常要好的朋友，在了解到林家翘的这个情况后，周培源先生就向任先生建议，不如把林家翘调回到物理系做助教，由他来指导其做研究。

这样，林家翘就离开了无线电研究所，到物理系做助教，跟周先生学习流体力学，从王竹溪先生学习统计力学。王先生也是周先生的学生，刚从英国剑桥大学R．H．傅勒（R．H．Fowler）门下回国。后来，林家翘也跟他们做些研究，学了不少东西。在这期间，林家翘又听了周先生的普通相对论（包括宇宙论）课程，还听了吴大酞先生讲量子力学，开始了在物理方面的科学研究生涯。1939年，林家翘在《中国物理杂志》上发表了一篇关于统计力学的论文。

留学加拿大

1939年7月，中英庚款第七届公费留学生招生委员会同时在上海、昆明、重庆三地招考，招生名额20名，报考者逾3000。英国是美国之后庚款助学做得最好的国家。与庚款留美不同，庚款留英的宗旨是要为中国科学教育培养出一批高端专家学者，所以留英考试是所有留学考试中难度最大，竞争最激烈的。还在昆明西南联大的林家翘参加了这次考试。他以物理系毕业生资格报考力学专业，注明重点是应用数学。该专业原拟录取弹性力学、流体力学各一名，共两人。但是，林家翘、钱伟长和郭永怀考出了相同的分数，并列第一。因此，原清华、北大的理学院院长叶企孙、饶毓泰决定破例同时予以录取。于是，这届庚款留学生共21人。

中英庚款委员会按照周培源先生的意思，是想用英庚款培养中国航空工业的人才，林家翘要被送到英国剑桥大学，他的导师也已拟定为英国著名流体力学家和应用数学家G．L．泰勒（Taylor）。可是，正当1939年秋，林家翘他们获准赴英，经越南海防抵香港之时，恰逢英国对德国宣战，赴英的海路被封锁了，他们只得折回昆明。

此后，由于英国学者多已疏散到加拿大，中英庚款董事会听从专业教授的意见，经多方磋商，在12月决定此届留英学生可改赴英属自治领地加拿大。于是，这21名庚款留学生又从云南经香港到达上海。

翌年1月，这些留学生登上远洋轮船后，拿到护照一看，才发现护照上有日本领事的签证。大家马上想到：“日本鬼子正在我们的国土上烧杀掠抢，日本是敌国，我们怎能要敌人的签证？”他们七嘴八舌地说：“这不行！我们宁可不去留学，也不要敌人的签证！”“对！我们要有志气，不去了！”于是，林家翘他们立刻把行李扛下船，全部回了旅馆。经办此事的英国人大为恼火，气冲冲地说：“我为你们办理日本领事的签证完全是一片好心，这样你们不仅可以方便地经过日本海，而且船靠横滨，还可以上岸玩玩。”他的好心被愤怒的学生们拒绝了。那个英国人恼怒地威胁道：“遗憾，遗憾！你们会后悔的。”大家的答复是：“后悔？不会的，我们是中国人，我们要维护中国人的尊严！”

1940年6月，庚款委员会再次通知这些留学生经上海出国，当然，改用了新护照。8月，他们搭“俄国皇后”号邮轮抵达加拿大，林家翘和钱伟长、郭永怀一起进入多伦多大学学习。

师从辛格、冯·卡门

在多伦多大学(University of Toronto)，林家翘他们跟随应用数学大师J．K．辛格(Synge) 学习数学物理，研究流体力学。林家翘在多伦多大学虽只待了一年，但受他的导师辛格的影响却不小。当时，爱尔兰人辛格教授是那里的应用数学系系主任，他是剑桥大学出身的，第二次大战后回到爱尔兰的都伯林高等研究所，致力于相对论的研究。1940年，林家翘曾和辛格一起研究湍流。辛格对湍流及流体不稳定性很感兴趣，这对后来林家翘研究不稳定问题颇有启迪作用。他们曾在1940年联合发表《关于各向同性湍流的统计模型》的论文。

1941年，林家翘获多伦多大学应用数学硕士学位，随即转学到美国加利福尼亚理工学院读博士，随世界第一流的流体力学业与航空工程大师冯·卡门（von Karman）研究流体动力学稳定性和湍流问题。辛格与冯·卡门是完全不同的学者，辛格偏重于纯理论及比较严格的数学，而冯·卡门则注重物理现象，比较偏重于实际的应用，但两人毫无疑问都是当时顶尖的学者。冯·卡门是美国航空工程界的首席领导人，同时也是应用数学及力学界的大师。在人才济济的加州理工冯·卡门实验室，林家翘这位华人弟子成绩非常突出，他撰写了一系列关于应用数学在航空学领域的研究论文，在美国应用数学领域的地位不断抬升。冯·卡门交给林先生的博士论文课题就是世界有名的一个多年有争议的课题。1944年，林家翘获航空学博士学位，博士论文题目是《关于湍流的发展》。

冯·卡门有一位密友叫John Von Neumann，是近代最有名的应用数学大师、美国原子能委员会委员，他在应用数学领域有多方面的贡献。就在林家翘先生毕业的那一天，冯·卡门请林家翘和John Von Neumann一起吃饭，将这位著名的应用数学家介绍给林家翘，希望他们之间能进行合作。后来，John Von Neumann就领导一组有名的学者，证实了林先生的研究结果，结束了学术界这一多年的疑案。当时林家翘做的这一课题是一块难啃的硬骨头，林家翘通过自己的研究，证明了海森堡的研究结果基本是对的。于是，海森堡就写信给他的导师，说一位中国人证明了他的研究结果。为此，1946年，当时年仅30岁的林家翘获得了美国麻省理工学院副教授的职位。

这之后，林家翘继续在湍流理论研究方面进行探索，没想到在研究过程中与一位瑞典力学家各执一词，相同的问题研究结果却相去甚远，这位瑞典力学家为此在一次与别人的争执中得脑中风而亡。林先生在他去世前曾去医院看望他，对他讲，复杂的问题自然会有争议，不是你研究的结果与我的不一样你就不对，其实两人都对，复杂问题是多方面的，不同的研究结果可以应用到不同方面。他们这一学术理念最后变成了一个大题目——复杂性。有一个杂志专门取名为《复杂性》，探讨此类问题。

林家翘从加州理工学院毕业后，曾任工程师留校工作一年。1945年“二战”结束，所有的人都要各奔前程了。该年11月，林家翘就离开帕萨迪那，到布朗大学数学系的应用数学部任助理教授。在第二次世界大战中，布朗大学因承担应用数学及国际课题而著称，各国的许多名教授聚集在此。1947年，布朗大学已打算聘林家翘为正教授，不料美国最著名的学府之一，麻省理工学院(MIT)也聘他为副教授。经过权衡，林家翘去了麻省理工学院。1953年，林家翘成为麻省理工学院的正教授。1966年，林先生被选入美国科学院院士，也成为 MIT的学院教授（Institute Professor）。从1947年到如今，林家翘已在波士顿的这所著名学府度过了40多个春秋。

挑战争议

物理学认为，不稳定性就会使流体流动从层流转挟成湍流，而自然界的流动大多是湍流，所以从层流转挟到湍流，成了物理学家关注的大问题，一度是物理学上的悬案。

传说，德国著名物理学家So~erfeld在1920年左右曾经说过：“我只指望在我去世前，有人能告诉我量子力学的秘密。”有学生和同事就问他：“那湍流的问题呢?”So~erfeld教授答道:“那只有等待圣彼德(st.Peters)在我上天堂时告诉我了。”可见湍流问题在物理学大师心目中的地位。后来Heisen-berg(海森堡)来了，Sommerfeld认为这个年轻人够聪明了，就要他去做湍流的研究，结果Heisenberg就成功地解出了Orr-sommerfeld方程。Orr-sommerfeld方程就是解决这个问题的关键，但是海森堡做出的结果有争议，平行流的不稳定性问题还是没有解决。

海森堡（Werner Heisenberg）

在1924年写的博士论文中，考虑介于两平行板之间的二维流动，原始速度为W(y)，然后加上扰动，则其速度分量为：

海森堡运用对α作渐近展开的方法指出，当R→∞时α→0，这时能求出流体运动稳定与否的分界。

海森堡的这篇论文发表之后，受到许多批评，因为有两个重要问题未解决——

从教学上看，他没有论证2R≥1的渐近展开是否正确，更谈不上给予严格的数学根据。

曲线没有作定量分析，获得精密数值结果，而仅对其中一枝作了粗略计算；另一枝的估算，则只是根据他对有关R的下限和α的上限所作的猜想。数学家F·诺特(Noether)曾说，像这样的曲线——标志稳定区域的中性曲线也许根本不存在。因此，更多的人对海森堡的论证待保留态度，以致这一有关平行板之间流体稳定性问题的研究成了一件多年悬案。

林家翘先生当时在著名的加州理工大学，经周培源先生推荐在世界导弹之父冯·卡门的门下攻读博士。这位美籍犹太科学家，是林家翘接触的第一位世界级大师。他给了林家翘一个很好的论文题目，就是海森堡的论文题目。

林家翘发现，其实 Orr-Sommerfeld的四个解，海森堡都已经找到了，只是他没有进一步去解那个本征值问题。于是，他就使用Heisenberg的4个解，加上正确地运用了边界条件，解决了这个本征值问题，成功地解释了为什么黏性会使流体的流动从层流变成湍流——林先生不仅从数学上完整地解决了Orr-sommerfeld方程的本征值问题，而且从物理上说明了流体的黏性可以稳定流动，也可以成为制造不稳定的诱因，它具有两重性，所以具有拋物线速度剖面的平行流动，在 Rayleigh的无黏流体的稳定性定律下是稳定的，而当计及流体黏性后，就可能不稳定，并为实验所证实。

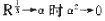
林家翘的论文发表之后，引起了新的争论。普林斯顿高级研究院的C．L．派克里斯(Pekeris)通过不同的渐近方法指出，抛物流很可能是完全稳定的，不存在稳定区域和不稳定区域的中性分界线，这恰和上述诺特的结论相吻合。这是1948年的事。两年之后，国际数学家大会在美国波士顿的坎布里奇举行。海森堡在大会上作了“层流的稳定性”的报告，肯定了林家翘的结果，并断言诺特的论文中必定含有某种错误，只是尚未被发现而已。因此，到1950年为止，此争论还在继续。

又过了两年，L．H．托马斯(Thomas)按照冯·诺依曼(von Neumann)的建议，对抛物流情形下的文程(2)的解的速度c的虚数部分，到IBM电子计算机上工作了150小时，结果证明海森堡和林家翘的结果是正确的。巽友正 (Tatsumi Tomomasa)也对派克里斯和林家翘的结果重新作了检查，仍然证实林家翘的工作是正确的。

1955年，英国剑桥大学出版社推出林家翘的专著《流体动力稳定性理论》(The theory of hydrodynamic stability)，成为流体稳定性和湍流发展的里程碑式的著作。从此，林先生在流体力学界有了个雅号“不稳定先生” (Mr.Instability)，但是认识他的人都称他“CC”。

1958年，苏联将它译成俄文出版。林家翘在这本书中发展了二维不可压缩流体的稳定性理论，给出了精到的数学阐述，曾是一个时期的典范。它不仅是理论成果，还是许多应用科学的基础，对实用工程技术、地球物理学、天体物理学等都产生了深远的影响。林家翘的这一工作，引起力学界和数学界的高度评价，更有许多人继续推进，加以简化。1982年，剑桥大学出版社出版了第二部关于不稳定性问题的著作。

海森堡论文留下的悬案中的第一个问题纯数学问题，即微分方程在转向点附近一致有效渐近解的性质及形式。此类问题在量子力学的薛定语(Schrōdinger)方程中早已出现。一种较简单的数学基础是R．E．朗格(Lange)所提供的，朗格曾用他的方法来研究方程(1)和(2)，但未能成功。林家翘基于1944年所作的力学分析的先驱性成果，与他的学生A．L．拉本斯坦(Rabenstein)于1958年证明了一系列的数学定理，从数学上彻底解决了这一悬案。他们的最早论文发表于1960年。

林家翘成功地证明这一系列定理，发展了常微分方程的渐近解理论，不仅在力学界、应用数学界赢得广泛声誉，而且在理论数学界受到赞扬和敬重。后来，林家翘能在麻省理工学院的纯粹数学系设立应用数学委员会，发展应用数学，与此不无关系。

林家翘在讲解星系螺旋密度波理论

转探天体

20世纪60年代，林家翘将近代力学中提炼模型的方法用于研究天体物理，提出准稳旋涡结构假说，创立星系旋涡结构的密度波理论，并用它解释天文观测事实，成功地解决了星系悬臂研究中的一些难题，促进星系动力学的发展。

林家翘先生成名的研究工作是平行流的不稳定性理论，那他为什么会改变研究方向，转而去做天体物理学研究呢？

由于林家翘上述纯数学工作发展了朗格的研究成果，朗格遂于1958年邀请林家翘到威斯康辛大学讲学——此行对林家翘以后几十年的工作有极大的影响。当时，普林斯顿高级研究院(Princeton Institute for advanced studies)的物理学家杨振宁恰巧也在威斯康辛大学访问。杨振宁先生正在研究玻色-爱因斯坦(Bose-Einsteim)凝聚问题，凝聚产生了超流体(superfluid)，需要一个既懂物理学又精通流体力学的人帮忙，而林家翘先生无疑是最理想的人选。杨振宁先生就请他的学长林家翘先生去普林斯顿高等研究院访问一年。1959年秋，林家翘到达普林斯顿高级研究院。

就在这一时期，通过杨先生的介绍，林先生认识了在高等研究院的一位杰出天文学家斯特龙根(BengtStromgren)。斯特龙根是丹麦人，在天体物理学界很有地位，在星球外围有一个电离的球状区域，就叫斯特龙根球体(Stromgrensphere)。有一次，斯特龙根邀林先生去参加一个天文学学术会议，在会上，林先生听到星系较差自转及著名的旋紧矛盾的问题，就是说星系中心转得很快，按这个方式去转，星系的旋臂将在很短的时间就转成了一个绒线团一样的形状，而星系已经存活的时间已远超过这个旋臂旋紧所需的时间，而有可见的螺旋星系，旋臂都是很开放，完全没有被旋紧的，天文学家叫这个现象为旋紧矛盾(windingdillemna)。面对这个天文学上有名的大问题，林先生马上就认识到这些旋臂一定不是同一物质组成的，而是一个密度波。他随即去寻求问题的近似解，发现螺旋密度波是一可以满足流体力学方程的解，接着，他就着手建立了更严谨的螺旋密度波理论——他和他的学生徐遐生撰写了《关于盘状星系的游涡结构》，乃是这一领域的先驱性工作。他们随后又发表了一系列的论文，逐步形成了独特的旋涡星系密度波的现代理论，引起天文学界的广泛重视。徐遐生后来在加州大学（柏克利）任天文系教授，并于1993年当选为美国天文学会会长。

林家翘先生对物理的理解之透彻令人叹服。他常常说物理是一个实验科学，天体物理学不能做实验，就要靠观测。因此他对观测的结果非常熟悉，而且不断地去寻找新的结果。

密度波理论对天文观测的专家是有一些难度的。如果要使密度波的理论在天文界具有影响力，一定要分析他们的观测结果，用理论与他们观测结果做一对一的比较，才能赢得他们的支持。但是，这个工作不好做，因为星系螺旋密度波不像水波能看到它在水面上传播，螺旋密度波是绕着星系中央旋转的，其转速非常之慢，以银河系为例，转一整圈需要5亿年，再精确的望远镜也别指望能看到螺旋波的转动。所以，一定要用旁证的方法，就是找出密度波可以产生也可以观测到的一些现象，这就包括了光学、电磁波、红外线、磁场的各种观测。而其中一个最重要的数字，就是螺旋密度波的旋转角转速度。林先生与他的高徒们用了各种方法，以银河系为对象，去找这个螺旋式样的角转速度(又称型式速度patternspeed)。

当时的台湾中研院天文研究所教授袁旗跟随林家翘先生做天体物理学研究，据他回忆，在这个过程中，林先生作为优秀学者的风范深深影响了他——

第一，从不轻言放弃。当时我在做星球迁栖(starmigration)问题，开始时结果不是很好，因为星球的年龄很难准确地定出，我有些灰心，林先生说是星龄的问题，要持续做下去，果然调节了星龄，结果就改变了，就做成功了。

1978年7月，邓小平会见林家翘和夫人梁守瀛

第二，非常注重结果的陈述(presentatioil)。中国学生一般不懂这个道理，很好的结果显示得了了无奇，不是很出色的结果，就更不用说了，林先生非常讲究结果的表达，我做了又做，直到他满意为止。

第三，敢下结论。我最初做出的银河系密度波之型式速度是12.5km/sec一kPc，是太阳绕银河中心旋转角速度之一半，这个结果是由星球迁栖研究得出来的，但是把它代入林一徐色散关系(Lin一HsuSta:dis-persionrelation)时，银河系中的螺旋就会转得比较紧，因此太阳附近的猎户星座旋臂(Orionarm)就难放入这的螺旋型式了，林先生马上就决定猎户星座旋臂不是银河系的主要旋臂，而是旋臂之间的一个枝节(sPur)，这一个看法的提出，十分具有革命性。从1969年以迄今日已经近40年了，这一看法已经被天文界普遍采纳了，一直到今天，我还不知道他怎样能下出这样一个既大胆又有创见的结论。

第四，有远见。在各种混乱的观测数据中，率先地去定出螺旋密度波的型式速，是林先生战略的成功，这一型式速度的决定奠定了密度波理论的地位，这是事先不可预料的，也是林先生洞悉物理学才能有此远见，因为有了这个型式速就解决了双激波的形成问题，从而解决了为什么螺旋旋臂被明亮的新星点缀而成的著名问题。当时哥伦比亚大学的Pordengert教授与藤本(Fugimoto)博士也在做这个问题，就是因为型式速度不对而没有找出答案。

第五，公正。就是说决不抢人家的研究成果，任何一篇文章，林先生总是会把他人的研究结果公平地归于其创造者，决不疏忽，甚至他一再把密度波的创始归功于B.Lindblad。其实Lindblad教授1959年提出的密度波，其实是非常粗略、原始，决不是林先生精心构建、演绎出来的理论。星系螺旋密度波理论在天文界起了震憾的作用，1970年在英国召开的第14届国际天文学会大会上，林先生被请去作大会邀请讲演(inviteddiscoulse)，这是天文界的殊荣，我和徐遐生也都参加这个盛会。

当时林先生名满天下，歧见随之，在MIT就有一位Toolnre教授对密度波提出了反驳，认为被螺旋密度波覆盖的星系盘应在很短的时间内(与宇宙历史相比)消失，所以我们看到的星系上的螺旋结构应该不是密度波。面对这一异议，林先生非常冷静，立刻用驻波(standingwaves)的概念进行反驳，这也是非常有见地的对策。后来，他与几位新来的年轻人Y.Y.Lau、JamesMark、G.Bertin等把这个概念用数学物理的框架建立了起来，并完整地发展成理论。

可见，在林家翘先生温文儒雅的外表下，他是如此的强韧，如此的具有竞争力。

责任编辑/胡仰曦