防止“忽略” 提高教学实效
2015-05-30周晓芳
周晓芳
【摘要】 纵观现如今的初中数学教学,学生的数学水平差异很大,除了一些共性的原因以外,还有一些细节的方面往往被我们所忽略,没有去重视,导致学生在学习能力上的生成性、课堂教学的有效性无法达到我们预期的目标. 针对“忽略”现象我们该如何应对,我们又该如何避免“忽略”现象的产生,是本文所要研究的重点.
【关键词】 课堂教学;忽略现象;问题;思维
新的数学课程标准提出:在数学课堂教学中,教师应遵循课改精神,实施以科学探究、学生为主的多样化、多元化的教学方式. 课堂教学中,教师应着重于培养和发展学生的创新意识和实践能力,从而全面提高学生的数学素养. 教学中教师也应更多地采用以全面促进学生数学思维的教学手段,可能每个“一线”教师都会有这样的经历,虽然在课前有时觉得自己准备很充分,但在具体教学过程中还是会存在一些问题,譬如“忽略”现象,使得课堂教学有时并不能收到预期目标.
一、如何界定“忽略”现象
“忽略”,顾名思义,它为“忽视、简略”的意思. 在多年的实践教学中,本人浅意地把“忽略”定义为数学教学中教师与学生的互相“错过”,教师忽略了学生的“动手、动脑”等思维,学生忽略了教师讲解的要领、深义,等等. 可以说,它在课堂教学中会偶尔出现(其实偶然中显现了必然),可若真正被“忽略”了,那就会时不时地经常出现,那偶然也就成了必然了,长此以往的话,后果将不堪设想.
二、为什么会“忽略”
在数学教学中,“忽略”现象屡见不鲜,主要有以下几个原因:
1. 学生的主体思维及其主体作用没有受到教师足够的重视. 在课堂教学中,教师提出问题后没有给学生留下足够的思维空间,很多教师为了赶进度,总是自问自答,学生“知疑——思疑——释疑”的自主思考过程自然而然就被“忽略”了. 例如,在讲方程概念时,教师都会直接地告知学生方程的概念,但是几乎还没有学生知道什么等式. 更为突出的例子有:教授一元二次方程根的判别式时,不少教师都会提出这样的问题:一元二次方程根的情况是由谁决定的?紧接着就把问题点破,把结论和盘托出,这些都无疑在不经意中剥夺了学生主动思考、主动探究的主体权. 这种“忽略”现象的产生其实完全可以避免. 倘若教师在提出问题后出示一些针对性的问题、习题等,让学生通过自己的探究、计算或分析、推理、总结等,结论说不定也同样出来,当然也许学生的见解不一定完全正确,但它毕竟是学生主体参与的成果,即使是错误的也能让学生加深对知识的正确认识和理解掌握.
2. 教师在备课时对问题已经备选了一个或几个解决方案,课堂上却以“定式思维”组织教学,当学生的思路与预设方案相左时,教师或因学生的想法不切实际,或因不愿打乱既定的教学计划,或因本能的排他性而对学生的想法不做认真的分析便予以回避甚至进行比较武断的评判,这既伤害了学生的自尊心,也使得一些可能有探索价值的问题轻易地被“忽略”掉了. 如下题:
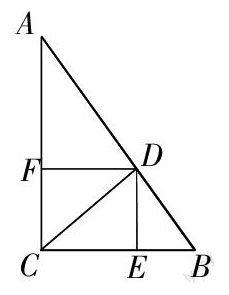
已知:如图,△ABC中,∠ACB = 90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E,F. 求证: 四边形CFDE是正方形.
分析:一般学生都会联想先证明矩形后证明一组相邻的边相等. 实践中发现学生通过全等证CF = CE,或者通过证∠ECD = ∠EDC = 45°,而后得到ED = EC. 很少有学生去联想角平分线的性质证明DE = DF. 如果教师因学生没提及而就把这种方法忽略掉了,那么对以后的相关证明无疑是一大损失,因为它恰恰是值得我们教师去锻炼培养学生发散思维的极佳题目.
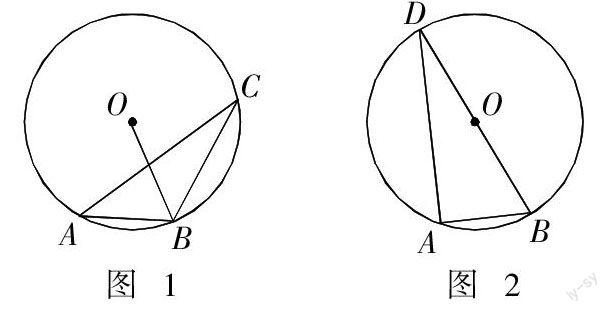
又如,A,B,C为⊙O上的三点,AB等于圆的半径,求∠BCA的度数.
一般的解法(图1):连接OA,OB,求出∠AOB,然后再利用同弧所对的圆周角和圆心角的关系求出∠BCA;而当学生提出∠ADB的度数就是∠BCA的度数时(图2),老师不及时给予答复,所产生的不良影响后果是可以预见的,因为这恰恰是非常值得探讨的解法.
3. 问题梯度、广度设置不合理. 梯度过小容易使学生产生思维惰性,广度过大又容易导致思维空洞或卡壳. 在这些情况下,往往使学生的思维活动因不能深入进行而流于形式,造成事实上的“忽略”. 譬如在学习正方形的性质与判定时,教师可以与学生一起在温习平行四边形、矩形、菱形的情况下,循序渐进地导入学生想往的“正方形”境界. 试想:教师直接发问:什么是正方形?学生“七嘴八舌”,可谓答案繁多. 笔者在不同的两个班实践了不同的问题启发,正如前面描述的情况,一个班级学生井然有序地回答了概念与性质,而直接发问的另一个班,学生就糊里糊涂地“探究”起来,最终还是茫然也没个确切的说法. 反思一下:可谓问题的指向性不够明确了,依学生的能力回答这样科学性的问题怎么会不感到吃力?若教师加上梯度、广度适当的四边形流程图复习问题,学生就会豁然开朗,思维明晰了.
4. 学生“从众”心理的简单思想“作怪”,懒于挖掘,懒于深究,可谓创新思维意识淡漠,能力缺失. 因传统教学使学生形成了因果必然、结构严谨、循序渐进的经典问题解决模式,思维囿于固有的定式之内,养成唯书、唯师的惰性心态,从而导致课堂学生“忽略”教师“深意”现象的发生. 如:在针对中考做综合性复习时,教师所给出的例题与习题偶有差异时,好多学生是选择放弃,这种学生“忽略”老师的现象其实屡有发生. 笔者认为这不仅仅是学生自身知识不足的体现,多年的实践告诉我们,学生好多时候在玩“忽略”. 教师不得不重视这一现象.
三、如何防止“忽略”
教学中的“忽略”现象,如果不作为问题提出来,可能不会引起我们的注意,因为它表面上看起来是在无意的情况下发生的,具有一定的偶然性和不可避免性,实则不然. 偶然性的“忽略”现象其实是教师教学观念的必然反映,所以,要想避免“忽略”现象的发生就必须改革“教”与“学”的传统观念和教学方法.
1. 转变传统“应试”教育观念
应试教育使得课堂教学必须有明确而具体的教学计划、教学目标和教学要求,教师只有按预设的教学程序,创设稳定、规范、整齐划一的教学氛围,使教学过程有一个“好”的开始和“圆满”的结束,才算完成了教学任务. 如果因学生的思维超出了预期的深入性或偏离了预设的轨道而延滞了后续的教学任务,就被认为是一种失败的教学. 如此一味地追求教学的“严谨性”“有序性”和“完整性”,其结果教与学的相互性、学生思维的“开放性”和“自主性”就不能有效地开展,也就不可能辨析歧义、接受质疑、捕捉灵感,“忽略”现象也就在所难免了.
2. 改革传统的教学方法
改革传统的“教大于学”的教学方法,重视问题性教学,重视感悟学习,使“学大于教”,精心创设发挥学生主体作用的条件.
(1)要创设生动活泼的问题情景,自由、合作的教学气氛. 师生一起进入问题情景,彼此之间建立一种积极平等的协作关系,教师要鼓励、引导学生积极提出自己的见解或疑问,使课堂充满智慧,并且不论正确与否,都要进行必要的讨论,给予适当的评价,好的加以肯定并且鼓励其进一步探索、创新,让学生体验到成功的喜悦;对于抓不住问题要点的学生要主动、妥善地加以引导,不惜时地在问题关键处给予点拨,帮助其理清思路;对于出现不当或错误的学生,不能轻视或讥讽嘲笑,抑或置之不理,要采取尊重和鼓励的态度,以保护其思维的积极性.
(2)要科学设置问题,使问题具有:
① 主题指向性. 也就是说问题的内容要有一定的目标,这样才能使学生的思维具有明确的方向,才能集中精力主动地思考问题,不会因为漫无目标的思维或无关紧要的问题而影响和分散精力.
② 广阔开放性. 明确了问题的主题性以后,问题还应具有开放性(开放的设计、开放的思路,甚至开放的结论)让学生从不同层次、不同侧面、不同角度、不同方向对问题进行思考,打破其墨守成规的思维定式,促使他们进行发散性思维,把问题理解得更全面,掌握得更牢固,运用时才会更灵活.
③ 难易适度性. 问题的适度性极为重要,前面谈过问题起点过低或难度过高,都容易导致忽略现象的发生. 因此实际教学过程中,低难度问题可考虑合并提出,高难度问题则进行层次分析,按照思维由浅入深、有简单到复杂的规律设置问题,前为后做铺垫,后为前做深化,引导学生逐步解决目标问题.
④ 内外延伸性. 延伸性是指所预设的问题既构建着当前教学应该解决的问题,又适当蕴含着潜在的与当前教学目标相关的问题,给学生留下课后思考的空间,创设一种意犹未尽的学习环境,使课堂问题具有延伸性,让学生兴趣盎然地循着课堂设计的问题线索去进行课外的学习和思考,以增加自主思维的时间和机会,也可以适当预防“忽略”现象的发生.
(3)要巧妙灵活地引导“探究”,给学生留下足够的思考与探索的空间. 在关键问题和关键环节处,教师不能急于点破,在读一读、想一想、做一做的自主参与中感悟问题,获取知识,体验成功,从而进一步调动其自主学习、深入探究的积极性.
3. 着力培养学生自身的质疑意识和能力
质疑是探索知识、发现问题的开始. 爱因斯坦曾经说过:提出一个问题往往比解决一个问题更重要. 要防止学生方面的“忽略”因素,必须切实提高学生的质疑意识和能力,使其勤于向自我惰性挑战,勇于向从众心理挑战,敢于向老师、教材的权威性挑战,从而善于发现并提出问题. 只有这样,才能使其思维具有主动性、创新性,以减少“忽略”简化现象的发生.
新的课程理念要求我们每一位老师不仅应关注学生学习的整个过程,更应关注学生在学习过程中所反映出来的认知规律及心理发展方面的特点,课堂教学中也更要关注学生的意外“生成”,善待“生成”,由此使我们的教学更具针对性、实效性,从而提高课堂教学的有效性.教师教学中产生的“忽略”现象以及学生学习中产生的“忽略”现象,不仅需要我们去警惕,更值得我们去研究,去思索,并寻找相应的方法去解决应对,唯此才能使教学更具有实效性与高效性,也才能使学生更好地发展.
【参考文献】
[1]周成平.新课程——名师教学100条建议.中国科学技术出版社,2005.
[2]郭思乐.感悟学习的若干思考[J].课程·教材·教法, 2002.
[3]于浩.课堂组织艺术.北京学苑出版社,1999.
[4]马复.义务教育课程标准实验教科书·教师用书(数学7~9年级).北京师范大学出版社,2001.
