人脸关键点检测
2015-05-30章乐
章乐
【摘要】 人脸关键点检测又称脸部关键点定位。在机器学习的领域里,人脸关键点检测技术有着其独特的应用价值,因为该技术是众多脸部图片处理的先序步骤,这些应用包括但不限于人脸识别,脸部表情分析,脸部变形动画。本文尝试了四种不同的机器学习模型来实现人脸关键点的检测,并利用Kaggle数据库对各模型的检测效果进行横向对比。其中卷积神经网络模型拟合效果最好,其Kaggle测试均方根误差仅为3.21。
【关键字】 Kaggle 人脸关键点检测 线性回归 支持向量机 前馈神经网络 卷积神经网络
一、Kaggle数据库简介
Kaggle数据库一共提供了7049张96x96像素的训练灰度图。对于每个样本点,数据库提供15个关键点的x, y坐标(关键点坐标允许部分缺失),即30个训练特征(feature)。对于测试数据集,Kaggle提供了1783脸部灰度图。模型预测坐标将被用于与Kaggle内置的脸部关键点坐标进行比对,其相应的均方根误差(RMSE)为模型得分。
二、线性回归
2.1 线性回归模型存在的问题
对于线性回归模型,9216个像素灰度值将被作为输入特征,而相应的15个人脸关键点(位于眼、鼻、嘴等处)的X,Y坐标将被视为目标变数(variable)。为解决模型的过度拟合问题(overfitting),我们采取了部分特征抽样的方法以减少输入特征。
2.2 特征提取
在给定特征抽样比例时,我们仍需对9216个输入特征进行筛选。分段启发函数(stepwise methods)是一個普适的特征选择方法[1],但随机性过强的分段方法并没有充分考虑脸部关键点坐标间存在的联系 。
与一般机器学习问题不同,关键点定位存在很直观的特征提取启发策略—我们可仅提取眼、鼻、嘴处的像素值。实验中,我们采用了以健壮性著称的方向梯度直方图HOG(Histogram of Oriented Gradients)来探测并截取其对应区域的像素,如图1所示[2]。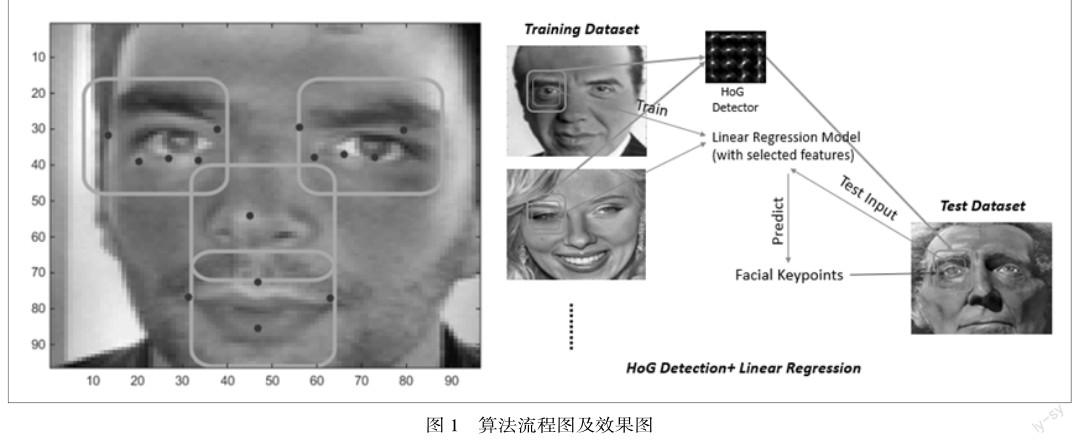
2.3 模型复杂度控制
我们从左右眼、鼻及嘴区域截取了长宽分别是H,W的像素块作为线性回归模型的输入特征,通过调整像素块的大小来控制模型的复杂度。当H与W增大时,模型复杂度随之增加。在实验中我们发现,检验方差及训练方差(Validation and traning MSE)随着像素块的增大而减小。这说明我们得到的线性回归模型仍处于欠拟合区域(Underfitting)。然而,我们无法进一步增大提取像素块,否则像素块边界将会产生越界现象。通过观测,最佳的像素块长宽均为32(像素)。对于该大小的像素块得到的最终线性回归模型,其Kaggle测试均方根误差约为4.6367。
三、 支持向量机(support vector machine)
支持向量机(SVM)是广泛应用于机器学习分类以及回归的抽象模型,因此存在众多成熟的工具包。在实验中,我们采用了著名的LIBSVM [3]来对数据进行拟合。我们利用9216个像素值作为输入特征分别训练30个向量机,每个向量机输出15个脸部关键点的X或Y坐标。这样的简化处理并忽略了坐标间存在的内部联系,却成功避免了引入多目标变数向量机(SVM struct [4]),使代码大为简化。
3.1线性卷积核
对于输入特征较多,训练样本较小的机器学习问题,线性卷积核是一个合理的选择。在LIBSVM工具包中,我们仍需选取合适的正则参数C(regularization parameter)。对于线性卷积核,搜索得到的最佳正则参数C为0.1,其对应模型的方差由默认参数的10.663降至10.454,Kaggle测试均方根误差为4.35512。
3.2 多项式卷积核
对于多项式卷积核的SVM模型,其最重要的调谐参数是多项式的最高次幂。在交叉检验中(Cross-validation),我们发现均方差与多项式核的最高次数呈正相关,即检验均方差从线性核(P=1)时便开始增大,说明多项式卷积核的SVM在P=1时就已经出现了过度拟合的现象。
3.3径向基函数核与参数调谐
由于径向基函数核(Radial Basis Kernel)能够非线性地将输入特征映射到更高维空间,因此它能够处理绝大部分目标参数与输入特征存在非线性关系的机器学习问题。更为巧妙的是,当径向基函数核的惩罚参数C (不同于正则参数)及核参数γ为某一特定组合时,其SVM模型的拟合效果将完全等同于与线性核SVM模型 [5]。逻辑回归卷积核与径向基卷积核SVM也有类似的关系[6]。
四、 前馈神经网络
4.1 基本结构
常见的神经网络(Neural Network)结构包括前馈神经网络(feed-forward),递归神经网络(recurrent)以及对称连通网络(symmetrically connected)等等。在该论文中,我们采用了实际应用较广的前馈神经网络结构。
根据[7]的论述,在给定相同数量的神经元,拥有更深结构的神经网络模型拥有更强的表达能力。因此,一个典型的前馈神经网络应至少包含三个层次-----输入层,输出层以及在这两层之间的隐藏层。对于脸部关键点检测问题,输入层一共有9216个神经元,输出层将由30个神经元组成。
4.2 模型的参数设定
如前所述,神经网络模型复杂度主要取决于隐藏层的层数,每层拥有的神经元个数以及迭代次数(epochs)。在该实验中,我们使用了目前较为先进的机器学习工具包 Theano[http://deeplearning.net/software/theano/]。
4.2.1 隐藏层层数、每层神经元数量及迭代次数的选取
由于特征值域映射问题,Theano的显示误差为均方差的千分之一。由图2知,当层间神经元数量超过300时,交叉检验误差显著上升,模型出现了过度拟合现象。在实际Kaggle测试中,我们尝试了三个不同隐藏层层数(1,2及3层),其对应的均方根误差为3.82109, 3.85388以及3.81652。这一结果显示了隐藏层数的改变并不会对拟合结果有显著的影响。显然,当迭代次数增加时模型复杂度也随之增加。由图2(右)知,迭代次数设置为1000是一个较为合适的选择。
4.3 集成学习4.3.1 Bagging对于神经网络模型,我们可以采取两种不同Bagging策略。
(1)从训练数据中抽样选取部分样本点。我们分别训练了10个不同的神经网络,其输入样本为从训练数据中随机抽取的1940个样本点。最终的脸部关键点坐标取这10个模型预测结果的算术平均值,其Kaggle测试均方根误差为3.67293。
(2)从每个样本点(脸部图片)中选取部分输入特征,每个样本点的输入特征为随机抽取的8000个像素点。相应模型的Kaggle均方根误差为3.62655
4.3.2 混合模型
同样地,我们可以采取如下两种不同的混合策略。
(1)我们分别训练三个仅有1层,2层以及3层隐层的神经网络,并取其预测的脸部关键点坐标算术均值作为预测结果。该模型Kaggle测试均方根误差降至3.62702。
(2)混合由(1)中的神經网络以及Bagging的第二种模型(部分特征抽样)。这两种目前表现最佳的神经网络的结合进一步降低了均方根误差。该模型的测试均方根误差约为3.58884。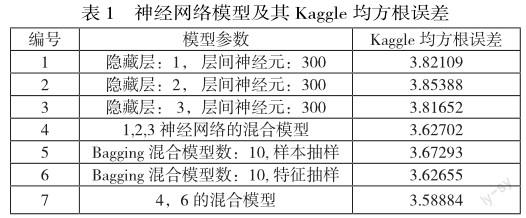

4.4 总结
在论文的本节中,我们尝试了一系列参数各异的神经网络和集成学习模型,使得均方根误差由最初的3.8降至了3.58884。模型及其相应的均方根误差如表1所示。
五、卷积神经网络
5.1 模型结构
卷积神经网络(Convolutional neural networks, CNN)是一种较为新型、直到90年代末才被成熟开发的神经网络结构。在没有牺牲模型的普适性前提下,卷积神经网络有效地利用了局部像素间关联性,缩短了机器学习训练周期。对于卷积神经网络,每一层神经元将构成三维结构(传统神经网络是二维平面结构),而层间的神经元只与前一层的神经网络的局部神经元存在激励、反馈联系,这一特性称为局部感知。
5.2 训练卷积神经网络
在本论文中,我们尝试了一系列参数各异的神经网络模型,并使用NVIDA GTX-650显卡与1GB内存对模型进行训练。在训练过程中,我们将Kaggle提供的训练数据库分成训练数据及检验数据,其规模之比为4:1。
5.2.1 卷积神经网络结构
实验中使用的模型参数:输入层一层,由9216个神经元组成;卷积层(Convolution)及最大值池化层(Max Poolling)各四层,每一层的卷积滤窗大小为3x3,池化过滤窗大小为2x2,位移步长为2。卷积核数从第一层至第四层分别为32, 64, 128以及256;全连通卷积层一层,包含500个隐藏神经元;输出层一层,由30个神经元组成。神经元的激励函数采用的是RELU非线性函数,输出层输出将取决于全连通层激励信号的线性组合。为了提高训练速率,我们将学习速率(training rate)设置为一较大值并随迭代次数线性减小;动量项(momentum)随迭代次数线性增加。为了避免可能的内存问题,斯托克斯数据包大小(stochastic batch size)设定为64. 从图5.1可以看出,上述的改进大大加快了均方差的收敛速度,缩短了训练周期。
5.2.2 数据扩充
对于图片类型数据,我们可以垂直翻转图片实现数据扩充。由于训练数据库规模变大,我们将迭代次数上线由600增至700。
利用数据扩充的策略,从图5.1中可以清晰地看到不仅训练误差明显降低,检验误差也随之下降,意味着卷积神经网络得到正确的优化。
5.2.3 激励摒弃(dropout)
激励摒弃(dropout)是避免过度拟合的又一新型策略,其在卷积神经网络中的应用直到最近几年才被关注并被开发。激励摒弃是在每一卷积层随机选取一定数量的激励神经元,并将其激励人为地置零。对于不同的训练图片,归零的激励神经元也需重新选取。激励摒弃可以有效地抑制神经元间的过强联系。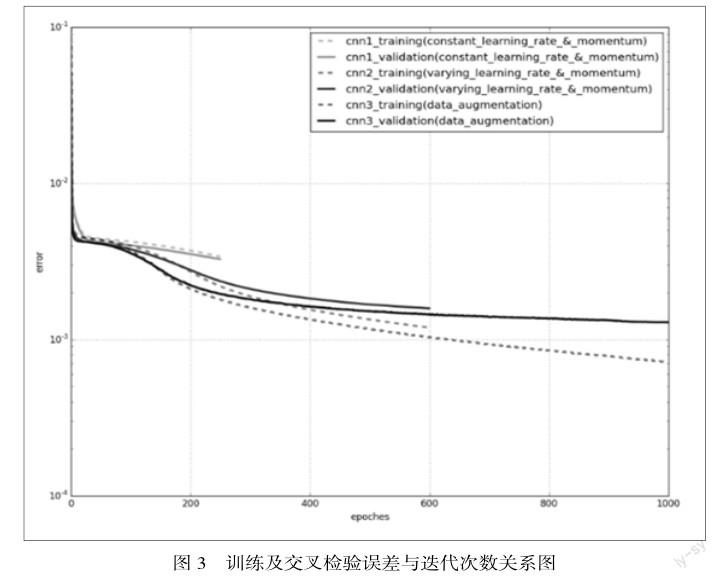
利用激励摒弃的策略,我们将迭代次数增至1000,此时Kaggle测试均方根误差降至3.45;若将迭代次数增3000,其相应的Kaggle均方根误差降至3.21。当我们进一步增大迭代次数时,均方根误差下降已十分缓慢。
六、结语
在本篇论文里,我们尝试了一系列健壮的机器学习模型并系统地比较了他们的拟合效果。由于缺乏有效的特征选取及模型复杂度控制机制,基于计算机视觉的线性回归模型并不能取得很好的效果。
而卷积核的灵活性使得支持向量机SVM在前者的基础上有了明显的进步。然而前馈神经网络以及卷积神经网络能够更为有效地控制了高维模型的复杂度。
其中,专门用于图片机器学习的卷积神经网络在Kaggle的测试中有着极佳的表现,经优化后其均方根误差仅为3.21959。
參 考 文 献
[1] Efroymson, M. A. “Multiple regression analysis.” Mathematical methods for digital computers 1 (1960): 191-203.
[2] Dalal, Navneet, and Bill Triggs. ?Histograms of oriented gradients for human detection.? Computer Vision and Pattern Recognition, 2005. CVPR 2005. IEEE Computer Society Conference on. Vol. 1. IEEE, 2005.
[3] Chang, Chih-Chung, and Chih-Jen Lin. ?LIBSVM: a library for support vector machines.? ACM Transactions on Intelligent Systems and Technology (TIST)2.3 (2011): 27.
[4] Joachims T, Finley T, Yu C N J. Cutting-plane training of structural SVMs[J]. Machine Learning, 2009, 77(1): 27-59.[5] Keerthi S S, Lin C J. Asymptotic behaviors of support vector machines with Gaussian kernel[J]. Neural computation, 2003, 15(7): 1667-1689.
[6] Lin, Hsuan-Tien, and Chih-Jen Lin. ?A study on sigmoid kernels for SVM and the training of non-PSD kernels by SMO-type methods.? submitted to Neural Computation (2003): 1-32.
[7] Suykens J A K, Vandewalle J. Least squares support vector machine classifiers[J]. Neural processing letters, 1999, 9(3): 293-300.
