基于马尔可夫链预测模型的昆明市房价预测分析オ

韦光兰等

[摘要]近年来，政府出台了一系列楼市调控政策，加之央行连续两次降息，必然对楼市产生一定影响。基于此，本文在统计昆明市近四年来住宅月度销售单价的基础上，分析房价的动态变化过程，并以马尔可夫链为预测模型，采用数理统计的计算方法，预测了昆明近期房价走势，以期为近期购房消费者提供可借鉴的参考。

[关键词]马尔可夫链；预测；房价

[DOI]1013939/jcnkizgsc201521.086

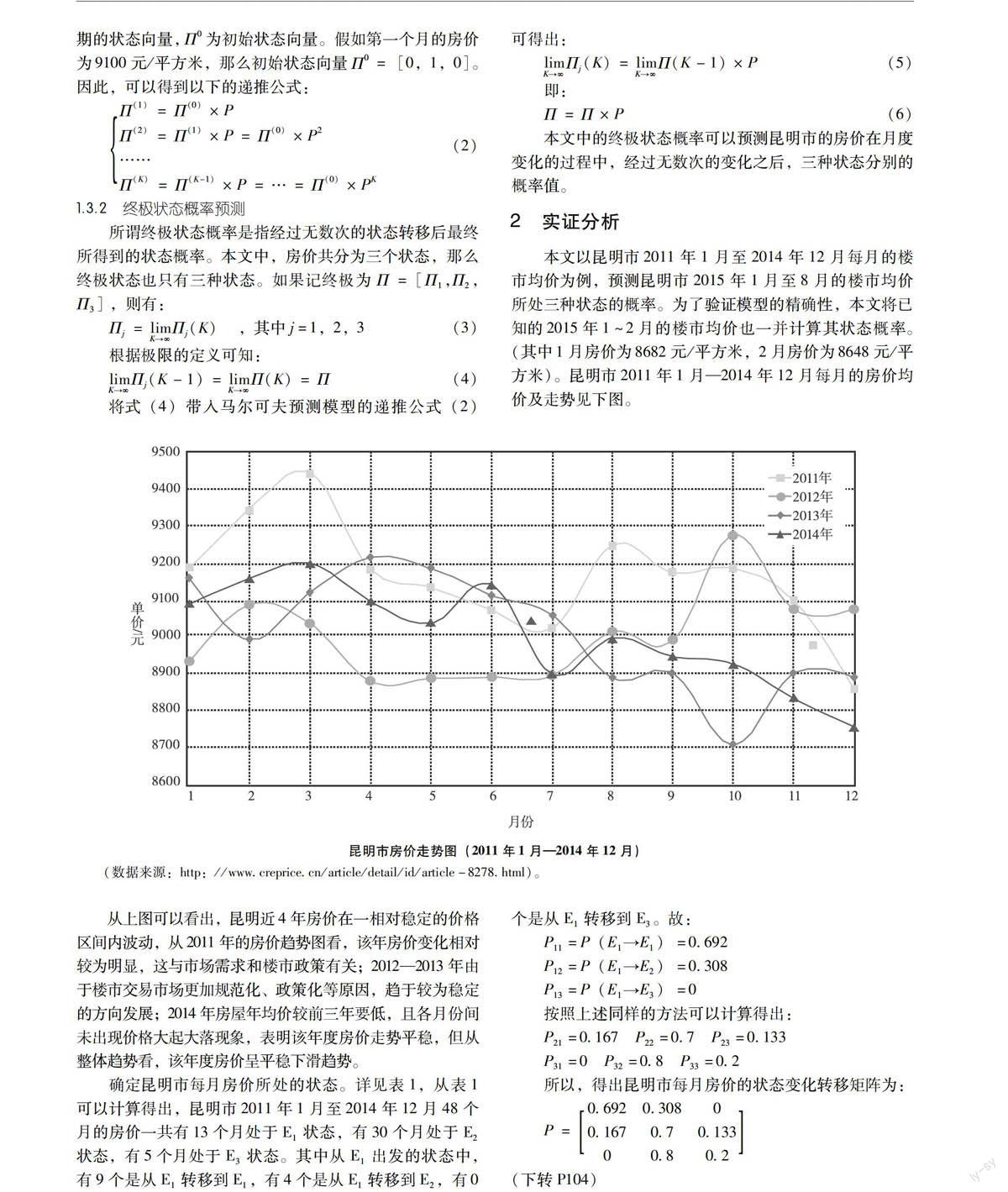
自2011年国务院常务会议推出“新国八条”以来，在房地产市场引起了一系列的相关反应，消费者持币待购，销售遇阻，昆明楼市表现持续低迷。2014年2月，公积金新规出台，调整公积金贷款首付额度；8月，限购取消；9月，限贷松绑；11月，央行降息。与此同时，在《2014—2015年度中国35城房地产短周期投资风险度排名》报告中昆明房地产短周期投资风险全国排名第三。大量存量房的存在，导致昆明各大楼盘降声肆起，营销的方式更是层出不穷，有南悦城2万抵5万元的宣传；名旺角7899元/平方米，比同区域楼盘价格低25%的宣传；俊发房交会7盘限量巨惠的广告；东盟森林4488元/平方米、中豪优活城首付仅需2.99万元的广告和宣传；奥宸1万减5万元、海伦堡6666元/平方米特价房、恒大雅苑88折、人民路1号20套特价房7折、兆丰六千城买房100%奖车等宣传。

但面对现在的市场环境，购房者会产生怎样的购房心理？一方面各大楼盘相继降价的信息，导致消费者购房信心急剧下滑，甚至流言四起：“楼市要崩盘了，房子不能买了”；另一方面部分专业人士认为，国家近期出台的取消限购、限贷及降息政策，大量的刚性需求及改善性需求将会释放出来，此时昆明的房价已经跌入低谷，从2015年开始，将会有回暖的可能，而此时是最佳的购房时机。

1马尔可夫预测的原理及步骤

马尔可夫（Markov）法是以俄国数学家马尔可夫（AAMarkov）名字命名的一种方法，它将时间序列看作一个随机过程，通过对事物不同状态的初步概率和状态之间转移概率的研究，确定状态变化的趋势，以预测事物的未来。马尔可夫理论指出：“系统达到每一状态的概率仅与近期状态有关，在一定时期后马尔可夫过程逐渐趋于稳定状态而与原始条件无关”的这一特性称为“无后效性”[1]。即：事物的第n次试验结果仅取决于第（m-1）次试验结果，第（n-1）次试验结果仅取决于第（n-2）次试验结果，以此类推[2]。这里所说的状态，就是指某一事件在某个时刻出现的某种结果。比如，在商品销售预测中，有“畅销”“一般”“滞销”等状态。再比如在房价中，可以划分“上升”“持平”“下降”三个状态。房价由三种状态中的一种状态到另一种状态的变化称为状态转移。本文将利用昆明市2011年1月至2014年年底48个月的商品住宅均价为基础，采用数理统计的方法计算出房价的马尔可夫链状态转移概率。

由表2可以看出，2015年1月和2月房价处于E1状态的概率最大，概率分别为0692和0530，即价格为8600元/平方米～8900元/平方米，而实际房价分别为8682元/平方米、8648元/平方米，说明预测的概率结果与实际相符。从6月开始，房价逐渐趋于E2状态，即持平状态。

由公式（3）～（5）可以计算出昆明市的房价经过数月之后所处的概率值。分别为：E1=0318，E2=0585，E3=0097，即：E2>E1>E3。这说明了昆明市的房价经过数月变化之后，房价趋于持平的概率最大，占585%的可能性，其次房价趋于下降的概率占31.8%，上涨的概率占97%。即昆明在未来一段时间的房价涨价的可能性不大，很大可能会一直处于持平的状态。

3结语

本文在在统计分析昆明市近4年来房价变化的基础上，运用马尔可夫链预测方法，得到昆明市未来房价发展趋势的结论是：从目前到2015年5月，房价下跌的可能性较大，但是从下半年开始房价将会略有回暖，处于平稳状态，未来一段时间，如果没有大的政策出台，昆明市的房价稳定状态将继续保持，说明政府自2011年以来出台的调控政策有一定的成效，未来房地产将会进入到回归秩序的时期，到一定时期后，趋于成熟发展。对于还没有买房的消费者来说，近期买房是合理的。最后应该指出本文运用马尔科夫预测模型对昆明市房价进行预测，预测结果有一定的准确性。但是运用该方法预测出的结果只是表明昆明市房价最终趋向于某个状态，而不是绝对处于该种状态。没有任何一种预测方法可以准确的计算出房价。

参考文献：

[1]杜纲管理数学基础——理论与应用[M].天津：天津大学出版社，2003.

[2]严伟，钱育渝马尔科夫预测在房地产市场营销中的应用研究[J].重庆建筑大学学报，2004，26（2）：110-115

[3]张宗国马尔可夫链预测方法及其应用研究[D].南京：河海大学，2005

[4]贺福利，胡勇，陈淳用灰色马尔科夫链预测模型对我国粮食产量的预测[J].数学的实践与认识，2003，33（12）：45-47