浅论数形结合思想在初中函数教学中的渗透

钟世辉

[摘要]“数形结合”作为数学的一种重要思想，是提高学生数学能力和数学素养的重要途径.主要从情境创设、图像信息获取和前后知识联系几个方面进行数形结合思想的渗透，分析如何指导学生用简洁、直观的方法解决函数问题.

[关键词]初中数学函数教学数形结合

[中图分类号]G633.6[文献标识码]A[文章编号]16746058（2015）110027

笔者结合初中数学函数部分的教学经验及中考函数题发现，在函数教学中渗透数形结合思想是十分必要的.数形结合思想能将函数的复杂问题简单化，将抽象的问题具体化，从而化难为易，帮助学生加强对函数知识的理解.同时，在函数教学中渗透数形结合思想，还可以培养学生的思维能力.下面简单谈谈如何在初中函数教学中渗透数形结合思想.

一、让学生在情境中体会数形结合思想

数形结合思想的基本内容是把抽象的数学概念和形象的图形结合起来，也就是将抽象思维与形象思维相结合，通过问题提供的条件构建出相应的数学图形或者模型，以达到“以形助数”“以数辅形”的目的.在函数概念的教学中，教师可以通过创设一定的情境，激发学生的学习兴趣，让学生体会数形结合思想.

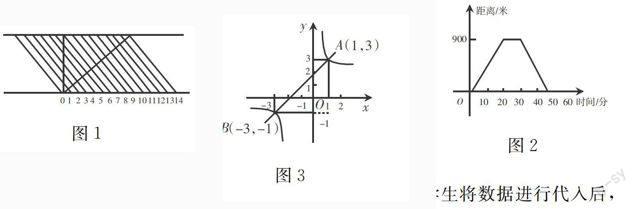
比如，教学“一次函数”时，教师可以给学生讲述有关的故事：“有一位数学家提出了一个他认为很难的问题，即每天中午都有一艘船从A地开往B地，而每天的同一时刻也都有一艘船从B地开往A地，途中所花的时间都是七天.假设它们在同一条直线上匀速前进，那么今天从A地出发的船会在路上迎面碰到几艘船呢？这个问题确实令许多人无从下手，最后，有一位数学家画出了一个简单的图形解决了这个问题.”听完故事，学生会感到困惑：究竟是哪位数学家画出了什么图形解决了这个问题？此时，教师可以指导学生画出图1.图1由图1可知，从左下角到右上角的线段和图中的平行线段有15个交点，因而会和迎面开来的15艘轮船相遇.

二、让学生通过画图感悟数形结合思想

在函数教学中，教师也可以根据课堂内容设计相关的教学活动，将数形结合思想渗透于其中，从而培养学生的数形结合意识.

教师可以让学生通过已知条件画图，并在这一过程中感悟数形结合思想，同时，教师也可以直接让学生进行图像解读.比如，教学“一次函数的表达式”时，图2教师可向学生展示物体移动的距离随时间的变化而变化的图像（如图2），让学生根据图2求函数式.一开始，学生无法判断这是什么性质的函数，在学生一筹莫展时，教师给予提示：可以将其分解，分成三段函数.于是学生慢慢从图像中获得了相应的信息：前二十分钟内，距离随时间增长而变大，一共是移动了900米；中间的十五分钟距离不变；而后十五分钟里，距离随时间增长而变小，最后变为0.因此可以判定这是三个一次函数构成的分段函数.根据之前学过的知识，学生将数据进行代入后，求出了相应的函数式.

三、联系前后知识，引导学生掌握数形结合思想的内涵

函数教学不是孤立的，它与其他数学知识之间存在密切的联系，如函数与方程、函数与几何图形等.教师在教学中应当注意加以引导，适当地举例和联系旧知识，让学生将数与形结合起来，从而在巧妙地解决问题的同时，掌握数形结合思想的内涵，明白数形结合对函数学习的重要性.

【例1】存在一次函数y=x+2与反比例函数g=3x相交于点A（1，3）、B（-3，-1），请问x为何值时，y>g；x为何值时，yg>0？

图3解析：若直接联立两个函数式，可得出：x+2>3x.面对这样的式子，大部分学生不知如何下手.这时教师可以提示学生用图像来解答，如图3.

从图像上可以观察出，如果y>g，则y的图像应该在g的图像上方，那么只要找出y图像位于g图像上方的部分x的取值范围即可.通过观察，可得出当x>1或-3g.而如果yg>0，则y、g必须同正或同负，根据图像可知，只要找出两个函数图像同在x轴上方的部分或同在x轴下方的部分就可以了，由此可知，x>0或x<-2.

总之，在数学中“数”和“形”是两大重点，尤其在函数教学中，教师应运用各种教学手段渗透数形结合思想，以提高学生的数学素养和思维能力.

（责任编辑钟伟芳）