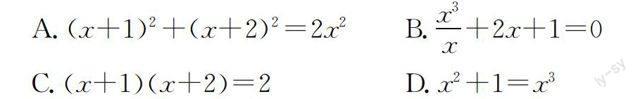初中数学概念教学有效策略探微
2015-05-30杜少锋
杜少锋
[摘要]数学概念既是数学思维的起点,又是学生数学能力培养的重要组成部分.在素质教育的背景下,如何实现初中数学概念有效教学成为数学教师的当务之急.
[关键词]初中数学概念教学有效策略
[中图分类号]G633.6[文献标识码]A[文章编号]16746058(2015)110022
数学概念的教学贯穿于数学教学的始终,对初中生数学思维和数学素养的培养有着重要的作用.数学概念的一般组成包括概念定义、定理应用、数学推论等.要想深入理解数学概念,需要对其中的字、词、句以及注解仔细剖析.在长期的数学概念教学实践中,我总结出了以下的一些教学策略.
一、数学概念情境教学
在传统的数学概念教学中,教师往往照本宣科,只是单纯地复述教材上的数学概念.由于数学概念的形成是从一般形象到普遍抽象的过程,要想帮助学生实现清晰的概念学习思路,教师必须创设相应的概念教学情境,还原概念的形成过程.例如,在“二维平面坐标系”时,我利用电影院座位布置的情境进行教学.在电影票上,常常会写明几排几座,对于平面坐标系的构建同样如此.利用横坐标和纵坐标的数值,我们便可以在坐标系中确定这一点在平面内的位置.此外,在电影票上常常还会标注几号厅,如此一来,便可以拓展到三维坐标系的教学.学生不知不觉中进入了数学概念的学习.但是,值得注意的是,生活案例并不等于数学概念本身,教师在进行概念情境教学时必须注意其中的根本属性.比如,对“三维坐标系”的概念教学,要是单一对电影院位置布置的情境进行教学,学生难以将平面与空间相联系.对此,教师必须强调其中的维度关系,利用空间几何图形来辅助三维坐标系的概念教学.在进行其他数学概念的情境教学时,教师同样需要注意所选取教学情境的针对性和实用性,切忌生搬硬套.我认为,存在于学生身边的、富含生活气息的数学情境不仅可以实现数学知识的教学,同时也有助于营造课堂和谐的氛围.
二、数学概念类比教学
数学概念的教学是一个系统性的教学,在很多时候,数学概念之间是环环相扣的.要是学生不理解数学方程的概念,自然也就不理解数学函数的概念.对此,教师需要将数学概念进行分类总结,进行类比式教学,帮助学生尽早建立数学概念知识网络.例如,在进行初中数学有理数和无理数的教学时,教师不妨利用π与3.1415927的区别进行概念类比教学.前者是无限不循环小数,后者是有限小数.自然前者就是无理数,后者为有理数.利用这样的类比教学,学生在正反案例的比较中也就能够获得较为深刻的理解.在数学概念知识网络的构建中,教师可以为学生进行相关专题的概念教学.在进行复习和预习时,利用网络图将相关概念和类似概念进行罗列和类比,帮助学生分清各类概念的适用范围,发现其中所隐藏的陷阱,从而引发学生对数学概念的思考.例如,在进行初中数学“函数”的概念教学时,从平面直角坐标系、变量与函数的概念教学入手,再依次展开正比例函数、一次函数、反比例函数、二次函数的概念教学.如此循序渐进,依次铺开,必然可以帮助学生有效掌握数学概念.概念类比教学最有效的时间段是在复习阶段,利用类比式数学概念教学,能帮助学生有效理清各个章节的概念学习思路,有利于学生构建缜密的思维体系.
三、数学概念应用教学
与其让教师反复地讲解,我们不妨利用数学习题来实施概念教学.数学概念的深刻理解是提高学生解题能力的关键.这样,学生才能在解题过程中实现对数学概念的延伸和应用.对此,在数学概念的教学中,我在教学伊始和概念复习阶段总会选取对应的概念应用类数学题,帮助学生加深对概念的理解.例如,在进行数学“函数”概念的教学时,我选取了如下的训练题.
【例题】下列方程中属于一元二次方程的是().
A.(x+1)2+(x+2)2=2x2B.x3x+2x+1=0
C.(x+1)(x+2)=2D.x2+1=x3
分析:显然,化简之后,该题的答案是选项C.要想做对该题,必须对一元二次方程的概念做到深刻理解.一元即是对应只有一个未知量;二次即是指方程中的最高项数为二次;最后该表达式必须是方程的形式.只有满足以上三点的选项才是正确选项.在这样的概念应用教学过程中,学生对数学函数的定义必然会有更加深刻的认识.同时,利用不同选项之间的区别性,学生对因式分解、方程化简等数学知识也产生了更加深刻的认识.教师需要针对数学概念教学的不同阶段选择难度合适的教学.在预习课的概念教学时,必须选取偏向于基础性概念应用的习题;在复习教学时,教师则应选取偏向于概念应用类型的训练题,帮助学生实现对数学概念的应用和拓展延伸.
总之,初中数学概念教学是一个循序渐进和依次深入的过程,要想实现有效的数学概念教学,教师必须敢于创新、勇于采取新方法.数学概念作为初中数学教学的基础,唯有帮助学生深刻认识数学概念的内涵,在实践应用中总结提炼,才能不断实现初中数学概念教学的有效性.
(责任编辑黄桂坚)