寻找四色定理和完整四色地图的制作

方和生　方祖旺

【摘要】由等边三角形组合成正六边形，又从六边形变换成长方形，得出一个二面完整的四色体面地图.

【关键词】 六边形平面地图；长方形体面地图；长方形平面地图

自从美国数学家阿佩尔和哈肯同时用两台计算机用了1200个小时，得出了证明，权威也认可了，但人们还没欣赏到他的作品，他的结论一定是一种及限，不能实践证明，比如：在20厘米的图纸上画一个960个国家的四色地图，在图纸上就完成不了，只能用计算机证明，而我有一种新方法献给大家，发此论文，大家参考.

一、四色定理的变换与修改

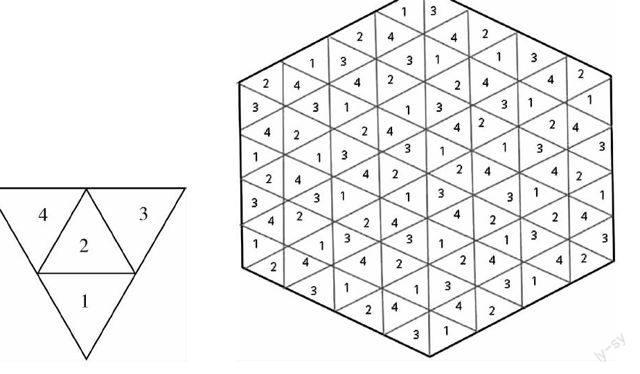
定理一： 画一个等边三角形的四色小区 （见图1）

把六个小区组成一个六边形，再把各小区向外扩大二格、四格、六格、八格、十格等等.在任一个四色小区内任意填上1，2，3，4代表四色，再以对宫的格式填完整个表格 （见图2）.

定理二制作完整的体面四色地图

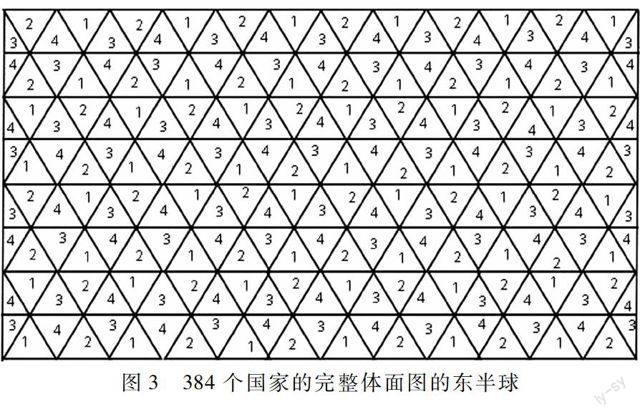
在任一个按定理画的六边形表格中，只要每个外边格数是双，都可以化为完整的四色体面地图，如：二格、四格、六格、八格、十格等等很多很多，把六边形的两个相对的边向背后摘过去合并，又把两头的尖角向背后摘去合并，恰好成为一个长方形的二面四色地图，也是体面四色地图.可增减长边上的格式，能得出很多很多不国家数的完整四色地圆.（见图3）

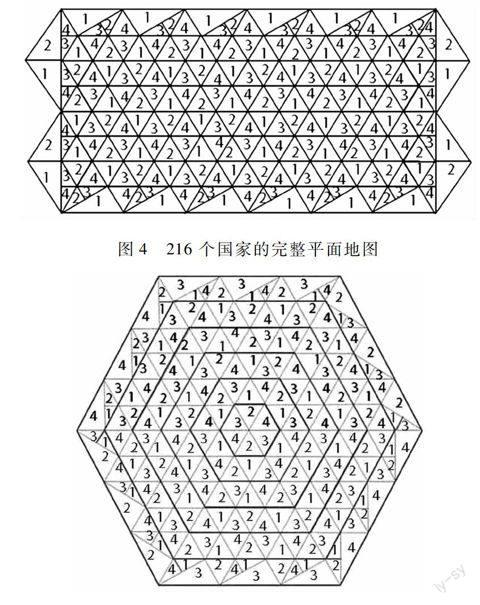
定理三制作完整的平面四色地图

在任一个边格是双的六边形和由六边形变化出来的长方形表格中，只要稍一修改外围格式，就能成为完整的平面四色地图，任意增减长边上的格式，也可修改成完整的四色地图.（见图4和图5）二、猜想阿佩尔的四色定理

以32个国家的地图证明：画一个圆，再画上直径，把直径八等分，各等分点与A，B连接，在上半圆内填上1，2，3，4，1，2，3，4：下半圆填上3，4，1，2，3，4，1，2，此图为32国的东半球，这种方法国数少可以人工证明，国数一多进入极限了，只能计算机证明，如强行人工证明，线条会画满图纸，肉眼就分不清楚了.（见图6）

结论：一合二变三修改，平面体面都出来，四色完整地图摆，中国文化走世界.欢迎评，欢迎论，接受挑战和指正，理论实践有过程，希望权威来确认.